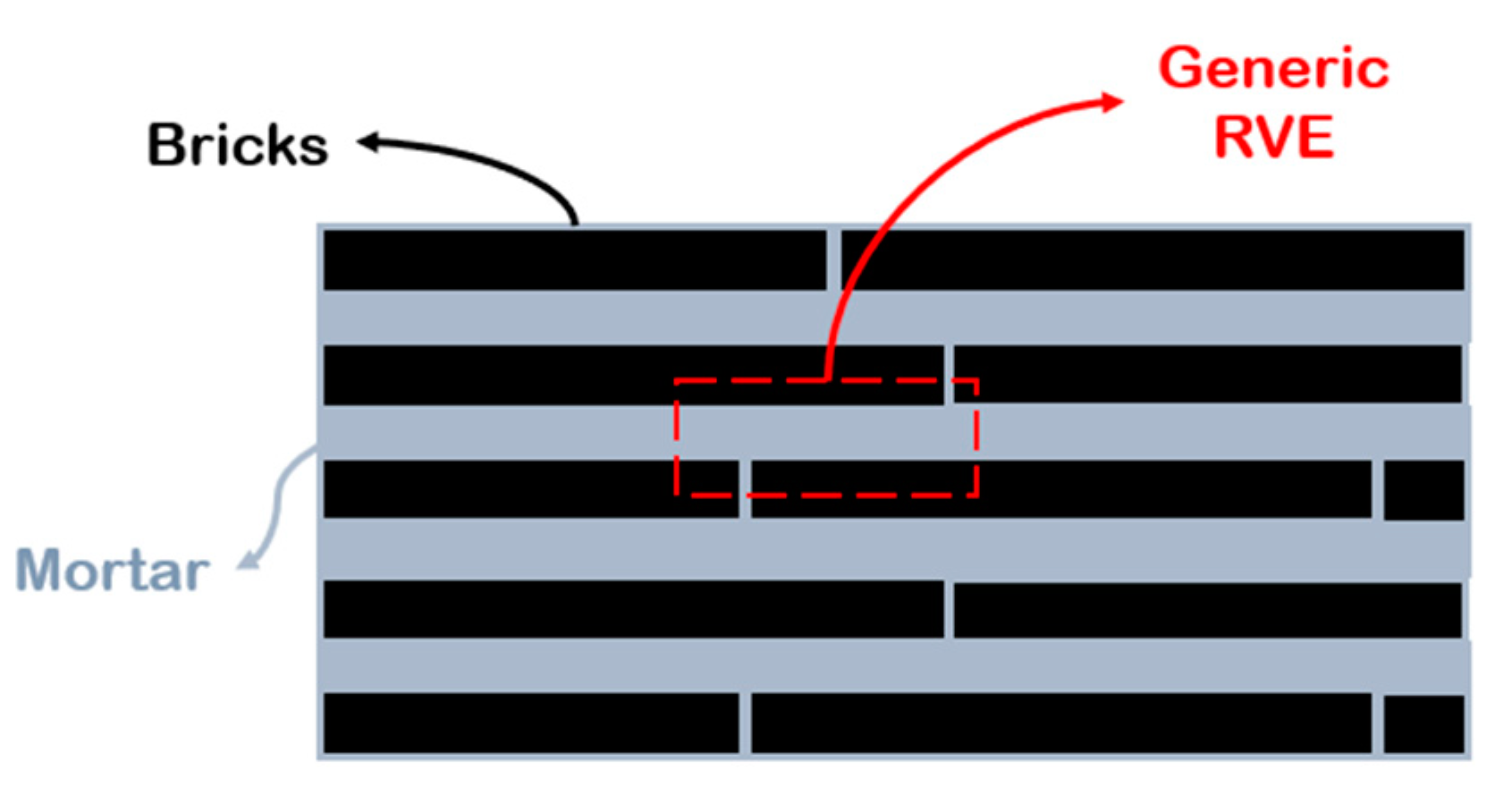
Among all biomimetic materials, nacre has drawn great attention from the scientific community, thanks to superior levels of strength and toughness and its brick-and-mortar (B&M) architecture. However, achieving the desired performances is challenging since the mechanical response of the material is influenced by many factors, such as the filler content, the matrix molecular mobility and the compatibility between the two phases. Most importantly, the properties of a macroscopic bulk material strongly depend on the interaction at atomic levels and on their synergetic effect. In particular, the formation of highly-ordered brick-and-mortar structures depends on the interaction forces between the two phases. Consequently, poor mechanical performances of the material are associated with interface issues and low stress transfer from the matrix to the nanoparticles. Therefore, improvement of the interface at the chemical level enhances the mechanical response of the material.
- GNP
- nanolaminates
- brick-and-mortar
1. Introduction
1.1. Mimicking Nature: Nacre-Inspired Materials
1.2. Engineering Materials Based on 2D Nanoparticles
| Filler | Matrix Type | Composite Mechanical Behaviour | Composite Conductivities |
|---|---|---|---|
| Graphitic (GO, RGO, GNP, Pyrolytic Graphite…) | Brittle | Pseudo-elastic | Electrically Conductive in plane High ratio in plane/trough thickness thermal conductivity |
| Ductile | Plastic | ||
| Ceramic (MTM, Alumina, Silica…) | Brittle | Pseudo-elastic | Isolating |
| Ductile | Plastic |
Several attempts have been made to mimic and design artificial nacre. For this purpose, different materials have been employed as bricks and mortar. The most employed nanoparticles used as reinforcement are listed in Table 2, and a comparison in terms of costs, mechanical properties and thermal and electrical conductivities is presented.
| Particle | Costs | Geometry | Elastic Modulus | In Plane—Therm. Cond. | Elec. Cond. |
|---|---|---|---|---|---|
| Graphene | EUR 200–300 per flake | Monolayer | 1 TPa [6] |
5000 W/mK [6] |
107–108 S/m [6] |
| GO | 2–5 layers 48 EUR/g |
2–5 layer BET 420 m2/g |
250 GPa [7] |
72 W/mK with an oxidation degree of 0.35 [8] |
270 S/m [9] |
| RGO | 2–5 layers 68 EUR/g |
2–5 layer BET 1562 m2/g |
250–350 GPa [10] |
670 W/mK with an oxidation degree of 0.05 [8] |
4480 S/m [11] |
| GNP | 6–10 EUR/g | >10 layer BET 30 m2/g |
25–40 GPa [12] |
300–470 W/mK [5] |
2 × 106 S/m [13] |
| MTM | <1 EUR/g | BET 750 m2 very high (nm × µm) aspect ratio |
207 GPa [14] |
16 W/m [15] |
25 to 100 mS/m [15] |
1.3. Technologies Enabling Industry Applications
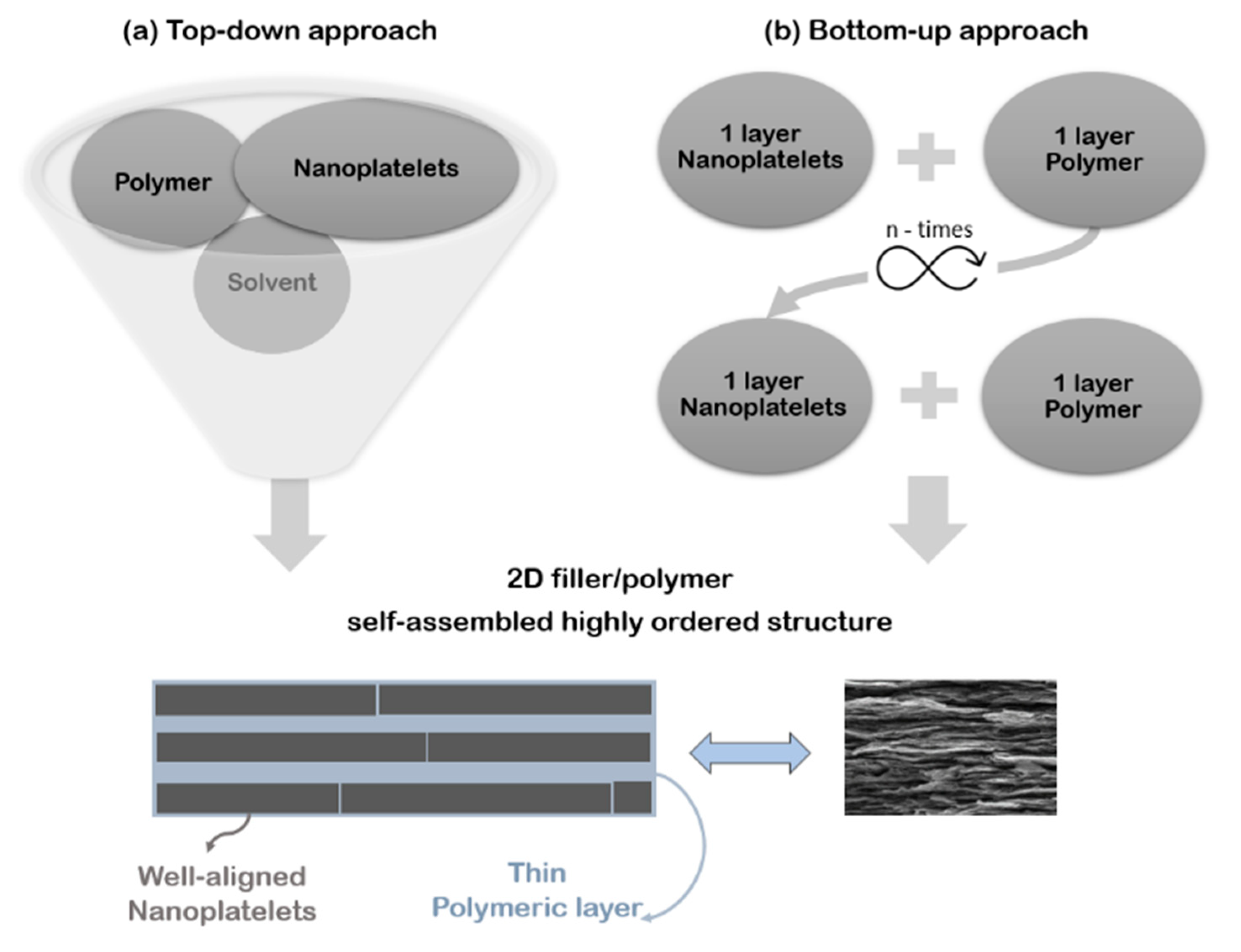
2. Mechanical Performances
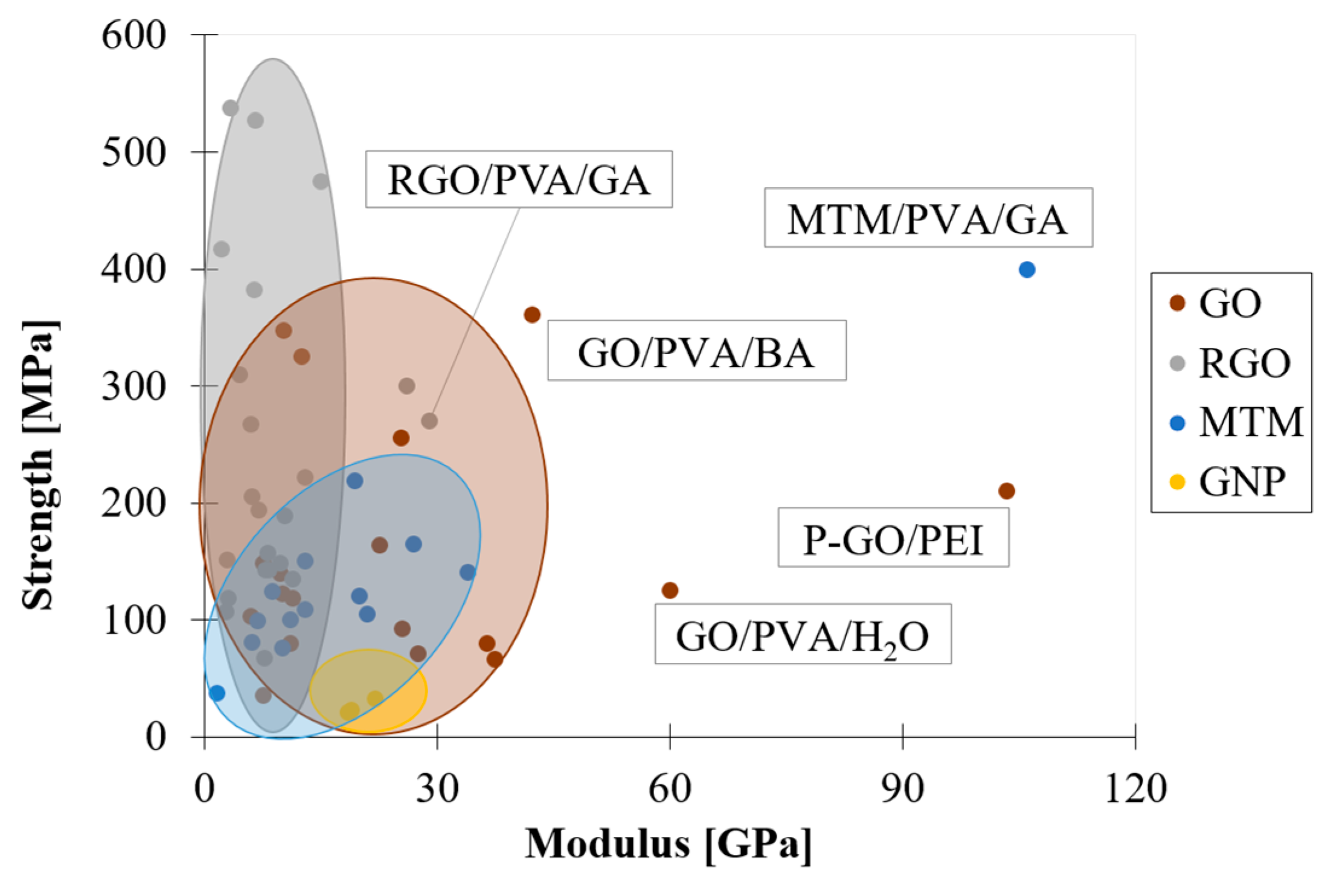
2.1. Influence of Filler Content
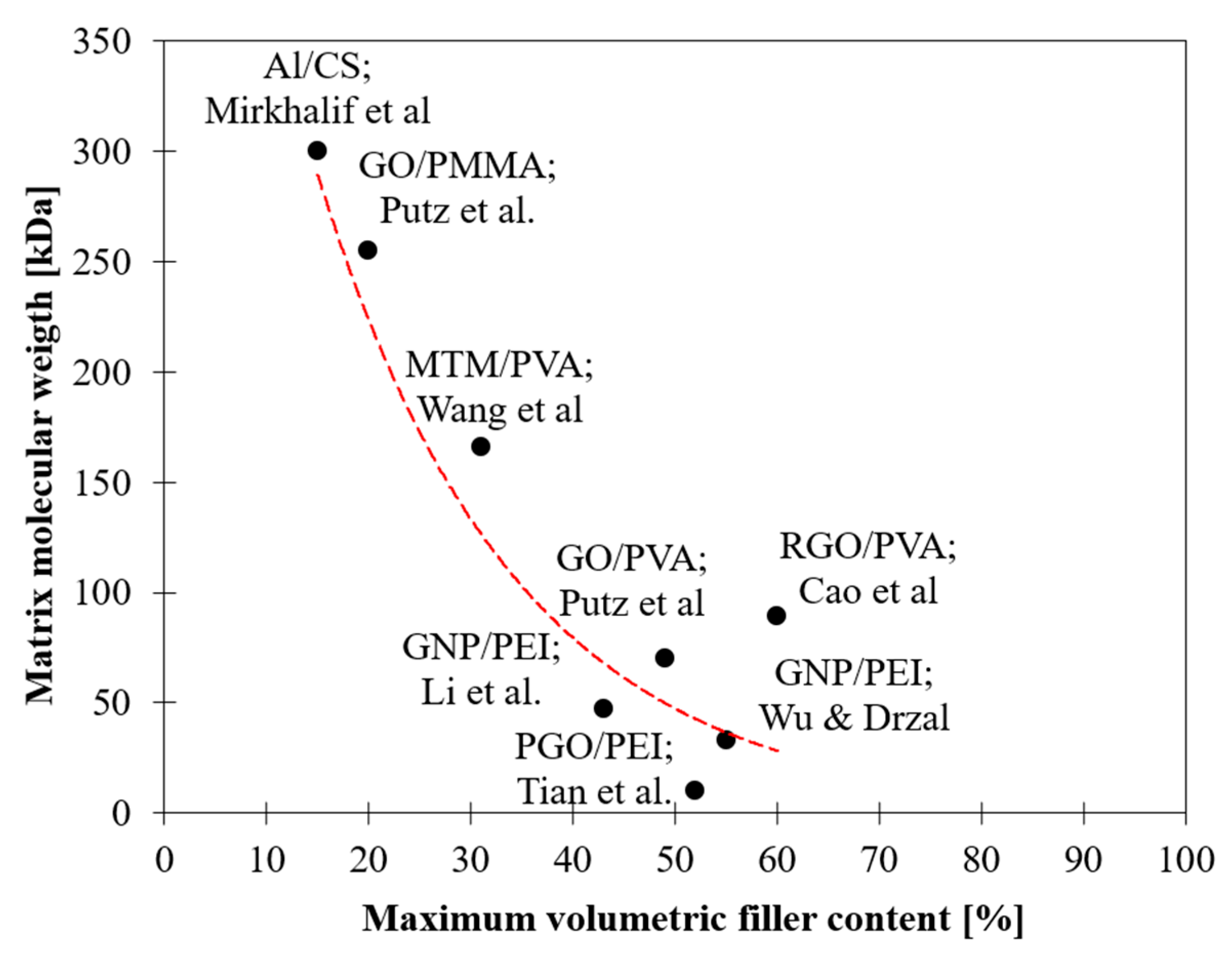
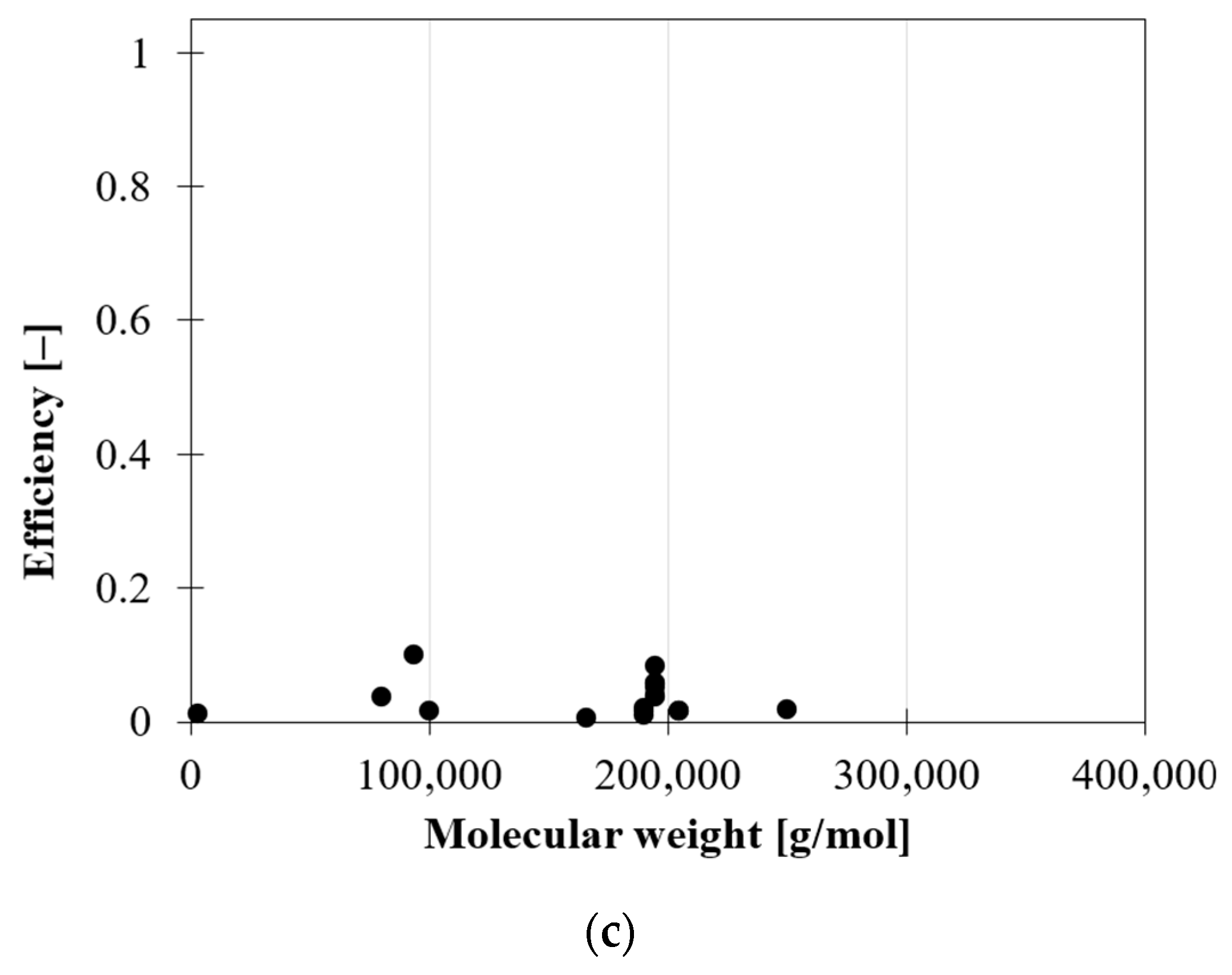
2.2. Influence of Matrix—Effect of Matrix Molecular Weight
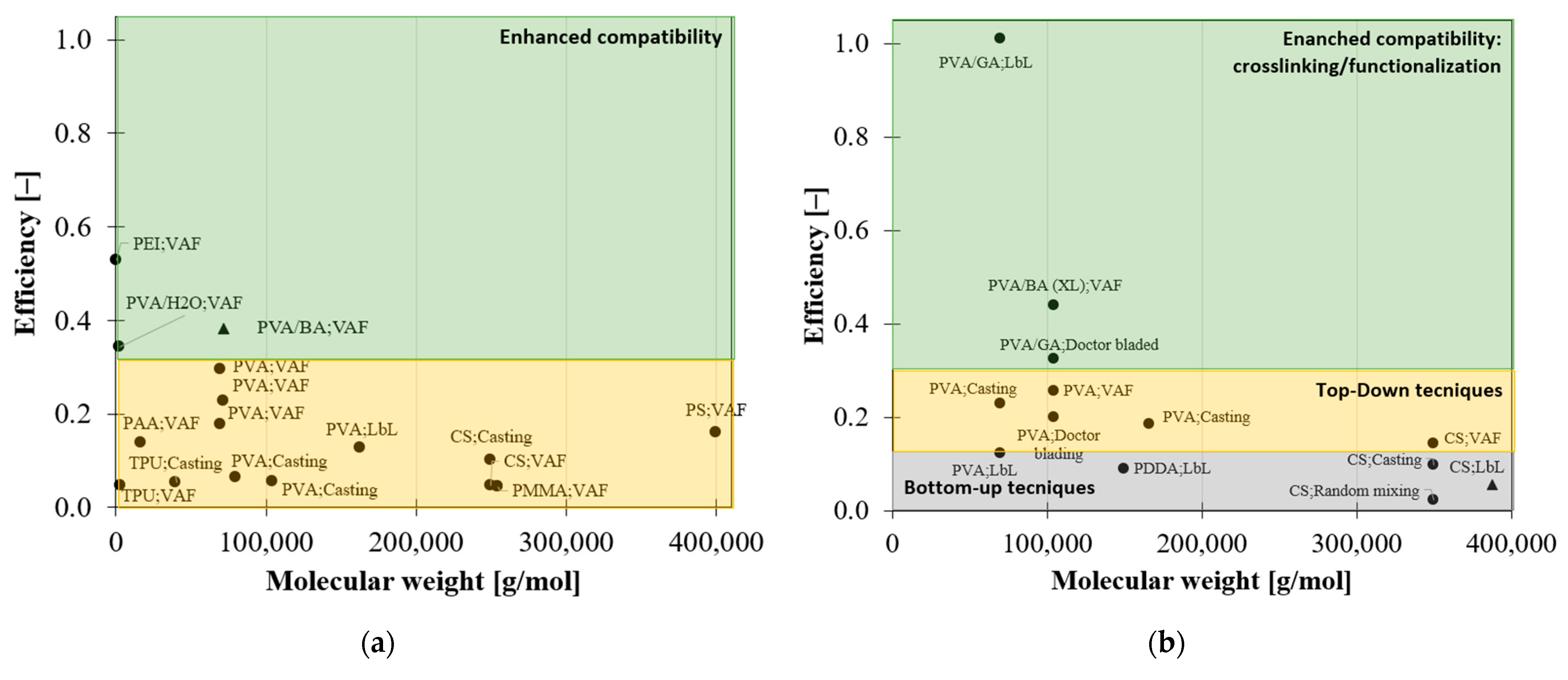
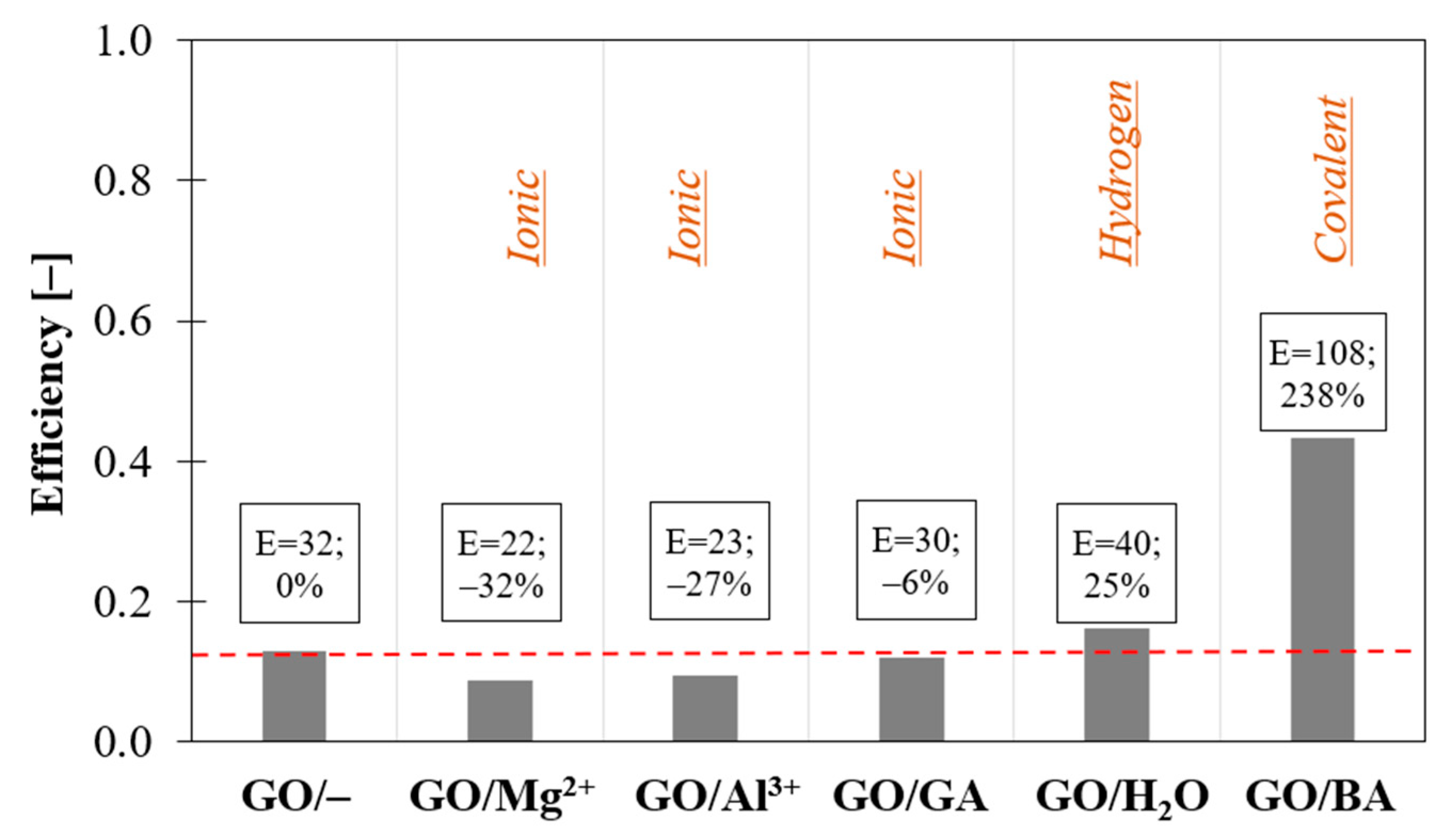
2.3. Filler/Matrix Compatibility—Chemical Bonding
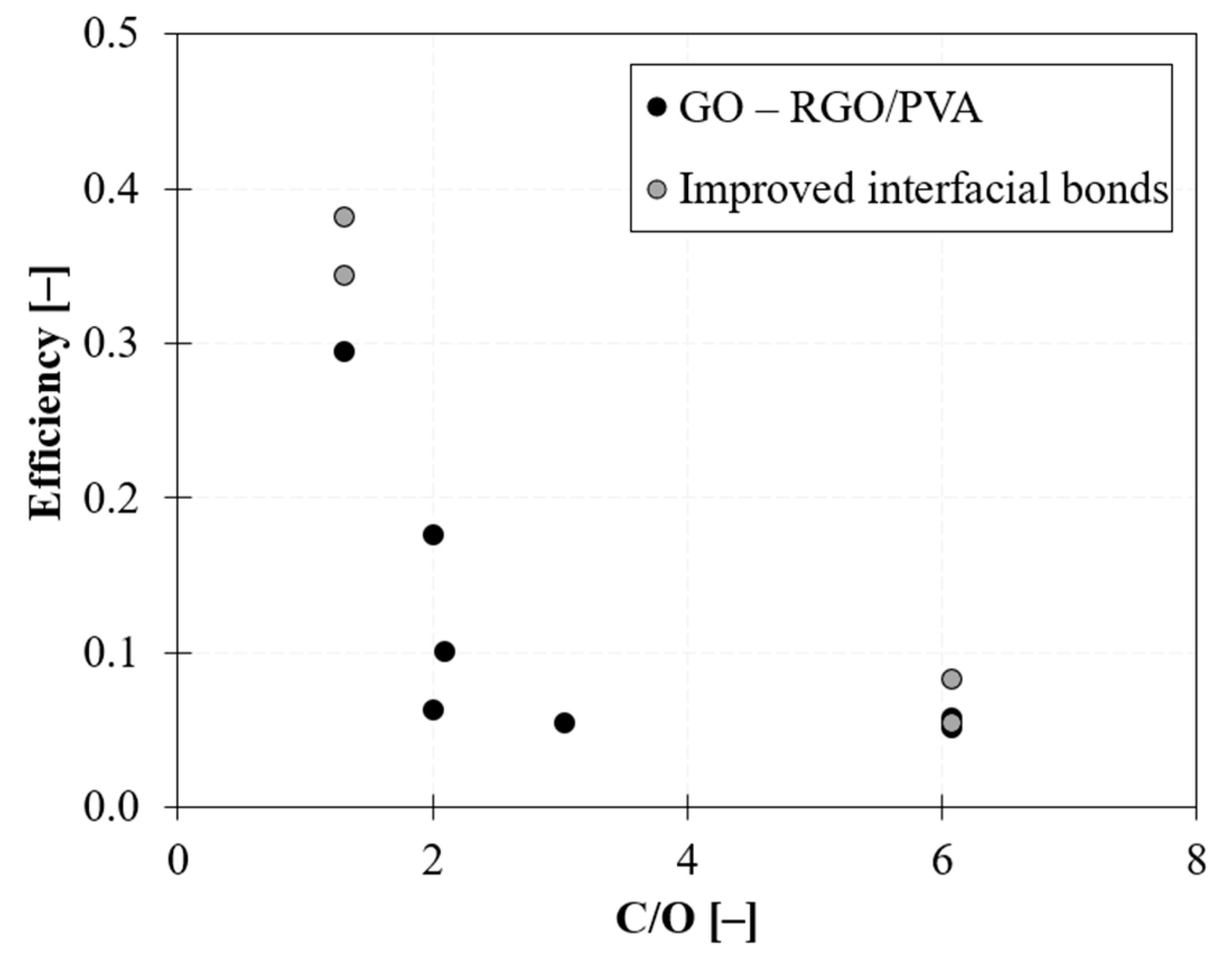
2.4. Interfacial Shear Strength
3. Analytical Models for the Prediction of Mechanical Properties
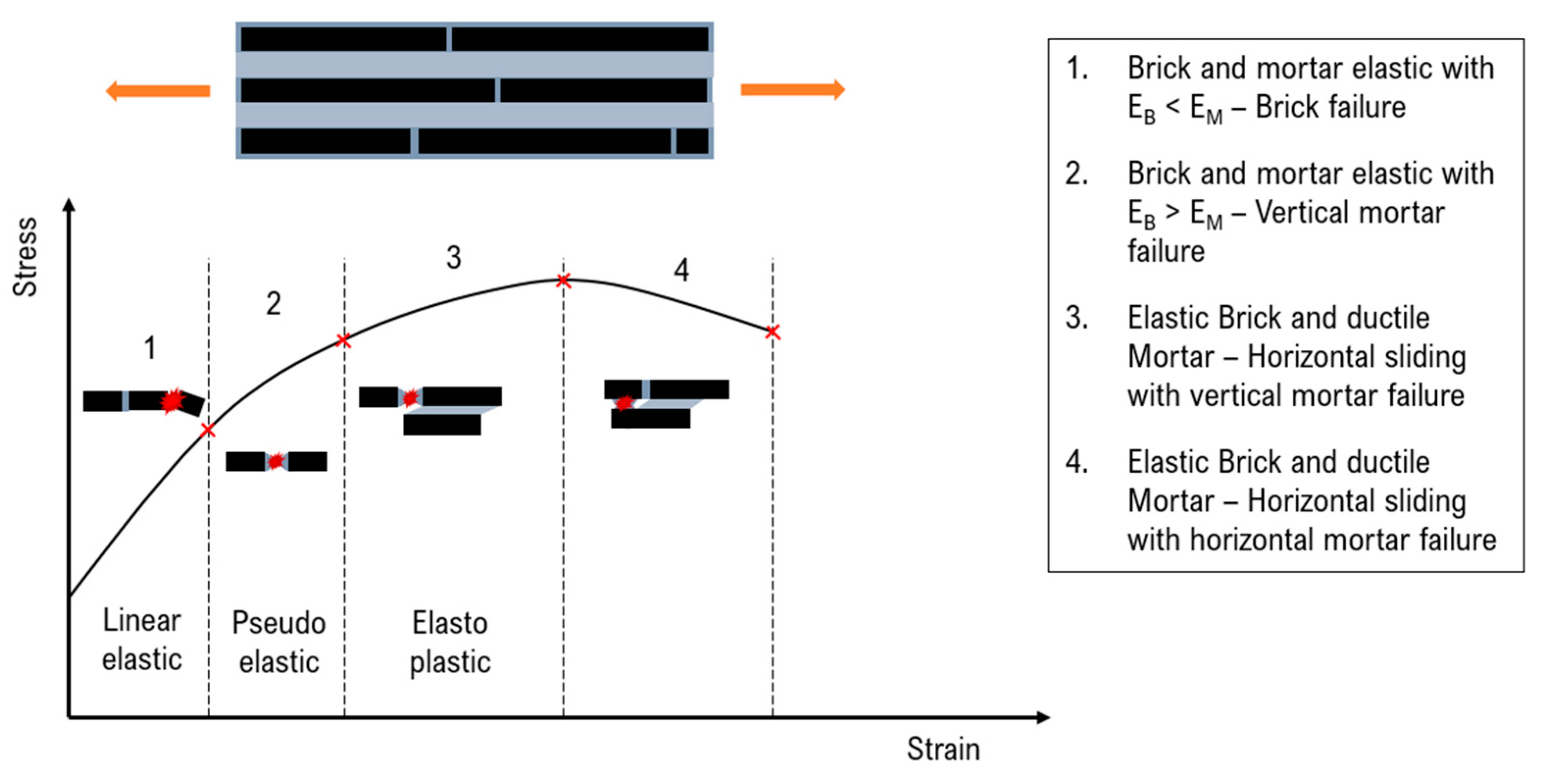
4. Conclusions
Although composites with brick-and-mortar architecture are promising from a theoretical point of view, in reality, it is challenging to achieve the desired mechanical performances. The target is to assemble 2D nanoparticles in order to achieve a macroscopical material able to reproduce the unique properties of the 2D nanoparticle:
vf →1 ↔ Ec ≈ E2D particle
This condition can be achieved when the matrix arranges as a continuous nanometric film on the nanoplatelets’ surface and the complete stress transfer at the interface is guaranteed, according to the shear lag theory. However, the mechanical response of the material is influenced by several factors: volumetric filler content, matrix molecular mobility and compatibility between the two phases. Thus, the efficiency of reinforcement:
- Drops at high filler content. Starting from a critical volumetric fraction, the elastic modulus B&M composites deviate from the expected behaviour dictated by the rule of mixture due to the partial coverage of the nanoplatelets at the nanoscopic level.
- Decreases as the molecular weight increases.The higher the molecular mobility of the polymer and the capacity to intercalate between nanoplatelets, the better the stress transfer at the interface.
- Improves when a high interfacial attraction between nanoparticles and the surrounding matrix is guaranteed. Strong chemical bonding and molecular interactions between nanoparticles and the polymer ensure self-assemblies with a tendency toward forming intercalated morphologies, with a stable layer of polymer between flakes.
This entry is adapted from the peer-reviewed paper 10.3390/nano12081359
References
- Sun, J.; Bhushan, B. Hierarchical Structure and Mechanical Properties of Nacre: A Review. RSC Adv. 2012, 2, 7617.
- Espinosa, H.D.; Rim, J.E.; Barthelat, F.; Buehler, M.J.; Espinosa, H.D. Merger of Structure and Material in Nacre and Bone-Perspectives on de Novo Biomimetic Materials. Prog. Mater. Sci. 2009, 54, 1059–1100.
- Niebel, T.P.; Bouville, F.; Kokkinis, D.; Studart, A.R. Journal of the Mechanics and Physics of Solids Role of the Polymer Phase in the Mechanics of Nacre-like Composites. J. Mech. Phys. Solids 2016, 96, 133–146.
- Balandin, A.A. Thermal Properties of Graphene and Nanostructured Carbon Materials. Nat. Mater. 2011, 10, 569–581.
- Cilento, F.; Martone, A.; Cristiano, F.; Fina, A.; Giordano, M. Effect of Matrix Content on Mechanical and Thermal Properties of High Graphene Content Composites. MATEC Web Conf. 2019, 303, 01002.
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388.
- Suk, J.W.; Piner, R.D.; An, J.; Ruoff, R.S. Mechanical Properties of Monolayer Graphene Oxide. ACS Nano 2010, 4, 6557–6564.
- Chen, J.; Li, L. Thermal Conductivity of Graphene Oxide: A Molecular Dynamics Study. JETP Lett. 2020, 112, 117–121.
- Chen, H.; Müller, M.B.; Gilmore, K.J.; Wallace, G.G.; Li, D. Mechanically Strong, Electrically Conductive, and Biocompatible Graphene Paper. Adv. Mater. 2008, 20, 3557–3561.
- Liu, L.; Zhang, J.; Zhao, J.; Liu, F. Mechanical Properties of Graphene Oxides. Nanoscale 2012, 4, 5910–5916.
- Cui, W.; Li, M.; Liu, J.; Wang, B.; Zhang, C.; Yiang, L.; Cheng, Q. A Strong Integrated Strength and Toughness Artificial Nacre Based on Dopamine Cross-Linked Graphene Oxide. ACS Nano 2014, 8, 9511–9517.
- Cost, J.R.; Janowski, K.R.; Rossi, R.C. Elastic Properties of Isotropic Graphite. Philos. Mag. 1968, 17, 851–854.
- Wu, H.; Drzal, L.T. Graphene Nanoplatelet Paper as a Light-Weight Composite with Excellent Electrical and Thermal Conductivity and Good Gas Barrier Properties. Carbon N. Y. 2012, 50, 1135–1145.
- Rafiee, R.; Shahzadi, R. Mechanical Properties of Nanoclay and Nanoclay Reinforced Polymers: A Review. Polym. Compos. 2019, 40, 431–445.
- Uddin, F. Montmorillonite: An Introduction to Properties and Utilization. In Current Topics in the Utilization of Clay in Industrial and Medical Applications; Zoveidavianpoor, M., Ed.; IntechOpen: London, UK, 2018; pp. 3–24.
- George, J.; Ishida, H. A Review on the Very High Nanofiller-Content Nanocomposites: Their Preparation Methods and Properties with High Aspect Ratio Fillers. Prog. Polym. Sci. 2018, 86, 1–39.
- Corni, I.; Harvey, T.J.; Wharton, J.A.; Stokes, K.R.; Walsh, F.C.; Wood, R.J.K. A Review of Experimental Techniques to Produce a Nacre-like Structure. Bioinspir. Biomim. 2012, 7, 031001.
- Podsiadlo, P.; Kaushik, A.K.; Arruda, E.M.; Waas, A.M.; Shim, B.S.; Xu, J.; Nandivada, H.; Pumplin, B.G.; Lahann, J.; Ramamoorthy, A.; et al. Ultrastrong and Stiff Layered Polymer Nanocomposites. Science 2007, 318, 80–83.
- Zhu, J.; Zhang, H.; Kotov, N.A. Thermodynamic and Structural Insights into Nanocomposites Engineering by Comparing Two Materials Assembly Techniques for Graphene. ACS Nano 2013, 7, 4818–4829.
- Liu, L.; Gao, Y.; Liu, Q.; Kuang, J.; Zhou, D.; Ju, S.; Han, B.; Zhang, Z. High Mechanical Performance of Layered Graphene Oxide/Poly(Vinyl Alcohol) Nanocomposite Films. Small 2013, 9, 2466–2472.
- Compton, O.C.; Cranford, S.W.; Putz, K.W.; An, Z.; Brinson, L.C.; Buehler, M.J.; Nguyen, S.T. Tuning the Mechanical Properties of Graphene Oxide Paper and Its Associated Polymer Nanocomposites by Controlling Cooperative Intersheet Hydrogen Bonding. ACS Nano 2012, 6, 2008–2019.
- Tian, Y.; Cao, Y.; Wang, Y.; Yang, W.; Feng, J. Realizing Ultrahigh Modulus and High Strength of Macroscopic Graphene Oxide Papers Through Crosslinking of Mussel-Inspired Polymers. Adv. Mater. 2013, 25, 2980–2983.
- Patro, T.U.; Wagner, H.D. Influence of Graphene Oxide Incorporation and Chemical Cross-Linking on Structure and Mechanical Properties of Layer-by-Layer Assembled Poly (Vinyl Alcohol)-Laponite Free-Standing Films. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 2377–2387.
- Wan, S.; Peng, J.; Li, Y.; Hu, H.; Jiang, L.; Cheng, Q. Use of Synergistic Interactions to Fabricate Strong, Tough, and Conductive Arti Fi Cial Nacre Based on Graphene Oxide and Chitosan. ACS Nano 2015, 9, 9830–9836.
- Wu, Y.; Cao, R.; Ji, L.; Huang, W.; Yang, X.; Tu, Y. Synergistic Toughening of Bioinspired Artificial Nacre by Polystyrene Grafted Graphene Oxide. RSC Adv. 2015, 5, 28085–28091.
- Wang, Y.; Li, T.; Ma, P.; Zhang, S.; Zhang, H.; Du, M.; Xie, Y.; Chen, M.; Dong, W.; Ming, W. Artificial Nacre from Supramolecular Assembly of Graphene Oxide. ACS Nano 2018, 12, 6228–6235.
- Cheng, Q.; Wu, M.; Li, M.; Jiang, L.; Tang, Z. Ultratough Artificial Nacre Based on Conjugated Cross-Linked Graphene Oxide. Angew. Chem. Int. Ed. 2013, 52, 3750–3755.
- Li, Y.; Xue, Z.; Luan, Y.; Wang, L.; Zhao, D.; Xu, F.; Xiao, Y.; Guo, Z.; Wang, Z. Improved Mechanical Performance of Graphene Oxide Based Arti Fi Cial Nacre Composites by Regulating the Micro-Laminated Structure and Interface Bonding. Compos. Sci. Technol. 2019, 179, 63–68.
- Wan, S.; Li, Y.; Peng, J.; Hu, H.; Cheng, Q.; Jiang, L. Synergistic Toughening of Graphene Oxide-Molybdenum Disulfide-Thermoplastic Polyurethane Ternary Artificial Nacre. ACS Nano 2015, 9, 708–714.
- Park, S.; Dikin, D.A.; Nguyen, S.T.; Ruoff, R.S. Graphene Oxide Sheets Chemically Cross-Linked by Polyallylamine. J. Phys. Chem. C 2009, 113, 15801–15804.
- Putz, B.K.W.; Compton, O.C.; Palmeri, M.J.; Nguyen, S.T.; Brinson, L.C. High-Nanofiller-Content Graphene Oxide–Polymer Nanocomposites via Vacuum-Assisted Self-Assembly. Adv. Funct. Mater. 2010, 20, 3322–3329.
- Li, Y.; Yu, T.; Yang, T.; Zheng, L.; Liao, K. Bio-Inspired Nacre-like Composite Films Based on Graphene with Superior Mechanical, Electrical, and Biocompatible Properties. Adv. Mater. 2012, 24, 3426–3431.
- Wang, M.; Wang, Q.; Liang, L.; Ding, H.; Liang, X.; Sun, G. High-Content Graphene-Reinforced Polymer with Bioinspired Multilayer Structure. J. Mater. Sci. 2020, 55, 16836–16845.
- Wan, S.; Xu, F.; Jiang, L.; Cheng, Q. Superior Fatigue Resistant Bioinspired Graphene-Based Nanocomposite via Synergistic Interfacial Interactions. Adv. Funct. Mater. 2017, 27, 1703459.
- Gong, S.; Zhang, Q.; Wang, R.; Jiang, L.; Cheng, Q. Synergistically Toughening Nacre-like Graphene Nanocomposites via Gel-Film Transformation. J. Mater. Chem. A 2017, 5, 16386–16392.
- Yang, W.; Zhao, Z.; Wu, K.; Huang, R.; Liu, T.; Jiang, H.; Chen, F.; Fu, Q. Ultrathin Flexible Reduced Graphene Oxide / Cellulose Nanofiber Composite Films with Strongly Anisotropic Thermal Conductivity and Efficient. J. Mater. Chem. C 2017, 5, 3748–3756.
- Hu, K.; Tolentino, L.S.; Kulkarni, D.D.; Ye, C.; Kumar, S.; Tsukruk, V. V Written-in Conductive Patterns on Robust Graphene Oxide Biopaper by Electrochemical Microstamping. Angew. Chem. Int. Ed. 2013, 52, 13784–13788.
- Ni, H.; Xu, F.; Tomsia, A.P.; Saiz, E.; Jiang, L.; Cheng, Q. Robust Bioinspired Graphene Film via π−π Cross-Linking. ACS Appl. Mater. Interfaces 2017, 9, 29.
- Zhang, M.; Huang, L.; Chen, J.; Li, C.; Shi, G. Ultratough, Ultrastrong, and Highly Conductive Graphene Films with Arbitrary Sizes. Adv. Mater. 2014, 26, 7588–7592.
- Cao, J.; Chen, C.; Chen, K.; Lu, Q.; Wang, Q.; Zhou, P.; Liu, D.; Song, L.; Niu, Z.; Chen, J. High-Strength Graphene Composite Films by Molecular Level Couplings for Flexible Supercapacitors with High Volumetric Capacitance. J. Mater. Chem. A 2017, 5, 15008–15016.
- Wan, S.; Hu, H.; Peng, J.; Li, Y.; Fan, Y.; Jiang, L.; Cheng, Q. Nacre-Inspired Integrated Strong and Tough Reduced Graphene Oxide–Poly(Acrylic Acid) Nanocomposites. Nanoscale 2016, 8, 5649–5656.
- Zhao, N.; Yang, M.; Zhao, Q.; Gao, W.; Xie, T.; Bai, H. Superstretchable Nacre-Mimetic Graphene/Poly(Vinyl Alcohol) Composite Film Based on Interfacial Architectural Engineering. ACS Nano 2017, 11, 4777–4784.
- Wang, Y.; Yuan, H.; Ma, P.; Bai, H.; Chen, M.; Dong, W.; Xie, Y.; Deshmukh, Y.S. Superior Performance of Artificial Nacre Based on Graphene Oxide Nanosheets. ACS Appl. Mater. Interfaces 2017, 9, 4215–4222.
- Tang, Z.; Kotov, N.A.; Magonov, S.; Ozturk, B. Nanostructured Artificial Nacre. Nat. Mater. 2003, 2, 413–418.
- Das, P.; Malho, J.M.; Rahimi, K.; Schacher, F.H.; Wang, B.; Demco, D.E.; Walther, A. Nacre-Mimetics with Synthetic Nanoclays up to Ultrahigh Aspect Ratios. Nat. Commun. 2015, 6, 5967.
- Liu, A.; Walther, A.; Ikkala, O.; Belova, L.; Berglund, L.A. Clay Nanopaper with Tough Cellulose Nanofiber Matrix for Fire Retardancy and Gas Barrier Functions. Biomacromolecules 2011, 12, 633–641.
- Walther, A.; Bjurhager, I.; Malho, J.M.; Pere, J.; Ruokolainen, J.; Berglund, L.A.; Ikkala, O. Large-Area, Lightweight and Thick Biomimetic Composites with Superior Material Properties via Fast, Economic, and Green Pathways. Nano Lett. 2010, 10, 2742–2748.
- Wang, J.; Cheng, Q.; Lin, L.; Chen, L.; Jiang, L. Understanding the Relationship of Performance with Nanofiller Content in the Biomimetic Layered Nanocomposites. Nanoscale 2013, 5, 6356–6362.
- Yao, H.B.; Tan, Z.H.; Fang, H.Y.; Yu, S.H. Artificial Nacre-like Bionanocomposite Films from the Self-Assembly of Chitosan-Montmorillonite Hybrid Building Blocks. Angew. Chem. Int. Ed. 2010, 49, 10127–10131.
- Debelak, B.; Lafdi, K. Use of Exfoliated Graphite Filler to Enhance Polymer Physical Properties. Carbon N. Y. 2007, 45, 1727–1734.
- Li, X.; Manasrah, A.; Al-ostaz, A.; Alkhateb, H.; Lincoln, D.; Rushing, G.; Cheng, A.H. Preparation and Characterization of High Content Graphene Nanoplatelet-Polyetherimide Paper. J. Nanosci. Nanoeng. 2015, 1, 252–258.
- Putz, K.W.; Compton, O.C.; Segar, C.; An, Z.; Nguyen, S.T.; Brinson, L.C. Evolution of Order during Vacuum-Assisted Self-Assembly of Graphene Oxide Paper and Associated Polymer Nanocomposites. ACS Nano 2011, 5, 6601–6609.
- Pan, H.; Zhu, S.; Mao, L. Graphene Nanoarchitectonics: Approaching the Excellent Properties of Graphene from Microscale to Macroscale. J. Inorg. Organomet. Polym. Mater. 2015, 25, 179–188.
- An, Z.; Compton, O.C.; Putz, K.W.; Brinson, L.C.; Nguyen, S.T. Bio-Inspired Borate Cross-Linking in Ultra-Stiff Graphene Oxide Thin Films. Adv. Mater. 2011, 23, 3842–3846.
- Park, S.; Lee, K.S.; Bozoklu, G.; Cai, W.; Nguyen, S.B.T.; Ruoff, R.S. Graphene Oxide Papers Modified by Divalent Ions—Enhancing Mechanical Properties via Chemical Cross-Linking. ACS Nano 2008, 2, 572–578.
- Gao, Y.; Liu, L.Q.; Zu, S.Z.; Peng, K.; Zhou, D.; Han, B.H.; Zhang, Z. The Effect of Interlayer Adhesion on the Mechanical Behaviors of Macroscopic Graphene Oxide Papers. ACS Nano 2011, 5, 2134–2141.
- Krishnamoorthy, K.; Veerapandian, M.; Yun, K.; Kim, S.-J. The Chemical and Structural Analysis of Graphene Oxide with Different Degrees of Oxidation. Carbon N. Y. 2013, 53, 38–49.
- Wagner, H.D.; Vaia, R.A. Nanocomposites: Issues at the Interface. Mater. Today 2004, 7, 38–42.
- Galiotis, C.; Young, R.J.; Batchelder, D.N. A Resonance Raman Spectroscopic Study of the Strength of the Bonding between an Epoxy Resin and a Polydiacetylene Fibre. J. Mater. Sci. Lett. 1983, 2, 263–266.
- Melanitis, N.; Galiotis, C. Interfacial Micromechanics in Model Composites Using Laser Raman Spectroscopy. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1993, 440, 379–398.
- Mohiuddin, T.M.G.; Lombardo, A.; Nair, R.R.; Bonetti, A.; Savini, G.; Jalil, R.; Bonini, N.; Basko, D.M.; Galiotis, C.; Marzari, N. Uniaxial Strain in Graphene by Raman Spectroscopy: G Peak Splitting, Grüneisen Parameters, and Sample Orientation. Phys. Rev. B 2009, 79, 205433.
- Bretzlaff, R.S.; Wool, R.P. Frequency Shifting and Asymmetry in Infrared Bands of Stressed Polymers. Macromolecules 1983, 16, 1907–1917.
- Gouadec, G.; Colomban, P. Raman Spectroscopy of Nanomaterials: How Spectra Relate to Disorder, Particle Size and Mechanical Properties. Prog. Cryst. Growth Charact. Mater. 2007, 53, 1–56.
- Tashiro, K.; Gang, W.; Kobayashi, M. Quasiharmonic Treatment of Infrared and Raman Vibrational Frequency Shifts Induced by Tensile Deformation of Polymer Chains. J. Polym. Sci. Part B Polym. Phys. 1990, 28, 2527–2553.
- Begley, M.R.; Philips, N.R.; Compton, B.G.; Wilbrink, D.V.; Ritchie, R.O.; Utz, M. Micromechanical Models to Guide the Development of Synthetic “brick and Mortar” Composites. J. Mech. Phys. Solids 2012, 60, 1545–1560.
- Cox, H.L. The Elasticity and Strength of Paper and Other Fibrous Materials. Br. J. Appl. Phys. 1952, 3, 72–79.
- Kotha, S.P.; Kotha, S.; Guzelsu, N. A Shear-Lag Model to Account for Interaction Effects between Inclusions in Composites Reinforced with Rectangular Platelets. Compos. Sci. Technol. 2000, 60, 2147–2158.
- Pimenta, S.; Robinson, P. An Analytical Shear-Lag Model for Composites with “brick-and-Mortar” Architecture Considering Non-Linear Matrix Response and Failure. Compos. Sci. Technol. 2014, 104, 111–124.
- Wei, X.; Naraghi, M.; Espinosa, H.D. Optimal Length Scales Emerging from Shear Load Transfer in Natural Materials: Application to Carbon-Based Nanocomposite Design. ACS Nano 2012, 6, 2333–2344.
- Barthelat, F. Designing Nacre-like Materials for Simultaneous Stiffness, Strength and Toughness: Optimum Materials, Composition, Microstructure and Size. J. Mech. Phys. Solids 2014, 73, 22–37.
- Abid, N.; Mirkhalaf, M.; Barthelat, F. Discrete-Element Modeling of Nacre-like Materials: Effects of Random Microstructures on Strain Localization and Mechanical Performance. J. Mech. Phys. Solids 2018, 112, 385–402.
- Barthelat, F.; Dastjerdi, A.K.; Rabiei, R. An Improved Failure Criterion for Biological and Engineered Staggered Composites. J. R. Soc. Interface 2013, 10, 20120849.
