1. History

Main page: Chemistry:Discovery of graphene

A lump of graphite, a graphene transistor, and a tape dispenser. Donated to the Nobel Museum in Stockholm by Andre Geim and Konstantin Novoselov in 2010.

Structure of graphite and its intercalation compounds

In 1859, Benjamin Brodie noted the highly lamellar structure of thermally reduced graphite oxide.^[21][22] In 1916, Peter Debye and Paul Scherrer determined the structure of graphite by powder X-ray diffraction.^[23][24][25] The structure was studied in more detail by V. Kohlschütter and P. Haenni in 1918, who also described the properties of graphite oxide paper.^[26] Its structure was determined from single-crystal diffraction in 1924.^[27][28]

The theory of graphene was first explored by P. R. Wallace in 1947 as a starting point for understanding the electronic properties of 3D graphite. The emergent massless Dirac equation was first pointed out in 1984 separately by Gordon Walter Semenoff,^[29] and by David P. DiVincenzo and Eugene J. Mele.^[30] Semenoff emphasized the occurrence in a magnetic field of an electronic Landau level precisely at the Dirac point. This level is responsible for the anomalous integer quantum Hall effect.^[31][32][33]

Observations of thin graphite layers and related structures

Transmission electron microscopy (TEM) images of thin graphite samples consisting of a few graphene layers were published by G. Ruess and F. Vogt in 1948.^[34] Eventually, single layers were also observed directly.^[35] Single layers of graphite were also observed by transmission electron microscopy within bulk materials, in particular inside soot obtained by chemical exfoliation.^[6]

In 1961–1962, Hanns-Peter Boehm published a study of extremely thin flakes of graphite, and coined the term "graphene" for the hypothetical single-layer structure.^[36] This paper reports graphitic flakes that give an additional contrast equivalent of down to ~0.4 nm or 3 atomic layers of amorphous carbon. This was the best possible resolution for 1960 TEMs. However, neither then nor today is it possible to argue how many layers were in those flakes. Now we know that the TEM contrast of graphene most strongly depends on focusing conditions.^[35] For example, it is impossible to distinguish between suspended monolayer and multilayer graphene by their TEM contrasts, and the only known way is to analyze the relative intensities of various diffraction spots. The first reliable TEM observations of monolayers are probably given in refs. 24 and 26 of Geim and Novoselov's 2007 review.^[2]

Starting in the 1970s, C. Oshima and others described single layers of carbon atoms that were grown epitaxially on top of other materials.^[37][38] This "epitaxial graphene" consists of a single-atom-thick hexagonal lattice of sp²-bonded carbon atoms, as in free-standing graphene. However, there is significant charge transfer between the two materials, and, in some cases, hybridization between the d-orbitals of the substrate atoms and π orbitals of graphene; which significantly alter the electronic structure compared to that of free-standing graphene.

The term "graphene" was used again in 1987 to describe single sheets of graphite as a constituent of graphite intercalation compounds,^[39] which can be seen as crystalline salts of the intercalant and graphene. It was also used in the descriptions of carbon nanotubes by R. Saito and Mildred and Gene Dresselhaus in 1992,^[40] and of polycyclic aromatic hydrocarbons in 2000 by S. Wang and others.^[41]

Efforts to make thin films of graphite by mechanical exfoliation started in 1990.^[42] Initial attempts employed exfoliation techniques similar to the drawing method. Multilayer samples down to 10 nm in thickness were obtained.^[2]

In 2002, Robert B. Rutherford and Richard L. Dudman filed for a patent in the US on a method to produce graphene by repeatedly peeling off layers from a graphite flake adhered to a substrate, achieving a graphite thickness of 0.00001 inches (2.5×10⁻⁷ metres). The key to success was high-throughput visual recognition of graphene on a properly chosen substrate, which provides a small but noticeable optical contrast.^[43]

Another U.S. patent was filed in the same year by Bor Z. Jang and Wen C. Huang for a method to produce graphene based on exfoliation followed by attrition.^[44]

In 2014, inventor Larry Fullerton patents a process for producing single layer graphene sheets.^[45]

Full isolation and characterization

Andre Geim and Konstantin Novoselov at the Nobel Laureate press conference, Royal Swedish Academy of Sciences, 2010.

Graphene was properly isolated and characterized in 2004 by Andre Geim and Konstantin Novoselov at the University of Manchester.^[13][14] They pulled graphene layers from graphite with a common adhesive tape in a process called either micromechanical cleavage or the Scotch tape technique.^[46] The graphene flakes were then transferred onto thin silicon dioxide (silica) layer on a silicon plate ("wafer"). The silica electrically isolated the graphene and weakly interacted with it, providing nearly charge-neutral graphene layers. The silicon beneath the SiO₂ could be used as a "back gate" electrode to vary the charge density in the graphene over a wide range.

This work resulted in the two winning the Nobel Prize in Physics in 2010 "for groundbreaking experiments regarding the two-dimensional material graphene."^[47][48][46] Their publication, and the surprisingly easy preparation method that they described, sparked a "graphene gold rush". Research expanded and split off into many different subfields, exploring different exceptional properties of the material—quantum mechanical, electrical, chemical, mechanical, optical, magnetic, etc.

Exploring commercial applications

Since the early 2000s, a number of companies and research laboratories have been working to develop commercial applications of graphene. In 2014 a National Graphene Institute was established with that purpose at the University of Manchester, with a 60 million GBP initial funding.^[49] In North East England two commercial manufacturers, Applied Graphene Materials^[50] and Thomas Swan Limited^[51][52] have begun manufacturing. Cambridge Nanosystems^[53] is a large-scale graphene powder production facility in East Anglia.

2. Structure

Bonding

Carbon orbitals 2s, 2p_x, 2p_y form the hybrid orbital sp² with three major lobes at 120°. The remaining orbital, p_z, is sticking out of the graphene's plane.

Sigma and pi bonds in graphene. Sigma bonds result from an overlap of sp² hybrid orbitals, whereas pi bonds emerge from tunneling between the protruding pz orbitals.

Three of the four outer-shell electrons of each atom in a graphene sheet occupy three sp² hybrid orbitals – a combination of orbitals s, p_x and p_y — that are shared with the three nearest atoms, forming σ-bonds. The length of these bonds is about 0.142 nanometers.^[54][55]

The remaining outer-shell electron occupies a p_z orbital that is oriented perpendicularly to the plane. These orbitals hybridize together to form two half-filled bands of free-moving electrons, π and π∗, which are responsible for most of graphene's notable electronic properties.^[54] Recent quantitative estimates of aromatic stabilization and limiting size derived from the enthalpies of hydrogenation (ΔH_hydro) agree well with the literature reports.^[56]

Graphene sheets stack to form graphite with an interplanar spacing of 0.335 nm (3.35 Å).

Graphene sheets in solid form usually show evidence in diffraction for graphite's (002) layering. This is true of some single-walled nanostructures.^[57] However, unlayered graphene with only (hk0) rings has been found in the core of presolar graphite onions.^[58] TEM studies show faceting at defects in flat graphene sheets^[59] and suggest a role for two-dimensional crystallization from a melt.

Geometry

Scanning probe microscopy image of graphene

The hexagonal lattice structure of isolated, single-layer graphene can be directly seen with transmission electron microscopy (TEM) of sheets of graphene suspended between bars of a metallic grid^[35] Some of these images showed a "rippling" of the flat sheet, with amplitude of about one nanometer. These ripples may be intrinsic to the material as a result of the instability of two-dimensional crystals,^[2][60][61] or may originate from the ubiquitous dirt seen in all TEM images of graphene. Photoresist residue, which must be removed to obtain atomic-resolution images, may be the "adsorbates" observed in TEM images, and may explain the observed rippling.

The hexagonal structure is also seen in scanning tunneling microscope (STM) images of graphene supported on silicon dioxide substrates^[62] The rippling seen in these images is caused by conformation of graphene to the subtrate's lattice, and is not intrinsic.^[62]

Stability

Ab initio calculations show that a graphene sheet is thermodynamically unstable if its size is less than about 20 nm and becomes the most stable fullerene (as within graphite) only for molecules larger than 24,000 atoms.^[63]

3. Properties

Electronic

Main page: Physics:Electronic properties of graphene

Electronic band structure of graphene. Valence and conduction bands meet at the six vertices of the hexagonal Brillouin zone and form linearly dispersing Dirac cones.

Graphene is a zero-gap semiconductor, because its conduction and valence bands meet at the Dirac points. The Dirac points are six locations in momentum space, on the edge of the Brillouin zone, divided into two non-equivalent sets of three points. The two sets are labeled K and K'. The sets give graphene a valley degeneracy of gv = 2. By contrast, for traditional semiconductors the primary point of interest is generally Γ, where momentum is zero.^[54] Four electronic properties separate it from other condensed matter systems.

However, if the in-plane direction is no longer infinite, but confined, its electronic structure would change. They are referred to as graphene nanoribbons. If it is "zig-zag", the bandgap would still be zero. If it is "armchair", the bandgap would be non-zero.

Graphene's hexagonal lattice can be regarded as two interleaving triangular lattices. This perspective was successfully used to calculate the band structure for a single graphite layer using a tight-binding approximation.^[54]

Electronic spectrum

Electrons propagating through graphene's honeycomb lattice effectively lose their mass, producing quasi-particles that are described by a 2D analogue of the Dirac equation rather than the Schrödinger equation for spin-1/2 particles.^[64][65]

Dispersion relation

File:Graphene and Dirac Cones.ogv

The cleavage technique led directly to the first observation of the anomalous quantum Hall effect in graphene in 2005, by Geim's group and by Philip Kim and Yuanbo Zhang. This effect provided direct evidence of graphene's theoretically predicted Berry's phase of massless Dirac fermions and the first proof of the Dirac fermion nature of electrons.^[31][33] These effects had been observed in bulk graphite by Yakov Kopelevich, Igor A. Luk'yanchuk, and others, in 2003–2004.^[66][67]

When the atoms are placed onto the graphene hexagonal lattice, the overlap between the p_z(π) orbitals and the s or the p_x and p_y orbitals is zero by symmetry. The p_z electrons forming the π bands in graphene can therefore be treated independently. Within this π-band approximation, using a conventional tight-binding model, the dispersion relation (restricted to first-nearest-neighbor interactions only) that produces energy of the electrons with wave vector k is^[29][68]

[math]\displaystyle{ E(k_x,k_y)=\pm\,\gamma_0\sqrt{1+4\cos^2{\tfrac{1}{2}ak_x}+4\cos{\tfrac{1}{2}ak_x} \cdot \cos{\tfrac{\sqrt{3}}{2}ak_y}} }[/math]

with the nearest-neighbor (π orbitals) hopping energy γ₀ ≈ 2.8 eV and the lattice constant a ≈ 2.46 Å. The conduction and valence bands, respectively, correspond to the different signs. With one p_z electron per atom in this model the valence band is fully occupied, while the conduction band is vacant. The two bands touch at the zone corners (the K point in the Brillouin zone), where there is a zero density of states but no band gap. The graphene sheet thus displays a semimetallic (or zero-gap semiconductor) character, although the same cannot be said of a graphene sheet rolled into a carbon nanotube, due to its curvature. Two of the six Dirac points are independent, while the rest are equivalent by symmetry. In the vicinity of the K-points the energy depends linearly on the wave vector, similar to a relativistic particle.^[29][69] Since an elementary cell of the lattice has a basis of two atoms, the wave function has an effective 2-spinor structure.

As a consequence, at low energies, even neglecting the true spin, the electrons can be described by an equation that is formally equivalent to the massless Dirac equation. Hence, the electrons and holes are called Dirac fermions.^[29] This pseudo-relativistic description is restricted to the chiral limit, i.e., to vanishing rest mass M₀, which leads to interesting additional features:^[29][70]

[math]\displaystyle{ v_F\, \vec \sigma \cdot \nabla \psi(\mathbf{r})\,=\,E\psi(\mathbf{r}). }[/math]

Here v_F ~ 10⁶ m/s (.003 c) is the Fermi velocity in graphene, which replaces the velocity of light in the Dirac theory; [math]\displaystyle{ \vec{\sigma} }[/math] is the vector of the Pauli matrices, [math]\displaystyle{ \psi(\mathbf{r}) }[/math] is the two-component wave function of the electrons, and E is their energy.^[64]

The equation describing the electrons' linear dispersion relation is

[math]\displaystyle{ E(q)=\hbar v_F q }[/math]

where the wavevector q is measured from the Brillouin zone vertex K, [math]\displaystyle{ q=\left|\mathbf{k}-\mathrm{K}\right| }[/math], and the zero of energy is set to coincide with the Dirac point. The equation uses a pseudospin matrix formula that describes two sublattices of the honeycomb lattice.^[69]

Single-atom wave propagation

Electron waves in graphene propagate within a single-atom layer, making them sensitive to the proximity of other materials such as high-κ dielectrics, superconductors and ferromagnetics.

Ambipolar electron and hole transport

When the gate voltage in a field effect graphene device is changed from positive to negative, conduction switches from electrons to holes. The charge carrier concentration is proportional to the applied voltage. Graphene is neutral at zero gate voltage and resistivity is at its maximum because of the dearth of charge carriers. The rapid fall of resistivity when carriers are injected shows their high mobility, here of the order of 5000 cm²/Vs. n-Si/SiO₂ substrate, T=1K.^[2]

Graphene displays remarkable electron mobility at room temperature, with reported values in excess of 15000 cm²⋅V⁻¹⋅s⁻¹.^[2] Hole and electron mobilities are nearly the same.^[65] The mobility is independent of temperature between 10 K and 100 K,^[31][71][72] and shows little change even at room temperature (300 K),^[2] which implies that the dominant scattering mechanism is defect scattering. Scattering by graphene's acoustic phonons intrinsically limits room temperature mobility in freestanding graphene to 200000 cm²⋅V⁻¹⋅s⁻¹ at a carrier density of 10¹² cm⁻².^[72][73]

The corresponding resistivity of graphene sheets would be 10⁻⁶ Ω⋅cm. This is less than the resistivity of silver, the lowest otherwise known at room temperature.^[74] However, on SiO₂ substrates, scattering of electrons by optical phonons of the substrate is a larger effect than scattering by graphene's own phonons. This limits mobility to 40000 cm²⋅V⁻¹⋅s⁻¹.^[72]

Charge transport has major concerns due to adsorption of contaminants such as water and oxygen molecules. This leads to non-repetitive and large hysteresis I-V characteristics. Researchers must carry out electrical measurements in vacuum. The protection of graphene surface by a coating with materials such as SiN, PMMA, h-BN, etc., have been discussed by researchers. In January 2015, the first stable graphene device operation in air over several weeks was reported, for graphene whose surface was protected by aluminum oxide.^[75][76] In 2015, lithium-coated graphene exhibited superconductivity, a first for graphene.^[77]

Electrical resistance in 40-nanometer-wide nanoribbons of epitaxial graphene changes in discrete steps. The ribbons' conductance exceeds predictions by a factor of 10. The ribbons can act more like optical waveguides or quantum dots, allowing electrons to flow smoothly along the ribbon edges. In copper, resistance increases in proportion to length as electrons encounter impurities.^[78][79]

Transport is dominated by two modes. One is ballistic and temperature-independent, while the other is thermally activated. Ballistic electrons resemble those in cylindrical carbon nanotubes. At room temperature, resistance increases abruptly at a particular length—the ballistic mode at 16 micrometres and the other at 160 nanometres (1% of the former length).^[78]

Graphene electrons can cover micrometer distances without scattering, even at room temperature.^[64]

Despite zero carrier density near the Dirac points, graphene exhibits a minimum conductivity on the order of [math]\displaystyle{ 4e^2/h }[/math]. The origin of this minimum conductivity is still unclear. However, rippling of the graphene sheet or ionized impurities in the SiO₂ substrate may lead to local puddles of carriers that allow conduction.^[65] Several theories suggest that the minimum conductivity should be [math]\displaystyle{ 4e^2/{(\pi}h) }[/math]; however, most measurements are of order [math]\displaystyle{ 4e^2/h }[/math] or greater^[2] and depend on impurity concentration.^[80]

Near zero carrier density graphene exhibits positive photoconductivity and negative photoconductivity at high carrier density. This is governed by the interplay between photoinduced changes of both the Drude weight and the carrier scattering rate.^[81]

Graphene doped with various gaseous species (both acceptors and donors) can be returned to an undoped state by gentle heating in vacuum.^[80][82] Even for dopant concentrations in excess of 10¹² cm⁻² carrier mobility exhibits no observable change.^[82] Graphene doped with potassium in ultra-high vacuum at low temperature can reduce mobility 20-fold.^[80][83] The mobility reduction is reversible on heating the graphene to remove the potassium.

Due to graphene's two dimensions, charge fractionalization (where the apparent charge of individual pseudoparticles in low-dimensional systems is less than a single quantum^[84]) is thought to occur. It may therefore be a suitable material for constructing quantum computers^[85] using anyonic circuits.^[86]

Chiral half-integer quantum Hall effect

Landau levels in graphene appear at energies proportional to √N, in contrast to the standard sequence that goes as N+1/2.^[2]

The quantum Hall effect is a quantum mechanical version of the Hall effect, which is the production of transverse (perpendicular to the main current) conductivity in the presence of a magnetic field. The quantization of the Hall effect [math]\displaystyle{ \sigma_{xy} }[/math] at integer multiples (the "Landau level") of the basic quantity [math]\displaystyle{ e^2/h }[/math] (where e is the elementary electric charge and h is Planck's constant). It can usually be observed only in very clean silicon or gallium arsenide solids at temperatures around 3 K and very high magnetic fields.

Graphene shows the quantum Hall effect with respect to conductivity quantization: the effect is unordinary in that the sequence of steps is shifted by 1/2 with respect to the standard sequence and with an additional factor of 4. Graphene's Hall conductivity is [math]\displaystyle{ \sigma_{xy}=\pm {4\cdot\left(N + 1/2 \right)e^2}/h }[/math], where N is the Landau level and the double valley and double spin degeneracies give the factor of 4.^[2] These anomalies are present not only at extremely low temperatures but also at room temperature, i.e. at roughly 20 °C (293 K).^[31]

This behavior is a direct result of graphene's chiral, massless Dirac electrons.^[2][87] In a magnetic field, their spectrum has a Landau level with energy precisely at the Dirac point. This level is a consequence of the Atiyah–Singer index theorem and is half-filled in neutral graphene,^[29] leading to the "+1/2" in the Hall conductivity.^[32] Bilayer graphene also shows the quantum Hall effect, but with only one of the two anomalies (i.e. [math]\displaystyle{ \sigma_{xy}=\pm {4\cdot N\cdot e^2}/h }[/math]). In the second anomaly, the first plateau at N=0 is absent, indicating that bilayer graphene stays metallic at the neutrality point.^[2]

Chiral half-integer quantum Hall effect in graphene. Plateaux in transverse conductivity appear at half integers of 4e²/h.^[2]

Unlike normal metals, graphene's longitudinal resistance shows maxima rather than minima for integral values of the Landau filling factor in measurements of the Shubnikov–de Haas oscillations, whereby the term integral quantum Hall effect. These oscillations show a phase shift of π, known as Berry's phase.^[31][65] Berry's phase arises due to chirality or dependence (locking) of the pseudospin quantum number on momentum of low-energy electrons near the Dirac points.^[33] The temperature dependence of the oscillations reveals that the carriers have a non-zero cyclotron mass, despite their zero effective mass in the Dirac-fermion formalism.^[31]

Graphene samples prepared on nickel films, and on both the silicon face and carbon face of silicon carbide, show the anomalous effect directly in electrical measurements.^{[88][89][90][91][92][93]} Graphitic layers on the carbon face of silicon carbide show a clear Dirac spectrum in angle-resolved photoemission experiments, and the effect is observed in cyclotron resonance and tunneling experiments.^[94]

Strong magnetic fields

In magnetic fields above 10 tesla or so additional plateaus of the Hall conductivity at σ_xy = νe²/h with ν = 0, ±1, ±4 are observed.^[95] A plateau at ν = 3^[96] and the fractional quantum Hall effect at ν = 1/3 were also reported.^[96][97]

These observations with ν = 0, ±1, ±3, ±4 indicate that the four-fold degeneracy (two valley and two spin degrees of freedom) of the Landau energy levels is partially or completely lifted.

Casimir effect

The Casimir effect is an interaction between disjoint neutral bodies provoked by the fluctuations of the electrodynamical vacuum. Mathematically it can be explained by considering the normal modes of electromagnetic fields, which explicitly depend on the boundary (or matching) conditions on the interacting bodies' surfaces. Since graphene/electromagnetic field interaction is strong for a one-atom-thick material, the Casimir effect is of growing interest.^[98][99]

Van der Waals force

The Van der Waals force (or dispersion force) is also unusual, obeying an inverse cubic, asymptotic power law in contrast to the usual inverse quartic.^[100]

'Massive' electrons

Graphene's unit cell has two identical carbon atoms and two zero-energy states: one in which the electron resides on atom A, the other in which the electron resides on atom B. However, if the two atoms in the unit cell are not identical, the situation changes. Hunt et al. show that placing hexagonal boron nitride (h-BN) in contact with graphene can alter the potential felt at atom A versus atom B enough that the electrons develop a mass and accompanying band gap of about 30 meV [0.03 Electron Volt(eV)].^[101]

The mass can be positive or negative. An arrangement that slightly raises the energy of an electron on atom A relative to atom B gives it a positive mass, while an arrangement that raises the energy of atom B produces a negative electron mass. The two versions behave alike and are indistinguishable via optical spectroscopy. An electron traveling from a positive-mass region to a negative-mass region must cross an intermediate region where its mass once again becomes zero. This region is gapless and therefore metallic. Metallic modes bounding semiconducting regions of opposite-sign mass is a hallmark of a topological phase and display much the same physics as topological insulators.^[101]

If the mass in graphene can be controlled, electrons can be confined to massless regions by surrounding them with massive regions, allowing the patterning of quantum dots, wires, and other mesoscopic structures. It also produces one-dimensional conductors along the boundary. These wires would be protected against backscattering and could carry currents without dissipation.^[101]

Permittivity

Graphene's permittivity varies with frequency. Over a range from microwave to millimeter wave frequencies it is roughly 3.3.^[102] This permittivity, combined with the ability to form both conductors and insulators, means that theoretically, compact capacitors made of graphene could store large amounts of electrical energy.

Optical

Graphene's unique optical properties produce an unexpectedly high opacity for an atomic monolayer in vacuum, absorbing πα ≈ 2.3% of light, from visible to infrared.^[8][9][103] Here, α is the fine-structure constant. This is a consequence of the "unusual low-energy electronic structure of monolayer graphene that features electron and hole conical bands meeting each other at the Dirac point... [which] is qualitatively different from more common quadratic massive bands."^[8] Based on the Slonczewski–Weiss–McClure (SWMcC) band model of graphite, the interatomic distance, hopping value and frequency cancel when optical conductance is calculated using Fresnel equations in the thin-film limit.

Although confirmed experimentally, the measurement is not precise enough to improve on other techniques for determining the fine-structure constant.^[104]

Multi-Parametric Surface Plasmon Resonance was used to characterize both thickness and refractive index of chemical-vapor-deposition (CVD)-grown graphene films. The measured refractive index and extinction coefficient values at 670 nm (6.7×10⁻⁷ m) wavelength are 3.135 and 0.897, respectively. The thickness was determined as 3.7Å from a 0.5mm area, which agrees with 3.35Å reported for layer-to-layer carbon atom distance of graphite crystals.^[105] The method can be further used also for real-time label-free interactions of graphene with organic and inorganic substances. Furthermore, the existence of unidirectional surface plasmons in the nonreciprocal graphene-based gyrotropic interfaces has been demonstrated theoretically. By efficiently controlling the chemical potential of graphene, the unidirectional working frequency can be continuously tunable from THz to near-infrared and even visible.^[106] Particularly, the unidirectional frequency bandwidth can be 1– 2 orders of magnitude larger than that in metal under the same magnetic field, which arises from the superiority of extremely small effective electron mass in graphene.

Graphene's band gap can be tuned from 0 to 0.25 eV (about 5 micrometre wavelength) by applying voltage to a dual-gate bilayer graphene field-effect transistor (FET) at room temperature.^[107] The optical response of graphene nanoribbons is tunable into the terahertz regime by an applied magnetic field.^[108] Graphene/graphene oxide systems exhibit electrochromic behavior, allowing tuning of both linear and ultrafast optical properties.^[109]

A graphene-based Bragg grating (one-dimensional photonic crystal) has been fabricated and demonstrated its capability for excitation of surface electromagnetic waves in the periodic structure by using 633 nm (6.33×10⁻⁷ m) He–Ne laser as the light source.^[110]

Saturable absorption

Such unique absorption could become saturated when the input optical intensity is above a threshold value. This nonlinear optical behavior is termed saturable absorption and the threshold value is called the saturation fluence. Graphene can be saturated readily under strong excitation over the visible to near-infrared region, due to the universal optical absorption and zero band gap. This has relevance for the mode locking of fiber lasers, where fullband mode locking has been achieved by graphene-based saturable absorber. Due to this special property, graphene has wide application in ultrafast photonics. Moreover, the optical response of graphene/graphene oxide layers can be tuned electrically.^{[109][111][112][113][114][115]}

Saturable absorption in graphene could occur at the Microwave and Terahertz band, owing to its wideband optical absorption property. The microwave saturable absorption in graphene demonstrates the possibility of graphene microwave and terahertz photonics devices, such as a microwave saturable absorber, modulator, polarizer, microwave signal processing and broad-band wireless access networks.^[116]

Nonlinear Kerr effect

Under more intensive laser illumination, graphene could also possess a nonlinear phase shift due to the optical nonlinear Kerr effect. Based on a typical open and close aperture z-scan measurement, graphene possesses a giant nonlinear Kerr coefficient of 10⁻⁷ cm²⋅W⁻¹, almost nine orders of magnitude larger than that of bulk dielectrics.^[117] This suggests that graphene may be a powerful nonlinear Kerr medium, with the possibility of observing a variety of nonlinear effects, the most important of which is the soliton.^[118]

Excitonic

First-principle calculations with quasiparticle corrections and many-body effects are performed to study the electronic and optical properties of graphene-based materials. The approach is described as three stages.^[119] With GW calculation, the properties of graphene-based materials are accurately investigated, including bulk graphene,^[120] nanoribbons,^[121] edge and surface functionalized armchair oribbons,^[122] hydrogen saturated armchair ribbons,^[123] Josephson effect in graphene SNS junctions with single localized defect^[124] and armchair ribbon scaling properties.^[125]

Spin transport

Graphene is claimed to be an ideal material for spintronics due to its small spin–orbit interaction and the near absence of nuclear magnetic moments in carbon (as well as a weak hyperfine interaction). Electrical spin current injection and detection has been demonstrated up to room temperature.^{[126][127][128]} Spin coherence length above 1 micrometre at room temperature was observed,^[126] and control of the spin current polarity with an electrical gate was observed at low temperature.^[127]

Magnetic properties

Strong magnetic fields

Graphene's quantum Hall effect in magnetic fields above 10 Teslas or so reveals additional interesting features. Additional plateaus of the Hall conductivity at [math]\displaystyle{ \sigma_{xy}=\nu e^2/h }[/math] with [math]\displaystyle{ \nu=0,\pm {1},\pm {4} }[/math] are observed.^[95] Also, the observation of a plateau at [math]\displaystyle{ \nu=3 }[/math]^[96] and the fractional quantum Hall effect at [math]\displaystyle{ \nu=1/3 }[/math] were reported.^[96][97]

These observations with [math]\displaystyle{ \nu=0,\pm 1,\pm 3, \pm 4 }[/math] indicate that the four-fold degeneracy (two valley and two spin degrees of freedom) of the Landau energy levels is partially or completely lifted. One hypothesis is that the magnetic catalysis of symmetry breaking is responsible for lifting the degeneracy.

Spintronic and magnetic properties can be present in graphene simultaneously.^[129] Low-defect graphene nanomeshes manufactured by using a non-lithographic method exhibit large-amplitude ferromagnetism even at room temperature. Additionally a spin pumping effect is found for fields applied in parallel with the planes of few-layer ferromagnetic nanomeshes, while a magnetoresistance hysteresis loop is observed under perpendicular fields.

Magnetic substrates

In 2014 researchers magnetized graphene by placing it on an atomically smooth layer of magnetic yttrium iron garnet. The graphene's electronic properties were unaffected. Prior approaches involved doping graphene with other substances.^[130] The dopant's presence negatively affected its electronic properties.^[131]

Thermal conductivity

Thermal transport in graphene is an active area of research, which has attracted attention because of the potential for thermal management applications. Following predictions for graphene and related carbon nanotubes,^[132] early measurements of the thermal conductivity of suspended graphene reported an exceptionally large thermal conductivity up to 5300 W⋅m⁻¹⋅K⁻¹,^[133] compared with the thermal conductivity of pyrolytic graphite of approximately 2000 W⋅m⁻¹⋅K⁻¹ at room temperature.^[134] However, later studies primarily on more scalable but more defected graphene derived by Chemical Vapor Deposition have been unable to reproduce such high thermal conductivity measurements, producing a wide range of thermal conductivities between 1500 – 2500 W⋅m⁻¹⋅K⁻¹ for suspended single layer graphene .^{[135][136][137][138]} The large range in the reported thermal conductivity can be caused by large measurement uncertainties as well as variations in the graphene quality and processing conditions. In addition, it is known that when single-layer graphene is supported on an amorphous material, the thermal conductivity is reduced to about 500 – 600 W⋅m⁻¹⋅K⁻¹ at room temperature as a result of scattering of graphene lattice waves by the substrate,^[139][140] and can be even lower for few layer graphene encased in amorphous oxide.^[141] Likewise, polymeric residue can contribute to a similar decrease in the thermal conductivity of suspended graphene to approximately 500 – 600 W⋅m⁻¹⋅K⁻¹ for bilayer graphene.^[142]

It has been suggested that the isotopic composition, the ratio of ¹²C to ¹³C, has a significant impact on the thermal conductivity. For example, isotopically pure ¹²C graphene has higher thermal conductivity than either a 50:50 isotope ratio or the naturally occurring 99:1 ratio.^[143] It can be shown by using the Wiedemann–Franz law, that the thermal conduction is phonon-dominated.^[133] However, for a gated graphene strip, an applied gate bias causing a Fermi energy shift much larger than k_BT can cause the electronic contribution to increase and dominate over the phonon contribution at low temperatures. The ballistic thermal conductance of graphene is isotropic.^[144][145]

Potential for this high conductivity can be seen by considering graphite, a 3D version of graphene that has basal plane thermal conductivity of over a 1000 W⋅m⁻¹⋅K⁻¹ (comparable to diamond). In graphite, the c-axis (out of plane) thermal conductivity is over a factor of ~100 smaller due to the weak binding forces between basal planes as well as the larger lattice spacing.^[146] In addition, the ballistic thermal conductance of graphene is shown to give the lower limit of the ballistic thermal conductances, per unit circumference, length of carbon nanotubes.^[147]

Despite its 2-D nature, graphene has 3 acoustic phonon modes. The two in-plane modes (LA, TA) have a linear dispersion relation, whereas the out of plane mode (ZA) has a quadratic dispersion relation. Due to this, the T² dependent thermal conductivity contribution of the linear modes is dominated at low temperatures by the T^1.5 contribution of the out of plane mode.^[147] Some graphene phonon bands display negative Grüneisen parameters.^[148] At low temperatures (where most optical modes with positive Grüneisen parameters are still not excited) the contribution from the negative Grüneisen parameters will be dominant and thermal expansion coefficient (which is directly proportional to Grüneisen parameters) negative. The lowest negative Grüneisen parameters correspond to the lowest transverse acoustic ZA modes. Phonon frequencies for such modes increase with the in-plane lattice parameter since atoms in the layer upon stretching will be less free to move in the z direction. This is similar to the behavior of a string, which, when it is stretched, will have vibrations of smaller amplitude and higher frequency. This phenomenon, named "membrane effect," was predicted by Lifshitz in 1952.^[149]

Mechanical

The (two-dimensional) density of graphene is 0.763 mg per square meter.

Graphene is the strongest material ever tested,^[10][11] with an intrinsic tensile strength of 130 GPa (19,000,000 psi) (with representative engineering tensile strength ~50-60 GPa for stretching large-area freestanding graphene) and a Young's modulus (stiffness) close to 1 TPa (150,000,000 psi). The Nobel announcement illustrated this by saying that a 1 square meter graphene hammock would support a 4 kg cat but would weigh only as much as one of the cat's whiskers, at 0.77 mg (about 0.001% of the weight of 1 m² of paper).^[150]

Large-angle-bent graphene monolayer has been achieved with negligible strain, showing mechanical robustness of the two-dimensional carbon nanostructure. Even with extreme deformation, excellent carrier mobility in monolayer graphene can be preserved.^[151]

The spring constant of suspended graphene sheets has been measured using an atomic force microscope (AFM). Graphene sheets were suspended over SiO₂ cavities where an AFM tip was used to apply a stress to the sheet to test its mechanical properties. Its spring constant was in the range 1–5 N/m and the stiffness was 0.5 TPa, which differs from that of bulk graphite. These intrinsic properties could lead to applications such as NEMS as pressure sensors and resonators.^[152] Due to its large surface energy and out of plane ductility, flat graphene sheets are unstable with respect to scrolling, i.e. bending into a cylindrical shape, which is its lower-energy state.^[153]

As is true of all materials, regions of graphene are subject to thermal and quantum fluctuations in relative displacement. Although the amplitude of these fluctuations is bounded in 3D structures (even in the limit of infinite size), the Mermin–Wagner theorem shows that the amplitude of long-wavelength fluctuations grows logarithmically with the scale of a 2D structure, and would therefore be unbounded in structures of infinite size. Local deformation and elastic strain are negligibly affected by this long-range divergence in relative displacement. It is believed that a sufficiently large 2D structure, in the absence of applied lateral tension, will bend and crumple to form a fluctuating 3D structure. Researchers have observed ripples in suspended layers of graphene,^[35] and it has been proposed that the ripples are caused by thermal fluctuations in the material. As a consequence of these dynamical deformations, it is debatable whether graphene is truly a 2D structure.^{[2][60][61][154][155]} It has recently been shown that these ripples, if amplified through the introduction of vacancy defects, can impart a negative Poisson's ratio into graphene, resulting in the thinnest auxetic material known so far.^[156]

Graphene nanosheets have been incorporated into a Ni matrix through a plating process to form Ni-graphene composites on a target substrate. The enhancement in mechanical properties of the composites is attributed to the high interaction between Ni and graphene and the prevention of the dislocation sliding in the Ni matrix by the graphene.^[157]

Fracture toughness

In 2014, researchers from Rice University and the Georgia Institute of Technology have indicated that despite its strength, graphene is also relatively brittle, with a fracture toughness of about 4 MPa√m.^[158] This indicates that imperfect graphene is likely to crack in a brittle manner like ceramic materials, as opposed to many metallic materials which tend to have fracture toughnesses in the range of 15–50 MPa√m. Later in 2014, the Rice team announced that graphene showed a greater ability to distribute force from an impact than any known material, ten times that of steel per unit weight.^[159] The force was transmitted at 22.2 kilometres per second (13.8 mi/s).^[160]

Polycrystalline graphene

Various methods – most notably, chemical vapor deposition (CVD), as discussed in the section below - have been developed to produce large-scale graphene needed for device applications. Such methods often synthesize polycrystalline graphene.^[161] The mechanical properties of polycrystalline graphene is affected by the nature of the defects, such as grain-boundaries (GB) and vacancies, present in the system and the average grain-size. How the mechanical properties change with such defects have been investigated by researchers, theoretically and experimentally.^{[162][161][163][164]}

Graphene grain boundaries typically contain heptagon-pentagon pairs. The arrangement of such defects depends on whether the GB is in zig-zag or armchair direction. It further depends on the tilt-angle of the GB.^[165] In 2010, researchers from Brown University computationally predicted that as the tilt-angle increases, the grain boundary strength also increases. They showed that the weakest link in the grain boundary is at the critical bonds of the heptagon rings. As the grain boundary angle increases, the strain in these heptagon rings decreases, causing the grain-boundary to be stronger than lower-angle GBs. They proposed that, in fact, for sufficiently large angle GB, the strength of the GB is similar to pristine graphene.^[166] In 2012, it was further shown that the strength can increase or decrease, depending on the detailed arrangements of the defects.^[167] These predictions have since been supported by experimental evidences. In a 2013 study led by James Hone's group, researchers probed the elastic stiffness and strength of CVD-grown graphene by combining nano-indentation and high-resolution TEM. They found that the elastic stiffness is identical and strength is only slightly lower than those in pristine graphene.^[168] In the same year, researchers from UC Berkeley and UCLA probed bi-crystalline graphene with TEM and AFM. They found that the strength of grain-boundaries indeed tend to increase with the tilt angle.^[169]

While the presence of vacancies is not only prevalent in polycrystalline graphene, vacancies can have significant effects on the strength of graphene. The general consensus is that the strength decreases along with increasing densities of vacancies. In fact, various studies have shown that for graphene with sufficiently low density of vacancies, the strength does not vary significantly from that of pristine graphene. On the other hand, high density of vacancies can severely reduce the strength of graphene.^[163]

Compared to the fairly well-understood nature of the effect that grain boundary and vacancies have on the mechanical properties of graphene, there is no clear consensus on the general effect that the average grain size has on the strength of polycrystalline graphene.^{[162][163][164]} In fact, three notable theoretical/computational studies on this topic have led to three different conclusions.^{[170][171][172]} First, in 2012, Kotakoski and Myer studied the mechanical properties of polycrystalline graphene with "realistic atomistic model", using molecular-dynamics (MD) simulation. To emulate the growth mechanism of CVD, they first randomly selected nucleation sites that are at least 5A (arbitrarily chosen) apart from other sites. Polycrystalline graphene was generated from these nucleation sites and was subsequently annealed at 3000K, then quenched. Based on this model, they found that cracks are initiated at grain-boundary junctions, but the grain size does not significantly affect the strength.^[170] Second, in 2013, Z. Song et al. used MD simulations to study the mechanical properties of polycrystalline graphene with uniform-sized hexagon-shaped grains. The hexagon grains were oriented in various lattice directions and the GBs consisted of only heptagon, pentagon, and hexagonal carbon rings. The motivation behind such model was that similar systems had been experimentally observed in graphene flakes grown on the surface of liquid copper. While they also noted that crack is typically initiated at the triple junctions, they found that as the grain size decreases, the yield strength of graphene increases. Based on this finding, they proposed that polycrystalline follows pseudo Hall-Petch relationship.^[171] Third, in 2013, Z. D. Sha et al. studied the effect of grain size on the properties of polycrystalline graphene, by modelling the grain patches using Voronoi construction. The GBs in this model consisted of heptagon, pentagon, and hexagon, as well as squares, octagons, and vacancies. Through MD simulation, contrary to the fore-mentioned study, they found inverse Hall-Petch relationship, where the strength of graphene increases as the grain size increases.^[172] Experimental observations and other theoretical predictions also gave differing conclusions, similar to the three given above.^[164] Such discrepancies show the complexity of the effects that grain size, arrangements of defects, and the nature of defects have on the mechanical properties of polycrystalline graphene.

Chemical

Graphene has a theoretical specific surface area (SSA) of 2630 m²/g. This is much larger than that reported to date for carbon black (typically smaller than 900 m²/g) or for carbon nanotubes (CNTs), from ≈100 to 1000 m²/g and is similar to activated carbon.^[173] Graphene is the only form of carbon (or solid material) in which every atom is available for chemical reaction from two sides (due to the 2D structure). Atoms at the edges of a graphene sheet have special chemical reactivity. Graphene has the highest ratio of edge atoms of any allotrope. Defects within a sheet increase its chemical reactivity.^[174] The onset temperature of reaction between the basal plane of single-layer graphene and oxygen gas is below 260 °C (530 K).^[175] Graphene burns at very low temperature (e.g., 350 °C (620 K)).^[176] Graphene is commonly modified with oxygen- and nitrogen-containing functional groups and analyzed by infrared spectroscopy and X-ray photoelectron spectroscopy. However, determination of structures of graphene with oxygen-^[177] and nitrogen-^[178] functional groups requires the structures to be well controlled.

In 2013, Stanford University physicists reported that single-layer graphene is a hundred times more chemically reactive than thicker multilayer sheets.^[179]

Graphene can self-repair holes in its sheets, when exposed to molecules containing carbon, such as hydrocarbons. Bombarded with pure carbon atoms, the atoms perfectly align into hexagons, completely filling the holes.^[180][181]

Biological

Despite the promising results in different cell studies and proof of concept studies, there is still incomplete understanding of the full biocompatibility of graphene based materials.^[182] Different cell lines react differently when exposed to graphene, and it has been shown that the lateral size of the graphene flakes, the form and surface chemistry can elicit different biological responses on the same cell line.^[183]

There are indications that graphene has promise as a useful material for interacting with neural cells; studies on cultured neural cells show limited success.^[184][185]

Graphene also has some utility in osteogenics. Researchers at the Graphene Research Centre at the National University of Singapore (NUS) discovered in 2011 the ability of graphene to accelerate the osteogenic differentiation of human Mesenchymal Stem Cells without the use of biochemical inducers.^[186]

Graphene can be used in biosensors; in 2015, researchers demonstrated that a graphene-based sensor be can used to detect a cancer risk biomarker. In particular, by using epitaxial graphene on silicon carbide, they were repeatably able to detect 8-hydroxydeoxyguanosine (8-OHdG), a DNA damage biomarker.^[187]

Support substrate

The electronics property of graphene can be significantly influenced by the supporting substrate. Studies of graphene monolayers on clean and hydrogen(H)-passivated silicon (100) (Si(100)/H) surfaces have been performed.^[188] The Si(100)/H surface does not perturb the electronic properties of graphene, whereas the interaction between the clean Si(100) surface and graphene changes the electronic states of graphene significantly. This effect results from the covalent bonding between C and surface Si atoms, modifying the π-orbital network of the graphene layer. The local density of states shows that the bonded C and Si surface states are highly disturbed near the Fermi energy.

4. Forms

Monolayer sheets

In 2013 a group of Polish scientists presented a production unit that allows the manufacture of continuous monolayer sheets.^[189] The process is based on graphene growth on a liquid metal matrix.^[190] The product of this process was called High Strength Metallurgical Graphene. In a new study published in Nature, the researchers have used a single layer graphene electrode and a novel surface sensitive non-linear spectroscopy technique to investigate the top-most water layer at the electrochemically charged surface. They found that the interfacial water response to applied electric field is asymmetric with respect to the nature of the applied field.^[191]

Bilayer graphene

Main page: Physics:Bilayer graphene

Bilayer graphene displays the anomalous quantum Hall effect, a tunable band gap^[192] and potential for excitonic condensation^[193] –making it a promising candidate for optoelectronic and nanoelectronic applications. Bilayer graphene typically can be found either in twisted configurations where the two layers are rotated relative to each other or graphitic Bernal stacked configurations where half the atoms in one layer lie atop half the atoms in the other.^[194] Stacking order and orientation govern the optical and electronic properties of bilayer graphene.

One way to synthesize bilayer graphene is via chemical vapor deposition, which can produce large bilayer regions that almost exclusively conform to a Bernal stack geometry.^[194]

It has been shown that the two graphene layers can withstand important strain or doping mismatch^[195] which ultimately should lead to their exfoliation.

Turbostratic graphene

Turbostratic graphene exhibits weak interlayer coupling, and the spacing is increased with respect to Bernal-stacked multilayer graphene. Rotational misalignment preserves the 2D electronic structure, as confirmed by Raman spectroscopy. The D peak is very weak, whereas the 2D and G peaks remain prominent. A rather peculiar feature is that the I_2D/I_G ratio can exceed 10. However, most importantly, the M peak, which originates from AB stacking, is absent, whereas the TS₁ and TS₂ modes are visible in the Raman spectrum.^[196][197] The material is formed through conversion of non-graphenic carbon into graphenic carbon without providing sufficient energy to allow for the reorganization through annealing of adjacent graphene layers into crystalline graphitic structures.

Graphene superlattices

Periodically stacked graphene and its insulating isomorph provide a fascinating structural element in implementing highly functional superlattices at the atomic scale, which offers possibilities in designing nanoelectronic and photonic devices. Various types of superlattices can be obtained by stacking graphene and its related forms.^[198] The energy band in layer-stacked superlattices is found to be more sensitive to the barrier width than that in conventional III–V semiconductor superlattices. When adding more than one atomic layer to the barrier in each period, the coupling of electronic wavefunctions in neighboring potential wells can be significantly reduced, which leads to the degeneration of continuous subbands into quantized energy levels. When varying the well width, the energy levels in the potential wells along the L-M direction behave distinctly from those along the K-H direction.

A superlattice corresponds to a periodic or quasi-periodic arrangement of different materials, and can be described by a superlattice period which confers a new translational symmetry to the system, impacting their phonon dispersions and subsequently their thermal transport properties. Recently, uniform monolayer graphene-hBN structures have been successfully synthesized via lithography patterning coupled with chemical vapor deposition (CVD).^[199] Furthermore, superlattices of graphene-hBN are ideal model systems for the realization and understanding of coherent (wave-like) and incoherent (particle-like) phonon thermal transport.^{[200][201][202][203][204]}

Graphene nanoribbons

Names for graphene edge topologies

GNR Electronic band structure of graphene strips of varying widths in zig-zag orientation. Tight-binding calculations show that they are all metallic.

GNR Electronic band structure of graphene strips of various widths in the armchair orientation. Tight-binding calculations show that they are semiconducting or metallic depending on width (chirality).

Graphene nanoribbons ("nanostripes" in the "zig-zag"/"zigzag" orientation), at low temperatures, show spin-polarized metallic edge currents, which also suggests applications in the new field of spintronics. (In the "armchair" orientation, the edges behave like semiconductors.^[64])

Graphene quantum dots

A graphene quantum dot (GQD) is a graphene fragment with size less than 100 nm. The properties of GQDs are different from 'bulk' graphene due to the quantum confinement effects which only becomes apparent when size is smaller than 100 nm.^{[205][206][207]}

Graphene oxide

Graphene oxide is usually produced through chemical exfoliation of graphite. A particularly popular technique is the improved Hummer's method.^[208] Using paper-making techniques on dispersed, oxidized and chemically processed graphite in water, the monolayer flakes form a single sheet and create strong bonds. These sheets, called graphene oxide paper, have a measured tensile modulus of 32 GPa.^[209] The chemical property of graphite oxide is related to the functional groups attached to graphene sheets. These can change the polymerization pathway and similar chemical processes.^[210] Graphene oxide flakes in polymers display enhanced photo-conducting properties.^[211] Graphene is normally hydrophobic and impermeable to all gases and liquids (vacuum-tight). However, when formed into graphene oxide-based capillary membrane, both liquid water and water vapor flow through as quickly as if the membrane was not present.^[212]

Chemical modification

Photograph of single-layer graphene oxide undergoing high temperature chemical treatment, resulting in sheet folding and loss of carboxylic functionality, or through room temperature carbodiimide treatment, collapsing into star-like clusters.

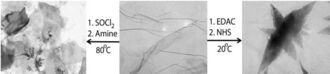
Soluble fragments of graphene can be prepared in the laboratory^[213] through chemical modification of graphite. First, microcrystalline graphite is treated with an acidic mixture of sulfuric acid and nitric acid. A series of oxidation and exfoliation steps produce small graphene plates with carboxyl groups at their edges. These are converted to acid chloride groups by treatment with thionyl chloride; next, they are converted to the corresponding graphene amide via treatment with octadecylamine. The resulting material (circular graphene layers of 5.3 Å or 5.3×10⁻¹⁰ m thickness) is soluble in tetrahydrofuran, tetrachloromethane and dichloroethane.

Refluxing single-layer graphene oxide (SLGO) in solvents leads to size reduction and folding of individual sheets as well as loss of carboxylic group functionality, by up to 20%, indicating thermal instabilities of SLGO sheets dependent on their preparation methodology. When using thionyl chloride, acyl chloride groups result, which can then form aliphatic and aromatic amides with a reactivity conversion of around 70–80%.

Boehm titration results for various chemical reactions of single-layer graphene oxide, which reveal reactivity of the carboxylic groups and the resultant stability of the SLGO sheets after treatment.

Hydrazine reflux is commonly used for reducing SLGO to SLG(R), but titrations show that only around 20–30% of the carboxylic groups are lost, leaving a significant number available for chemical attachment. Analysis of SLG(R) generated by this route reveals that the system is unstable and using a room temperature stirring with HCl (< 1.0 M) leads to around 60% loss of COOH functionality. Room temperature treatment of SLGO with carbodiimides leads to the collapse of the individual sheets into star-like clusters that exhibited poor subsequent reactivity with amines (c. 3–5% conversion of the intermediate to the final amide).^[214] It is apparent that conventional chemical treatment of carboxylic groups on SLGO generates morphological changes of individual sheets that leads to a reduction in chemical reactivity, which may potentially limit their use in composite synthesis. Therefore, chemical reactions types have been explored. SLGO has also been grafted with polyallylamine, cross-linked through epoxy groups. When filtered into graphene oxide paper, these composites exhibit increased stiffness and strength relative to unmodified graphene oxide paper.^[215]

Full hydrogenation from both sides of graphene sheet results in graphane, but partial hydrogenation leads to hydrogenated graphene.^[216] Similarly, both-side fluorination of graphene (or chemical and mechanical exfoliation of graphite fluoride) leads to fluorographene (graphene fluoride),^[217] while partial fluorination (generally halogenation) provides fluorinated (halogenated) graphene.

Graphene ligand/complex

Graphene can be a ligand to coordinate metals and metal ions by introducing functional groups. Structures of graphene ligands are similar to e.g. metal-porphyrin complex, metal-phthalocyanine complex, and metal-phenanthroline complex. Copper and nickel ions can be coordinated with graphene ligands.^[218][219]

Graphene fiber

In 2011, researchers reported a novel yet simple approach to fabricate graphene fibers from chemical vapor deposition grown graphene films.^[220] The method was scalable and controllable, delivering tunable morphology and pore structure by controlling the evaporation of solvents with suitable surface tension. Flexible all-solid-state supercapacitors based on this graphene fibers were demonstrated in 2013.^[221]

In 2015 intercalating small graphene fragments into the gaps formed by larger, coiled graphene sheets, after annealing provided pathways for conduction, while the fragments helped reinforce the fibers. The resulting fibers offered better thermal and electrical conductivity and mechanical strength. Thermal conductivity reached 1,290 W/m/K (1,290 watts per metre per kelvin), while tensile strength reached 1,080 MPa (157,000 psi).^[222]

In 2016, Kilometer-scale continuous graphene fibers with outstanding mechanical properties and excellent electrical conductivity are produced by high-throughput wet-spinning of graphene oxide liquid crystals followed by graphitization through a full-scale synergetic defect-engineering strategy.^[223] The graphene fibers with superior performances promise wide applications in functional textiles, lightweight motors, microelectronic devices, etc.

Tsinghua University in Beijing, led by Wei Fei of the Department of Chemical Engineering, claims to be able to create a carbon nanotube fibre which has a tensile strength of 80 GPa (12,000,000 psi).^[224]

3D graphene

In 2013, a three-dimensional honeycomb of hexagonally arranged carbon was termed 3D graphene, and self-supporting 3D graphene was also produced.^[225] 3D structures of graphene can be fabricated by using either CVD or solution based methods. A 2016 review by Khurram and Xu et al. provided a summary of then-state-of-the-art techniques for fabrication of the 3D structure of graphene and other related two-dimensional materials.^[226] In 2013, researchers at Stony Brook University reported a novel radical-initiated crosslinking method to fabricate porous 3D free-standing architectures of graphene and carbon nanotubes using nanomaterials as building blocks without any polymer matrix as support.^[227] These 3D graphene (all-carbon) scaffolds/foams have applications in several fields such as energy storage, filtration, thermal management and biomedical devices and implants.^[226][228]

Box-shaped graphene (BSG) nanostructure appearing after mechanical cleavage of pyrolytic graphite was reported in 2016.^[229] The discovered nanostructure is a multilayer system of parallel hollow nanochannels located along the surface and having quadrangular cross-section. The thickness of the channel walls is approximately equal to 1 nm. Potential fields of BSG application include: ultra-sensitive detectors, high-performance catalytic cells, nanochannels for DNA sequencing and manipulation, high-performance heat sinking surfaces, rechargeable batteries of enhanced performance, nanomechanical resonators, electron multiplication channels in emission nanoelectronic devices, high-capacity sorbents for safe hydrogen storage.

Three dimensional bilayer graphene has also been reported.^[230][231]

Pillared graphene

Main page: Chemistry:Pillared graphene

Pillared graphene is a hybrid carbon, structure consisting of an oriented array of carbon nanotubes connected at each end to a sheet of graphene. It was first described theoretically by George Froudakis and colleagues of the University of Crete in Greece in 2008. Pillared graphene has not yet been synthesised in the laboratory, but it has been suggested that it may have useful electronic properties, or as a hydrogen storage material.

Reinforced graphene

Graphene reinforced with embedded carbon nanotube reinforcing bars ("rebar") is easier to manipulate, while improving the electrical and mechanical qualities of both materials.^[232][233]

Functionalized single- or multiwalled carbon nanotubes are spin-coated on copper foils and then heated and cooled, using the nanotubes themselves as the carbon source. Under heating, the functional carbon groups decompose into graphene, while the nanotubes partially split and form in-plane covalent bonds with the graphene, adding strength. π–π stacking domains add more strength. The nanotubes can overlap, making the material a better conductor than standard CVD-grown graphene. The nanotubes effectively bridge the grain boundaries found in conventional graphene. The technique eliminates the traces of substrate on which later-separated sheets were deposited using epitaxy.^[232]

Stacks of a few layers have been proposed as a cost-effective and physically flexible replacement for indium tin oxide (ITO) used in displays and photovoltaic cells.^[232]

Moulded graphene

In 2015, researchers from the University of Illinois at Urbana-Champaign (UIUC) developed a new approach for forming 3D shapes from flat, 2D sheets of graphene.^[234] A film of graphene that had been soaked in solvent to make it swell and become malleable was overlaid on an underlying substrate "former". The solvent evaporated over time, leaving behind a layer of graphene that had taken on the shape of the underlying structure. In this way they were able to produce a range of relatively intricate micro-structured shapes.^[235] Features vary from 3.5 to 50 μm. Pure graphene and gold-decorated graphene were each successfully integrated with the substrate.^[236]

Graphene aerogel

An aerogel made of graphene layers separated by carbon nanotubes was measured at 0.16 milligrams per cubic centimeter. A solution of graphene and carbon nanotubes in a mold is freeze dried to dehydrate the solution, leaving the aerogel. The material has superior elasticity and absorption. It can recover completely after more than 90% compression, and absorb up to 900 times its weight in oil, at a rate of 68.8 grams per second.^[237]

Graphene nanocoil

In 2015 a coiled form of graphene was discovered in graphitic carbon (coal). The spiraling effect is produced by defects in the material's hexagonal grid that causes it to spiral along its edge, mimicking a Riemann surface, with the graphene surface approximately perpendicular to the axis. When voltage is applied to such a coil, current flows around the spiral, producing a magnetic field. The phenomenon applies to spirals with either zigzag or armchair patterns, although with different current distributions. Computer simulations indicated that a conventional spiral inductor of 205 microns in diameter could be matched by a nanocoil just 70 nanometers wide, with a field strength reaching as much as 1 tesla.^[238]

The nano-solenoids analyzed through computer models at Rice should be capable of producing powerful magnetic fields of about 1 tesla, about the same as the coils found in typical loudspeakers, according to Yakobson and his team – and about the same field strength as some MRI machines. They found the magnetic field would be strongest in the hollow, nanometer-wide cavity at the spiral's center.^[238]

A solenoid made with such a coil behaves as a quantum conductor whose current distribution between the core and exterior varies with applied voltage, resulting in nonlinear inductance.^[239]

Crumpled graphene

In 2016, Brown University introduced a method for 'crumpling' graphene, adding wrinkles to the material on a nanoscale. This was achieved by depositing layers of graphene oxide onto a shrink film, then shrunken, with the film dissolved before being shrunken again on another sheet of film. The crumpled graphene became superhydrophobic, and, when used as a battery electrode, the material was shown to have as much as a 400% increase in electrochemical current density.^[240][241]

5. Production

Main page: Chemistry:Graphene production techniques

A rapidly increasing list of production techniques have been developed to enable graphene's use in commercial applications.^[242]

Isolated 2D crystals cannot be grown via chemical synthesis beyond small sizes even in principle, because the rapid growth of phonon density with increasing lateral size forces 2D crystallites to bend into the third dimension. In all cases, graphene must bond to a substrate to retain its two-dimensional shape.^[19]

Small graphene structures, such as graphene quantum dots and nanoribbons, can be produced by "bottom up" methods that assemble the lattice from organic molecule monomers (e. g. citric acid, glucose). "Top down" methods, on the other hand, cut bulk graphite and graphene materials with strong chemicals (e. g. mixed acids).

Mechanical

Mechanical exfoliation

Geim and Novoselov initially used adhesive tape to pull graphene sheets away from graphite. Achieving single layers typically requires multiple exfoliation steps. After exfoliation the flakes are deposited on a silicon wafer. Crystallites larger than 1 mm and visible to the naked eye can be obtained.^[243]

As of 2014, exfoliation produced graphene with the lowest number of defects and highest electron mobility.^[244]

Alternatively a sharp single-crystal diamond wedge penetrates onto the graphite source to cleave layers.^[245]

In 2014 defect-free, unoxidized graphene-containing liquids were made from graphite using mixers that produce local shear rates greater than 10×10⁴.^[246][247]

Shear exfoliation is another method which by using rotor-stator mixer the scalable production of the defect-free Graphene has become possible ^[248] It has been shown that, as turbulence is not necessary for mechanical exfoliation,^[249] low speed ball milling is shown to be effective in the production of High-Yield and water-soluble graphene.

Ultrasonic exfoliation

Dispersing graphite in a liquid medium can produce graphene by sonication followed by centrifugation,^[250][251] producing concentrations 2.1 mg/ml in N-methylpyrrolidone.^[252] Using a suitable ionic liquid as the dispersing liquid medium produced concentrations of 5.33 mg/ml.^[253] Restacking is an issue with this technique.

Adding a surfactant to a solvent prior to sonication prevents restacking by adsorbing to the graphene's surface. This produces a higher graphene concentration, but removing the surfactant requires chemical treatments.

Sonicating graphite at the interface of two immiscible liquids, most notably heptane and water, produced macro-scale graphene films. The graphene sheets are adsorbed to the high energy interface between the materials and are kept from restacking. The sheets are up to about 95% transparent and conductive.^[254]

With definite cleavage parameters, the box-shaped graphene (BSG) nanostructure can be prepared on graphite crystal.^[229]

Splitting monolayer carbon

Nanotube slicing

Graphene can be created by opening carbon nanotubes by cutting or etching.^[255] In one such method multi-walled carbon nanotubes are cut open in solution by action of potassium permanganate and sulfuric acid.^[256][257]

In 2014, carbon nanotube-reinforced graphene was made via spin coating and annealing functionalized carbon nanotubes.^[232]

Fullerene splitting

Another approach sprays buckyballs at supersonic speeds onto a substrate. The balls cracked open upon impact, and the resulting unzipped cages then bond together to form a graphene film.^[258]

Chemical

Graphite oxide reduction

P. Boehm reported producing monolayer flakes of reduced graphene oxide in 1962.^[259][260] Rapid heating of graphite oxide and exfoliation yields highly dispersed carbon powder with a few percent of graphene flakes.

Another method is reduction of graphite oxide monolayer films, e.g. by hydrazine with annealing in argon/hydrogen with an almost intact carbon framework that allows efficient removal of functional groups. Measured charge carrier mobility exceeded 1000 cm/Vs (10m/Vs).^[261]

Burning a graphite oxide coated DVD produced a conductive graphene film (1738 siemens per meter) and specific surface area (1520 square meters per gram) that was highly resistant and malleable.^[262]

A dispersed reduced graphene oxide suspension was synthesized in water by a hydrothermal dehydration method without using any surfactant. The approach is facile, industrially applicable, environmentally friendly and cost effective. Viscosity measurements confirmed that the graphene colloidal suspension (Graphene nanofluid) exhibit Newtonian behavior, with the viscosity showing close resemblance to that of water.^[263]

Molten salts

Graphite particles can be corroded in molten salts to form a variety of carbon nanostructures including graphene.^[264] Hydrogen cations, dissolved in molten lithium chloride, can be discharged on cathodically polarized graphite rods, which then intercalate, peeling graphene sheets. The graphene nanosheets produced displayed a single-crystalline structure with a lateral size of several hundred nanometers and a high degree of crystallinity and thermal stability.^[265]

Electrochemical synthesis

Electrochemical synthesis can exfoliate graphene. Varying a pulsed voltage controls thickness, flake area, number of defects and affects its properties. The process begins by bathing the graphite in a solvent for intercalation. The process can be tracked by monitoring the solution's transparency with an LED and photodiode. ^[266][267]

Hydrothermal self-assembly

Graphene has been prepared by using a sugar (e.g. glucose, sugar, fructose, etc.) This substrate-free "bottom-up" synthesis is safer, simpler and more environmentally friendly than exfoliation. The method can control thickness, ranging from monolayer to multilayers, which is known as "Tang-Lau Method".^{[268][269][270][271]}

Sodium ethoxide pyrolysis

Gram-quantities were produced by the reaction of ethanol with sodium metal, followed by pyrolysis and washing with water.^[272]

Microwave-assisted oxidation

In 2012, microwave energy was reported to directly synthesize graphene in one step.^[273] This approach avoids use of potassium permanganate in the reaction mixture. It was also reported that by microwave radiation assistance, graphene oxide with or without holes can be synthesized by controlling microwave time.^[274] Microwave heating can dramatically shorten the reaction time from days to seconds.

Graphene can also be made by microwave assisted hydrothermal pyrolysis.^[205][206]

Thermal decomposition of silicon carbide

Heating silicon carbide (SiC) to high temperatures (1100 °C) under low pressures (c. 10⁻⁶ torr, or 10⁻⁴ Pa) reduces it to graphene.^{[89][90][91][92][93][275]}

Chemical vapor deposition

Epitaxy

Epitaxial graphene growth on silicon carbide is wafer-scale technique to produce graphene. Epitaxial graphene may be coupled to surfaces weakly enough (by the active valence electrons that create Van der Waals forces) to retain the two dimensional electronic band structure of isolated graphene.^[276]

A normal silicon wafer coated with a layer of germanium (Ge) dipped in dilute hydrofluoric acid strips the naturally forming germanium oxide groups, creating hydrogen-terminated germanium. CVD can coat that with graphene.^[277][278]

The direct synthesis of graphene on insulator TiO₂ with high-dielectric-constant (high-κ). A two-step CVD process is shown to grow graphene directly on TiO₂ crystals or exfoliated TiO₂ nanosheets without using any metal catalyst.^[279]

Metal substrates

CVD graphene can be grown on metal substrates including ruthenium,^[280] iridium,^[281] nickel^[282] and copper.^[283][284]

Roll-to-roll

In 2014 a two-step roll-to-roll manufacturing process was announced. The first roll-to-roll step produces the graphene via chemical vapor deposition. The second step binds the graphene to a substrate.^[285][286]

Large-area Raman mapping of CVD graphene on deposited Cu thin film on 150 mm SiO₂/Si wafers reveals >95% monolayer continuity and an average value of ~2.62 for I_2D/I_G. The scale bar is 200 μm.

Cold wall

Growing graphene in an industrial resistive-heating cold wall CVD system was claimed to produce graphene 100 times faster than conventional CVD systems, cut costs by 99% and produce material with enhanced electronic qualities.^[287][288]

Wafer scale CVD graphene

CVD graphene is scalable and has been grown on deposited Cu thin film catalyst on 100 to 300 mm standard Si/SiO₂ wafers^{[289][290][291]} on an Axitron Black Magic system. Monolayer graphene coverage of >95% is achieved on 100 to 300 mm wafer substrates with negligible defects, confirmed by extensive Raman mapping.^[290][291]

Solvent interface trapping method (SITM)

Reported by a group led by D. H. Adamson, graphene can be produced from natural graphite while preserving the integrity of the sheets using solvent interface trapping method (SITM). SITM use a high energy interface, such as oil and water, to exfoliate graphite to graphene. Stacked graphite delaminates, or spreads, at the oil/water interface to produce few-layer graphene in a thermodynamically favorable process in much the same way as small molecule surfactants spread to minimize the interfacial energy. In this way, graphene behaves like a 2D surfactant.^{[292][293][294]} SITM has been reported for a variety of applications such conductive polymer-graphene foams,^{[295][296][297][298]} conductive polymer-graphene microspheres,^[299] conductive thin films^[300] and conductive inks.^[301]

Carbon dioxide reduction

A highly exothermic reaction combusts magnesium in an oxidation–reduction reaction with carbon dioxide, producing carbon nanoparticles including graphene and fullerenes.^[302]

Supersonic spray

Supersonic acceleration of droplets through a Laval nozzle was used to deposit reduced graphene-oxide on a substrate. The energy of the impact rearranges that carbon atoms into flawless graphene.^[303][304]

Laser

In 2014, a CO₂ infrared laser was used to produce patterned porous three-dimensional laser-induced graphene (LIG) film networks from commercial polymer films. The resulting material exhibits high electrical conductivity and surface area. The laser induction process is compatible with roll-to-roll manufacturing processes.^[305] A similar material, laser-induced graphene fibers (LIGF), was reported in 2018.^[306]

Flash Joule heating

In 2019, flash Joule heating (transient high-temperature electrothermal heating) was discovered to be a method to synthesize turbostratic graphene in bulk powder form. The method involves electrothermally converting various carbon sources, such as carbon black, coal, and food waste into micron-scale flakes of graphene.^[196][307] More recent works demonstrated the use of mixed plastic waste, waste rubber tires, and pyrolysis ash as carbon feedstocks.^{[308][309][310]} The graphenization process is kinetically controlled, and the energy dose is chosen to preserve the carbon in its graphenic state (excessive energy input leads to subsequent graphitization through annealing).

Ion implantation

Accelerating carbon ions inside an electrical field into a semiconductor made of thin nickel films on a substrate of SiO₂/Si, creates a wafer-scale (4 inches (100 mm)) wrinkle/tear/residue-free graphene layer at a relatively low temperature of 500 °C.^[311][312]

CMOS-compatible graphene

Integration of graphene in the widely employed CMOS fabrication process demands its transfer-free direct synthesis on dielectric substrates at temperatures below 500 °C. At the IEDM 2018, researchers from University of California, Santa Barbara, demonstrated a novel CMOS-compatible graphene synthesis process at 300 °C suitable for back-end-of-line (BEOL) applications.^{[313][314][315]} The process involves pressure-assisted solid-state diffusion of carbon through a thin-film of metal catalyst. The synthesized large-area graphene films were shown to exhibit high-quality (via Raman characterization) and similar resistivity values when compared with high-temperature CVD synthesized graphene films of same cross-section down to widths of 20 nm.

6. Simulation

In addition to experimental investigation of graphene and graphene-based devices, their numerical modeling and simulation have been an important research topic. The Kubo formula provides an analytic expression for the graphene's conductivity and shows that it is a function of several physical parameters including wavelength, temperature, and chemical potential.^[316] Moreover, a surface conductivity model, which describes graphene as an infinitesimally thin (two sided) sheet with a local and isotropic conductivity, has been proposed. This model permits derivation of analytical expressions for the electromagnetic field in the presence of a graphene sheet in terms of a dyadic Green function (represented using Sommerfeld integrals) and exciting electric current.^[317] Even though these analytical models and methods can provide results for several canonical problems for benchmarking purposes, many practical problems involving graphene, such as design of arbitrarily shaped electromagnetic devices, are analytically intractable. With the recent advances in the field of computational electromagnetics (CEM), various accurate and efficient numerical methods have become available for analysis of electromagnetic field/wave interactions on graphene sheets and/or graphene-based devices. A comprehensive summary of computational tools developed for analyzing graphene-based devices/systems is proposed.^[318]

7. Graphene Analogs

Graphene analogs^[319] (also referred to as "artificial graphene") are two-dimensional systems which exhibit similar properties to graphene. Graphene analogs are studied intensively since the discovery of graphene in 2004. People try to develop systems in which the physics is easier to observe and to manipulate than in graphene. In those systems, electrons are not always the particles which are used. They might be optical photons,^[320] microwave photons,^[321] plasmons,^[322] microcavity polaritons,^[323] or even atoms.^[324] Also, the honeycomb structure in which those particles evolve can be of a different nature than carbon atoms in graphene. It can be, respectively, a photonic crystal, an array of metallic rods, metallic nanoparticles, a lattice of coupled microcavities, or an optical lattice.

8. Applications

Main page: Chemistry:Potential applications of graphene

(a) The typical structure of a touch sensor in a touch panel. (Image courtesy of Synaptics, Incorporated.) (b) An actual example of 2D Carbon Graphene Material Co.,Ltd's graphene transparent conductor-based touchscreen that is employed in (c) a commercial smartphone.

Graphene is a transparent and flexible conductor that holds great promise for various material/device applications, including solar cells,^[325] light-emitting diodes (LED), integrated photonic circuit devices,^[326][327] touch panels, and smart windows or phones.^[328] Smartphone products with graphene touch screens are already on the market.^[329]

In 2013, Head announced their new range of graphene tennis racquets.^[330]

As of 2015, there is one product available for commercial use: a graphene-infused printer powder.^[331] Many other uses for graphene have been proposed or are under development, in areas including electronics, biological engineering, filtration, lightweight/strong composite materials, photovoltaics and energy storage.^[226][332] Graphene is often produced as a powder and as a dispersion in a polymer matrix. This dispersion is supposedly suitable for advanced composites,^[333][334] paints and coatings, lubricants, oils and functional fluids, capacitors and batteries, thermal management applications, display materials and packaging, solar cells, inks and 3D-printers' materials, and barriers and films.^[335]

On August 2, 2016, BAC's new Mono model is said to be made out of graphene as a first of both a street-legal track car and a production car.^[336]

In January 2018, graphene based spiral inductors exploiting kinetic inductance at room temperature were first demonstrated at the University of California, Santa Barbara, led by Kaustav Banerjee. These inductors were predicted to allow significant miniaturization in radio-frequency integrated circuit applications.^{[337][338][339]}

The potential of epitaxial graphene on SiC for metrology has been shown since 2010, displaying quantum Hall resistance quantization accuracy of three parts per billion in monolayer epitaxial graphene. Over the years precisions of parts-per-trillion in the Hall resistance quantization and giant quantum Hall plateaus have been demonstrated. Developments in encapsulation and doping of epitaxial graphene have led to the commercialisation of epitaxial graphene quantum resistance standards.^[340]

9. Toxicity

One review on graphene toxicity published in 2016 by Lalwani et al. summarizes the in vitro, in vivo, antimicrobial and environmental effects and highlights the various mechanisms of graphene toxicity.^[341] Another review published in 2016 by Ou et al. focussed on graphene-family nanomaterials (GFNs) and revealed several typical mechanisms such as physical destruction, oxidative stress, DNA damage, inflammatory response, apoptosis, autophagy, and necrosis.^[342]

A 2020 study showed that the toxicity of graphene is dependent on several factors such as shape, size, purity, post-production processing steps, oxidative state, functional groups, dispersion state, synthesis methods, route and dose of administration, and exposure times.^[343]

In 2014 research at Stony Brook University showed that graphene nanoribbons, graphene nanoplatelets and graphene nano–onions are non-toxic at concentrations up to 50 μg/ml. These nanoparticles do not alter the differentiation of human bone marrow stem cells towards osteoblasts (bone) or adipocytes (fat) suggesting that at low doses graphene nanoparticles are safe for biomedical applications.^[344] In 2013 research at Brown University found that 10 μm few-layered graphene flakes are able to pierce cell membranes in solution. They were observed to enter initially via sharp and jagged points, allowing graphene to be internalized in the cell. The physiological effects of this remain unknown, and this remains a relatively unexplored field.^[345][346]

This entry is adapted from the peer-reviewed paper 10.3390/en13184867