Improving Dust Collector Efficiency for Pneumatic Conveying: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Engineering, Mechanical
Contributor:
Philippe Beaulac

Dust collecting systems are composed of three main sub-systems: figure 3 shows the main components of a dust collecting system. A dust collection system removes the dust contents of an industrial environment to provide a comfortable work environment and meet safety and health regulations. The system takes the dust particles and carries them outside for disposal or reuse possibilities.

  • fluid mechanics
  • pneumatic conveying
  • multiphase flows
  • dust collector
  • industrial control
  • energy efficiency

1. Introduction

According to the Energy Information Administration of the US Department of Energy[1][2], and summarized in Table 1, the industrial sector consumes 32.53% of the overall energy consumption worldwide.
Table 1. Energy consumption by sector, 2019[1].
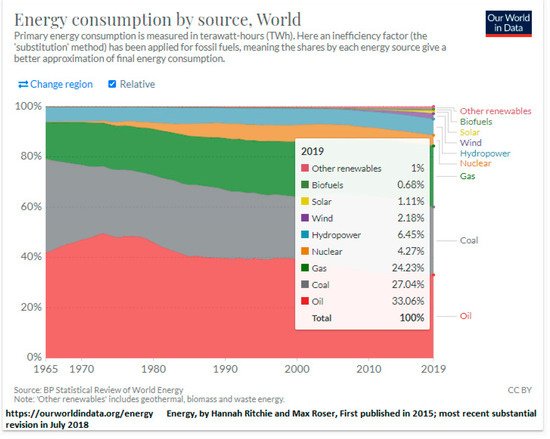
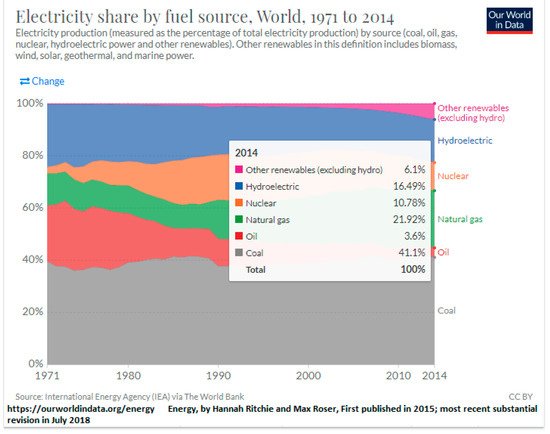
Sector Petawatt-Hours Percentage
Residential 20.98 20.98
Commercial 17.94 17.94
Industrial 95.75 32.53
Transportation 84.02 28.55
Total 272.43 100
It does not only represent the electricity consumption, but with such a high proportion, it becomes highly justifiable to put efforts into increasing the energy efficiency of industrial applications. These efforts should be prioritized in areas where the energy production emits high concentrations of greenhouse gas (GHG).
Furthermore, extensive research on energy consumption[3] has outlined figures on energy consumption and global electricity production by source. From these figures, we can notice that fossil fuel consumption represents 84.33% of all energy consumption in the world as of 2019 (Figure 1) and that 67.03% of global electricity production comes from fossil fuels (Figure 2).
Energies 15 00916 g001 550
Figure 1. Energy consumption in the world, 2019.
Energies 15 00916 g002 550
Figure 2. Global electricity production distribution.
These high percentages and the increasingly pressing need to diminish our GHG emissions more than justify efforts to optimize industrial energy consumptions through better accuracy of their control strategies. Other incentives become more and more pressing as climate changes are widely felt. These take the form of regulations such as taxes, subsidies, tradable emission permits, and green certificates, as outlined by Bunse[4].
To improve the energy efficiency of an industrial system, one possible avenue is by better controlling its energy consumption by optimizing it according to the production needs. The operating costs of industrial systems are directly associated with the electrical energy consumed.
Many industrial applications consume more energy than required to respond to demands. One can refer to dust collection systems and compressed air systems that almost always show leaks[5]. These systems tend to run at 100% capacity for the duration of the production periods.
This surplus of consumption can seem low, if regarded per industrial system, but becomes considerably high when considering the whole factory, with all its systems. If a control strategy allows for the reduction of the gap between input and output, the benefits can only be increased.

2. Dust Collector System Overview

Dust collecting systems are composed of three main sub-systems:
  • The cyclone with its centrifugal pump (fan) and filter units (bags)
  • The dust evacuation sub-system (airlock and dust disposal)
  • The dust collection and transport circuits (cut-off valves (blast gates) and ducting)
Figure 3 shows the main components of a dust collecting system.
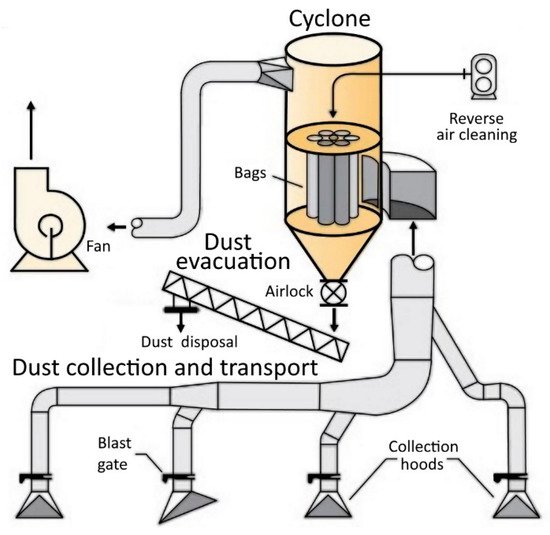
Energies 15 00916 g003 550
Figure 3. Schematic of a dust collection system.
A dust collection system removes the dust contents of an industrial environment to provide a comfortable work environment and meet safety and health regulations. The system takes the dust particles and carries them outside for disposal or reuse possibilities.
The system has a power unit that develops the necessary work for the collection and transport of the particles and the separation of the dust particles from their carrying fluid, usually air. This power unit is the electric motor and fan attached to the cyclone, which separates the two phases of the flow, i.e., (i) the dust and the transporting fluid, and; (ii) the air. This power unit utilizes a ducting network to transport the dust from the collection points throughout the plant. When designing the ducting network, careful considerations must be taken to achieve a high-efficiency pneumatic conveying of the dust particles. Modern systems tend to use controlling strategies to save energy by closing specific areas of the ducting circuit that do not require dust removal. One of these systems consists of gate valves, operated by pneumatic energy, which close the ducts at strategically selected points in the circuit. This efficiency strategy is coupled with a variable frequency drive control that can reduce the motor’s speed to meet the required dust collection needs.
The dust evacuation sub-system comprises a rotating airlock valve that transfers the dust particles from the dust collector to the dust disposal mechanism and isolates the evacuation duct from the cyclone chamber. The dust disposal mechanism serves to evacuate the dust particles to a container, which can be taken away from the factory to disposal sites or alternate users. Since this sub-system has limited influence on the overall performance of the dust collection system, its details will be omitted in this study. Emphasis will be put on the cyclone unit and the ducting circuit. The performance of the dust collecting system relies on the proper transport of the dust in the collecting ducts and the adequate separation of the dust from the transporting medium, in our case, air. The energy-consuming component of a dust collection system is the electric motor that implements the rotation conditions for the centrifugal pump, the fan, the most critical element of the system, producing the airflow necessary to transport the dust particles to the dust collector. The efficiency and energy consumption of the electric motor are directly linked to the behavior of the upstream components, the ducting, and the collection hoods. Unfortunately, typical dust collector systems do not present the means to adjust the electric motor’s velocity. Dust collector manufacturers offer the option of adding a variable frequency drive, which can significantly improve the system’s overall efficiency.
The influential parameters for proper dust collection are the velocities of the air flow in the ducts, directly dependent on the differential pressures present in the various locations in the system. Other parameters that could influence the performance of the system are the density of dust present in the ducts, the shape and size of the dust particles, the temperature and the humidity of the flow[6][7]. According to Clarke’s study[6], there is a 0.16 m/s difference in the fluidization velocity of sawdust particles containing moisture ranging from 8% to 82%, which appears to present minimal effect. Kunii’s Fluidization Engineering manual[7] points out the influence of the void fraction between particles on the fluidization velocities. This critical parameter of the flow increases by up to 8% for temperatures up to 500 ℃ for fine particles, but is unaffected for coarse particles, which is the case for sawdust particles. These two last parameters have a significantly smaller influence on the performance of the system than the rest of the enumerated parameters, so they will be set aside for the scope of this study.
Dust collectors and pneumatic conveying have been developed and used in industrial transport applications for well over 100 years. The technology emerged from the invention of the Roots blower (Figure 4), which was first tried in 1859 by the Roots brothers in the U.S.[8], and it is still widely used in modern pneumatic conveying applications, although it has been continually tested and upgraded into what we know of it today.
Energies 15 00916 g004 550
Figure 4. Roots blower[9].
The two main technologies used by this industrial application: the cyclone of the dust collector itself,  serves to separate the dust from the airflow, and the pneumatic conveying circuit, which serves to transport the particles to the dust collector.

3. Cyclones

The cyclone is an integral part of the power source of the dust collecting system. It serves a general purpose of separating the two phases of the flow: the solid phase is deposited in the bottom to be later evacuated from the system, and the gas phase is recirculated back into the system, or simply exhausted to the environment during periods of higher ambient temperatures. Obviously, the recirculation of the exhaust air to the plant in colder periods allows for the retention of a portion of the thermal charge of the air for heating efficiency purposes.
A cyclone is generally of cylindrical shape, with a cone at its bottom to collect the solid phase. The dimensions of the cyclone are established according to the performance desired and the type of application it will be subjected to, as explained by Leith[10]. The dimensioning criteria are the height and width of the inlet conduit, the ratio of the heights of the cylindrical and conical parts, and ratios in relation to the overall diameter of the cyclone.
The multiphase flow enters the cyclone and forms a vortex that forces the solid particles to adhere to the inner walls of the cylindrical part of the cyclone. When the particles are subjected to boundary layer conditions, they fall to the bottom of the conical part to be evacuated out of the cyclone.
The overall efficiency of the cyclone is mainly given by its ability to separate the two phases of the flow, as defined by Azadi[11]: it is referred to as the separation rate. It is expressed via the rate of settling of particles according to their size.

4. Pneumatic conveying

The principle of pneumatic conveying rests on the transport properties of a fluid, usually air, to efficiently carry bulk products from a point of delivery to a point of transformation. Setting aside the cyclone and filtering system which serve to separate the solid phase from the fluid phase, the pneumatic conveying system is composed of a turbine, blower or fan, and a network of ducts. The turbine produces the fluid movement, and the ducting directs the solids to the discharge point. This transport method is often preferred to mechanical conveyors because of its lower equipment costs and ease of maintenance[12].

The principle rests on the action of fluidization of beds of particles: a fluid flows through a packed bed of particles at sufficient velocities to loosen the particles and carry them in a particle-fluid mixture that behaves very much like a single-phased fluid[7][13]. The fluidization can be divided into distinct regimes. The first fluidization phase can be described as air being forced through a bed of particles causing a pressure drop across the bed. As the pressure drop increases, it becomes sufficient to support the particles in suspension in the air flow: this is the minimum fluidization velocity. If the air flow continues to increase, formation of bubbles occurs, in which the particles are carried. These bubbles will become slugs (or plugs) when the velocity continues to increase[14].

The design parameters that direct a particular pneumatic conveying system are imposed by the particles to be carried. According to Klinzing[12] it is important to consider the properties of the particles to be carried in the system, prior to its design:

  • Average particle size and size distribution
  • Percent of particles < 200 μm
  • Assessment of the characteristic of stickiness
  • Moisture content
  • True density and bulk density of the particles

The main element of the problem rests on the nature of the flow in the system. The charge on the system is directly proportional to the quantity of material to transport, but also pertains to the configuration of the ducting network and the surrounding conditions (temperature, humidity, atmospheric pressure).

Multiphase flows composed of a solid and a gas phase are primarily characterized by their solid particle contents. According to the volume fraction αs of the solid phase of the flow, it can be characterized as a dilute or dense flow.

The increase of particle density in the flow will affect the mode of transport by changing the flow pattern. Figure 5 shows sketches of the possible patterns of flow in ducts, adapted from Wen[15], established from observation of glass bead flows.

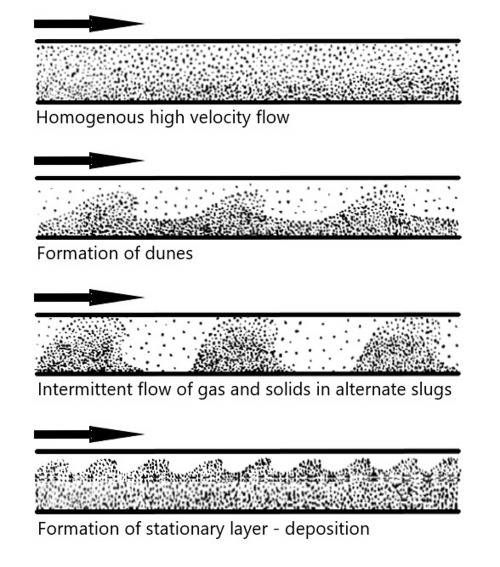
 Figure 5: flow patterns for glass beads[15]

The profiles shown in these flow patterns demonstrate the impact of the transport velocities on the overall performance of the system. When the velocity is sufficient to transport all the particles in the flow, the distribution of particles in the duct is homogenous and there is little deposition.

Manjula et al.[16] describe the difference in dilute and dense flows: in dilute multiphase flows, the bulk of the particles are transported by being suspended in the transporting gas; if the gas velocity is reduced, the flow of particles starts to display dune-like features or definite plugs of particles and most of the particles are no longer suspended in the transporting gas. This last situation describes a dense multiphase flow. From this description, one can readily assume that the effect of varying density will also affect the flow of particles.

As the density of particles increases or inversely as the velocity decreases, the flow starts to segregate into regions of higher density and the formation of dunes takes place. Further increase of the density will develop a slug flow and eventually the formation of a stationary layer of particles in the duct[15].

The relation between the pressure and the velocity can be associated with the density of particles in the flow. The behavior of pressure in a flow is similar to that of a potential difference in an electric circuit: the more there are resistances in the circuit, the bigger the potential difference, and similarly, the more there are resistances to the free flow of the fluid in the pipes, the higher the pressure differential[17].

A dilute particle phase will present very little resistance to the flow, hence low pressure buildup. And since the flow does not contain many particles, the velocity is maximum, being affected very little. Inversely, if the particle phase is dense, it means there are more particles to carry, hence more resistance to the flow, and higher pressure. In this case, the velocity is greatly affected by the dense particle phase. This is based on the principles of conservation of energy and explained by Thomson’s[18].

As illustrated in Figure 6, dense particle phase flows can present an accumulation of particles into plugs which can still be transported, provided that the system can produce enough power to meet the charge of particles.

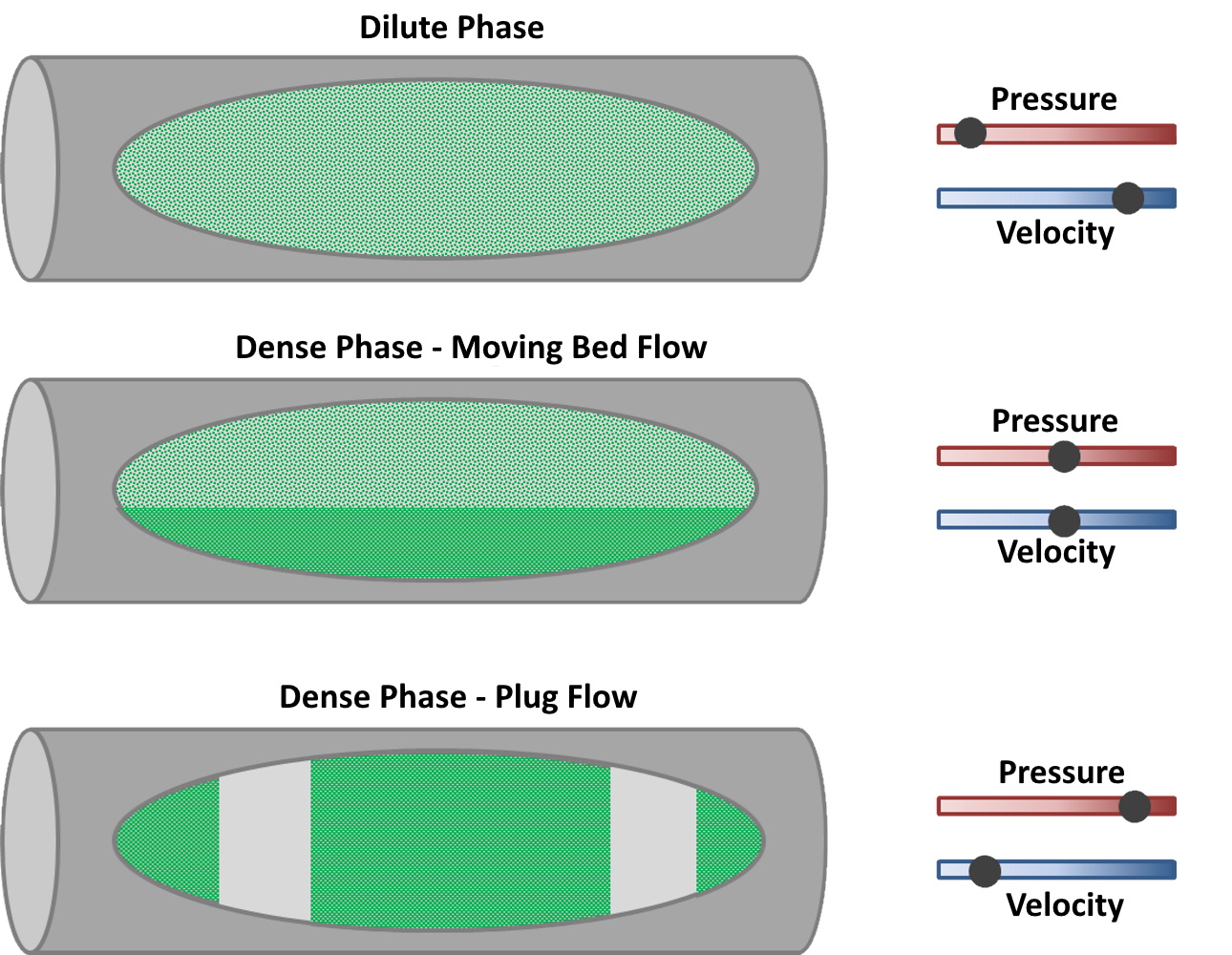
Figure 6: dilute vs dense phase flow[19]

To improve the efficiency of a dust collecting system, it becomes imperative to determine the type of flow that is optimal, in order to set our parameter standards to reach. In a study of the prediction modes of flow in pneumatic conveying systems, Jones and Williams[20] established that the optimal mode of flow is a dense particle phase flow, rather than a dilute phase flow. Dense particle flows can be distinguished between two classes: a fluidized dense phase which is characterized by a high air retention and low permeability, and a plug-type (or slug-type) flow for materials that de-aerates quickly and possesses a high permeability[20].

5. Multiphase viscous flow in ducts

A dust collecting system is composed of various ducting elements that direct the collected particles to the cyclone. The typical elements are the ducts themselves, with their respective shape, size and inner surface roughness. The rest of the elements are accessories that help to link together the network, such as elbows, junctions and transition pieces. Figure 7 shows a rendering of a typical dust collecting network.

 

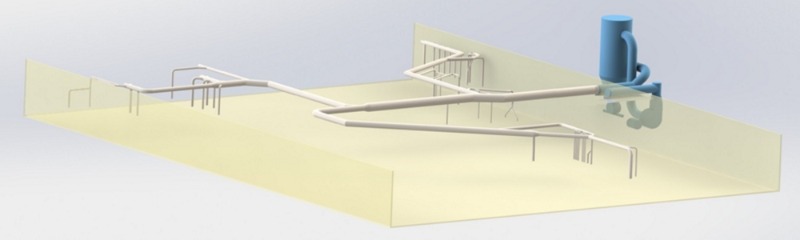
Figure 7: dust collecting network

The performance of the ducting network is characterized by its effects on the flow, hence the loss of transport power along the ducts. This loss is a function of the pressure drop in the ducting.

The pressure drop due to the fluid can be calculated from the following equation, where fD is the Darcy friction factor of the interior surface of the pipe.

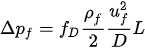where

Δp is in Pa

ρf is in kg/m3

uf is in m/s

L and D are in m

Many studies[21][22][23][24][25][26][27] were conducted to determine more precisely the friction factor according to the surface roughness of the piping used. According to many fluid mechanics manuals like White[28], the most widely used study is from Moody[29] which gave us the Moody chart for evaluating the friction factor of a single-phase flow in a pipe.

Any dust collecting system is basically composed of a typical matrix element of two pipes joining into one. Figure 8 shows this element of which the whole network can be drawn as a combination of many such elements. From this we can deduce that the principles of conservation of mass can be applied as per the following equation, and according to the Reynolds transport theorem.

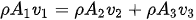
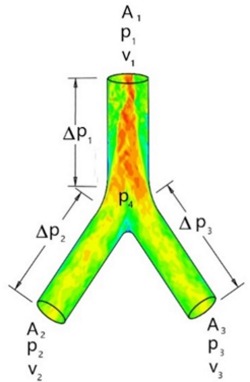Figure 8: typical mesh element

In a dust collecting system the entry volumes are at points 2 and 3, and the outlet volume is at point 1. This typical control volume can be used as the basis for the elaboration of the matrices that will be used to develop the model of the system. The model will render velocity profiles to maintain at each dust collection inlet to assure proper transport as to guaranty a dust free work environment for the surrounding workers. The velocity being a function of the pressure differential, the following expressions describe this relation.

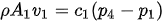
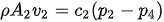
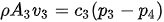
Since the density and the conduit areas are known and static, we can transfer these two parameters into the constants ci and the previous expression becomes

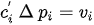
and a matrix system can be derived

We want to guaranty a sufficient transport velocity at each pickup inlet, so the matrices system will verify that

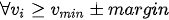
6. Conclusion

The influencing parameters which pertain to the cyclone are the inlet velocity and the pressure drop between the inlet and the outlet. The influencing parameters for the pneumatic transport of the particles, from their origin points to the cyclone are the velocities and pressure drops, but another parameter presents an influence, the density of the material being transported. All three parameters influence each other and need to be considered as such.

Multiphase flows in a ducting network can be analysed with a matrix and help us conclude that the velocities must be controlled in order to maintain a sufficient transport performance. Ultimately, we can evaluate the velocity vi at each moment, this velocity being the actual air-dust mixture velocity at the dust collector entry, hence in direct relation to the driving motor's speed, which is what we can control in such a system.

This entry is adapted from the peer-reviewed paper 10.3390/en15030916

References

  1. Total Energy . Total Energy. Retrieved 2022-2-25
  2. Conti, J.H., Paul; Diefenderfer, Jim; LaRose, Angelina; Turnure, James T.; Westfall, Lynn; International Energy outlook 2016. U.S. Energy Information Administration 2016, 1, 1, .
  3. Energy. Our World in Data . Energy. Retrieved 2022-2-25
  4. Bunse, K., et al.; Integrating energy efficiency performance in production management–gap analysis between industrial needs and scientific literature.. Journal of Cleaner Production 2011, 19, 667-679, .
  5. Kaya, D., et al.; Energy conservation in compressed-air systems. International Journal of Energy Research 2002, 26, 837-849, .
  6. Clarke, K.L., T. Pugsley, and G.A. Hill; Fluidization of moist sawdust in binary particle systems in a gas–solid fluidized bed. Chemical Engineering Science 2005, 60, 6909-6918, .
  7. Kunii, D.a.O.L.. Fluidization Engineering; M.I.T. Howard Brenner, Eds.; Butterworth-Heinemann: Stoneham, MA, USA, 1991; pp. 491.
  8. Klinzing, G.E.; Historical Review of Pneumatic Conveying. KONA Powder and Particle Journal 2018, 35, 150-159, .
  9. Twin Lobe High Pressure Blowers . Roots. Retrieved 2022-2-25
  10. Leith, D.a.D.M.; Cyclone performance and design. Atmospheric Environment 1973, 7, 527-549, .
  11. Azadi, M.; An analytical study of the effect of inlet velocity on the cyclone performance using mathematical models. Powder Technology 2012, 217, 121-127, .
  12. George E. Klinzing; A review of pneumatic conveying status, advances and projections. Powder Technology 2018, 333, 78-90, 10.1016/j.powtec.2018.04.012.
  13. Subramanian, R.S.; Flow through Packed and Fluidized Beds. Department of Chemical and Biomolecular Engineering Clarkson University 2002, 1, 1-6, .
  14. Gidaspow, D.. Multiphase Flow and Fluidization; United Kingdom Edition, Eds.; Academic Press: San Diedo, California, U.S., 1994; pp. 467.
  15. Chin-Yung Wen; H. P. Simons; Flow characteristics in horizontal fluidized solids transport. AIChE Journal 1959, 5, 263-267, 10.1002/aic.690050225.
  16. E.V.P.J. Manjula; W.K. Hiromi Ariyaratne; Chandana Ratnayake; Morten C. Melaaen; A review of CFD modelling studies on pneumatic conveying and challenges in modelling offshore drill cuttings transport. Powder Technology 2016, 305, 782-793, 10.1016/j.powtec.2016.10.026.
  17. Shrikant V. Dhodapkar; George E. Klinzing; Pressure fluctuations in pneumatic conveying systems. Powder Technology 1993, 74, 179-195, 10.1016/0032-5910(93)87010-l.
  18. Thomson, W.J.. Transport phenomena; Prentice Hall: Upper Saddle River, New Jersey, U.S., 2000; pp. 509.
  19. Are there different types of pneumatic conveying systems? . DE DIETRICH PROCESS SYSTEMS. Retrieved 2022-2-25
  20. Mark G. Jones; Kenneth Williams; Predicting the mode of flow in pneumatic conveying systems—A review. Particuology 2008, 6, 289-300, 10.1016/j.partic.2008.05.003.
  21. Chunbao Charles Xu; Jesse Zhu; PREDICTION OF THE MINIMUM FLUIDIZATION VELOCITY FOR FINE PARTICLES OF VARIOUS DEGREES OF COHESIVENESS. Chemical Engineering Communications 2008, 196, 499-517, 10.1080/00986440802483855.
  22. Ergun, S.; Fluid Flow Through Packed Columns. Chemical Engineering Progress 1952, 48, 89-94, .
  23. COLEBROOK, C.F., et al.; CORRESPONDENCE. TURBULENT FLOW IN PIPES, WITH PARTICULAR REFERENCE TO THE TRANSITION REGION BETWEEN THE SMOOTH AND ROUGH PIPE LAWS. (INCLUDES PLATES). Journal of the Institution of Civil Engineers 1939, 12, 393-422, .
  24. Fadi Z. Kamand; Hydraulic Friction Factors for Pipe Flow. Journal of Irrigation and Drainage Engineering 1988, 114, 311-323, 10.1061/(asce)0733-9437(1988)114:2(311).
  25. B. J. McKEON; C. J. Swanson; M. V. Zagarola; R. J. Donnelly; A. J. Smits; Friction factors for smooth pipe flow. Journal of Fluid Mechanics 2004, 511, 41-44, 10.1017/s0022112004009796.
  26. H. Herwig; D. Gloss; T. Wenterodt; A new approach to understanding and modelling the influence of wall roughness on friction factors for pipe and channel flows. Journal of Fluid Mechanics 2008, 613, 35-53, 10.1017/s0022112008003534.
  27. Kiijarvi, J.; Darcy friction factor formulae in turbulent pipe flow. Lunowa Fluid Mechanics Paper 2011, 110727, 1-11, .
  28. White, F.M.. Fluid Mechanics; McGraw-Hill: New-York, 2016; pp. 848.
  29. Moody, L.F.; Friction Factors for Pipe Flow. Transactions of the A.S.M.E. 1944, 1, 671-684, .
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
Video Production Service
Feedback