Concurrent Topology Optimization of Composite Plates: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects: Mechanics
Contributor:
Heng Zhang

Thin-walled composite plates have been widely used as structural components in various engineering applications to bear static and dynamic loads. The vibrations caused by the dynamic loads are transmitted to passengers and precision equipment, which reduces the crew’s comfort, affects normal operations, and shortens the service life of high-precision equipment. There is a rising demand to design optimal composites that have a superior combination of high stiffness and exceptional vibration mitigation capability. 

  • concurrent topology optimization
  • damping composite materials
  • dynamic compliance
  • homogenization
  • composite plates

1. Introduction

Thin-walled composite plates have been widely used as structural components in various engineering applications to bear static and dynamic loads. The vibrations caused by the dynamic loads are transmitted to passengers and precision equipment, which reduces the crew’s comfort, affects normal operations, and shortens the service life of high-precision equipment [1]. There is a rising demand to design optimal composites that have a superior combination of high stiffness and exceptional vibration mitigation capability. Over the past few decades, active and passive methods have been developed to improve the dynamic performance of composite structures [2][3][4][5]. Among these methods, incorporating a passive damping material layer into the base plates (i.e., free-layer [6] or constrained-layer [7][8]) is one of the most efficient, robust, and low-cost methods. Intrinsically, the vibration performance of the composite plates is determined by the properties of the damping materials and their topological arrangements on the base plates. Conventional design practices for damping composite architectures are focused on parameter analysis, in which only a few design variables are considered (i.e., the thickness or the size of the damping layer) [9][10]. However, these rely heavily on the designers’ intuition and it is hard to obtain the optimal configurations. These challenges are more notable when optimal microstructural damping configurations and macroscopic arrangements are simultaneously pursued.
Topology optimization (TO) [11][12] is a powerful inverse design technique that does not require predefined shapes. It can be used to generate a free-form optimal configuration that fulfills the functional requirements quantified by the objective functions and constraints. A series of TO methods have been developed to design damping composite structures, which can be broadly classified into two categories: one is to optimize the macrostructure layout of the damping material on the plates [13][14][15][16], while the other is focused on optimizing the composite architectures in microscale [17][18][19][20] using the homogenization method [21][22][23][24]. However, most existing works focus on either the macro- or micro-scale TO. Recent studies show that combining the macrostructure topology optimization with microscale composite material design can significantly improve structural performance. Zhu [25] proposed a concurrent TO strategy to optimize the layout of damping material and the beam size of the lattice core; however, they did not consider the microstructure design problems of the damping layer. Zhang [26] proposed a concurrent TO method to design the free-layer damping structures with a maximum structural modal loss factor. In addition to the damping performance, the vibration response of the structures controlled by dynamic stiffness is equally important. To the authors’ knowledge, so far, limited researches have focused on the multi-scale topology optimization of composite plate structures in a frequency range. In this case, dynamic compliance is often used as the design objective for vibration response design [27][28][29][30][31][32][33]. In these studies, dynamic compliance is calculated using proportional damping, which cannot accurately consider the variation of damping due to the change of damping material configurations.
The rest of this paper is outlined as follows: Section 2 describes the general numerical computation method of dynamic compliance of the damping composite structures using the finite element method. Section 3 presents the mathematical optimization model of the proposed concurrent topology optimization method and elaborates the sensitivity analysis on the two scales. In Section 4, several numerical examples are presented to demonstrate the effectiveness of the proposed method. Finally, the design rules and conclusions are drawn in Section 5.
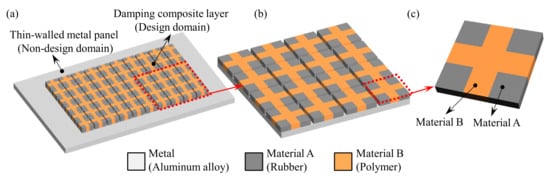
Materials 15 00538 g001 550
Figure 1. Two-scale composite plate design. (a) A composite plate consists of a metal panel and periodic damping composite. (b) Periodic damping composite. (c) Microstructure of the periodic damping composite.
 

This entry is adapted from the peer-reviewed paper 10.3390/ma15020538

References

  1. Li, B.; Huang, C.; Xuan, C.; Liu, X. Dynamic stiffness design of plate/shell structures using explicit topology optimization. Thin-Walled Struct. 2019, 140, 542–564.
  2. Nakra, B. Vibration Control in Machines and Structures Using Viscoelastic Damping. J. Sound Vib. 1998, 211, 449–466.
  3. Qatu, M.S.; Sullivan, R.W.; Wang, W. Recent research advances on the dynamic analysis of composite shells: 2000–2009. Compos. Struct. 2010, 93, 14–31.
  4. Rao, M.D. Recent applications of viscoelastic damping for noise control in automobiles and commercial airplanes. J. Sound Vib. 2003, 262, 457–474.
  5. Zhou, X.; Yu, D.; Shao, X.; Zhang, S.; Wang, S. Research and applications of viscoelastic vibration damping materials: A review. Compos. Struct. 2016, 136, 460–480.
  6. Danti, M.; Vigè, D.; Nierop, G.V. Modal Methodology for the Simulation and Optimization of the Free-Layer Damping Treatment of a Car Body. J. Vib. Acoust. 2010, 132, 021001.
  7. Alvelid, M.; Enelund, M. Modelling of constrained thin rubber layer with emphasis on damping. J. Sound Vib. 2007, 300, 662–675.
  8. Balmès, E.; Corus, M.; Baumhauer, S.; Jean, P.; Lombard, J.-P. Constrained viscoelastic damping, test/analysis correlation on an aircraft engine. Conf. Proc. Soc. Exp. Mech. Ser. 2011, 3, 1177–1185.
  9. Alvelid, M. Optimal position and shape of applied damping material. J. Sound Vib. 2008, 310, 947–965.
  10. Zheng, H.; Cai, C.; Pau, G.; Liu, G. Minimizing vibration response of cylindrical shells through layout optimization of passive constrained layer damping treatments. J. Sound Vib. 2005, 279, 739–756.
  11. Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224.
  12. Bendsøe, M.P.; Sigmund, O. Material interpolation schemes in topology optimization. Ingenieur-Archiv 1999, 69, 635–654.
  13. Alfouneh, M.; Tong, L. Maximizing modal damping in layered structures via multi-objective topology optimization. Eng. Struct. 2017, 132, 637–647.
  14. Kim, S.Y.; Mechefske, C.K.; Kim, I.Y. Optimal damping layout in a shell structure using topology optimization. J. Sound Vib. 2013, 332, 2873–2883.
  15. Yamamoto, T.; Yamada, T.; Izui, K.; Nishiwaki, S. Topology optimization of free-layer damping material on a thin panel for maximizing modal loss factors expressed by only real eigenvalues. J. Sound Vib. 2015, 358, 84–96.
  16. Ding, H.; Xu, B. Optimal design of vibrating composite plate considering discrete–continuous parameterization model and resonant peak constraint. Int. J. Mech. Mater. Des. 2021, 17, 679–705.
  17. Chen, W.; Liu, S. Microstructural topology optimization of viscoelastic materials for maximum modal loss factor of macrostructures. Struct. Multidiscip. Optim. 2016, 53, 1–14.
  18. Huang, X.; Zhou, S.; Sun, G.; Li, G.; Xie, Y.M. Topology optimization for microstructures of viscoelastic composite materials. Comput. Methods Appl. Mech. Eng. 2015, 283, 503–516.
  19. Zhang, H.; Ding, X.; Wang, Q.; Ni, W.; Li, H. Topology optimization of composite material with high broadband damping. Comput. Struct. 2020, 239, 106331.
  20. Ding, H.; Xu, B. Material microstructure topology optimization of piezoelectric composite beam under initial disturbance for vibration suppression. J. Vib. Control. 2021, 2021.
  21. Andreassen, E.; Andreasen, C.S. How to determine composite material properties using numerical homogenization. Comput. Mater. Sci. 2014, 83, 488–495.
  22. Liang, X.; Du, J. Concurrent multi-scale and multi-material topological optimization of vibro-acoustic structures. Comput. Methods Appl. Mech. Eng. 2019, 349, 117–148.
  23. Fang, Z.; Yao, L.; Tian, S.; Hou, J. Microstructural Topology Optimization of Constrained Layer Damping on Plates for Maximum Modal Loss Factor of Macrostructures. Shock. Vib. 2020, 2020, 1–13.
  24. Banh, T.T.; Luu, N.G.; Lee, D. A non-homogeneous multi-material topology optimization approach for functionally graded structures with cracks. Compos. Struct. 2021, 273, 114230.
  25. Zhu, J.-H.; Liu, T.; Zhang, W.-H.; Wang, Y.-L.; Wang, J.-T. Concurrent optimization of sandwich structures lattice core and viscoelastic layers for suppressing resonance response. Struct. Multidiscip. Optim. 2021, 64, 1801–1824.
  26. Zhang, H.; Ding, X.; Li, H.; Xiong, M. Multi-scale structural topology optimization of free-layer damping structures with damping composite materials. Compos. Struct. 2019, 212, 609–624.
  27. Olhoff, N.; Du, J. Generalized incremental frequency method for topological designof continuum structures for minimum dynamic compliance subject to forced vibration at a prescribed low or high value of the excitation frequency. Struct. Multidiscip. Optim. 2016, 54, 1113–1141.
  28. Takezawa, A.; Daifuku, M.; Nakano, Y.; Nakagawa, K.; Yamamoto, T.; Kitamura, M. Topology optimization of damping material for reducing resonance response based on complex dynamic compliance. J. Sound Vib. 2016, 365, 230–243.
  29. Xu, B.; Jiang, J.S.; Xie, Y.M. Concurrent design of composite macrostructure and multi-phase material microstructure for minimum dynamic compliance. Compos. Struct. 2015, 128, 221–233.
  30. Yang, X.; Li, Y. Topology optimization to minimize the dynamic compliance of a bi-material plate in a thermal environment. Struct. Multidiscip. Optim. 2012, 47, 399–408.
  31. Kang, Z.; Zhang, X.; Jiang, S.; Cheng, G. On topology optimization of damping layer in shell structures under harmonic excitations. Struct. Multidiscip. Optim. 2012, 46, 51–67.
  32. Olhoff, N.; Niu, B. Minimizing the vibrational response of a lightweight building by topology and volume optimization of a base plate for excitatory machinery. Struct. Multidiscip. Optim. 2016, 53, 567–588.
  33. Zhang, X.; Kang, Z. Dynamic topology optimization of piezoelectric structures with active control for reducing transient response. Comput. Methods Appl. Mech. Eng. 2014, 281, 200–219.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
ScholarVision Creations
Feedback