Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Engineering, Electrical & Electronic
A fitting solution to the sustainable-development conundrum is the microgrid. It can also be seen as a concept that is partly responsible for the changes in the topology of the power system. A microgrid is consisted of renewable energy sources such as solar PV panels, a micro-hydro power plant, a fuel cell with a hydrogen storage tank and a Li-ion storage unit.
- political optimizer
- LCOE
- economic dispatch
1. Introduction
The current topology of the power system is being modified by a host of factors including increasing energy consumption, penetration of renewable energy sources, decentralization and significant control-system implementation in order to satisfy the community-determined objectives such as cost or emissions minimization [1]. These changes are driven by a shift in the energy policies of both national and international governing bodies, as well as by the attitude of the people themselves, and are evidenced by the numerous binding agreements that have been signed, such as the Paris agreement [2] and the European green deal [3]. Both of these agreements promote sustainable development.
The definition of a microgrid is varied and depends upon the organization defining it. Nevertheless, the common attributes between the definitions provided by the US Department of Energy [4] and CIGRE [5] are that microgrids represent a group of interconnected loads and generating sources, they have well-defined electrical boundaries, they are controllable, they are decentralized power systems, they are equipped with robust communication and smart-grid technologies, and they can work in tandem with the grid or in a standalone mode. Finally, they are seen as a single entity by the Distribution System Operator (DSO).
An integral part of the modern microgrid is the Energy-Management System (EMS) which according to the International Electrotechnical Commission (IEC) standard 61970 is defined as a computer system consisting of various applications and support services that enable the effective operation of the power system so that the adequate security of the energy supply is maintained and is provided at a minimum cost. In general, from review articles found in the literature [6][7][8], the EMS of a microgrid has a host of functions which are shown in Figure 1. They include data acquisition, which involves the collection of data from various elements present in the microgrid such as generators, loads, storage devices, the main grid and weather forecasts. The acquired data is then appropriately processed according to the needs of the central computer of the microgrid, which could involve operations such as sampling, normalization, etc. Then comes forecasting, which involves predicting the time-dependent variables present in the microgrid such as the outputs of the weather-dependent renewable energy sources and the load demand. Forecasting in the long term (day ahead, week ahead and year ahead) is a process that is not performed online, and the forecasting referred to in Figure 1 is in the very short term (15 min ahead). This is because the short-term forecasts are more accurate than the long-term forecasts, and the plan for dispatch created 15 min before is much more accurate than the one created over a longer term. This process is succeeded by optimization which involves the creation of a schedule that balances power supply and demand over a period of time, which results in the Economic Dispatch (ED). This step is also the focus of this article. The final step involves the real-time control of the operation of the microgrid.

Figure 1. Functions of the EMS of the microgrid.
A hierarchical multi-agent approach using Particle Swarm Optimization (PSO) [9] for the energy management of a microgrid consisting of storage devices, renewable energy sources and electrical vehicles is presented in [10]. The objective function used in the study was the minimization of the operational cost and the innovativeness of the study comes from the low-computational-burden models that were created in order to simulate both the electrical and thermal characteristics of the system under consideration. The performance of the approach was evaluated over 3 different scenarios which considered the normal operation of the microgrid, the normal operation with autonomous capability and the analysis of the prosumer operations of the consumers under normal operating conditions. Overall, the implementation of the EMS was shown to reduce the costs by 11% in comparison with a business-as-usual approach. A multi-objective optimization approach considering cost minimization, PV-system-utilization rate and power fluctuations in a microgrid is presented in [11]. The study investigated the influence of demand-side response and Electrical Vehicle (EV) charging and discharging on the functioning of the microgrid under four different scenarios. The scenarios involved cases where both the controlled and uncontrolled charging of EVs were each considered with and without transferrable loads. For the purposes of optimization, a multi-objective seeker optimization algorithm was considered [12]. The microgrid model used consisted of elements such as PV panels, storage systems, EV charging ports, diesel engines and residential loads. The results showed an improvement in cost minimization, efficiency and security in the operation of the microgrid when controlled charging and demand-side response were considered together in comparison with the other explored scenarios. A mixed-integer, non-linear-programming approach to the optimization of an islanded water-energy-based microgrid is presented in [13]. The main purpose of the optimization model was to manage the demand for water within the water-distribution network, along with the smart management of electrical chillers for temperature moderation and, additionally, the management of electrical power generators. The study made an attempt to solve the ED problem on a day-ahead time horizon. The microgrid under consideration had numerous elements such as PV panels, energy-storage systems, conventional sources of power, both commercial and residential loads, and a comprehensive water-distribution network. In order to verify the performance of the proposed approach, a comparison was made between the cases wherein the ED was made with and without water-demand management and/or thermal management. The results indicated that hourly savings up to $150 can be made by including the water-distribution network within the ED problem, and that thermal management can additionally lower the hourly costs.
2. Investigated Optimization Algorithms
2.1. Political Optimizer
The PO is a socio-inspired, human-behavior-based, meta-heuristic optimization algorithm. It is based on the workings of political institutions and the electoral procedure. It is modeled on the steps that are usually followed in setting up a government, such as elections, the affairs of the parliament, the elections for constituencies, members defecting from one party to another, and in general the campaigns held by all of the stakeholders in the elections [14]. The effectiveness of this algorithm in locating the final global minimum solution comes from its dual-sided approach. The first approach involves every individual that represents a solution candidate trying to win an election, and the second approach involves every contesting political party trying to form a government by gaining a majority of the seats in the parliament.
The solution-searching process of the algorithm is as follows: it begins with a declaration of the population size that is then divided into n political parties that consist of n members. Every member of every party represents a candidate solution and is a vector of the decision variables of the problem. During this step the algorithm calculates the number of constituencies, which aids in locating the best party member at a particular index within a party, and is equal to the number of parties and members n. This concept is illustrated in Figure 2.

Figure 2. Constituency allocation.
2.2. Lichtenberg Algorithm
The Lichtenberg Algorithm (LA) is a nature-inspired, meta-heuristic approach based on the exploitation of fractal power. It takes advantage of the randomness involved in the Lichtenberg-Figure (LF) formation and incorporates it into the solution-searching process. A well-known example of an LF is lightning formation in clouds.
In fact, lightning formation is the real-world phenomenon upon which the LA is based. Lightning is formed as a result of an electrical discharge from electrical fields that are formed due to the relative movement of clouds amongst one another and the resulting friction. They can be categorized into many different types, such as ground-to-cloud, inter-cloud and intra-cloud, cloud-to-ground and cloud-to-atmosphere. Amongst all the types of lightning propagation, the intra-cloud phenomenon is the most apt for an optimization algorithm due to its area coverage, which is considerably higher than in the case of the other lightning types. This propagation creates an LF that can be recreated in a laboratory by witnessing an electric discharge on di-electric materials [15].
A well-known approach for creating LFs is the Diffusion Limited Aggregation (DLA) which creates them via cluster formation [16]. Two inputs are needed for this approach, which are the cluster size and number of particles. Once these two parameters are defined, a random figure is generated by utilizing fractal geometry. Two such figures that were created on different runs of the algorithm are shown in Figure 3, and it can be seen that they are quite different despite being created from the same parameters. This randomness in formation aids in the exploration of the solution-search space for the optimization algorithm.

Figure 3. Lichtenberg figure.
3. Microgrid Layout, Mathematical Model and LCOE Calculations
3.1. Microgrid Layout
The layout of the microgrid is presented in the Figure 4 and was partially modeled on the setup at Wroclaw University of Technology. In total, the number of generators is 10 (including storage) and the number of loads is 13 (including storage). Amongst the generators were four PV panels with peak powers of 13 kW, 12.5 kW, 8 kW and 16.5 kW, two diesel generators with a rating of 4.8 kW/6 kVA, a Li-ion battery system (BESS) with a capacity of 9.8 kWh, a fuel cell (FC), a hydrogen storage tank (HST) with a capacity of 4.2 kWh, and finally a micro-hydro power plant with a peak power of 10.46 kW. The loads were modeled according to the values provided in Figure 4.

Figure 4. Microgrid layout.
The nodes of the microgrid were interconnected by aluminum cables that were XLPE insulated and had an outer sheath composed of PVC. The electrical characteristics of the cable are summarized in Table 1.
Table 1. Cable data.
| From | To | Distance (m) | r + jx (Ω) (10−1) |
|---|---|---|---|
| node 1 | node 2 | 180 | 0.455 + 0.147j |
| node 2 | node 3 | 130 | 0.329 + 0.106j |
| node 3 | node 4 | 145 | 0.367 + 0.118j |
| node 4 | node 5 | 195 | 0.493 + 0.159j |
| node 5 | node 1 | 140 | 0.354 + 0.114j |
| node 2 | node 5 | 190 | 0.481 + 0.155j |
3.2. LCOE Calculations
Any microgrid is inherently diverse with regard to the multiple sources of renewable energy that are present within its energy mix. In order to compare the cost-effectiveness of all the different generators available and aid in investment planning, the LCOE is used [17][18]. The calculations result in the assertion of price per unit of energy produced for every generator type in the microgrid, and take into account the total investment costs such as the capital cost and the cost of installation. Additionally, it considers the operational and maintenance costs and any other costs one may encounter during the lifetime of the generator. The total energy produced by a generator type over its lifetime is also assumed. It is important to mention here that the LCOE is a static metric and not a dynamic one since it remains unchanged during the project lifetime. It is also a metric that is spatially dependent since the lifetime performance of renewable-energy-based generators is very much region specific.
4. The Operation of the Microgrid from A Yearly Standpoint
In order to understand the operation of the microgrid from a yearly standpoint, clustering was employed in order to split the yearly load data. In this case, the optimal number of clusters was determined using the elbow method and the clustering algorithm used was k-means clustering [19][20]. Both of these methods are quite popular and can be found in numerous references such as in [21].
Figure 5 provides figures with respect to the clustering of the yearly load data and the yearly power output of the microgrid. The Within Cluster Sum of Squares (WCSS) process was used in order to determine the optimal number of clusters, which was three. From each cluster, a representative day was chosen. In general, they can be correlated with the seasonal changes in Poland. Cluster 1 in Figure 5a has a load demand between those of clusters 2 and 3, which represent the spring/autumn months. Cluster 2 in Figure 5a had the highest load demand and is typical of winter, whereas cluster 3 in Figure 5a had the lowest load demand and is typical of the summer months.
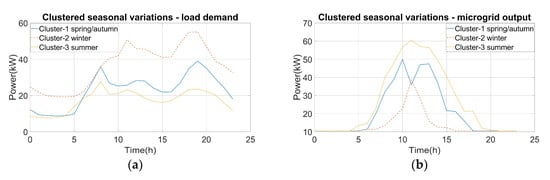
Figure 5. Clustered seasonal load variations (a) and clustered seasonal variations in microgrid output (b).
There are also generation data that corresponding to the load data of the days that represent the different clusters. This information is provided in Figure 5b, wherein cluster 1 is typical of the microgrid generation during the spring. Cluster 2 is characteristic of the winter, during which the microgrid energy generated was low throughout the day, and cluster 3 is characteristic of the summer when the microgrid energy production is at its maximum.
The microgrid storage devices operations are presented in Figure 6a,b. In Figure 6a for cluster 1, it can be seen that the Li-ion storage device was charged around mid-day. This is when the microgrid power generation exceeded the load demand, and it began discharging in the evening when the load demand exceeded the power that was generated in the microgrid. A similar characteristic is seen with the hydrogen storage device in Figure 6b for cluster 1. The microgrid operation for cluster 2 shows that the Li-ion storage device was charged to full capacity at mid-day, but it discharged immediately. In fact, on certain winter days the Li-ion storage device did not charge at all. This was because on most winter days, the load demand was greater than the microgrid power generation for much of the day. The hydrogen storage tank for cluster 2 was filled only up to 27% of its capacity due to the lack of excess net energy in the microgrid. The microgrid operation for cluster 3 shows that the Li-ion storage device was charged to full capacity in the morning and did not discharge until the evening. This was because of the high microgrid power generation during the day compared to the load demand. The hydrogen storage device also reached its maximum capacity due to an excess of net energy in the microgrid.

Figure 6. Charging/discharging: battery storage system (a) and hydrogen storage system (b).
Figure 7a represents the dynamic microgrid interaction with the main grid. It can be deduced that for cluster 1 during mid-day, when the power generated within the microgrid was higher than the load demand, the power was exported to the main grid, whereas during the evening when the load demand was higher than the energy produced, it was imported. Figure 7b provides the price signal as a result of LCOE minimization by the optimizer, and it can be seen that the price signal remained below 0.1 USD/kWh for most parts of the day except when the fuel cell discharged. This is because the LCOE of the hydrogen-based generator is much higher when compared to the others. For cluster 2, it can be seen that, unlike in the case of cluster 1, where power was exported to the main grid during mid-day, there was only the importation of power from the main grid due to the high load demand and the low energy supply in the microgrid. The price signal for cluster 2 stayed below 0.1 (USD/kWh) with the exception of two small spikes. In comparison to cluster 1, the spike is lower in magnitude because in the earlier case the hydrogen storage reached full capacity and the fuel cell ran longer, and in this cluster the fuel cell ran for a shorter time. For cluster 3, it can be inferred that for much of the day the power was being exported to the main grid due to the high generation in the microgrid. This fact is also reflected in the price signal, where it can be seen that the price stayed close 0.02 USD/kWh, which is the lowest for all three seasonal clusters, and that there are two spikes in this case, which strictly point to the fuel-cell operation due to its high LCOE.

Figure 7. Microgrid interaction with the main grid (a) price signal (b).
This entry is adapted from the peer-reviewed paper 10.3390/electronics10243119
References
- Mosa, M.A.; Ali, A.A. Energy management system of low voltage dc microgrid using mixed-integer nonlinear programing and a global optimization technique. Electr. Power Syst. Res. 2021, 192, 106971.
- Paris Agreement. United Nations Paris Agreement. 2015. Available online: https://unfccc.int/sites/default/files/english_paris_agreement.pdf (accessed on 8 September 2021).
- European Comission. The European Green Deal; European Comission: Brussels, Belgium, 2019.
- Ton, D.T.; Smith, M.A. The U.S. Department of Energy’s Microgrid Initiative. Electr. J. 2012, 25, 84–94.
- Marnay, C.; Chatzivasileiadis, S.; Abbey, C.; Iravani, R.; Joos, G.; Lombardi, P.; Mancarella, P.; Von Appen, J. Microgrid evolution roadmap. In Proceedings of the 2015 International Symposium on Smart Electric Distribution Systems and Technologies (EDST), Vienna, Austria, 7–11 September 2015; pp. 139–144.
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055.
- Suresh, V.; Janik, P.; Guerrero, J.M.; Leonowicz, Z.; Sikorski, T. Microgrid Energy Management System with Embedded Deep Learning Forecaster and Combined Optimizer. IEEE Access 2020, 8, 202225–202239.
- Vera, Y.E.G.; Dufo-López, R.; Bernal-Agustín, J.L. Energy management in microgrids with renewable energy sources: A literature review. Appl. Sci. 2019, 9, 3854.
- Kaczorowska, D.; Rezmer, J.; Sikorski, T.; Janik, P. Application of PSO algorithms for VPP operation optimization. Renew. Energy Power Qual. J. 2019, 17, 91–96.
- Farinis, G.Κ.; Kanellos, F.D. Integrated energy management system for Microgrids of building prosumers. Electr. Power Syst. Res. 2021, 198, 107357.
- Hou, H.; Xue, M.; Xu, Y.; Xiao, Z.; Deng, X.; Xu, T.; Liu, P.; Cui, R. Multi-objective economic dispatch of a microgrid considering electric vehicle and transferable load. Appl. Energy 2020, 262, 114489.
- Shafik, M.B.; Chen, H.; Rashed, G.I.; El-Sehiemy, R.A. Adaptive multi objective parallel seeker optimization algorithm for incorporating TCSC devices into optimal power flow framework. IEEE Access 2019, 7, 36934–36947.
- Moazeni, F.; Khazaei, J. Dynamic economic dispatch of islanded water-energy microgrids with smart building thermal energy management system. Appl. Energy 2020, 276, 115422.
- Askari, Q.; Younas, I.; Saeed, M. Political Optimizer: A novel socio-inspired meta-heuristic for global. Knowl.-Based Syst. 2020, 195, 105709.
- Niemeyer, L.; Pietronero, L.; Wiesmann, H.J. Fractal Dimension of Dielectric Breakdown. Phys. Rev. Lett. 1984, 52, 1033–1036.
- Witten, T.A.; Sander, L.M. Diffusion-limited aggregation. Phys. Rev. B. 1983, 27, 5686.
- Branker, K.; Pathak, M.J.M.; Pearce, J.M. A review of solar photovoltaic levelized cost of electricity. Renew. Sustain. Energy Rev. 2011, 15, 4470–4482.
- Jones-albertus, R.; Feldman, D.; Fu, R.; Horowitz, K.; Woodhouse, M. Technology advances needed for photovoltaics to achieve widespread grid price parity. Prog. Photovolt. Res. Appl. 2016, 24, 1272–1283.
- Jasiński, M.; Sikorski, T.; Borkowski, K. Clustering as a tool to support the assessment of power quality in electrical power networks with distributed generation in the mining industry. Electr. Power Syst. Res. 2019, 166, 52–60.
- Jasiński, M.; Sikorski, T.; Kostyła, P.; Leonowicz, Z.; Borkowski, K. Combined Cluster Analysis and Global Power Quality Indices for the Qualitative Assessment of the Time-Varying Condition of Power Quality in an Electrical Power Network with Distributed Generation. Energies 2020, 13, 2050.
- Andrew, N. Machine Learning Yearning, Technical Strategy for AI Engineers in the Era of Deep Learning. 2018. Available online: https://storage.googleapis.com/kaggle-forum-message-attachments/693524/14574/ML_book.pdf (accessed on 8 September 2021).
This entry is offline, you can click here to edit this entry!
