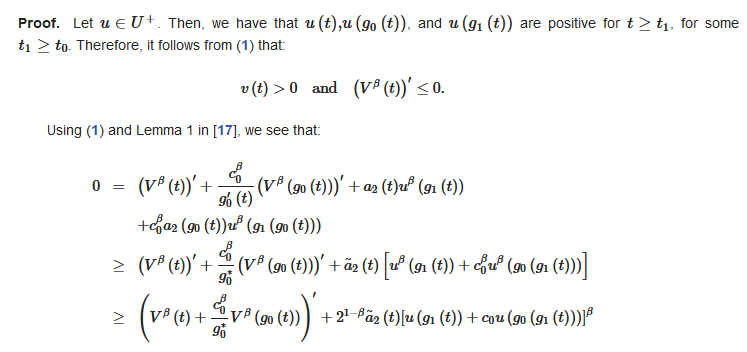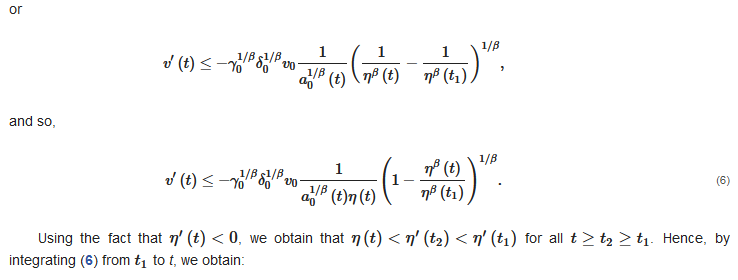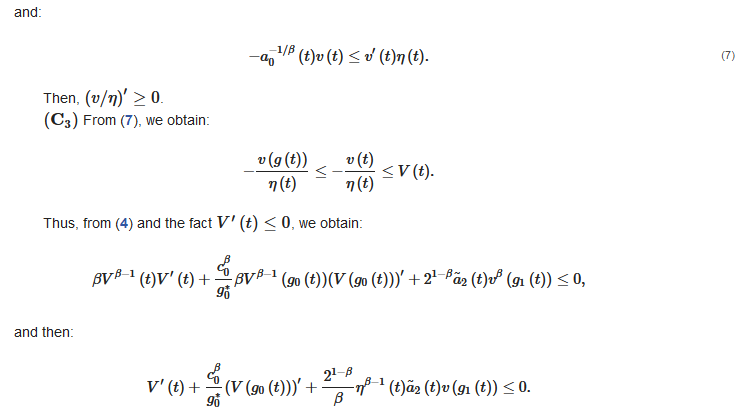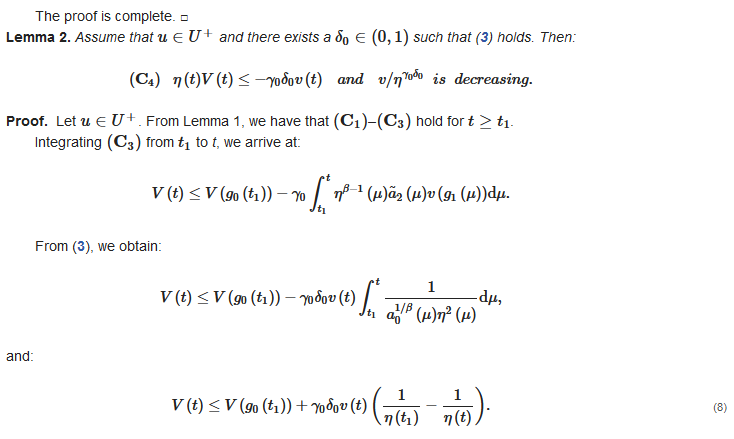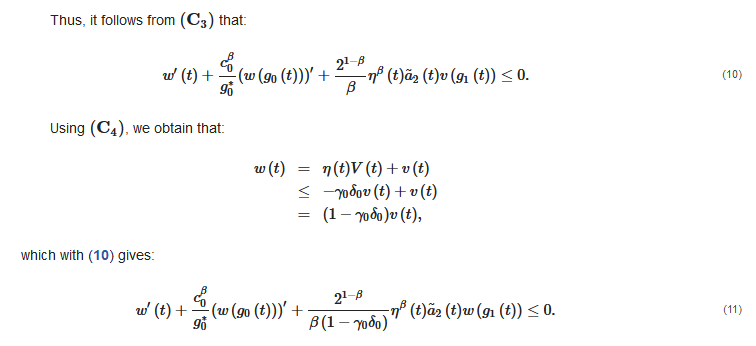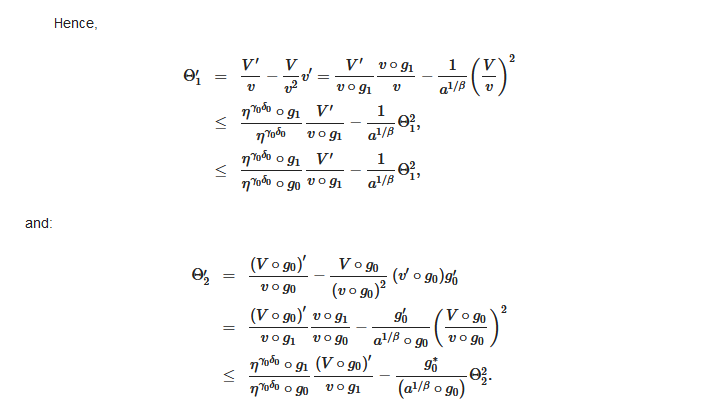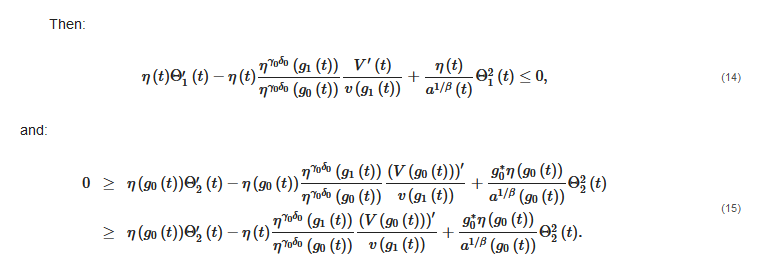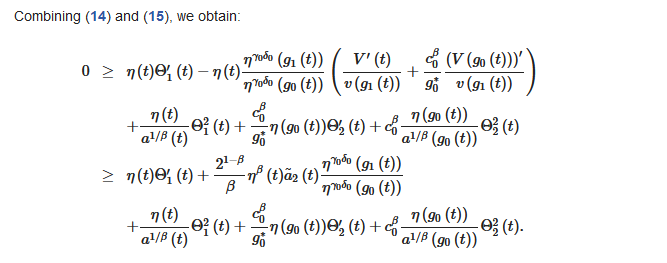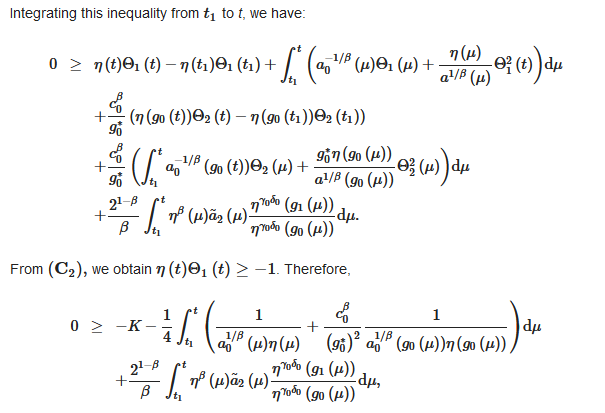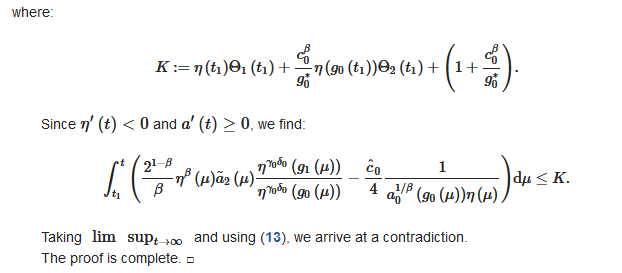A DDE is a single-variable differential equation, usually called time, in which the derivative of the solution at a certain time is given in terms of the values of the solution at earlier times. Moreover, if the highest-order derivative of the solution appears both with and without delay, then the DDE is called of the neutral type. The neutral DDEs have many interesting applications in various branches of applied science, as these equations appear in the modeling of many technological phenomena. The problem of studying the oscillatory and nonoscillatory properties of DDEs has been a very active area of research in the past few decades.
- delay differential equation
- neutral
- oscillation
- noncanonical case
1. Introduction
Consider the 2nd-order delay differential equation (DDE) of the neutral type:

The oscillatory properties of solutions of second-order neutral DDE (1) in the noncanonical case, that is:
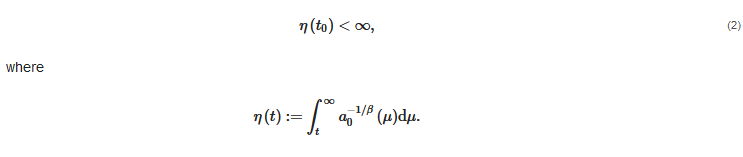
2. Oscillatory Properties of Noncanonical Neutral DDEs of Second-Order

2.1. Auxiliary Lemmas

2.2. Oscillation Theorems
in the next theorem, by using the principle of comparison with an equation of the first-order, we obtain a new criterion for the oscillation of (1).

2.3. Applications


This entry is adapted from the peer-reviewed paper 10.3390/math9172026