A solution is to develop a suitable estimation strategy which led scholars to propose different temperature estimation schemes aiming to establish a balance among accuracy, adaptability, modelling complexity and computational cost. This article presented an exhaustive review of these estimation strategies covering recent developments, current issues, major challenges, and future research recommendations. The prime intention is to provide a detailed guideline to researchers and industries towards developing a highly accurate, intelligent, adaptive, easy-to-implement and computationally efficient online temperature estimation strategy applicable to health-conscious fast charging and smart onboard BMS. Full Paper:https://doi.org/10.3390/en14185960
- electric vehicles
- machine learning
- Kalman filter
- thermal modelling
- online prediction
- electromagnetic impedance spectroscopy
- computational cost
1. Introduction
Lithium-ion batteries (LIBs) are widely used in electric vehicles (EVs), grid-tied stationary energy storage systems, and several other consumer electronics primarily due to their high voltage rating (>4 V/cell) and high energy density (~265 (W h) L −1 ) and longer operational life. The use of LIBs in automotive and aerospace applications has led to larger cell sizes and large battery packs for a higher driving range and the requirement for more aggressive charging and discharging. However, thermal instability and temperature-dependent nonlinear behavior is some of the common concerns behind the safe and reliable operation of LIB systems. It is noticed that the operation of batteries outside the safe operating temperature directly affects the performance of LIBs, such as cycle life, efficiency, reliability and safety. Researchers investigating the thermal performance of LIB showed that the best operating temperature range is from 25 °C to 40 °C [1,2]. Richardson et al. [3] demonstrated that the difference between the core and surface temperature could reach more than 10 °C during real-life applications, especially during the high discharging condition and fluctuating load current demand. The excessive temperature difference and the accumulation of a large amount of heat inside the cell could lead to thermal runaway or even explosions and fire [4]. That necessitates the employment of a battery management system (BMS) for effective monitoring of battery parameters (current, voltage, temperature), estimation of battery states (state of charge (SOC), state of health (SOH), remaining useful life (RUL), state of temperature (SOT) [5]). Research studies demonstrated that SOC [6], SOH [7], and remaining storage capacity [8] are a function of temperature; thus, the estimation of the battery states also depends on the accurate estimation of cell temperature. The Columbic efficiency of a cell is greatly affected by the cell temperature during the charging and discharging period. Few other popular functionalities of BMS include cell balancing [9] and fault detection/diagnosis [10] to ensure optimum capacity utilization, operational safety, reliability, and longer battery life often requires temperature information of an individual cell and battery pack as well. Therefore, accurate information of core and surface temperature is highly crucial for effective thermal management and safety of a LIB pack. Moreover, in cold climate areas, the battery capacity is drastically reduced due to low-temperature operation that requires preheating the battery to a suitable range for optimum performance [11,12]. It is also evidenced that for every 0.1 °C beyond the safe operating region the battery capacity degrades by about 5% [13]. It is evidenced that maximum heat is generated during the discharging period especially with fast discharging [14]. Therefore, accurate temperature estimation is essential for effective thermal management and safety during fast charging and discharging and preheating of the cell to minimize capacity fade.
In summary, it could be stated that the accurate information of cell temperature is undoubtedly serving as the essential basis for the thermal management and safety of LIB. While the surface temperature of each cell can be measured by installing a temperature sensor on each cell, the core or internal temperature measurement directly using physical sensors is challenging. Moreover, installing a temperature sensor on each cell surface is not practically feasible from a system cost, space and weight point of view as any high-capacity battery pack used in EVs and grid-tied systems essentially consists of thousands of individual cells. Researchers have also incorporated multi-dimensional sensing and self-healing functions into a single battery cell to develop a smart battery [15,16,17,18]. Smart cells are typically capable of parameter measurements and estimation of cell states including the state of temperature. Despite the modularized application of BMS in smart batteries, accurate temperature estimation is still required, as otherwise installing sensors in each cell results in high implementation cost and complexity. Therefore, researchers are struggling hard to develop a high-fidelity, accurate, easy-to-implement, and computationally inexpensive online temperature estimation strategy suitable for low-cost onboard BMS. Several temperature estimation techniques have been proposed by researchers so far. Each different type of method has its advantages and limitations with respect to the above-mentioned features of an optimum BMS. Therefore, a summary of all the prominent techniques would be very helpful to researchers and developers serving as a baseline for further research and as a guideline for selecting appropriate techniques suitable for a specific requirement. However, such a summary with detailed discussion on current progress and explanation of the existing issues, challenges and future research scopes has not yet been presented in the literature. Therefore, this article covered the research gap by conducting a comprehensive review of the state-of-the-art temperature estimation strategies reported in the literature so far.
2. Generic Temperature Estimation Strategy
Irrespective of battery chemistry, heat is accumulated inside the battery during the charging/discharging even during idle conditions, majorly due to several largely exothermic chemical and electrochemical reactions as well as transport processes. If the heat transfer from the battery to the surroundings is not sufficient, then the heat gets accumulated inside the battery resulting in an increase in core and surface temperature, thereby risking thermal runaway. This phenomenon is even more prominent in the case of hard-cased insulated batteries (as used in EVs), under fast charging/discharging and the operation in hot environments. Heat dissipation is worse in cylindrical LIBs that are extensively used in high-capacity LIB packs. Therefore, a typical temperature estimation scheme consists of two models, namely, a heat generation model and a heat transfer model [19]. Often, a battery electrical model is also used to estimate the total heat generation using Bernardi’s [20] heat generation model whereas few other models use a mathematical form of battery electrochemistry to calculate the heat generation. Adaptive estimation strategies also consider the influence of different battery states, such as SOC and SOH, as the battery temperature is a function of these battery states. Then, the heat transfer model takes the estimated total heat quantity as well as few other external measurements such as ambient temperature to predict the temperature of that cell. Closed-loop estimation schemes use the measured or the estimation temperature as feedback to improve the prediction accuracy. A schematic layout of a generic temperature estimation strategy for LIB is shown in Figure 1 .
3. Classification of Temperature Estimation Strategies
As shown in Figure 1 , typically, a temperature estimation scheme consists of a heat generation model and a heat transfer model. The heat generation models reported in the literature can be broadly classified from two different aspects; based on modelling strategy and based on the source of heat generation. Heat generation models based on modelling strategy can be classified into three groups, physics-based electrochemical models [21,22,23,24], equivalent circuit models (ECM) [25,26,27], black-box models [28,29,30]. In contrast, based on the source of heat generation, these models can be grouped as a concentrated model, distributed model [31] and heterogeneous model [25,32]. The concentrated heat generation model considers that all heat is generated at the core only, usually considered to reduce the modelling complexity. The distributed heat generation model considers that uniform heat is generated throughout the entire cell geometry whereas the heterogeneous model can capture different heat generation from difference cell layers usually resulting in temperature and current density gradients inside the cell. The heterogeneous models are more detailed thus can produce highly accurate predictions; however, these are most complex and require extensive experiments for modelling. Distributed heat generation models are a balance between the concentrated and heterogeneous models. The heat transfer models can be classified into finite element analysis (FEA)-based models [27,33,34,35,36], heat capacitor-resistor models (lumped or distributed parameter) [28,37,38,39,40], and data-driven techniques. Heat capacitor–resistor-based models use the analogy between electrical and thermal systems. A heat capacitor–resistor can be further classified as mentioned in Figure 2 . Lumped parameter models are simple and useful for online applications, however, only one or two average temperatures can be predicted with these models whilst the battery temperature distribution is not spatially uniform, especially in larger capacity cylindrical LIB cells. On the other hand, complex distributed models [41,42] can describe the detailed temperature distribution in a cell, however, they are not suitable for online application due to their computational complexity. Several other detailed models of LIB accounting for the thermal characteristics of different layers are studied in [43,44,45,46,47,48]. A two-state/node model provides information on core and surface temperature whereas a one-state/node model can provide only core temperature.
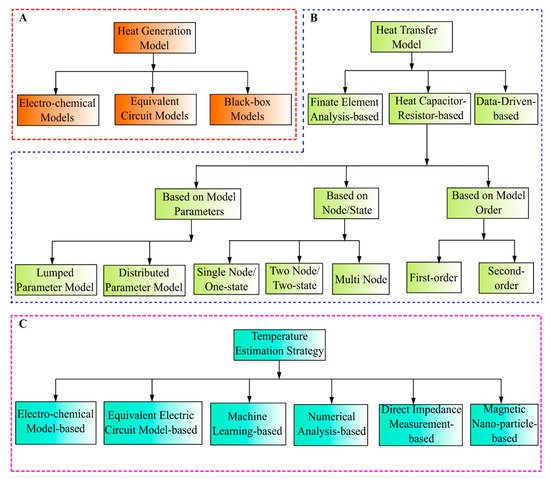
The heat transfer model where the total heat generation is one of the input parameters is collectively called the battery thermal model where the total heat generation is estimated by the battery heat generation model. The thermal modelling of LIB is a separate area of study and is not under the scope of this study. It deals only with the temperature estimation strategies. However, as most of the temperature estimation strategies are extensively depending on thermal modelling, an overview of each modelling technique is also discussed with the respective temperature estimation strategy for better understanding. Researchers employed different types of heat generation models with different kinds of heat transfer models to come up with a temperature estimation scheme. Therefore, it is challenging to classify these estimation strategies. Broadly, the temperature estimation schemes can be grouped into electrochemical thermal modelling-based, equivalent electric circuit model (EECM)-based, machine learning (ML)-based, numerical-model based, direct impedance measurement-based, magnetic nanoparticles-based schemes. The families of the LIB heat generation model, heat transfer model and temperature estimation strategy are illustrated in Figure 2 .
4. Comprehensive Review of Temperature Estimation Strategies
Further, depending on the modelling complexity, EECM could be also classified as lumped-parameter and distributed parameter models. Lumped-parameter models are used for simplification and thus low computational cost compared to detailed distributed models. Computationally efficient lumped thermal models are developed using single temperature as input to capture the model parameters [70] while some researchers used both surface and core temperatures of the cell to construct the lumped thermal models. Some also considered the correlation between cell geometry and other physical properties with thermal modelling [71]. However, several assumptions were made during modelling leading to inaccurate temperature estimation compared to detailed thermal modelling. Further, thermal models that only estimate the core temperature are considered as single-state/node [72], whereas if the model can estimate both surface and core temperature then it is termed as two-state/node [67] thermal model. The parameters of the EECM are identified through ranges of experimental studies such as electrochemical impedance spectroscopy (EIS) or utilizing externally measurable quantities, such as voltage, current, and temperature. Few studies also considered various conditions of SOC, SOH and estimated surface/core temperatures to make the model more robust. It is very difficult to group those thermal models because lumped models are used in both single-state and dual-state modelling and the model could be first-order and second-order. Therefore, the literature is grouped into cell-level and pack-level temperature estimation schemes that are discussed below.
Cell internal temperature estimation using a lumped-parameter thermal model and an approximate distributed thermal model have several drawbacks. Firstly, accurate determination of thermal model parameters such as heat generation and cell thermal properties is highly challenging. Heat generation inside the cell is typically approximated by measuring the cell operating current, voltage and the internal resistance that are again functions of SOC, cell internal temperature and SOH. Moreover, a cell is constructed using many different materials combined into a layered structure and thermal contact resistances between these layers are often unknown. Temperature estimation methods use surface temperature measurements and even the combination of surface-mounted temperature sensor and thermal model typically failed to detect the thermal runaway as rapid fluctuations in the internal temperature is difficult to capture using surface-mounted sensors because the heat conduction between the core and battery surface takes a considerable amount of time [92]. Furthermore, embedding micro-temperature sensors within the cell [93,94] is not practically possible for a large capacity LIB pack from a manufacturing complexity and system cost point of view. Hence, the core temperature measurement using a physical sensor is not an appropriate method for industrial applications.
Online EIS-based temperature estimation strategy termed impedance-temperature detection (ITD) was proposed by Richardson and Howey [100] for sensorless temperature estimation which is adaptive to cell ageing and practical uncertainties. However, ITD cannot provide a general solution alone, thus, such a strategy combines surface-mounted sensors with ITD for accurate online temperature estimation [3]. Still, temperature sensors are required to be installed. Further to this study, they integrated ITD with an electric-thermal model along with a DEKF for online core temperature estimation of a LIB cell even with unknown convection coefficient. They also demonstrated that the performance of the thermal model plus ITD is almost similar to the ITD with surface thermal sensors. Despite the advantages, the major limitations of the strategy are online impedance determination and the requirement of an accurate electric thermal model, thus encompassing the same drawback of conventional thermal modelling-based strategies. Moreover, although the strategy can estimate both core and surface temperature of an individual cell, the pack-level estimation strategy was not illustrated in this study.
The influence of cell temperature, SOC and SOH on the impedance spectrum, excitation frequency and thereby estimation accuracy of cell internal temperature was investigated by Zhu et al. [101]. Here, the temperature estimation was made based on an impedance response matrix analysis which was developed using EIS measurements. Despite high accuracy, the effect of the nonuniformity of the cell temperature and the correction method was not considered. Moreover, an extensive experimental study is required for modelling and the computational cost is also very high. Thus, the online application of the strategy is challenging. Identification of suitable frequency and other EIS parameters is very difficult whilst the estimation accuracy significantly depends on these parameters. Moreover, accurate determination of the real and imaginary parts of the impedance is highly challenging, whilst different decisions for these two parts lead to inaccurate temperature estimation. A combination of Linear Parameter Varying (LPV) thermal model and a polytopic observer-based battery-cell temperature estimation algorithm was proposed by Debert et al. [102]. The EIS-based strategy was also employed in references [3,103,104,105,106] to estimate the core temperature. Despite high accuracy, the major limitation is the determination of accurate impedance-temperature characteristics and it should be acquired in advance through tedious preliminary tests. In addition, the impedance-temperature characteristic of a cell is influenced by cell ageing leading to inaccurate prediction due to SOH deterioration. A summary of direct impedance measurement-based temperature estimation strategies is presented in Table 4 .
| Reference | Types of Models | Important Note |
|---|---|---|
| Srinivasan et al. [95,96] | Direct measurement of electrochemical impedance | Experimental validation with EIS data |
| Schmidt et al. [97] | Direct measurement of electrochemical impedance | Temperature non-uniformity was not considered, experimentally validated |
| Richardson et al. [3] | Thermal-impedance model + EIS measurement at single frequency + surface temperature feedback | Independent of cell thermal properties, heat generation or thermal boundary conditions, experimental validation with EIS data |
| Richardson and Howey [100] | Online EIS measurement (impedance-temperature detection (ITD) + dual-extended Kalman filter (DEKF) | Unknown convection coefficient is considered, experimentally validated |
| Zhu et al. [101] | Impedance response matrix analysis, developed using EIS measurements | Influence of cell temperature, SOC and SOH on the impedance spectrum, experimental validation with EIS data |
This entry is adapted from the peer-reviewed paper 10.3390/en14185960
