The battery modelling (BM) problem is a constrained, multi-dimensional, mixed variable, non-convex, non-linear optimisation problem. Many bio-inspired techniques have been successfully employed to estimate the battery parameters. When bio-inspired algorithms are implemented for COM to extract parameters in real time, then they are called grey box models.
- electrochemical models
- mathematical models
- circuit-oriented models
- black box modelling
- grey box modelling
1. Introduction
The lifetime of any battery depends on its physical properties. The aging of battery cells is also nonlinear. A battery’s lifetime cannot be extended by minimising the power consumption at a particular point. Rather, it depends on the way the power is consumed, as well as current extraction patterns and current levels. Moreover, continuous drawing of high current inhibits the residual capacity [1]. Battery Management system (BMS) are essential to ensure the safe, fail-safe and efficient operation of batteries.
The main function of battery management systems is ensuring the safe operation of a battery, controlling a battery’s charge and discharge process, cell balancing, over temperature protection and estimating the state-of-charge (SoC) by measuring voltage, current and temperature. BMS monitors the conditions and state of the battery such as SoC, state-of-health (SoH), Depth of Discharge (DoD) and operating temperature [2,3]. However, these states are to be inferred from the state estimators that depend on the battery model. Therefore, the modelling of a battery becomes an important role in studying, estimating or predicting the real-time operation of the battery.
The mathematical modelling of a battery is significant because of the following reasons: (i) Development of efficient BMS. (ii) Key in the improvement of charging/discharging techniques and the enhancement of battery capacity. (iii) Need to capture the influence of power consumption on the battery. (iv) To prevent serious damage to batteries from overcharging or over-discharging. (v) Faster and safer way to study battery behaviour under different operating conditions. (vi) Identifying the operating limits that achieve best lifetime for specific applications.
This paper examines numerous battery models for various types of batteries, including electrochemical models, mathematical models, circuit-oriented models and combination models. There is a lot of scope for researchers to investigate the deployment of Artificial Intelligence in a variety of disciplines as it emerges around the world and makes laborious tasks easier. As a result, the applications of numerous machine learning and meta-heuristic methods for battery management systems are discussed in this paper. Furthermore, using evolutionary algorithms, a study was conducted to extract parameters from a lithium-ion battery model.
2. Types of Battery Modelling
A wide variety of battery models have been developed with differing complexities which can be useful in various application areas [4,5,6,7,8,9,10]. According to the degree of physical insight, battery models can be differentiated into three levels, viz., white box model (e.g., electrochemical model), grey box model (e.g., circuit-oriented model) and black box model (e.g., artificial neural network (ANN) model) [11]. An important factor in the modelling of a battery is the estimation of battery parameters. Different modelling strategies for extracting the battery parameters are electrochemical, mathematical, circuit-oriented and data-driven [12,13].
In order to simplify calculations, the SP model was developed for the condition of low-rate charge and discharge. This model makes the assumption of even distribution and concentration of lithium ions in the liquid phase everywhere in the battery and also assumes that the electric potential of the solid phase is constant in the electrode. Compared with the P2D model, the SP model has fewer solving equations, fewer parameters and higher solving efficiency. However, this oversimplification reduced the accuracy of the model. In order to deal with these shortcomings, an extended SP model was developed, in which liquid phase diffusion and heterogenous reactions were considered. While the SP model simplifies the P2D model by virtually eliminating the partial differential equations that deal with liquid phase diffusion and also simultaneously reduces the electrode to a single particle of consideration, the extended SP model further simplifies the electrode into a single active particle but no longer directly solves the partial differential equation by iteration, but uses curve fitting or approximate solution to process the partial differential equation. Although the complexity of the model has increased by this process in the computation of an extended SP model, the actual computational efficiency has not decreased too much due to the avoidance of iterative solving [23].
Summarising, there is no doubt that good electrochemical battery models serve as some of the most accurate among battery models, due to the very fact that they can mathematically explain key behaviours of a battery at the microscopic scale based on the basis of chemical reactions occurring inside the battery in the liquid phase and in the electrode. Considering accuracy as the most important aspect of modelling, these models are excellent and can be used to complement experimental data for evaluation of other models. One advantage of electrochemical models over real data is that internal states are fully observable, allowing ‘virtual measurements’ of quantities that cannot be measured in practice. They are able to even record the changes caused by temperature changes. As these temperature changes result in different responses from an electrochemical perspective, these models can account for fluctuations and changes in temperature [26].
Based on the Shepherd discharge model, mathematical models are mainly developed to predict system-level behaviour. Empirical equations or math-based stochastic models are used in mathematical models, which only evaluate the charge recovery effect and ignores all other factors. The number of equations is reduced and simplified compared to the electrochemical model [29]. These models monitor the non-linear relationship between the real-time operation of the battery and the discharge rate without considering the recovery effect [7,30]. The use of mathematical models is very low, because the relation with the parameters of the model and I-V characteristics is not sufficient [16].
3. Battery Modelling Using Black Box Modelling Data-Driven Techniques
Many soft computing and optimisation techniques have been developed for battery parameter estimation. These techniques are called data-driven approaches which include (a) fuzzy-based estimation, (b) fuzzy-based neural network, (c) artificial neural network, (d) bio-inspired algorithm, (e) support vector machine, etc.
Since the default capabilities required for performing machine learning (ML) algorithms are generally included in BMS, ML techniques for modelling charging/discharging profiles are promising. Large amounts of data storage and robust data analytic tools are essential for ML model implementation. ML techniques are adaptable to any changes in the system and need minimum resources. Modelling is a fairly simple process that can be carried out based on the amount of information given. Modelling the charging/discharging profiles of battery systems can be performed using various machine learning tasks such as pattern recognition, clustering and classification. For predicting the charging and discharging behaviour of any battery system, models based on an artificial neural network and ML techniques other than ANN are also employed.
Machine learning outperforms traditional methods when it comes to predicting battery parameters due to its ability to deal with nonlinearity. By implementing a learning model, a general machine learning system for monitoring battery conditions can simulate the nonlinear relationship between input and output variables. The model’s input variables can be a variety of elements that affect battery performance, while the model’s output variables include battery state characteristics including SOC, remaining useful life (RUL) and capacity.
This framework consists of three steps: data pre-processing, training and estimation.
4. Battery Parameters Extraction Techniques Using Grey Box Modelling Data-Driven Approach
Bio-inspired algorithms have also been extensively researched in recent years owing to their versatility and ease of implementation [87]. To model a battery, the internal circuit parameters need to be estimated. Estimation of these parameters is difficult due to their non-linear behaviour. The battery modelling (BM) problem is a constrained, multi-dimensional, mixed variable, non-convex, non-linear optimisation problem. Many bio-inspired techniques have been successfully employed to estimate the battery parameters [9,16,89,90]. When bio-inspired algorithms are implemented for COM to extract parameters in real time [9], then they are called grey box models. BM stands as a complex iterative procedure, and such complex associated BM analytical calculations are not handled accurately by the derivative-based methods and thus, the optimal solution is not guaranteed by the analytical methods. Apart from the deterministic methods, derivative free soft computing techniques such as GA are needed for the parameter identification to identify the optimal values for the polynomial coefficients of battery parameters of RC model [9]. This type of method is generally called bionic intelligent optimisation algorithms. Compared to all other methods, this technique has obvious advantages in accuracy and reliability, and it has become a popular method for parameter identification [91].
The battery modelling problem is also treated as a bi-objective optimisation problem in most of the recent research. Two objectives such as discharging terminal voltage and surface temperature are minimised using non-dominated sorting GA (NSGA) for lithium-ion batteries. Identified parameters of the P2D electro chemical model can indicate battery internal characteristics accurately, but the charging scenario, ageing mechanism and COM are not analysed. A multi-objective optimisation approach is also applied for COM parameter identification treating charge/discharge data at different currents [92,93,94,95,96].
Direct measurement EMF method is used to determine the state of charge of NiMH batteries for electric cars by employing first and second order equivalent circuit models. Results show that the precision of the second order model is higher than the first order model [78]. A systematic comparative study of various equivalent circuit models, i.e., twelve lumped COMs, was conducted for parameter optimisations [75]. On model comparison, it is suggested to prefer a lower order RC battery model, since other n-order RC models [32] are found expensive, complex and more susceptible to uncertainties [15]. Battery models that are accurate and simple are preferred.
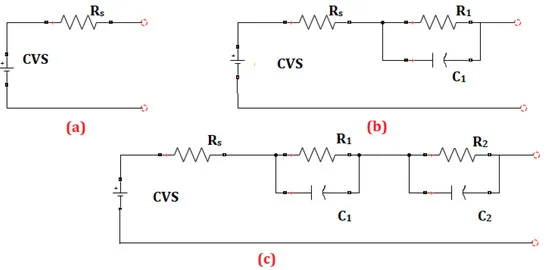
In Figure 1 , RS is the total resistance of the two electrodes, electrolytes and contacts. The transient behaviour of the battery is characterised using R1, R2, C1 and C2. Two RC networks having the time constants τ1 = R1 × C1 and τ2 = R2 × C2 (in the order of seconds and minutes, respectively) are used to depict the internal charge distribution of the battery. Constant voltage source (CVS) represents for the battery’s internal voltage source, which is modelled as the battery’s open circuit voltage (OCV) characteristics. CVS and OCV have been demonstrated to differ experimentally based on the amount of current.
This entry is adapted from the peer-reviewed paper 10.3390/su131810042
