Cell-to-Cell Communication and Information Transfer

Cell-to-Cell Communication and Information Transfer: History

Please note this is an old version of this entry, which may differ significantly from the current revision.

Subjects: Physics, Atomic, Molecular & Chemical

Contributor:

Crucial events are generated by criticality, namely by the processes of phase transition from disorder to correlated disorder, affecting key organismal network functions. There is, as suggested by, “a subtle connection between informational exchange within and between networks and the complexity (non-simplicity) of those networks”. West and Grigolini replaced the term complexity with non-simplicity and explain their reasoning by stating that in physics it is easier to understand how phenomena function by the properties or characteristics that are missing, rather than those that are present.

complexity
non-crucial events
crucial events
FBM
memory
embryos
seeds
development

1. Introduction

In physics, a system is considered complex if it meets the anti-reductionist criterion of “the whole being greater than its parts”, but as Melanie Mitchell states in Complexity , there is really no quantitative definition of complexity [19], and certainly not one upon which physicists, computer-, or biological scientists agree. There does seem to be agreement that living systems exhibit complex, changing behavior at the whole organism level (macrodynamics). This complex organismal behavior emerges from the collective actions and interactions at lower levels of organization, such as among cells (microdynamics). These actions can be understood using dynamical systems theory, which can be described simply as dynamic, i.e., systems that change over time (e.g., heart beats, firing of neurons in the brain, economic markets, or global climate). Developing systems also change in space as well as time and exhibit dynamic patterns of complexity, which adapt in response to learning or external forces. For example, increasing temperature will alter rates of development and growth in fish embryos, expressed as changes in morphological [20,21] and physiological [22] complexity. Complex adaptive systems, therefore, are complex systems exhibiting nontrivial emergent and self-organizing behaviors [19], many of which result from cell-to-cell communication at many developmental levels.

2. Exploring Criticality in Developing Organisms

It is our assertion that the stable yet dynamic society of a developing organism (i.e., plant seedling or animal embryo) results from, or may be initiated by, the dynamic interplay between two patterns of information exchange or complexity. These two patterns are, (1) self-organization or non-crucial events (Fractional Brownian Motion, FBM) [28] and (2) crucial events (defined as events that determine the efficiency of information exchange [7,15,29]. The type of response depends on the interplay of a network of intracellular (within a single cell) and/or intercellular (between cells) communication and their emergent relationships with their surroundings.

Much of what we know about patterns of complexity has been learned from long time series generated from electroencephalographs (EEGs) of firing rates in the human brain [30,31], heart rate variability [24], and swarming birds [8,32,33] among others. In all these examples there are elements of nonlinear interactions, which result in measurable patterns and modes known as phase transitions where there is a dynamic balance between order and randomness, and crucial events. Crucial events in the above situation are also referred to as renewal events, which are events that reset the memory of the system, erasing the memory of, and independent of, earlier events [15,29,31].

Many complex processes can be characterized by crucial or renewal events and all are independent of the underlying microdynamic emergent behaviors that can be localized in time. In [6] the authors clearly laid out that probability distribution densities (pdd) of the time distance, between two consecutive renewal events, which is given by the waiting time distribution ψ τ and written as an inverse power law,

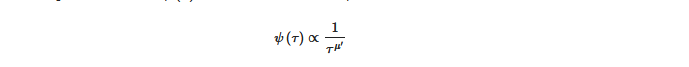
where μ is the complexity index which can range from 1 to ∞ , with complexity occurring when 1 < μ < 3. The breakdown in the ergodicity of a complex system for μ < 2 is a direct result of the occurrence of crucial events. However, if an event occurs at a specific time, after which subsequent events are produced, it is time dependent and the ψ τ has a hyperbolic form, see [15] for a more detailed discussion. As is stated in [6] μ < 3 suggests a departure from the condition of ordinary statistical physics to nonlinear statistical physics. Further, crucial events can arise spontaneously in complex systems, in keeping with the theory of self-organized temporal criticality (SOTC) [7,9,34,35,36] which posits that a system of interacting units may spontaneously generate temporal complexity, that is self-organized criticality (SOC) characterized by crucial events in time [6] in which μ is not limited to merely the non-ergodic regime of μ < 2 but extends to the whole complexity range of 1 < μ < 3.

In a developing organism, formation of an orderly multicellular network from relatively homogenous material in a single cell is the result of transactions among nonlinear, self-similar and self-organized components. Those transactions are generally known as cell-to-cell communication and operate based on an inducer (e.g., a cell that produces a signal) and a responder (a cell that responds to the signal by changing some behavior). Successful communication takes place when competence occurs, i.e., when a signal results in a response. We will now consider the processes that are understood to regulate cell-to-cell communication and highlight some of the gaps. These gaps in knowledge about cell-to-cell communication may be where information transfer and crucial events could play a part in directing development of coordinated causal multicellularity.

3. Cell-to-Cell Communication, Complexity and Self-Organization

While development is a process that occurs in all organisms, it is concerned with more than just cellular differentiation because different cell types of an organism do not exist in random arrangements. In the mid-twentieth century two biologists, Townes and Holtfreter [37] predicted that embryonic cells could have differences in the components of their cell membranes which allowed them to form organs. Now we understand that formation of organs is a result of cell-to-cell communication achieved through biochemical molecules that are secreted or located in the cell’s membrane. These ‘informational’ molecules can bind to receptors on neighboring cells and stimulate a signaling cascade of intracellular reactions, which results in changes in gene expression, enzymatic activity, and cytoskeletal organization, affecting cell shape and cell behavior. However, it should be mentioned that even at the biochemical level, cell-to-cell communication is much more complicated than suggested above. In addition to signaling cascades with the cell, there are also important intercellular secretory products that trigger cellular responses. These responses are typically ligand–receptor based and range from long distance (endocrine) hormones that travel through the blood stream to short distance (paracrine factors e.g., FGFs) that diffuse between cells across the extracellular matrix (ECM) to target receptors on the cell membrane. Also important to cell-to-cell communication are adhesion molecules that mediate the interactions between cells and the ECM, are critical for maintaining cell structure and function, and are key to organization of cells into tissues and organs.

Following fertilization, the process of cleavage transforms a single cell into a multicellular organism containing hundreds of cells (e.g., the nematode worm C. elegans contains 946 cells) or trillions of cells in an adult human being. These different cell types then work together to form a biologically complex, coherent, functional organism that can respond to change and exhibit a degree of resilience [38]. Physical (free diffusion, osmosis, viscosity, elasticity, and viscoelasticity) and cellular processes (mentioned above) act on single cells and take part in acts of aggregation and adhesion to form multicellular systems (tissues) and in the process they ‘re-enact ’ the development of cell-to-cell communication systems that emerged 1.5 billion years ago [38]. This means biochemical and energetic processes involved in cell-to-cell communication that first evolved 1.5 billion years ago are conserved, remaining essentially unchanged over evolutionary time. This then begs the question that if there are, as we suggest in this paper, informational exchange mechanisms also critical for development, might they too also have been conserved? During later stages of development, when organization of tissues and organs is taking place, the embryo stays in a relatively stationary state of reduced information (entropy) exchange that is maintained for extended periods of time, making self-organizing or autopoesis of living matter possible [39]. Autopoesis is understood to be any increase in the order within the system (i.e., production of negentropy) and is possible only if high internal biological organization through cell-to-cell communication exists [40].

Kauffman, in his landmark paper [41] stated that a fundamental task of biology is to account for the origin and nature of metabolic stability in living systems in terms of the mechanisms that control biosynthesis. Kauffman stated that biosynthesis includes the renewal or new production of cells resulting from a state of disorder through mitosis (which includes both DNA replication and cell division). He goes on to contrast order and chaos as interpreted in physics and then in biology. In physics when considering the thermodynamics of gases, the mathematical laws of statistics bridge the gap between the randomness of colliding molecules and the simplicity of the gas laws. Whereas in biology a gene can specify a protein and that protein can, in turn, control the expression and or repress another gene [42]. In living organisms, mathematical laws also engage large networks (referred to as gene regulatory networks (GRNs)) of interacting genes to bring biosynthetic or biological self-organization from disorder.

Waddington used the stability landscape to describe the cellular development where the cell was represented as the ball at the top of the landscape ( Figure 2 ). The paths available to the ball (or features of the landscape) are determined by the genotype, interactions among cells, tissues, organs, and the environment [8,49], forming what is referred to as the epigenotype (epi- or above-the-genotype). Epigenetics can include all effects and modifications that are dependent on genetic factors, such as DNA sequences, but may increase or decrease phenotypic (observable traits) variation expressed by target sequences in response to environmental cues, or emergent interactions during development [50,51]. The epigenotype can integrate information from external sources and influence development to produce a cohesive (coherent or stable) organism that will adapt to its environment by responding to change.

4. Measuring Complexity Using Ultraweak Photonic Emission (Upes)/Biophotons

Fröhlich [52] argued that organisms are made up of strongly dipolar molecules packed densely together in a ‘solid state’ in which electric and elastic forces will constantly interact. Macromolecules such as proteins, nucleic acids, and cellular membranes vibrate at characteristic frequencies [53] that result from the coupling of electrical displacements to mechanical deformations. Collective modes (coherent excitations) of electromechanical oscillations (phonons, or sound waves in a solid medium) and electromagnetic radiations (biophotons) that result that can extend over macromolecular distances within an organism [39]. Despite knowledge of these alternative ‘communication’ processes, few other ways have been considered important for cell-to-cell communication pathways in organisms until recently when biophoton research proved useful in human health monitoring [54] as well as identification and treatment of disease, especially cancer [55].

As sometimes happens in science, increasing interest especially for the treatment of human disease re-discovers work completed much earlier. This is the case with biophotons. In the 1920s Alexander Gurwitsch had already turned developmental biology on its head looking for top-down control of embryogenesis using what he referred to as “mitogenetic radiation” (biophotons), and then his work faded into the background. Almost a hundred years after Gurwitsch [56] first reported his “mitogenetic radiation” and the first case of non-chemical distant interactions, in a recent comprehensive review, Volodyaev and Beloussov [57] brought together data collected over the intervening century on biophotons, also known as ultraweak photonic emissions (UPEs). They reached two conclusions, (1) that the UV fraction of UPEs are regarded as real and, (2) the biological effects are difficult to reproduce reliably. While the review [57] does an admirable job of collecting together much of the empirical data on biophotons, some which are supportive of the mitogenetic effect (MGE), there appears to be some ambiguity about the usefulness of biophotons as a non-invasive method for research in biology and medicine and for their importance as a diagnostic tool for health assessment.

Instead of focusing on biophotons as a diagnostic tool for human disease we continue the good work of [57] and highlight new ways in which biophotons can help reveal the very nature of the beginnings of life. Here we highlight the work of [6] and the importance of using biophotons in conjunction with DEA as tools to detect and monitor changes in patterns of complexity over time, especially in a developing organism (a lentil seed). In 1923, Gurwitsch knew that in embryonic development, the number of cells increased as they divided. He wondered what triggered the cells to reproduce in the first place and, through observation, came to the conclusion that there must be coordinated external (environmental) and internal (cellular) events [56]. If this were true then the cell membrane must contain structures, what he called “receptors” that would perceive, and more importantly, convey a signal for a response. Today we describe the conveyance of a signal, as being part of a signal transduction system and these systems, like those of exchange mechanisms, have been conserved over evolutionary time for cellular communication [10]. Yet, the external stimulus that would initiate cell division was unknown until Gurwitsch [56] referred to one form of this information transfer as mitogenic radiation. Most of this understanding resulted from his famous onion tip experiment in which cells in the apical meristem or root tip of the onion seemed to increase the rate of cell division of a neighboring root tip. Gurwitsch suggested that such mitogenetic radiation acted as a non-mechanical deterministic principle in mitosis setting up a field of biophotons. This field resulted in changes in mitotic activity including molecular interactions within the cell cycle and, in fact, Gurwitsch had identified a type of matter and field dualism. In [5] Van Wijk later referred to this interplay between fields and matter, as a substance/field dualism, which in a biological system is based on its associated radiant (electromagnetic) structure, a stationary field obtained by superimposition of all fields associated with sub-systems, where interferences of oscillations are one process of conserving information (in the case of biophotons it is an optical code). The generation of codes associated with information in relation to interference and resonance are pivots for creating complexity, order and organization.

In [6] Benfatto et al., have for the first time correlated biophoton emission rates with changes in developmental organization (lentil germination) using photomultipliers in an experimental technique to detect low intensity photons with a small signal/noise ratio. Benfatto [6] first measured the dark count without seeds in the chamber, obtaining a baseline emission rate and then measured the biophoton emission counts with the seeds in the chamber continuously over a period of 72 h (Figure 3). Using the technique of DEA, dark count could be described by ordinary scaling, suggesting that no patterns of complexity were present in the absence of the seeds in the chamber (Figure 3). Without seeds in the chamber and in the dark a monotonic decrease in photon emission occurred a few hours after closing the chamber to detector noise, due to a reduction from the residual luminescence from exposure to light of the chamber materials (cotton bed and Petri dish) during experimental set-up. In the presence of seeds (n = 75), but still in the dark, the photomultipliers picked up a wide range (or bunch-type structure) of biophoton emissions per measurement. The bunch type nature resulted from an experimental artifact from the filter wheel (see [6] for experimental details) which stayed in each position (the wheel contains seven different filters) for one minute producing a bunch of emissions per filter every 443 s. It is also possible that the scattering per filter reading was also due to the range of different rates of development within the seeds during germination as well as variation in the timing of radicle (tap root tip) emergence (Figure 3).

Figure 3. Graph shows the signal or counts of biophotons vs time (h) generated by lentil seeds (n = 75) within a dark chamber (see [6] for experimental set-up). Raw data are shown, seeds (green) and dark counts (red) and the time averaged raw counts over one minute are shown. Vertical lines represent six regions (R1–R6) used in the DEA analysis. Middle panel shows artist’s rendering of lentil seeds before emergence of the radicle (tap root) (i.e., regions R1–3) which is the region of crucial events (orange arrow) and emergence and growth of radicle (i.e., regions R4–6) and region of non-crucial events or FBM (grey arrow). Figure is modified from [6].

Benfatto et al. [6] divided the total acquisition time during the experiment of 72 h into six regions for DEA analysis. In the first 30 h (regions R1–3, Table 1), DEA without using a technique called stripes (see [6] for equations) and showed that scaling parameters of the experiment had a mean ± SD (σ, SD = standard deviation) scaling index,

η

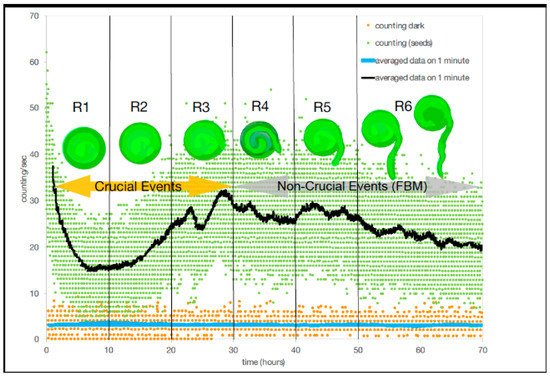
, of 0.77 ± 0.03 with a variance (σ²) of 0.001, which corresponded to a mean $μ$ = 2.30 ± 0.05 with a σ² of 0.002. While in the second set of three regions (regions #4–6, Table 1), there was a mean ± SD scaling index of $η$ of 0.72 ± 0.02 with a σ² of 0.0005, which corresponded to a mean $μ$ = 2.39 ± 0.04 with a σ² of 0.002. Thus, DEA without stripes could not distinguish between crucial events and FBM (Figure 3). In contrast, when applying the use of stripes to DEA, the results showed a clear and significant time dependence in the first three temporal regions where the mean scaling parameter of $η$ ± SD is 0.56 ± 0.04, and a variance of 0.001, which corresponds to a mean $μ$ ± SD, 2.79 ± 0.11 with a σ² of 0.012 (Table 1). While in the second three regions (regions #4–6, Table 1), there was a mean ± SD of the scaling index of $η$ of 0.503 ± 0.01 with a σ² of 0.00006, which corresponded to a mean $μ$ = 2.99 ± 0.03 with a σ² of 0.0007. For DEA with stripes, results indicated that crucial events exist in the first three temporal regions (#1–3) and non-crucial events dominate in the last three temporal regions (#4–6). Although, as Benfatto et al. [6] explained that there was the possibility of no crucial events and that anomalous scaling (with the significant difference from ordinary scaling $η$

= 0.5) is due to FBM. It is clear however, that no temporal complexity exists during the dark count part of the experiment compared to when the seeds were in the experimental chamber.

Table 1. The scaling factors obtained using DEA with and without stripes for six different regions of the total 72 h time series including with seeds and dark count regions. Regions 1–3 represent regions of crucial events, Regions 4–6 represent regions of FBM. Table modified from [6].

To examine the relationship of biological development of the lentil seeds with the recorded biophoton emission patterns and their implication for the existence of crucial events, we will propose that in the first three regions (#1–3) the lentil seeds are undergoing internal preparations with the cell cycle for germination. During this time, each seed uses the energy store or cotyledon within the seed to prepare for germination by replicating DNA as part of the cell cycle (S phase) and these may result in state changes, which generate crucial events (in the first regions). After this, which cell-division (M-phase) occurs with the emergence of the radicle (tap root) (germination) (in the last three regions), when crucial events were not detected.

In short, this landmark work from Benfatto et al. [6], is the first empirical data gathered to show that the developmental process of germination of lentil seeds is a process that has phase transitions accompanied by changes in patterns of complexity (crucial to non-crucial events). Past work using biophotons to detect changes in developmental processes has been shown in yeast growth, with biophoton intensity being higher during DNA replication (S-phase) than during cell division (M-phase) [58] and in wheat seeds [59]. However, in both cases it was not possible to distinguish if different patterns of complexity existed because DEA was not applied to their data. Benfatto et al. [6] concluded that using DEA as the statistical analysis in conjunction with changes in biophoton emissions suggests that criticality appears to be an important factor in the transmission, transfer and coding of information important to multi-component processes in living organisms, such as germination in plant seeds. These results offer the possibility of using biophoton and DEA in experiments to investigate the existence of variation in complexity patterns in a variety of different developing organisms. Further, these data provide evidence for the importance of the exchange of information (entropy) transfer for cell-to-cell communication during organismal development.

This entry is adapted from the peer-reviewed paper 10.3390/e23091141

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.