1. Introduction

The main characteristics of an MIR laser can be summarized as the following two aspects. First, as the pondermotive energy is quadratically proportional to the driving laser wavelength, MIR lasers with high peak power have been routinely pursued as the driving sources for novel strong-field phenomenon [1,2,3,4,5,6,7,8,9], such as extreme ultra-violet and X-ray generation [10,11,12,13], attosecond pulse generation [14], and terahertz generation [15,16,17]. Second, most of the vibrational peaks of different molecules fall in the MIR band, which is also called the “molecular fingerprint” regime. Therefore, MIR coherent spectroscopy is a unique method for high-fidelity and high-sensitivity molecule detection and identification [18,19,20,21,22,23,24].

As for MIR solid-state lasers, there are two main technique streams to generate MIR pulses, namely the direct emission of doped ions and optical parametric down conversion. The former is based on a process wherein the gain medium is stimulated after energy storage, and the output wavelength depends on the energy level structures of the gain media. The biggest challenge of this process is that the relaxation energy in the MIR wavelength coincides with the phonon vibration energy, which reduces the gain and hinders the lasing process at the MIR wavelength. The second technique is based on the parametric frequency conversion that is mainly assisted by nonlinear crystals that create the phase-matching conditions. In this process, there is no thermal accumulation, and broadband laser amplification can be realized through broadband phase matching, which supports the generation of few-cycle MIR pulses. At present, parametric down conversion has become an indispensable means to expand the new laser spectrum, generating pulses covering deep ultraviolet, visible, near-infrared, MIR, and THz wavelength regimes.

2. MIR Nonlinear Crystals

Nonlinear crystals that are commonly used in MIR pulse generation and amplification mainly include KTiOAsO₄ (KTA), KTiOPO₄ (KTP), and LiNbO₃ (LNO), which belong a group known as oxide crystals, and ZnGeP₂ (ZGP), CdSiP₂ (CSP), AgGaS₂ (AGS), AgGaSe₂ (AGSe), GaSe, BaGa₄S₇ (BGS), BaGa₄Se₇ (BGSe), LiGaS₂ (LGS), and LiGaSe₂ (LGSe), which are classified as non-oxide crystals. Generally, the damage threshold and mechanical hardness of oxide crystals are excellent, but their transparent range is limited to less than 5 µm, which is not conducive for the generation of long-wavelength MIR pulses. The effective nonlinear coefficient of non-oxide crystals is higher, and the transparency range can reach more than 10 µm, which is commonly used in the generation of long-wavelength infrared pulses. However, the bandgap energy of such crystals is generally around 2 eV, which makes the two-photon absorption non-negligible, and significantly reduces the damage threshold when pumped at an ~1 µm wavelength with high peak power. LGS and LGSe are relatively new MIR nonlinear crystals with large bandgap energy, which enables high peak power pump at an ~1 µm wavelength. However, the transparent range of LGS and LGSe are limited to 10 µm. High quality new MIR nonlinear crystals with large bandgap energy and a broader transparent range are desired. BGSe is one of the candidates, however, the crystal growth quality still needs substantial improvement. In addition to the above MIR nonlinear crystals, periodically poled crystals such as periodically poled LiNbO₃ (PPLN), orientation-patterned GaAs (OP-GaAs), and orientation-patterned GaP (OP-GaP) have become an emerging stream in the MIR parametric down conversion with their excellent quasi-phase matching bandwidth and large nonlinear coefficients, although their aperture size is the current bottleneck for pulse energy upscaling.

3. MIR Generation

Among all kinds of nonlinear polarizations, the most commonly used in down conversion is probably the second-order nonlinear effect due to the good efficiency. The three-wave mixing process introduced by the second-order nonlinear effect is the basis of second harmonics generation (SHG), difference-frequency generation (DFG), and OPA. DFG and OPA are the main methods of broadband MIR pulse generation and amplification. In a further step, combined with the theory of OPA and chirped-pulse amplification (CPA) technologies, OPCPA have emerged to scale up the pulse energy and peak power of MIR few-cycle lasers.

3.1. OPA

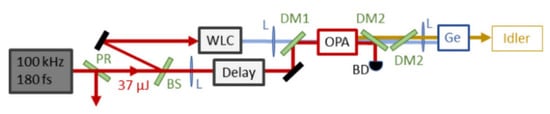
OPA is an old parametric technique with emission in the visible and near-infrared wavelength regimes. It has the merits of broadband emission and simple dispersion control. Recently, the OPA emission bad has been extended to MIR wavelengths pumped at ~1 and ~2 µm wavelengths, as summarized in Table 2.

Figure 5. Illustration of BGS OPA laser system. BS, beam sampler; PR, partial reflector; WLC, white light continuum generation unit; L, lens; BD, beam dump. DM1, dichroic mirror, high reflection (HR) at 1.03 µm and high transmission (HT) at >1.1 µm; DM2, dichroic mirror, HR at 1.0–1.2 µm and HT at 6–12 µm; OPA, LGS or BGS crystal; Ge, germanium-based temporal chirp compensation unit. Reprinted with permission from [33].

3.2. MIR OPCPA

3.2.1. 2–4 µm OPCPA

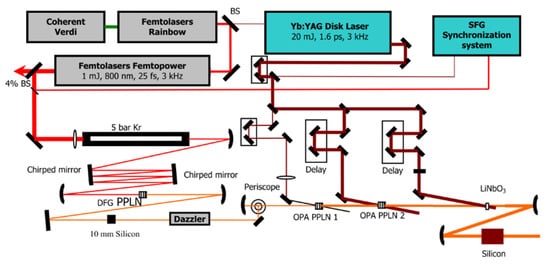
OPCPA systems have superior energy and power upscaling capability. With careful dispersion management, amplified pulses with a pulse width close to the transform limit could be generated. High-energy, few-cycle light sources with a central wavelength of 2–4 µm, and multi-millijoule pulse energy have been realized in many research groups via OPCPA techniques. Table 3 summarizes the specifications of few-cycle 2–4 µm OPCPA.

Table 3. Parameters of selected 2–4 µm OPCPA system.

Wavelength (µm)	Pulse Energy (mJ)	Repetition Rate (kHz)	Power (W)	Pulse Width (fs)	Optical Cycle	Reference
2.1	1.2	3	3.6	10.5	1.5	[39]
2.1	2.7	10	27	30	4.3	[40]
2.1	2.6	1	2.6	39	5.6	[41]
2.2	0.25	100	25	16.5	2.2	[42]
2.5	0.126	100	12.6	14.4	1.7	[43]
3	0.3	10	3	21	2.1	[44]
3	2.4	10	24	50	5	[45]
3.07	0.01	125	1.25	72	7	[46]
3.1	0.125	100	12.5	73	7	[47]
3.2	0.152	100	15.2	38	3.6	[48]
3.25	0.06	160	9.6	14.5	1.4	[49]
3.4	0.012	50	0.6	41.6	3.7	[50]
3.425	13.3	0.01	0.133	111	9.7	[51]
3.9	8	0.02	0.16	83	6.4	[52]
4	2.6	0.1	0.26	21.5	1.6	[53]

In a pioneer work, F. Krausz’s research group employed the broadband Ti:sapphire laser (oscillator and amplifier) as both the signal and pump at the same time [39]. As shown in Figure 6, the 1030 nm component of the broadband spectrum output from the Ti:sapphire oscillator was extracted and injected into a Yb:YAG thin disk amplifier to obtain the pump light synchronized with the signal beam. Non-collinear OPAs (NOPAs) were carried out in two stages using PPLN crystals and during the last power amplifier stage with a LNO crystal. Finally, a MIR output at a central wavelength of 2.1 µm and a repetition frequency of 3 kHz with a pulse energy of 1.2 mJ and a pulse width of 10.5 fs (1.5 cycles) was obtained.

Figure 6. Schematic of 2.1 µm few-cycle OPCPA system. Reprinted with permission from [39].

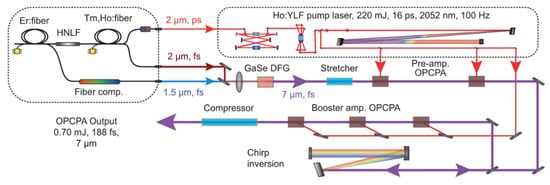
3.2.2. 5–10 µm OPCPA

In recent years, there have been emerging reports of long-wavelength MIR OPCPA systems with lasing wavelengths exceeding 5 µm. Table 4 summarizes long-wavelength MIR OPCPA systems with the centre wavelengths of 5 µm, 7 µm, and 9 µm.

Table 4. Parameters of the long-wavelength MIR OPCPA systems.

Wavelength (μm)	Pulse Energy (mJ)	Repetition Rate (kHz)	Power (W)	Pulse Width (fs)	Optical Cycle	Reference
5	3.4	1	3.4	89.4	5.4	[54]
7	0.7	0.1	0.07	188	8	[55]
9	0.014	10	0.14	142	4.7	[56]

In 2016, J. Biegert’s team demonstrated a high-energy, few-cycle 7 µm OPCPA [55]. As shown in Figure 13, the system started with an Er:Tm:Ho:fiber laser which generated a 7 µm seed via DFG in a CSP crystal. The 7 µm seed pulse was then amplified in a ZGP-based OPCPA chain pumped by a cryogenic-cooled Ho:YLF CPA system with a 260 mJ pump energy at 2052 nm and a 16 ps pulse width. The pulses were first put through both a pre-amplifier and booster amplifier stage, and finally put through a compressor, after which a 7 µm pulses with a 0.75 mJ pulse energy and a 188 fs pulse width were obtained.

Figure 13. Layout of the 7 µm OPCPA. The MIR seed was generated using the two broadband femtosecond outputs from a three-color fiber frontend via DFG. Afterwards, the MIR pulses were stretched in a dielectric bulk and consecutively amplified in a pre-amplifier and a booster amplifier separated with a chirp inversion stage. Maximum efficiency of the OPCPA was achieved by tailoring the seed-to-pump pulse durations in the pre-amplifier and booster amplifier. The broadband high-energy MIR pulses were recompressed using a dielectric bulk rod of BaF₂. Reprinted with permission from [55].

3.3. MIR Intra-Pulse DFG

DFG has remarkable advantages such as a single pass structure without complex cavity adjustment and a broad tuning range of the output spectrum. Intra-pulse DFG (IPDFG) is a special DFG process that uses the low and high frequency components of an ultra-broadband pump pulse to realize MIR femtosecond emission. In this method, only an ultra-broadband pump laser with a few-cycle pulse width is needed, which further simplifies the DFG process. Table 5 lists the state-of-the-art work that have generated few-cycle MIR laser pulses.

Table 5. Parameters of selected IPDFG source.

Pump Wavelength (µm)	Nonlinear Crystal	IPDFG Spectral Span (µm)	Conversion Efficiency (%)	Reference
1.03	LGS	8–11	0.037	[58]
1.03	LGS	6.8–16.4	0.11	[59]
1.57	OP-GaP	4–12	0.071	[24]
1.9	GaSe	3.7–18	1.4	[60]
2	ZnSe	2.7–20	0.51	[61]
2	GaSe	4.5–20	0.13	[62]
2.1	AGSe	7–11	0.8	[63]
2.5	GaSe	4.3–17.6	0.22	[64]
2.5	ZGP	5.8–12.5	3.3	[64]
3	GaSe	6–13.2	5.3	[65]

J. Zhang et al. demonstrated few-cycle pulse generation by means of the soliton self-compression of the pump pulse in a silica-core photonic-crystal fiber, and subsequently, LWIR generation using IPDFG, resulting in a two-octave-spanning spectrum (−30 dB) from 5 to 20 µm at an average power of 24 mW, as shown in Figure 17 [62].

Figure 17. (a) Self-compression and MIR generation setup. (b) MIR spectrum and beam profile. The MIR spectrum (red line) together with the noise floor (gray line) measured using a monochromator. The MIR spectrum extends from 500 cm⁻¹ to 2250 cm⁻¹ (−30 dB), corresponding to the wavelength range from 4.5 to 20 µm. Inset: the beam profile measured using a Pyrocam beam profiler. Reprinted with permission from [62].

4. Single-Cycle MIR Generation

High energy single- or sub-cycle MIR pulses can provide unique opportunities to explore phase-sensitive strong-field light-matter interactions in atoms, molecules, and solids. Tremendous efforts have been made to reduce the duration of a laser pulse down to a few-cycle or to the single-cycle regime. Obtaining such an ultrashort laser pulse requires spectral broadening and phase control over the ultrabroad spectrum that supports a single-cycle pulse. At present, four methods have been used to generate single-cycle MIR pulses, namely DFG, four-wave mixing (FWM), OPA, and IPDFG. Table 6 shows several works that have generated single- or sub-cycle MIR pulses.

Table 6. Parameters of single- or sub-cycle MIR.

Method	Wavelength (µm)	Repetition Rate (kHz)	Pulse Energy (µJ)	Pulse Width (fs)	Optical Cycle	Reference
DFG	5–300	1	0.4	46	1	[67]
	3–18	1	2	45	1.2	[68]
	1.8–4.4	1	1.5	11	1.2	[69]
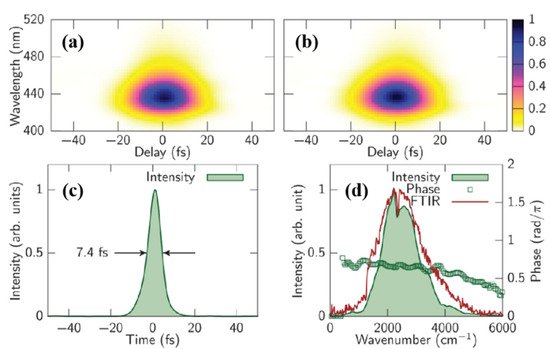
FWM	2–20	1	0.25	7.4	0.57	[70]
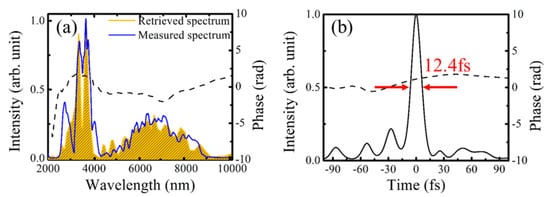
OPA	2.5–9	1	33	12.4	0.88	[35]
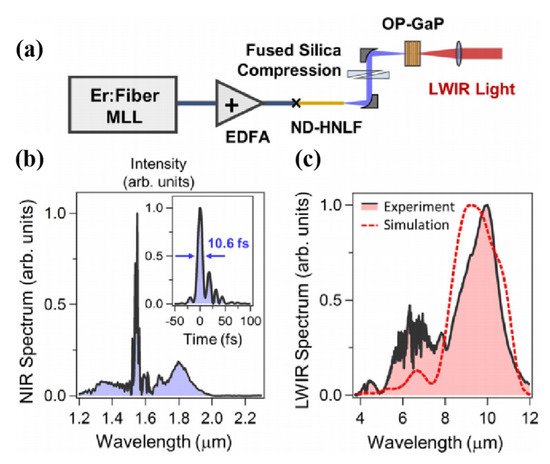
IPDFG	4–12	1 × 105	2.5 × 10−6	−	−	[24]
	6–18	5 × 104	0.01	43	1.16	[71]

4.1. MIR Single-Cycle Pulse Generation via DFG

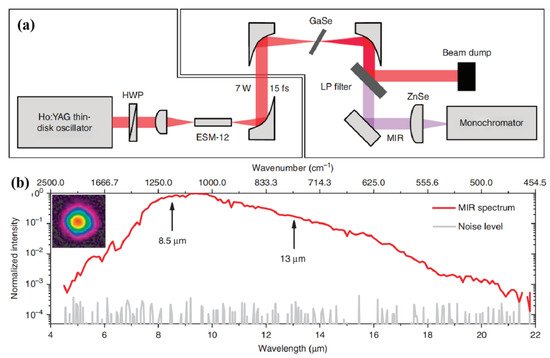
In 2015, A. A. Lanin et al. presented a MIR transient centered at a wavelength of 7.9 µm with the pulse width of 45 fs (~1.2 cycle) and the spectrum ranged from 3–18 µm at 1 kHz repetition rate [68]. As shown in Figure 21, first, a seed produced by supercontinuum in a sapphire plate, which was driven by 810 nm, 0.8 mJ, 65 fs, 1 kHz pulses delivered by a Ti:sappire laser. This seed was sent to an OPA with a BBO crystal, generating tunable signal and idler pulses that ranged from 1150–1580 nm and 1620–2300 nm, respectively. In the second step, the signal and idler from the OPA were used for DFG in an AGS crystal, producing a MIR pulse with a pulse duration of 150 fs and pulse energy of ~2 µJ at the central wavelength of 7.9 µm. After that, the MIR radiation underwent spectral broadening and self-compression in a 5 mm GaAs plate with high nonlinearity, leading to a spectrum covering 3–18 µm, and the pulse width compressed into 45 fs.

Figure 21. Experimental setup. Ti:S, mode-locked Ti:sapphire master oscillator; MPA, multipass amplifier; OPA, optical parametric amplifier; AGS, AgGaS₂ crystal; LPF, longpass filter; PM, parabolic mirror; L, BK7 glass lens; OD, optical delay line; PMH, parabolic mirror with a hole; FWM, four-wave mixing in a gas medium; SPF, shortpass filter; Spec, spectrometer. Reprinted with permission from [68].

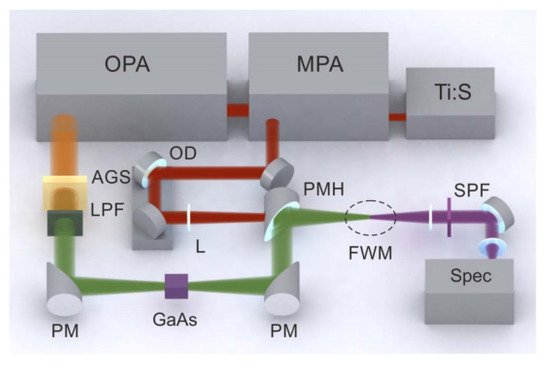
4.2. MIR Single-Cycle Pulse Generation via FWM

In 2012, Y. Nomura et al. investigated MIR sub-cycle pulse generation via FWM. The fundamental mode and second-harmonic pulses of a 25 fs Ti:sappire amplifier output with the wavelength of 800 nm and energy of 0.9 mJ at 1 kHz were focused into argon gas, producing a phase-stable sub-cycle MIR pulse through FWM assisted by filament [70]. As shown in Figure 23, a phase-stable 250 nJ, 7.4 fs (0.57 cycles) MIR conical emission centered at 3.9 µm with its spectrum coverage of 2–20 µm was created.

Figure 23. (a) Experimental and (b) retrieved XFROG traces. The retrieved pulse in (c) time and (d) frequency domain. The spectrum measured with Fourier transform spectrometer (brown solid curve) is also shown. Reprinted with permission from [70].

4.3. MIR Single-Cycle Pulse Generation via OPA

In 2017, H. K. Liang et al. generated a MIR sub-cycle pulse from an OPA with the signal and idler pulses at 3.2 µm and 6.4 µm [35]. It was demonstrated that with the stable carrier-envelope phase for both the signal and idler pulses and the careful control of the relative delay, the signal and idler pulses were synthesized without extra coherent control. As shown in Figure 24, the synthesized pulse had a spectral coverage from 2.5 to 9.0 µm, and a pulse width of 12.4 fs which corresponded to 0.88 cycles for a central wavelength of 4.2 µm.

Figure 24. Temporal characterisation of the synthesised MIR pulse. The retrieved spectral (a) and temporal (b) intensity profiles of the synthesised pulse. The dotted curves are the retrieved phase. Pulse width (12.4 fs) at full width at half maximum is measured with a centre wavelength at 4.2 µm. It corresponds to 0.88 optical cycle. Reprinted with permission from [35].

4.4. MIR Single-Cycle Pulse Generation via IPDFG

In 2018, H. Timmers et al. presented a scheme for generating super-octave spanning MIR frequency combs with a bandwidth spanning from 4 to 12 µm through IPDFG in an OP-GaP crystal driven by a few-cycle Er-pump infrastructure [28]. As shown in Figure 25a, the output of an Er mode-locked laser was amplified using an Er-doped fiber amplifier. The amplified pulses then undergo nonlinear broadening in a nonlinear fiber and were compressed to a few-cycle pulse width serving as the pump of IPDFG. MIR radiation spanning from 4 to 12 µm was generated from an OP-GaP crystal. Subsequently, in 2019, from the same group, A. S. Kowligy et al. measured the temporal profile of the MIR pulse via electro-optical sampling using an ultra-short near-infrared reference pulse. A 1.2-cycle MIR pulse oscillating at a 7.6 µm centre wavelength was obtained [73].

Figure 25. (a) Experimental layout for IPDFG comb generation. (b) The spectrum of this few-cycle driver. The inset of (b) displays the measured intensity profile of the pump pulse, corresponding to a pulse duration of 10.6 fs. (c) Super-octave longwave infrared (LWIR) spectra containing up to 0.25 mW of power. Reprinted with permission from [24].

5. Prospects of High-Power Broad-Band Few-Cycle MIR Lasers

The development of high-power broadband few-cycle MIR lasers has been driven by a number of applications in the field of strong-field physics, high-fidelity molecule detection, and cold tissue ablation applications. In strong-field physics, high-order harmonic generation (HHG) with excellent spatial coherence is probably one of the biggest driving forces of strong MIR OPCPA. Extreme ultra-violet harmonics with the photon energy exceeding the water absorption window have been generated via the MIR OPCPA pump [17]. The famous 3.9 µm OPCPA has enabled the generation of soft X-ray HHG with the photon energy extended to 1500 eV. Besides HHG, femtosecond hard X-ray covering tens of keV photon energy has been excited through plasma generation in a metallic target, pumped by the MIR OPCPA [13]. Attosecond pulse generation is another main application of MIR OPCPA in the field of strong-field physics. A total of 40–50 as isolated attosecond pulses have been generated pumped by 1.8 μm OPCPA/OPA [1]. Moreover, terahertz generation with a high conversion efficiency of 2.36% has been achieved via MIR two-colour filamentation in air pumped by MIR OPCPA centred at 3.9 µm. Besides the peak power of the MIR OPCPA system, which sets the threshold and cut-off of the aforementioned strong-field applications, the average power is another important parameter to pursue, which accounts for photon flux. Therefore, it is suggested high-average power MIR OPCPAs with decent pulse energy be the next research phase focus serving as the enablers to reveal a more uncharted continent in the field of strong-field physics.

Molecule detection is another important application of MIR OPCPA. Laser filamentation in air pumped by energetic MIR OPCPAs has been realized at the 3.9 and 2 µm wavelengths [74,75]. Stand-off detection of ambient air molecules such as CO₂ have been demonstrated via air filamentation pumped using MIR OPCPA [22]. By using the atmospheric transparent windows in the MIR wavelength region, namely the 2–5.5 µm and 8–14 µm bands, more molecules in the air could be detected with MIR OPCPAs, especially at longer wavelengths such as 5 and 9 µm. In addition, dual-frequency combs (DFCs) based on broadband MIR lasers have been developed for sensitive and precision molecule sensing. With DFCs at the 3–5 µm wavelength range, the detection of molecular species in a gas mixture, including isotopologues containing isotopes such as ¹³C, ¹⁸O, ¹⁷O, ¹⁵N, ³⁴S, ³³S, and deuterium, with part-per-billion sensitivity and sub-Doppler resolution has been demonstrated [23]. At longer wavelengths covering 4 to 12 µm, DFCs have enabled the high-precision vapor detection of methanol and ethanol. With the high-average power of the MIR broadband laser sources at a 100 MHz repetition rate, a good signal-to-noise ratio (67 Hz^1/2) has been achieved with a sub-ms acquisition time.

Besides strong-field physics and spectroscopic applications, high-power, broadband, few-cycle lasers have also been used in minimally invasive surgery. However, limited by the available femtosecond laser wavelengths, its current applications in bio-medical micro processing/surgery are only limited to cataract surgery [76,77] and myopia correction surgery [78,79,80]. An MIR wavelength at 3–10 µm coincides with strong molecular resonant peaks, which results in strong and sharp absorption peaks for various molecules. The strong absorption resonances of water, protein, and lipids have been investigated using MIR femtosecond laser exposure from a free-electron laser facility in ocular, brain, and dermis tissues. A new mechanism for tissue ablation was proposed. It was found that when a MIR femtosecond laser at the 6.2–6.7 µm wavelength is chosen, the laser output power is absorbed by both water and proteins. Reaching ~60 °C, collagen undergoes structural transitions from highly ordered arrays to amorphous gelatin with less resilience, which enables better tissue ablation efficiency and less lateral damages. With the emerging and development of high-power MIR femtosecond lasers at more flexible wavelengths, we foresee promising prospects for watt-level MIR femtosecond lasers in the soft and hard tissue cold ablation applications.

This entry is adapted from the peer-reviewed paper 10.3390/photonics8080290