Colloidal metal nanoparticles in an electrolyte environment are not only electrically charged but also electrochemically active objects. They have the typical character of metal electrodes with ongoing charge transfer processes on the metal/liquid interface. This picture is valid for the equilibrium state and also during the formation, growth, aggregation or dissolution of nanoparticles. This behavior can be understood in analogy to macroscopic mixed-electrode systems with a free-floating potential, which is determined by the competition between anodic and cathodic partial processes. In contrast to macroscopic electrodes, the small size of nanoparticles is responsible for significant effects of low numbers of elementary charges and for self-polarization effects as they are known from molecular systems, for example. The electrical properties of nanoparticles can be estimated by basic electrochemical equations. Reconsidering these fundamentals, the assembly behavior, the formation of nonspherical assemblies of nanoparticles and the growth and the corrosion behavior of metal nanoparticles, as well as the formation of core/shell particles, branched structures and particle networks, can be understood. The consequences of electrochemical behavior, charging and self-polarization for particle growth, shape formation and particle/particle interaction are discussed.
- nanoparticles
- colloidal solutions
- electrical charging
- self-polarization
- mixed-electrode
- particle growth
- particle interaction
1. Introduction
Metal nanoparticles have attracted a lot of scientific interest in recent years. The most important practical motivations come from their interesting electronic and optical properties [1–4], their applicability for nanolabeling [5,6] and sensing [7–10] and their catalytic properties [11,12]. In addition, they are fascinating targets for basic research for understanding the nature of nano-objects and the interaction with biomolecules and living cells [13–16] and for designing new materials, as well as micro- and nanosized tools [17,18].
An important field of nanoparticle generation and handling is liquid-phase synthesis resulting in colloidal solutions of metal nanoparticles [19,20]. The existence of nanoparticles in the form of a thermodynamically stable dispersion in a liquid was firstly explained by Michael Faraday about one and a half centuries ago. Already at this time, the importance of the electrical properties of colloidal particles was recognized.
In addition to the presence of an electrical charge on metal nanoparticles, the exchange of charges and the interaction with ions are important for the generation and behavior of metal nanoparticles. Charge transfer processes can include the release of ions from the metal or the conversion of adsorbed metal cations into metal atoms. These processes, as well as oxidation and reduction reactions of other species, can be regarded as local electrochemical processes [21]. In the following, important examples of such processes will be regarded and discussed from the point of view of the electrode character of colloidal metal nanoparticles.
2. Formation of Colloidal Metal Nanoparticles by Reduction of Solution Precursors
In the past, the general model of LaMer [22] was frequently used for explaining the formation of nanoparticles in liquid media. This model postulates a two-step process, whereby in a first step, single atoms or molecules aggregate to form nuclei, and, in a second step, these nuclei grow by the attachment of further atoms or molecules, as long as the concentration of particle-forming species is above the critical saturation concentration. The concept of LaMer is based on the assumption that the critical concentration threshold for nucleation is significantly above the saturation limit. Thus, nucleation proceeds only at very high concentrations, which means in a short start phase, whereas particle growth can occur over a longer time until the exhaustion of particle-forming species above the saturation limit.
The LaMer model was not developed for the specific conditions for the reactive formation of metal nanoparticles by the reduction of a precursor. For the example of colloidal gold, it was shown by Polte et al. that the formation of spherical metal nanoparticles was caused by an aggregation and growth mechanism, which could be proved by in situ-X-ray scattering measurements [23]. The proposed mechanism of Polte et al. is very conclusive and also gives a convincing explanation for the polycrystalline character of spherical gold nanoparticles [24].
The start of reductive metal nanoparticle formation is a molecular process. The primarily formed products are clusters, and their nature is closer to small molecules than to a classical metallic solid. The simplest description is given by the following reaction equation:
|
Mn+ + n e− à M0 |
(1) |
The electrons are supplied from the oxidation of the reducing agent (RA):
|
RA à RAm+ + m e− |
(2) |
Both processes are coupled and can be written formally as a redox reaction:
|
Mn+ + n/m RA à M0 + n/m RAm+ |
(3) |
Single free metal atoms are usually not stable in a liquid environment. Thus, Equation (1) should be written better as forward and backward processes or as equilibrium:
|
Mn+ + n e− à M0 à Mn+ + n e− |
(4) |
Irreversibility is achieved if a stable cluster is formed consisting of a small number x of metal atoms; for example, z = 4:
|
z Mn+ + n×z e− à (Mz) |
(5) |
The above-written equations are a very formal description of the processes during the reaction of a metal precursor species in a polar solvent. It is to be assumed that the formation of clusters does not result in a neutral particle without any ligands. Instead, it has to be expected that the clusters are electrically charged and connected with ligands by analogy with the coordinatively bound or solvated metal ions of the precursor.
Metal ions are solvated or connected with ligands L in coordination compounds or complex ions. The primary formed cluster (Equation (5)) is also connected with ligands X, which can differ from the original ligands of the metal ion complex. The following equations give an example of how the formation of a stable cluster could proceed, whereby the electrons come from direct reduction by interacting molecules of the reducing agent, whereby noncharged ligands L and X and a single positive charge per metal ion are assumed, for simplification:
|
2[MLn]+ + e− à [M2L(2n-a)]+ + a L (reduction in solution) |
(6) |
|
[M2L(2n-a)] + b × à [M2L(2n-a-b)Xb] + b L (partial ligand exchange) |
(7) |
or
|
[M2L(2n-a)] + (2n-a) × à [M2X(2n-a)]+ + (2n−a) L (complete ligand exchange) |
(8) |
The following steps are written for the example without ligand (L by X) exchange:
|
[M2L(2n-a)]+ + [MLn]+ à [M3L(3n-a-b)]2+ + b L (metal ion adsorption) |
(9) |
|
[M3L(3n-a-b)]2+ + e- à [M3L(3n-a-b)]+ (reduction step) |
(10) |
|
[M3L(2n-a-b)]+ + [MLn]+ à [M4L(4n-a-b-c)]2+ + c L (metal ion adsorption) |
(11) |
|
[M4L(4n-a-b-c)]2+ + e− à [M4L(4n-a-b-c)]+ (reduction step) |
(12) |
and so on.
The equations above illustrate the alternation of steps of metal ion or complex, respectively, adsorption and reduction. It is not necessary to assume the formation of metal(0) atoms that have to aggregate spontaneously to form a nucleus that can subsequently grow. It is much more probable that there is a direct way from the formation of a coordinated cluster of very few atoms to a continuous growth process. This growth process is always composed of the reduction of adsorbed metal ions into metal(0) and the electron supplying oxidation of the reducing agent. From this point of view, there is no classical nucleation process, as postulated by the LaMer model. Instead of this, the reductive formation of metal nanoparticles can be described by the coupling of reduction and oxidation from the very beginning of the first metal–metal interaction.
After completion of the particle growth, the particles in a stable colloidal solution are in a thermodynamic equilibrium state. This means that cathodic and anodic elementary processes are further running but with equal rates in both directions. As a result, the surfaces of metal nanoparticles experience a fluctuation in the adsorption and release of metal ions, as well as in the oxidation and reduction of residual active redox species in solution. Each elongation of the thermodynamic equilibrium state—for example by changing temperature, pH, metal precursor, ligand or reducing agent concentrations—induces shifts in the intensity of the electrochemical processes on the particle surfaces and, therefore, changes in the size or shape of particles.
3. Forming Colloidal Metal Nanoparticles as Mixed-Electrode Objects
The reaction system of reductive metal nanoparticle formation consists of two different object types: the ion-containing solution with the character of an electrolyte and the metallic clusters and nanoparticles. Bulk metals and metal films and metal clusters are marked by high internal charge carrier mobility. This is the essential feature of the metallic state. Together with the electrolyte, an electrode is formed.
Each electrode is marked by its electrode potential. This potential can be measured, in principle, by the voltage between the electrode and a reference electrode. However, such a direct measurement is impossible in the case of nanoparticles.
The electrochemical potential of a metal particle during its formation results at least from the metal deposition and the oxidation of the reducing agent (RA). The metal reduction represents the cathodic partial process as formulated by Equation (1). The anodic partial process can be written as:
|
RA à RA+ + e− |
(13) |
Due to the, at least, two electrode processes, the particle is a mixed-electrode object (Figure 1). The absence of any outside current source means that this potential is only controlled by the ongoing electrode processes. Metal nanoparticles have a free-floating potential.
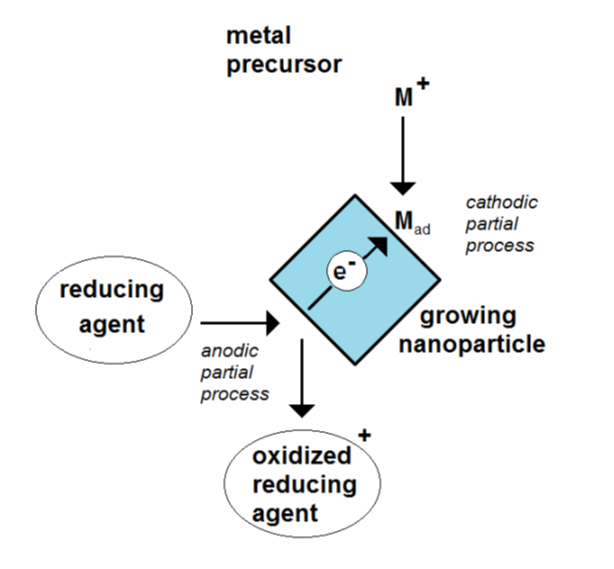 Figure 1. Scheme of the formation of an electrochemical mixed potential of a growing nanoparticle by the coupling of a cathodic and an anodic partial process.
Figure 1. Scheme of the formation of an electrochemical mixed potential of a growing nanoparticle by the coupling of a cathodic and an anodic partial process.
The potential of clusters and nanoparticles of z atoms Mz is modified, in addition, by the adsorption of ions, ligands and other reaction partners, for example by following ligand exchange reaction:
|
(MzLn) + X− à (MzLn-1X)− + L |
(14) |
The small size of nanoparticles causes a high sensitivity of the particle potential against the exchange of single charges. The clusters and the growing nanoparticles behave as electron confinements with a fluctuating potential. Each adsorption or desorption of an ion and each uptake or release of an electron changes the electrochemical potential. An increase in potential enhances the probability of oxidation of an adsorbed or colliding molecule of the reducing agent. A decrease in potential enhances the probability of metal deposition.
The order of magnitude of potential change by the transfer of one elementary charge qe can be estimated by regarding the particle surface as an electrical capacitor with the capacitance C, an electrode distance in the order of magnitude of the electrochemical double-layer thickness d and the surface area A:
|
C = ε0 × εr × A/d |
(15) |
The stored charge on such a capacitor Q depends on the capacitance and the voltage:
|
Q = C × U |
(16) |
From these equations, the potential U can be estimated:
|
U = Q × d/(A × ε0 × εr) |
(17) |
For the nearly atomic distances, εr can be approximated for the vacuum (=1), and the expected double-layer thickness is in molecular dimensions (about 0.5 nm). Then, the change of nanoparticle potential UNP by one elementary charge qe can be approximated by:
|
UNP ≈ qe × 0.5 nm/(A × ε0) |
(18) |
Significant shifts in electrochemical potential should be expected for small nanoparticles, which means in the early stage of growth. In this phase, the reacting sites of the particle surface and their stochastic interactions with species from the solution have a large effect on the electrochemical state of a particle (Figure 2). It has to be kept in mind that changes of some tens of millivolts typically have a significant effect on the intensity of electrochemical processes, and changes of several hundred millivolts are related to strong changes in the electrochemical process intensities, often connected with drastic changes in the general chemical behavior. The estimation shows that such strong effects caused by fluctuations of single elementary charges must be expected for small particles with sizes below about 2 to 4 nm.
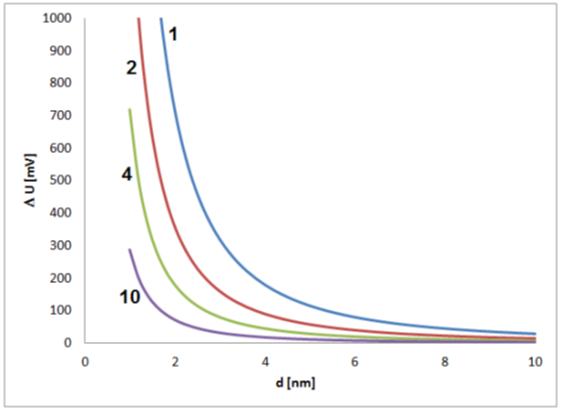 Figure 2. Estimated contribution of a single elementary charge on the potential of a single metal nanoparticle in dependence on the particle size for values of dielectric constant (electrical permittivity) of 1, 2, 4 and 10 and an assumed thickness of the electrochemical double layer of 0.5 nm.
Figure 2. Estimated contribution of a single elementary charge on the potential of a single metal nanoparticle in dependence on the particle size for values of dielectric constant (electrical permittivity) of 1, 2, 4 and 10 and an assumed thickness of the electrochemical double layer of 0.5 nm.
In a later phase, when the particle consists already of about thousands or more atoms, these stochastic effects are less important for the state of the particle, and its electrochemical potential is mainly controlled by the concentration of the electrochemically active components of the solution and the general particle surface state.
The particle potential remains nearly constant in the latest phase of particle growth if the particle is larger and the changes of concentrations of reacting components in the solution become negligible. In the case of constant electrochemical potential, the sum of all partial currents of electrochemical processes is zero. That means that the currents of all cathodic partial processes I are completely compensated by the electrochemical currents of anodic partial processes I+:
|
|I+| = |I−| |
(19) |
The electrochemical potential of a growing metal nanoparticle increases when the intensity of cathodic partial process (metal deposition) exceeds the intensity of the anodic partial process:
|
|I+ | < |I− | à increasing particle potential |
(20) |
The electrochemical potential of a growing metal nanoparticle decreases when the intensity of the anodic partial process (oxidation of reducing agent) exceeds the intensity of the cathodic partial process:
|
|I+| > |I−| à decreasing particle potential |
(21) |
4. Self-Polarization Effects of Nonspherical Metal Nanoparticles
Metal nanoparticles are marked by a high mobility of charges. This matches the electron gas model of metallic solids and is valid for charged nanoparticles (or ion-like clusters), too. The electrical excess charges of metal nanoparticles are fluctuating, but the fluctuation of single elementary charges is coupled with the others due to electrostatic repulsion. Therefore, the charges are concentrated at the surface of the particle. Spherical particles are marked by a regular distribution of the excess charges at their surface due to the tendency to maximize the distances between all single charges.
The symmetry in the charge distribution gets lost if the shape symmetry of a sphere is broken. The distribution of charges then depends on the particle shape and two or more charge centers of gravity appear. Some examples of such geometry-dependent charge distributions are shown in Figure 3.
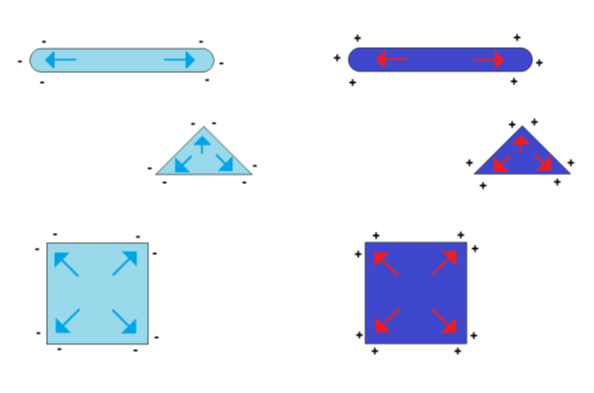 Figure 3. Formation of charge centers of gravity in the case of electrically charged nonspherical metal nanoparticles (blue symbolizing negative excess charge, red symbolizing positive excess charge)
Figure 3. Formation of charge centers of gravity in the case of electrically charged nonspherical metal nanoparticles (blue symbolizing negative excess charge, red symbolizing positive excess charge)
This effect of the self-polarization of charged nanoparticles is in strong contrast to the charge distribution of macroscopic metallic objects. Due to the smaller dimensions of the nanoparticles, its charge distribution is closer to the conditions in molecules with delocalized electrons than to the electrical conditions in a larger metal body, in which the charge distribution is dominated by thermal fluctuations for temperatures near room temperature. This effect can easily be illustrated by the comparison between the change of thermal energy ΔT and electrostatic energy for single elementary charges in dependence on charge distance r:
|
[1/(4επ)] × qe2/r = kB × ΔT |
(22) |
|
ΔT = [1/(4επ)] × qe2/(r × kB) |
(23) |
The strength of the effect depends on the relative permittivity εr. This is a dimensionless material-specific parameter that can be assumed to be in the range between about 5 and 100. For this range, significant self-polarization effects that are not leveled by thermal fluctuations should be expected for nonspherical particles between about a few tens and few hundreds of nanometers size depending on the material (Figure 4).
The self-polarization effect has important consequences for the growth and for the corrosion behavior of metal nanoparticles. The simplest case is the self-polarization of a nanorod, and this case can serve as an example to explain the principle effects. Dictated by the repulsion of equal charges, the charges are concentrated on the poles of the nanorod.
In the case of a positive excess charge, the potential is higher on the poles and lower in the center of the particle (Figure 5a). This means that in the case of corrosion, the poles are corroded faster than the center due to the higher intensity of the potential-dependent anodic partial on the pole. In the case of deposition (particle growth), a positive excess charge lowers the deposition on the poles and enhances the deposition in the center region. Thus, it is expected that at a positive excess charge, corrosion and deposition result in the lowering of the aspect ratio.
In the case of a negative excess charge, the potential at the poles is decreased stronger than in the center of a nanorod (Figure 5b). This means that the deposition rate is enhanced on the poles and lowered in the center. This promotes the growth in the axial direction or the forming of “dog bone”-like geometries. In the case of corrosion, the material loss is lowered on the poles but enhanced in the center leading to a thinning of the central region. Both processes result in the tendency of an increase in the aspect ratio or the bone-shaping of nanorods.
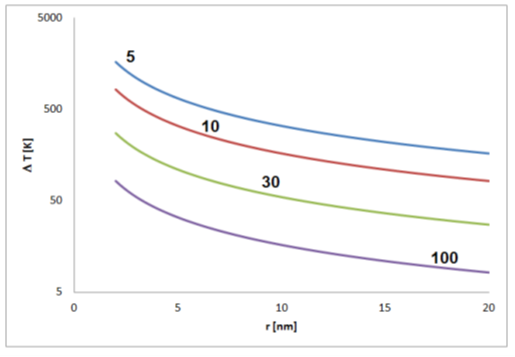 Figure 4. Estimated temperature differences T corresponding to the thermal energy equal to the electrostatic energy of a pair of elementary charges in distance r (for permittivity of 5, 10, 30 and 100).
Figure 4. Estimated temperature differences T corresponding to the thermal energy equal to the electrostatic energy of a pair of elementary charges in distance r (for permittivity of 5, 10, 30 and 100).
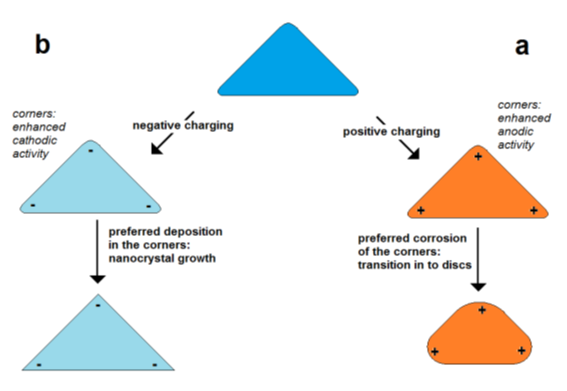 Figure 5. Self-polarization effect: effect of excess charge on the change of particle shape in dependence on charge sign shown for the example of a flat triangular metal nanoprism (schematically); (a) enhanced positive charge in the corners of triangular particle, (b) enhanced negative charge in the corners of particles
Figure 5. Self-polarization effect: effect of excess charge on the change of particle shape in dependence on charge sign shown for the example of a flat triangular metal nanoprism (schematically); (a) enhanced positive charge in the corners of triangular particle, (b) enhanced negative charge in the corners of particles
5. Factors in Shape Control of Growing Metal Nanoparticles
Some general mechanisms can be formulated for the evolution of metal nanoparticle shape during particle growth [25]. It has to be kept in mind that surface energy plays a crucial role in metal deposition and etching in addition to the electrochemical potential [26]. Therefore, the lattice structure of the growing or corroding nanorods and the crystallographic planes at the particle surface are further important factors for the resulting geometries. However, considering the above-mentioned size-dependent effects, it can be concluded that a stronger influence of the lattice structure on the geometry evolution in the case of larger particles can be expected, whereas small particles are probably strongly dependent on the electrochemical potentials and self-polarization effects. It is well known that halogen ions determine the character of metal nanoparticle growth by the formation of adsorbates [27,28]. In addition, surfactants and their specific interaction with crystal planes are important for the shape development of metal nanoparticles [29,30]. In the case of the specific adsorption of shape-steering additives on preferred lattice planes and their inhibition of local metal deposition during the nanoparticle formation, it can be assumed that electrochemical effects such as self-polarization modulate the anisotropic particle growth and shaping.
The formation of regular crystals can be expected if the adsorbing metal ions or the formed metal adatoms have a high surface mobility. In this case, they tend to move to a thermodynamically preferred place. The formation of regular crystal lattices is then controlled by the minimization of lattice energy.
In the case of lower surface mobility, there is a mixture between a random adsorption of metal ions and adatoms and energy-controlled translocation taking place. This can result in more or less regular crystal structures. A typical result is the formation of branched crystals and dendritic nanocrystals with local crystallinity and a combination of different lattice orientations in different domains of the nanoparticle. In addition to the random adsorption of metal ions, an accidental local binding of ligands or other molecular effectors can influence the growth behavior of nanoparticles and also the formation of branched or polycrystalline structures.
Random effects in the attachment of adsorbing metal ions on the nanoparticle surface and the tendency of binding on thermodynamically excellent sites are superposed by the electrostatic self-polarization effect. On the one hand, local electrical fields direct approaching ionic species into preferred regions of the growing particle. On the other hand, the distribution of electrical charges on the particle surface modulates the local surface energy. The formation of different aspect ratios or the appearance of dog-bone-like nanorod structures is a typical consequence of this effect.
In addition to the shape control, the size control in the formation of metal nanoparticles is also very important because the electronic and optical properties of metal nanoparticles are size dependent. For the growth of larger nanoparticles from seed particles, the ratio of seed concentration to the concentration of precursor is generally the key parameter for steering the particle size. In the case of the complete consumption of the precursor during a homogeneous nanoparticle growth, this ratio determines the particle size directly. High seed concentrations result in small final product particles, and low seed concentrations cause the formation of large particles.
6. Electrically Controlled Assembly of Metal Nanoparticles
The use of attractive forces of oppositely charged nanoparticles is a simple strategy for their assembly. However, the mixing of particles of opposite charges involves the possibility of fast coagulation. A particle of one type can act as “particle glue” for connecting the particles of another type. Therefore, it is important to work with suitable particle concentrations (Figure 6).
Assembly can also take place in the case of equally charged particles. Therefore, forces are needed for overcoming the barrier of electrostatic repulsion. The electrostatic repulsion of charged nanoparticles is well known for the stabilization of the colloidal state. The domination of kinetic energy and binding over repulsion leads to the aggregation of particles, which can finally result in complete coagulation and precipitation. In other cases, moderate lowering of the particle velocity while maintaining the particle charges can cause the limited assembly and restabilization of colloids. Such a mechanism can cause the formation of polycrystalline metal nanoparticles by an in situ assembly process during Au nanoparticle formation, as discovered by Polte et al. [24], and is also a probable reason for the formation of star-like Au/Ag nanoparticles [31].
Discharging of colloidal particles can be induced by:
- Raising the general ion concentrations, which means the ionic strength (“salt-out effect”);
- Targeted addition of antagonistic ions, which means metal cations with high surface affinity in the case of negatively charged particles;
- Targeted addition of surface-affine anions or electron-donor ligands in the case of positively charged particles;
- Lowering the electrochemical potential of particles in the case of positively charged particles by enhancing the concentration of reducing agents;
- Raising the electrochemical potential in the case of negatively charged particles by the addition of oxidizing agents.
In all cases, a restabilization mechanism has to take place in order to avoid a continuation of aggregation, the uncontrolled formation of large aggregates and precipitation. In principle, this restabilization can be induced by controlling the electrochemical particle potential, too. Therefore, a “backward strategy” or a “forward strategy” can be applied. In the “backward strategy”, the addition of complementary effectors invert the primary-induced potential shift for the stabilization of colloids after the temporary destabilization. The idea behind the “forward strategy” is to continue the primary-induced potential shift in the same direction to overcome the zero-potential point quickly and to achieve the colloidal restabilization by inversion of the charge sign. Thus, the addition of adsorbing anions or the stepwise enhancement of the reducing agent concentration can lower the positive potential of colloidal metal nanoparticles in a first step but can lead to restabilized colloids by negatively charged particles. On the other hand, a colloid of negatively charged metal nanoparticles can be destabilized by the addition of oxidizing agents or metal cations but restabilized by their further addition in the positive potential range. It has to be mentioned that the addition of oxidizing agents has to be performed carefully in order to avoid the corrosion or complete dissolution of the colloidal particles. It seems that reductants can also cause a disruption of particles, especially strong ones such as NaBH4, by inducing a Rayleigh instability [32].
Self-polarization or the induced polarization of nonspherical particles causes different conditions for particle–particle interactions dependent on position. This can decide the formation of compact, linear or branched assemblies. Such different behavior was observed on polarizable polymer nanoparticles carrying polyionic macromolecules [33], and it can be, obviously, the reason for the formation of linear branched and network structures in the in situ assembly of metal nanoparticles.
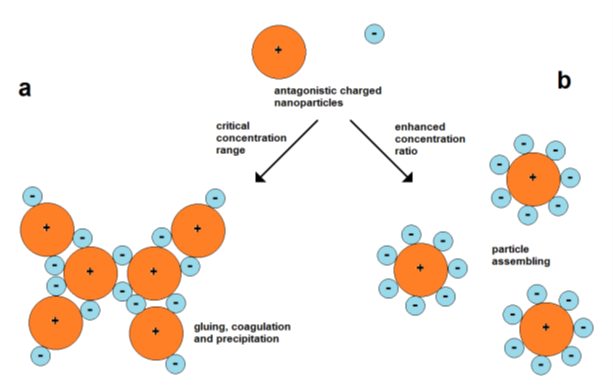 Figure 6. Coagulation and assembly of oppositely charged nanoparticles; (a) high probability of coagulation at lower concentration ratios, (b) forming of dispersed assemblies at higher concentration ratios between small negative and larger positive particles
Figure 6. Coagulation and assembly of oppositely charged nanoparticles; (a) high probability of coagulation at lower concentration ratios, (b) forming of dispersed assemblies at higher concentration ratios between small negative and larger positive particles
7. Secondary Metal Deposition
An electrostatic model was proposed for the formation of networks of Au/Ag nanoparticles during the deposition of silver on preformed spherical gold nanoparticles [34]. It describes the preferred bonding of spherical particles on the poles of nanorods due to the induced polarization by the electrostatic interaction of the charged metal nanoparticles. This preferred bonding on the poles leads to the successive prolongation of primary formed nonspherical aggregates. The intrinsic reason for this linear aggregation is the symmetry break by binding of two spherical nanoparticles, which means a transition from a spherical geometry into a body with an enhanced aspect ratio. This initial process is responsible for the symmetry break in the distribution of surface charges. High repulsion forces result in a strict linear growth. Lower charging means a certain probability of occasional binding events on intermediate positions, working as branching points.
In general, higher electrical charges lead to more stable colloids and a separate growth of single nanoparticles, whereas lower electrical charges enhance the tendency of aggregation. The aggregation can end with restabilization after a few binding events after the formation of larger aggregates or networks or lead to complete coagulation and precipitation [35]. These effects can well be observed in the deposition of silver on preformed gold nanoseeds. In the case of a strong dominance of positively charged silver cations, the colloid remains stable at a higher potential. In the case of a reduced charge, particles can join each other. Due to the mobility of electrical charges, self-polarization takes place, and a preferred axial growth results in rod- and astragal-like structures (Figure 7). Therefore, not only are compact aggregates observed but also single particles. Further in situ aggregation during silver deposition can lead to branched astragal-like structures and to the formation of nanoparticle networks (examples in Figure 8).
The effect of electrical control and self-polarization is well reflected by the formation of nanoframe structures by galvanic replacement reactions [36,37]. The deposition of gold on flat silver nanotriangles starts on the edges, at the preferred cathodically active sites, whereas the corrosion of silver starts in the center of the particles, at the preferred anodically active area. As a result, a central hole is formed, and the original prismatic particle shape is transformed into a frame structure (Figure 9).
The interplay between lattice-directed metal deposition and accidental deposition can be nicely observed in the case of the formation of Au/Pt nanorods [38]. The seed-like gold nanorods are positively charged due to adsorbed cetyltrimethylammonium cations (CTAB). This charge and, therefore, the electrochemical potential of the nanoparticles, are lowered by the addition of the reducing agent, which can be oxidized on the particle surface. If a slight reduction of potential only occurs, the nucleation of platinum can only proceed on crystallographic exposed points on the gold surface. As a result, the structure of the deposited platinum nanocrystallites follows the borderlines between the crystallographic surface planes of gold nanorods. At low deposition rates, the nucleation of platinum starts on these borderlines between the crystallographic planes of the single-crystalline gold nanorods. The decoration of these crystallographic lines by the platinum crystallites is clearly visible in the SEM images (Figure 10a). At moderately enhanced platinum deposition activities (enhanced platinum precursor concentration), the nucleation of platinum also takes place on the crystallographic planes; the decoration effect of the borderlines between the planes, however, remains visible (Figure 10b). In this case, a more stochastic distribution of platinum crystallites in the shell is formed. At a higher precursor concentration, the nucleation probability generally increases, the dominance of the borderline-directed nucleation disappears, and a comparatively dense shell of platinum crystallites is formed around the gold core (Figure 10c).
 Figure 7. Assembly behavior of charged metal nanoparticles: (a) spherical nanoparticles; (b) nonspherical metal nanoparticles, for example nanodiscs.
Figure 7. Assembly behavior of charged metal nanoparticles: (a) spherical nanoparticles; (b) nonspherical metal nanoparticles, for example nanodiscs.
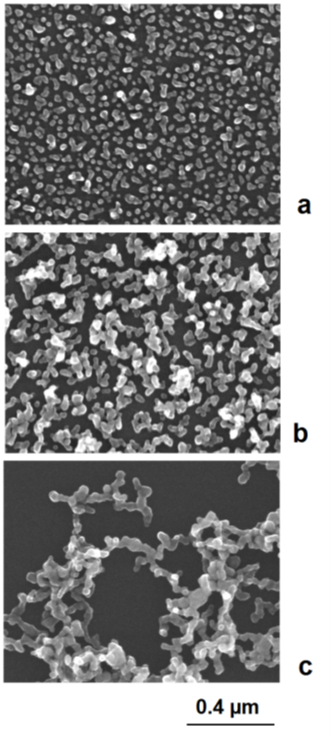 Figure 8. In situ formation of aggregate particles during the chemical deposition of silver nanoparticles on gold seeds: (a) small aggregate particles; (b) enhanced aggregate size; (c) network formation.
Figure 8. In situ formation of aggregate particles during the chemical deposition of silver nanoparticles on gold seeds: (a) small aggregate particles; (b) enhanced aggregate size; (c) network formation.
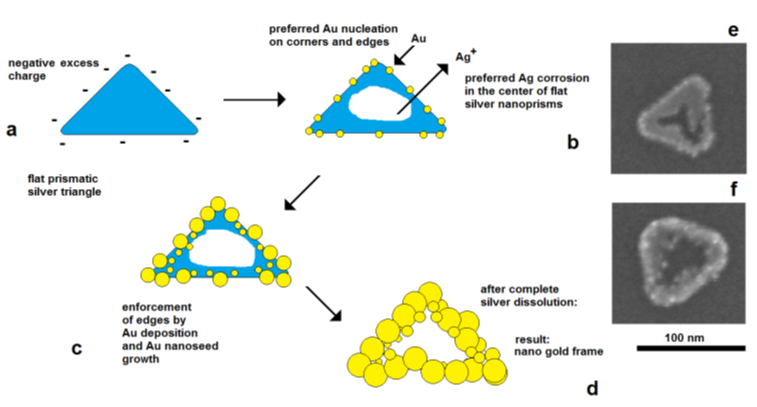 Figure 9. Electrically controlled formation of metal frame particles by the substitution of a less-noble metal by a noble metal. Deposition of gold on flat silver nanotriangles: (a) negatively charged silver nanotriangles in the colloidal state; (b) starting gold deposition on the particle edges (lowest potential) and starting silver corrosion in the center of the flat prism (highest potential); (c) enforcement of gold in the edge regions of particles; (d) formation of a gold frame by the complete dissolution of silver (schematically); (e) silver triangle with a hole formation in the particle center; (f) advanced silver dissolution and edge-directed gold deposition (SEM images).
Figure 9. Electrically controlled formation of metal frame particles by the substitution of a less-noble metal by a noble metal. Deposition of gold on flat silver nanotriangles: (a) negatively charged silver nanotriangles in the colloidal state; (b) starting gold deposition on the particle edges (lowest potential) and starting silver corrosion in the center of the flat prism (highest potential); (c) enforcement of gold in the edge regions of particles; (d) formation of a gold frame by the complete dissolution of silver (schematically); (e) silver triangle with a hole formation in the particle center; (f) advanced silver dissolution and edge-directed gold deposition (SEM images).
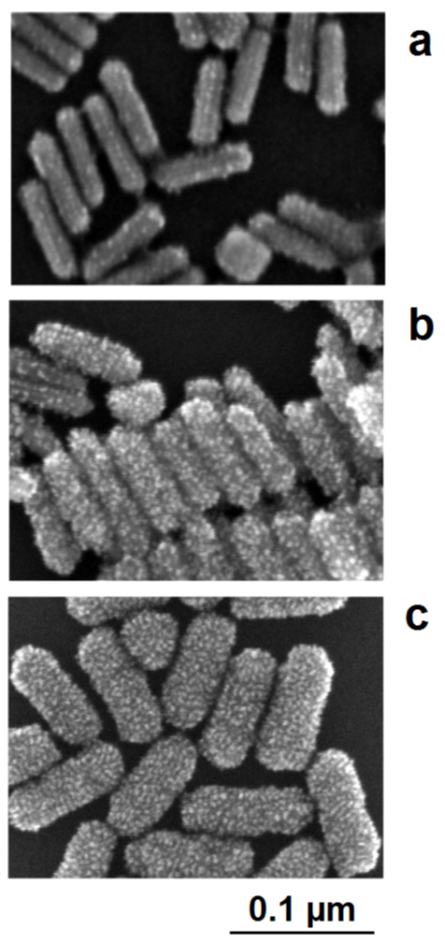 Figure 10. Interplay between the lattice-controlled and accidental nucleation of platinum on gold nanorods: (a) lowest platinum precursor concentration: decoration of borderlines between crystallographic planes; (b) mediate precursor concentration: additional nucleation on the crystallographic planes between the excellent borderlines; (c) high platinum precursor concentration: densified platinum deposition as a shell around the gold core.
Figure 10. Interplay between the lattice-controlled and accidental nucleation of platinum on gold nanorods: (a) lowest platinum precursor concentration: decoration of borderlines between crystallographic planes; (b) mediate precursor concentration: additional nucleation on the crystallographic planes between the excellent borderlines; (c) high platinum precursor concentration: densified platinum deposition as a shell around the gold core.
8. Conclusions
Metal nanoparticles in colloidal solutions are electrically charged and electrochemically active objects. The electrochemical point of view allows for an understanding of many phenomena related to the growth, formation and interaction of metal nanoparticles in colloidal solution. It illustrates the analogy between macroscopic electrochemical open-circuit and mixed-electrode systems and metal nanoparticles in the colloidal state. However, this point of view also reflects the specificities of electrochemical processes that are related to the small, meaning nearly molecular, size of the electrode-like nano-objects, the role of small numbers of elementary charges, self-polarization effects of nonspherical nanoparticles and the interplay between lattice-dominated, potential-dominated and accidental elementary events. The electrochemical point of view is well suited for understanding the stabilization, destabilization and restabilization of spherical nanoparticles in colloidal solution, as well as the growth characteristics of nonspherical metal nanoparticles, the formation of binary nanoparticles and particle/particle interaction. The combination of electrochemical activity and self-polarization of charged metallic nano-objects also gives a conclusive explanation of the aggregation behavior of nanoparticles in colloidal solution and for the formation of linear, branched and network-like structures.
