Multivariate analysis (MA) is becoming a fundamental tool for processing in an efficient way the large amount of data collected in X-ray diffraction experiments. Multi-wedge data collections can increase the data quality in case of tiny protein crystals; in situ or operando setups allow investi-gating changes on powder samples occurring during repeated fast measurements; pump and probe experiments at X-ray free-electron laser (XFEL) sources supply structural characterization of fast photo-excitation processes. In all these cases, MA can facilitate the extraction of relevant in-formation hidden in data, disclosing the possibility of automatic data processing even in absence of a priori structural knowledge.
- multivariate analysis
- chemometrics
- principal com
1. Introduction
Multivariate analysis (MA) consists of the application of a set of mathematical tools to problems involving more than one variable in large datasets, often combining data from different sources to find hidden structures. MA provides decomposition in simpler components and makes predictions based on models or recovers signals buried in data noise.
Analysis of dependency of data in more dimensions (or variables) can be derived from the former work of Gauss on linear regression (LR) and successively generalized to more than one predictor by Yule and Pearson, who reformulated the linear relation between explanatory and response variables in a joint context [1][2].
The need to solve problems of data decomposition into simpler components and simplify the multivariate regression using few, representative explanatory variables brought towards the advent of the principal component analysis (PCA) by Pearson and, later, by Hotelling [3][4] in the first years of the 20th century. Since then, PCA has been considered a great step towards data analysis exploration because the idea of data decomposition into its principal axes (analogies with mechanics and physics were noted by the authors) allows the data to be explained into a new multidimensional space, where directions are orthogonal to each other (i.e., the new variables are uncorrelated) and each successive direction is decreasing in importance and, therefore, in explained variance. This paved the way to the concept of dimensionality reduction [5] that is crucially important in many research areas such as chemometrics.
Chemometrics involves primarily the use of statistical tools in analytical chemistry [6] and, for this reason, it is as aged as MA. It is also for this reason that the two disciplines started to talk since the late 1960s, initially concerning the use of factor analysis (FA) in chromatography [7]. FA is a different way to see the same problem faced by PCA, as in FA data are explained by hidden variables (latent variables or factors) by using different conditions for factor extraction [8], while in PCA components are extracted by using the variance maximization as unique criterion. Since then, chemometrics and MA have contaminated each other drawing both advantages [9].
Multivariate curve resolution (MCR) [10] is a recent development consisting in the separation of multicomponent systems and able to provide a scientifically meaningful bilinear model of pure contributions from the information of the mixed measurements. Another data modeling tool is the partial least square (PLS) [11], a regression method that avoids the bad conditioning intrinsic of LR by projecting the explanatory variables onto a new space where the variables are uncorrelated each other, but maximally correlated with the dependent variable. PLS has been successfully applied in problems such as quantitative structure-activity vs. quantitative structure-property of dataset of peptides [12] or in the analysis of relation of crystallite shapes in synthesis of super-structures of CaCO3 through a hydrogel membrane platform [13].
Moreover, classification methods have been adopted in chemometrics since the beginning, mainly for pattern recognition, i.e., classification of objects in groups according to structures dictated by variables. Discriminant analysis (DA), PLS-DA [14], support vector machines (SM) [15] have been used for problems such as classification of food quality or adulteration on the basis of sensitive crystallization [16], toxicity of sediment samples [17] or in classification of biomarkers [18], gene data expression or proteomics [19] just to mention few examples.
MA has been also used to improve the signal-to-noise ratio in measurements. Methods such as phase sensitive detection (PSD) have been developed and implemented for technical applications as in the lock-in amplifier, which amplifies only signals in phase with an internal reference signal. PSD has found a large applications in chemometrics connected to excitation enhanced spectroscopy, where it has been used to highlight excitation-response correlations in chemical systems [20]. Summarizing, although widely used in analytical chemistry, MA is less diffused in materials science and certainly under-exploited in crystallography, where much wider applications are forecast in the next decade.
2. Multivariate Methods
2.1. High Dimension and Overfitting
MA provides answers for prediction, data structure, parameter estimations. In facing these problems, we can think at data collected from experiments as objects of an unknown manifold in a hyperspace of many dimensions [21]. In the context of X-ray diffraction, experimental data are constituted by diffraction patterns in case of single crystals or diffraction profiles in case of powder samples. Diffraction patterns, after indexing, are constituted by a set of reflections, each identified by three integers (the Miller indices) and an intensity value, while diffraction profiles are formed by 2ϑ values as independent variable and intensity values as dependent variable. The data dimensionality depends on the number of reflections or on the number of 2ϑ values included in the dataset. Thus, high-resolution data contain more information about the crystal system under investigation, but have also higher dimensionality.
In this powerful and suggestive representation, prediction, parameter estimation, finding latent variables or structure in data (such as classify or clustering) are all different aspects of the same problem: model the data, i.e., retrieve the characteristics of such a complex hypersurface plunged within a hyperspace, by using just a sampling of it. Sometimes, few other properties can be added to aid the construction of the model, such as the smoothness of the manifold (the hypersurface) that represents the physical model underlying the data. Mathematically speaking, this means that the hypersurface is locally homeomorphic to a Euclidean space and can be useful to make derivatives, finding local minimum in optimization and so on.
In MA, it is common to consider balanced a problem in which the number of variables involved is significantly fewer than the number of samples. In such situations, the sampling of the manifold is adequate and statistical methods to infer its model are robust enough to make predictions, structuring and so on. Unfortunately, in chemometrics it is common to face problems in which the number of dimensions is much higher than the number of samples. Some notable examples involve diffraction/scattering profiles, but other cases can be found in bioinformatics, in study for gene expression in DNA microarray [22][23]. Getting high resolution data is considered a good result in Crystallography. However, this implies a larger number of variables describing a dataset: (more reflections in case of single-crystal data or higher 2ϑ values in case of powder data). Consequently, it makes more complicated the application of MA.
When the dimensionality increases, the volume of the space increases so fast that the available data become sparse on the hypersurface, making it difficult to infer any trend in data. In other words, the sparsity becomes rapidly problematic for any method that requires statistical significance. In principle, to keep the same amount of information (i.e., to support the results) the number of samples should grow exponentially with the dimension of the problem.
A drawback of having a so much high number of dimensions is the risk of overfitting. Overfitting is an excessive adjustment of the model to data. When a model is built, it must account for an adequate number of parameters in order to explain the data. However, this should not be done too precisely, so to keep the right amount of generality in explaining another set of data that would be extracted from the same experiment or population. This feature is commonly known as model’s robustness. Adapting a model to the data too tightly introduces spurious parameters that explain the residuals and natural oscillations of data commonly imputed to noise. This known problem was named by Bellman the “curse of dimensionality”, but it has other names (e.g., the Hughes phenomenon in classification). A way to partially mitigate such impairment is to reduce the number of dimensions of the problem, giving up to some characteristic of the data structure.
The dimensionality reduction can be performed by following two different strategies: selection of variables or transformation of variables. In the literature, the methods are known as feature selection and feature extraction [24].
Formally, if we model each variate of the problem as a random variable Xi, the selection of variables is the process of selecting a subset of relevant variables to be used for model construction. This selection requires some optimality criterion, i.e., it is performed according to an agreed method of judgement. Problems to which feature selection methods can be applied are the ones where one of the variables, Y, has the role of ‘response’, i.e., it has some degree of dependency from the remaining variables. The optimality criterion is then based on the maximization of a performance figure, achieved by combining a subset of variables and the response. In this way, each variable is judged by its level of relevance or redundancy compared to the others, to explain Y. An example of such a figure of performance is the information gain (IG) [25], which resorts from the concept of entropy, developed in the information theory. IG is a measure of the gain in information achieved by the response variable (Y) when a new variable (Xi) is introduced into the measure. Formally:
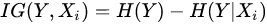 |
(1) |
being H() the entropy of the random variable. High value of IG means that the second term is little compared to the first one, , i.e., that when the new variable is introduced, it explains well the response and the corresponding entropy becomes low. The highest values of IG are used to decide which variables are relevant for the response prediction. If the response variable is discrete (i.e., used to classify), another successful method is Relief [26], which is based on the idea that the ranking of features can be decided on the basis of weights coming from the measured distance of each sample (of a given class) from nearby samples of different classes and the distance of the same sample measured from nearby samples of the same class. The highest weights provide the most relevant features, able to make the best prediction of the response.
Such methods have found application in the analysis of DNA microarray data, where the number of variables (up to tenths of thousands) is much higher than the number of samples (few hundreds), to select the genes responsible for the expression of some relevant characteristic, as in the presence of a genetic disease [27]. Another relevant application can be found in proteomics [28], where the number of different proteins under study or retrieved in a particular experimental environment is not comparable with the bigger number of protein features, so that reduction of data through the identification of the relevant feature becomes essential to discern the most important ones [29].
Feature extraction methods, instead, are based on the idea of transforming the variables set into another set of reduced size. Using a simple and general mathematical formulation, we have:
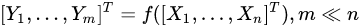 |
(2) |
with the output set [Y1,…,Ym] a completely different set of features from the input [X1,…,Xn], but achieved from them. Common feature-extraction methods are based on linear transformation, i.e.,
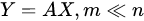 |
(3) |
where the variables are transformed losing their original meaning to get new characteristics that may reveal some hidden structure in data.
Among these methods, PCA is based on the transformation in a space where variables are all uncorrelated each other and sorted by decreasing variance. Independent Component Analysis (ICA), instead, transforms variables in a space where they are all independent each other and maximally not-Gaussian, apart for one, which represents the unexplained part of the model, typically noise. Other methods, such as MCR, solve the problem by applying more complicated conditions such as the positivity of the values in the new set of variables or similar, so that the physical meaning of the data is still preserved. A critical review of dimensionality reduction feature extraction methods is in Section 2.2.
PCA and MCR have an important application in solving mixing problems or in decomposing powder diffraction profiles of mixtures in pure-phase components. In such decomposition, the first principal components (or contributions, in MCR terminology) usually include the pure-phase profiles or have a high correlation with these.
2.2. Dimensionality Reduction Methods
In Section 2.1, the importance of applying dimensionality reduction to simplify the problem view and reveal underlying model within data was underlined. One of the most common method to make dimensionality reduction is principal component analysis.
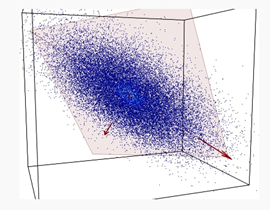
PCA is a method to decompose a data matrix finding new variables orthogonal each other (i.e., uncorrelated), while preserving the maximum variance (see Figure 1). These new uncorrelated variables are named principal components (PCs).
Figure 1. A set of data (blue dots) of three variables is represented into a 3D space. Data are mostly spread on the orange plane, with little departure from it. Principle component analysis (PCA) identifies the plane and the directions of maximum variability of data within it.
PCA is then an orthogonal linear transformation that transforms data from the current space of variables to a new space of the same dimension (in this sense, no reduction of dimension is applied), but so that the greatest variance lies on the first coordinate, the second greatest variance on the second coordinate and so on. From a mathematical viewpoint, said X the dataset, of size N × P (N being the number of samples, P that of the variates), PCA decomposes it so that
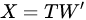 |
(4) |
with (of size N × P) the matrix of the principal components (called also scores), which are the transformed variable values corresponding to each sample and with (of size P × P) the matrix of the loadings, corresponding to the weights by which each original variable must be multiplied to get the component scores. The matrix is composed by orthogonal columns that are the eigenvectors of the diagonalization [30] of the sample covariance matrix of :
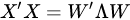 |
(5) |
In Equation (5), is a diagonal matrix containing the eigenvalues of the sample covariance matrix of , i.e., . Since a covariance matrix is always semi-definite positive, the eigenvalues are all real and positive or null and correspond to the explained variance of each principal component. The main idea behind PCA is that in making such decomposition, often occurs that not all the directions are equally important. Rather, the number of directions preserving most of the explained variance (i.e., energy) of the data are few, often the first 1–3 principal components (PC). Dimensionality reduction is then a lossy process, in which data are reconstructed by an acceptable approximation that uses just the first few principal components, while the remaining are neglected:
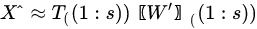 |
(6) |
With the retained components (i.e., the first s columns of both the matrices) and .
Diagonalization of the covariance matrix of data is the heart of PCA and it is achieved by resorting to singular value decomposition (SVD), a basic methodology in linear algebra. SVD should not be confused with PCA, the main difference being the meaning given to the results. In SVD the input matrix is decomposed into the product a left matrix of eigenvectors , a diagonal matrix of eigenvalues and a right matrix of eigenvectors , reading the decomposition from left to right:
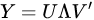 |
(7) |
SVD may provide decomposition also of rectangular matrices. PCA, instead, uses SVD for diagonalization of the data covariance matrix , which is square and semi-definite positive. Therefore, left and right eigenvector matrices are the same, and the diagonal matrix is square and with real and positive value included. The choice of the most important eigenvalues allows the choice of the components to retain, a step that is missing from SVD meaning.
Factor analysis is a method based on the same concept of PCA: a dataset is explained by a linear combination of hidden factors, which are uncorrelated each other, apart for a residual error:
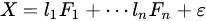 |
(8) |
FA is a more elaborated version of PCA in which factors are supposed (usually) to be known in number and, although orthogonal each other (as in PCA), they can be achieved adopting external conditions to the problem. A common way to extract factors in FA is by using a depletion method in which the dataset is subjected to an iterative extraction of factors that can be analyzed time by time: . In FA, there is the clear intent to find physical causes of the model in the linear combination. For this reason, their number is fixed and independency of the factors with the residual is imposed too. It can be considered, then, a supervised deconvolution of original dataset in which independent and fixed number of factors must be found. PCA, instead, explores uncorrelated directions without any intent of fixing the number of the most important ones.
FA has been applied as an alternative to PCA in reducing the number of parameters and various structural descriptors for different molecules in chromatographic datasets [31]. Moreover, developments of the original concepts have been achieved by introducing a certain degree of complexity such as the shifting of factors [32] (factors can have a certain degree of misalignment in the time direction, such as in the time profile for X-ray powder diffraction data) or the shifting and warping (i.e., a time stretching) [33].
Exploring more complete linear decomposition methods, MCR has found some success as a family of methods that solve the mixture analysis problem, i.e., the problem of finding the pure-phase contribution and the amount of mixing into a data matrix including only the mixed measurements. A typical paradigm for MCR, as well as for PCA, is represented by spectroscopic or X-ray diffraction data. In this context, each row of the data matrix represents a different profile, where the columns are the spectral channels or diffraction/scattering angles, and the different rows are the different spectra or profiles recorded during the change of an external condition during time.
In MCR analysis, the dataset is described as the contribution coming from reference components (or profiles), weighted by coefficients that vary their action through time:
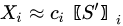 |
(9) |
With the vector of weights (the profile of change of the i-th profile through time) and the pure-phase i-th reference profile. The approximation sign is since MCR leaves some degree of uncertainty in the model. In a compact form we have:
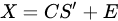 |
(10) |
MCR shares the same mathematical model of PCA, apart for the inclusion of a residual contribution that represents the part of the model we give up explaining. The algorithm that solves the mixture problem in the MCR approach, however, is quite different from the one used in PCA. While PCA is mainly based on the singular value decomposition (i.e., basically the diagonalization of its sample covariance matrix), MCR is based on the alternating least square (ALS) algorithm, an iterative method that tries to solve conditioned minimum square problems of the form:
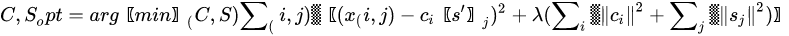 |
(11) |
The previous problem is a least square problem with a regularization term properly weighted by a Lagrange parameter . The regularization term, quite common in optimization problems, is used to drive the solution so that it owns some characteristics. The -norm of the columns of or , as reported in the Equation (11), is used to minimize the energy of the residual and it is the most common way to solve ALS. However, other regularizations exist, such as -norm to get more sparse solutions [34] or imposing positivity of the elements of and . Usually, the solution to Equation (11) is provided by iterative methods, where initial guesses of the decomposition matrices or are substituted iteratively by alternating the solution of the least-square problem and the application of the constraints. In MCR, the condition of positivity of elements in both or is fundamental to give physical meaning to matrices that represent profile intensity and mixing amounts, respectively.
The MCR solution does not provide the direction of maximum variability as PCA. PCA makes no assumption on data; the principal components and particularly the first one, try to catch the main trend of variability through time (or samples). MCR imposes external conditions (such as the positivity), it is more powerful, but also more computationally intensive. Moreover, for quite complicated data structures, such as the ones modeling the evolution of crystalline phases through time [35][36], it could be quite difficult to impose constraints into the regularization term, making the iterative search unstable if not properly set [37][38]. Another important difference between MCR and PCA is in the model selection: in MCR the number of latent variables (i.e., the number of profiles in which decomposition must be done) must be known and set in advance; in PCA, instead, while there are some criterion of selection of the number of significative PC such as the Malinowski indicator function (MIF) [39][40] or the average eigenvalue criterion (AEC) [41][42], it can also be inferred by simply looking at the trend of the eigenvalues, which is typical of an unsupervised approach. The most informative principal components are the ones with highest values.
For simple mathematical models, it will be shown in practical cases taken from X-ray diffraction that PCA is able to optimally identify the components without external constraints. In other cases, when the model is more complicated, we successfully experimented a variation of PCA called orthogonal constrained component rotation (OCCR) [43]. In OCCR, a post-processing is applied after PCA aimed at revealing the directions of the first few principal components that can satisfy external constraints, given by the model. The components, this way, are no longer required to keep the orthogonality. OCCR is then an optimization method in which the selected principal components of the model are let free to explore their subspace until a condition imposed by the data model is optimized. OCCR has been shown to give results that are better than traditional PCA, even when PCA produces already satisfactory results. A practical example (see Section 3) is the decomposition of the MED dataset in pure-phase profiles, where PCA scores, proportional to profiles, may be related each other with specific equations.
Smoothed principal component analysis or (SPCA) is a modification of common PCA suited for complex data matrices coming from single or multi-technique approaches where the time is a variable, in which sampling is a continuous, such as in situ experiment or kinetic studies. The ratio behind the algorithm proposed by Silvermann [44] is that data without noise should be smooth. For this reason, in continuous data, such as profiles or time-resolved data, the eigenvector that describes the variance of data should be also smooth [45]. Within these assumptions, a function called “roughness function” is inserted within the PCA algorithm for searching the eigenvectors along the directions of maximum variance. The aim of the procedure is reducing the noise in the data by promoting the smoothness between the eigenvectors and discouraging more discrete and less continuous data. SPCA had been successfully applied to crystallographic data in solution-mediated kinetic studies of polymorphs, such as L-glutamic acid from α to β form by Dharmayat et al. [46] or p-Aminobenzoic acid from α to β form by Turner and colleagues [47].
This entry is adapted from the peer-reviewed paper 10.3390/cryst11010012
References
- Pearson, K.; Yule, G.U.; Blanchard, N.; Lee, A. The Law of Ancestral Heredity. Biometrika 1903, 2, 211–236.
- Yule, G.U. On the Theory of Correlation. J. R. Stat. Soc. 1897, 60, 812–854.
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417.
- Jolliffe, I.T. Principal Components Analysis, 2nd ed.; Springer: Berlin, Germany, 2002.
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957.
- Brereton, R.G. The evolution of chemometrics. Anal. Methods 2013, 5, 3785–3789.
- Massart, D.L. The use of information theory for evaluating the quality of thin-layer chromatographic separations. J. Chroma-togr. A 1973, 79, 157–163.
- Child, D. The Essentials of Factor Analysis, 3rd ed.; Bloomsbury Academic Press: London, UK, 2006.
- Bro, R.; Smilde, A.K. Principal Component Analysis. Anal. Methods 2014, 6, 2812–2831.
- De Juan, A.; Jaumot, J.; Tauler, R. Multivariate Curve Resolution (MCR). Solving the mixture analysis problem. Anal. Methods 2014, 6, 4964–4976.
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130.
- Hellberg, S.; Sjöström, M.; Wold, S. The prediction of bradykinin potentiating potency of pentapeptides, an example of a pep-tide quantitative structure–activity relationship. Acta Chem. Scand. B 1986, 40, 135–140.
- Di Profio, G.; Salehi, S.M.; Caliandro, R.; Guccione, P. Bioinspired Synthesis of CaCO3 Superstructures through a Novel Hy-drogel Composite Membranes Mineralization Platform: A Comprehensive View. Adv. Mater. 2015, 28, 610–616.
- Ballabio, D.; Consonni, V. Classification tools in chemistry: Part 1: Linear models. PLS-DA. Anal. Methods 2013, 5, 3790–3798.
- Xu, Y.; Zomer, S.; Brereton, R. Support vector machines: A recent method for classification in chemometrics. Crit. Rev. Anal. Chem. 2006, 36, 177–188.
- Ellis, D.L.; Brewster, V.L.; Dunn, W.B.; Allwood, J.W.; Golovanov, A.P.; Goodacrea, R. Fingerprinting food: Current technol-ogies for the detection of food adulteration and contamination. Chem. Soc. Rev. 2012, 41, 5706–5727.
- Alvarez-Guerra, M.; Ballabio, D.; Amigo, J.M.; Viguri, J.R.; Bro, R. A chemometric approach to the environmental problem of predicting toxicity in contaminated sediments. J. Chemom. 2009, 24, 379–386.
- Heinemann, J.; Mazurie, A.; Lukaszewska, M.T.; Beilman, G.L.; Bothner, B. Application of support vector machines to metabolomics experiments with limited replicates. Metabolomics 2014, 10, 1121–1128.
- Huang, S.; Cai, N.; Pacheco, P.P.; Narandes, S.; Wang, Y.; Xu, W. Applications of SVM Learning Cancer Genomics. Cancer Genom. Proteom. 2018, 15, 41–51.
- Schwaighofer, A.; Ferfuson-Miller, S.; Naumann, R.L.; Knoll, W.; Nowak, C. Phase-sensitive detection in modulation excita-tion spectroscopy applied to potential induced electron transfer in crytochrome c oxidase. Appl. Spectrosc. 2014, 68, 5–13.
- Izenmann, A.J. Introduction to Manifold Learning. Wires Comput. Stat. 2012, 4, 439–446.
- Jaumot, J.; Tauler, R.; Gargallo, R. Exploratory data analysis of DNA microarrays by multivariate curve resolution. Anal. Bio-chem. 2006, 358, 76–89.
- Culhane, A.C.; Thioulouse, J.; Perrière, G.; Higgins, D.G. MADE4: An R package for multivariate analysis of gene expression data. Bioinformatics 2005, 21, 2789–2790.
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning, 8th ed.; Casella, G., Fienberg, S., Olkin, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; p. 204.
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106.
- Kira, K.; Rendell, L. A Practical Approach to Feature Selection. In Proceedings of the Ninth International Workshop on Ma-chine Learning, Aberdeen, UK, 1–3 July 1992; pp. 249–256.
- Kumar, A.P.; Valsala, P. Feature Selection for high Dimensional DNA Microarray data using hybrid approaches. Bioinfor-mation 2013, 9, 824–828.
- Giannopoulou, E.G.; Garbis, S.D.; Vlahou, A.; Kossida, S.; Lepouras, G.; Manolakos, E.S. Proteomic feature maps: A new visualization approach in proteomics analysis. J. Biomed. Inform. 2009, 42, 644–653.
- Lualdi, M.; Fasano, M. Statistical analysis of proteomics data: A review on feature selection. J. Proteom. 2019, 198, 18–26.
- Anton, H.; Rorres, C. Elementary Linear Algebra (Applications Version), 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2000.
- Stasiak, J.; Koba, M.; Gackowski, M.; Baczek, T. Chemometric Analysis for the Classification of some Groups of Drugs with Divergent Pharmacological Activity on the Basis of some Chromatographic and Molecular Modeling Parameters. Comb. Chem. High Throughput Screen. 2018, 21, 125–137.
- Harshman, R.A.; Hong, S.; Lundy, M.E. Shifted factor analysis—Part I: Models and properties. J. Chemometr. 2003, 17, 363–378.
- Hong, S. Warped factor analysis. J. Chemom. 2009, 23, 371–384.
- Zhou, Y.; Wilkinson, D.; Schreiber, R.; Pan, R. Large-Scale Parallel Collaborative Filtering for the Netflix Prize. In Algorithmic Aspects in Information and Management; Springer: Berlin/Heidelberg, Germany, 2008; pp. 337–348.
- Chernyshov, D.; Van Beek, W.; Emerich, H.; Milanesio, M.; Urakawa, A.; Viterbo, D.; Palin, L.; Caliandro, R. Kinematic dif-fraction on a structure with periodically varying scattering function. Acta Cryst. A 2011, 67, 327–335.
- Urakawa, A.; Van Beek, W.; Monrabal-Capilla, M.; Galán-Mascarós, J.R.; Palin, L.; Milanesio, M. Combined, Modulation Enhanced X-ray Powder Diffraction and Raman Spectroscopic Study of Structural Transitions in the Spin Crossover Material [Fe(Htrz)2(trz)](BF4)]. J. Phys. Chem. C 2011, 115, 1323–1329.
- Uschmajew, A. Local Convergence of the Alternating Least Square Algorithm for Canonical Tensor Approximation. J. Matrix Anal. Appl. 2012, 33, 639–652.
- Comona, P.; Luciania, X.; De Almeida, A.L.F. Tensor decompositions, alternating least squares and other tales. J. Chemom. 2009, 23, 393–405.
- Malinowski, E.R. Theory of the distribution of error eigenvalues resulting from principal component analysis with applica-tions to spectroscopic data. J. Chemom. 1987, 1, 33–40.
- Malinowski, E.R. Statistical F‐tests for abstract factor analysis and target testing. J. Chemom. 1989, 3, 49–60.
- Guttman, L. Some necessary conditions for common factor analysis. Psychometrika 1954, 19, 149–161.
- Kaiser, H.F. The application of electronic computers to factor analysis. Educ. Psychol. Meas. 1960, 20, 141–151.
- Caliandro, R.; Guccione, P.; Nico, G.; Tutuncu, G.; Hanson, J.C. Tailored Multivariate Analysis for Modulated Enhanced Dif-fraction. J. Appl. Cryst. 2015, 48, 1679–1691.
- Silverman, B.W. Smoothed functional principal components analysis by choice of norm. Ann. Stat. 1996, 24, 1–24.
- Chen, Z.‐P.; Liang, Y.‐Z.; Jiang, J.‐H.; Li, Y.; Qian, J.‐Y.; Yu, R.‐Q. Determination of the number of components in mixtures using a new approach incorporating chemical information. J. Chemom. 1999, 13, 15–30.
- Dharmayat, S.; Hammond, R.B.; Lai, X.; Ma, C.; Purba, E.; Roberts, K.J.; Chen, Z.-P.; Martin, E.; Morris, J.; Bytheway, R. An Examination of the Kinetics of the Solution-Mediated Polymorphic Phase Transformation between α- and β-Forms of l-Glutamic Acid as Determined Using Online Powder X-ray Diffraction. Cryst. Growth Des. 2008, 8, 2205–2216.
- Turner, T.D.; Caddick, S.; Hammond, R.B.; Roberts, K.J.; Lai, X. Kinetics of the Aqueous-Ethanol Solution Mediated Trans-formation between the Beta and Alpha Polymorphs of p-Aminobenzoic Acid. Cryst. Growth Des. 2018, 18, 1117–1125.