Note: The following contents are extract from your paper. The entry will be online only after author check and submit it.

1. Introduction

In recent decades, a huge number of engineering structures such as various civil structures (e.g., bridges, dams, buildings, etc.), rotating machines, aircraft, etc., have been designed and widely used in real life-services [1]. Such structures, with either simple or complex geometric or material properties, are subjected to different levels of vibrations from numerous sources, including earthquakes, wind loads, vehicle motions, imbalance of rotating machines, etc. [2]. Excessive levels of vibrations largely affect the performance, health condition, and serviceability of structures and even lead to structural instability and failures [3].

In general, structural damping is a preferable dynamic characteristic able to reduce the degree of system vibrations to an acceptable level [4]. Damping and its variation occur due to the continuous dissipation of energy [5], both internally and externally, linked with factors such as material degradation, geometrical changes, boundary conditions, etc. [6]. With complex mechanisms, structural damping is commonly classified into three types. First, the fluid damping, which originates from hydrodynamic or aerodynamic forces surrounding the structures [7]. Second, the material damping, which appears due to complex atomic-molecular interactions inside materials [8]. Third, the structural damping, resulting from Coulomb friction between parts within a structural system [9]. For damping characterization, several simplified models have been suggested; for instance, viscous damping, hysteretic damping, and Coulomb frictional damping models [10]. In real applications, equivalent viscous damping is commonly used to model the overall behavior of damped systems [11].

Most structural systems show a certain extent of nonlinearity associated with different sources [12,13]. However, neglecting the nonlinearity is acceptable in many cases for the sake of simplification of analysis [14,15]. In other cases, nonlinear behavior plays a dominant role. Nonlinearity neglection should be prevented in such cases, as it may lead to erroneous predictions of system behaviors [16]. Among the causes of system nonlinearity, nonlinear damping [17,18] is often regarded as the most influential; this complexity of which makes it challenging to perform system identification [19]. Moreover, to better accommodate the development of advanced material with strong nonlinear behavior, research on the impact of nonlinear damping is of increasing importance [20–22].

Some damping identification approaches, theoretical and experimental, have been developed [23]. Experimental techniques for damping estimation show advantages in accuracy and reliability. Damping identification approaches provide straightforward explanations for damping properties as compared with theoretical approaches [24]. The enhancement technique of engineering structures is carried out by measuring inputs and outputs during the experiment of real structures. This enhancement technique is made to avoid unwanted behavior of the system subject to damping effects [25].

Several hypotheses can be used for linear and nonlinear damping of low-damping systems [26–28]. High-damping systems usually involve structural damage [29]; however, nonlinear effects on vibrating systems cannot be neglected because of their significant impact on dynamic behaviors [30] [31]. Linear damping approaches can provide precise structural numerical predictions [32,33]. Nevertheless, in numerous modern applications, the effectiveness of these methods cannot be guaranteed, especially when the structures are complex, e.g., composed of composite materials or operating in a hostile environment [34,35]. Therefore, linear methods should be limited to identifying damping in specific simple structures that operate under normal conditions [36]. These drawbacks have, in the last decade, contributed to the rapid development of nonlinear damping methods [37,38].

Damping identification is a challenging task [39] performed by developing a variety of analytical [40–42] and experimental methods of linear and nonlinear systems [43–45]. Moreover, NDI is a practical aspect being conducted to prevent structural failure and tragic events caused by structural damages [46,47]. In addition to enhancing the safety and maintenance of key structures, it also contributes to the control of systems and predicting structural systems responses under nonlinear damping properly [48,49].

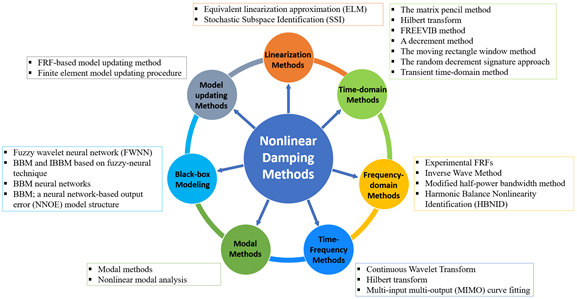
NDI for dynamic systems can be classified into seven categories: Linearization methods, time-domain methods, frequency-domain methods, time-frequency methods, modal methods, black-box modeling, and model updating methods [1]. Classification can also be made from other perspectives, for example, parametric and non-parametric [50,51]. An example of linearization methods is the equivalent linearization approximation (ELA), which is a common method used in applications such as a spring-suspended sectional model system. ELA is utilized for bridges and aeroelastic systems and dampers and shock absorbers used in control systems [52].

The time-domain methods are well-known methods such as the log decrement method used in lightly damped systems and aeroelastic systems [53,54]. In addition, the Hilbert transform (HT) is used to analyze vibration systems [55], heat exchangers, and damage detection of reinforced concrete (RC) structures and composite materials [56,57]. The frequency-domain methods are known by their mathematical simplicity and ability to provide insightful interpretation [58]. For example, harmonic balance nonlinearity identification (HBNID) was employed in systems such as civil engineering, actuators, bioengineering devices, sensors, and robotics [59]. Furthermore, the frequency response functions (FRFs) have been widely utilized to study nonlinear damping in adhesive joints [60,61].

Time-frequency methods, e.g., those based on continuous wavelet transform (CWT), are powerful tools used in applications such as vibration absorbers that are broadly used in naval architecture, rotor-bearing systems, and constructions [62]. In addition, HT was employed in applications such as unbalance of rotating machines, ship movement control, and damage detection of RC beams based on free vibration measurements for nonlinear damping determination [63]. Modal methods are considered particularly useful in the field of structural dynamics and damage identification. The resonant decay method (RDM) was applied to investigate the nonlinear damping in civil, aircraft, and various types of dampers [23]. The wavelet transform (WT) was used in instantaneous damping coefficient identification for damage detection in concrete, automotive, aerospace, and simple built-up structures comprising two bolted beams [64]. Black-box modeling (BBM) is an accurate and efficient method in describing the dynamic behaviors of structures. For example, a fuzzy wavelet neural network (FWNN) was used for nonlinear identification in systems such as vehicle magnetorheological (MR) fluid dampers, aeroelastic systems, modern industries, control systems, and military and defense equipment [65].

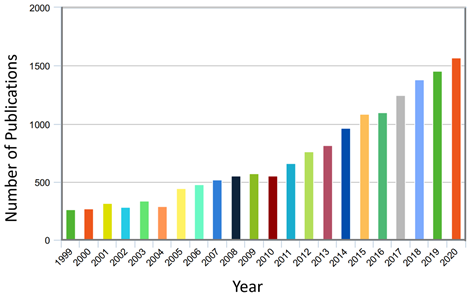
Model updating methods include, for instance, the identification of structural damping using the FRF-based model updating method and damping identification for accurate prediction of the measured FRFs using finite element updated models of the mechanical system [66,67]. Recently, several studies were conducted on dynamic systems. These studies showed the high feasibility of the NDI methods compared to the linear methods because they give more reliable results despite their difficulty [1]. The nonlinear research focuses primarily on the development of efficient and functional methods for reacting to nonlinear structural damping as a fundamental scientific and technological problem. A survey of available research in the engineering community has provided many studies of nonlinear damping, as shown in Figure 1. It is expected that interest from researchers in this field will continue.

Figure 1. The number of publications for nonlinear damping studies (According to the Scopus engine system in the duration from January 1999 to November 2020).

2. Nonlinear Damping Identification Methods

The early study on the identification of nonlinearity of structural models can be traced back to 1970s [1]. The objective of this section is to survey the NDI methods that evolved over the last few years as a result of the development of novel industrial materials and structures [68]. Various nonlinear factors have led to different systems’ behaviors, which means that each system has unique behavior and therefore requires a different approach [69]. Relevant studies were first focused on single-degree of freedom (SDOF) systems [70]. Then, with the advancement of computational techniques, studies were extended to more complex, multi-degree of freedom (MDOF) systems [71–73]. Specific structural types under investigation include bridges, tall buildings, aircraft, etc. [74]. Apart from previous review articles that are mainly about nonlinear system identification [1,2,23], the focus of this study resides on the development of various NDI methods. The methods can be classified into seven categories, as shown in Figure 2.

Figure 2. Nonlinear damping identification methods.

This entry is adapted from the peer-reviewed paper 10.3390/s20247303