Assembly theory was formulated in 2017^[1], introducing the concept of assembly index (initially called "pathway complexity") of an object as the smallest number of steps required to assemble this object from a set of basic building units, forming an initial assembly pool, and from subunits that entered the assembly pool in previous assembly steps. The assembly index is, therefore, a measure of the complexity of the object, which is computable^[2], unlike Kolmogorov complexity, for example, and captures the structural information about the object, unlike Shannon entropy. The theoretical background for the theory was researched^[2] based on directed multigraphs, showing that the assembly index of an object is computable for all finite objects. In particular, determining the assembly index is NP-complete^[3].

Consider two binary strings C = [01010101] and D = [00010111] and the initial assembly pool containing two bits 0 and 1. Both strings have the same length N = 8 and the same Shannon entropy H(C) = H(D) = log₂(2) = 1. However, the assembly index of the first string is a(C) = 3 (In step 1, assemble "01" and put it into the assembly pool, in step 2 assemble "01" with "01" taken from the assembly pool and put "0101" into the assembly pool, and in step 3 assemble "0101" assembled in the second step with "0101" taken from the assembly pool), while the assembly index of the second string is a(D) = 6, since only the substring "01" can be reused from the assembly pool^[4].

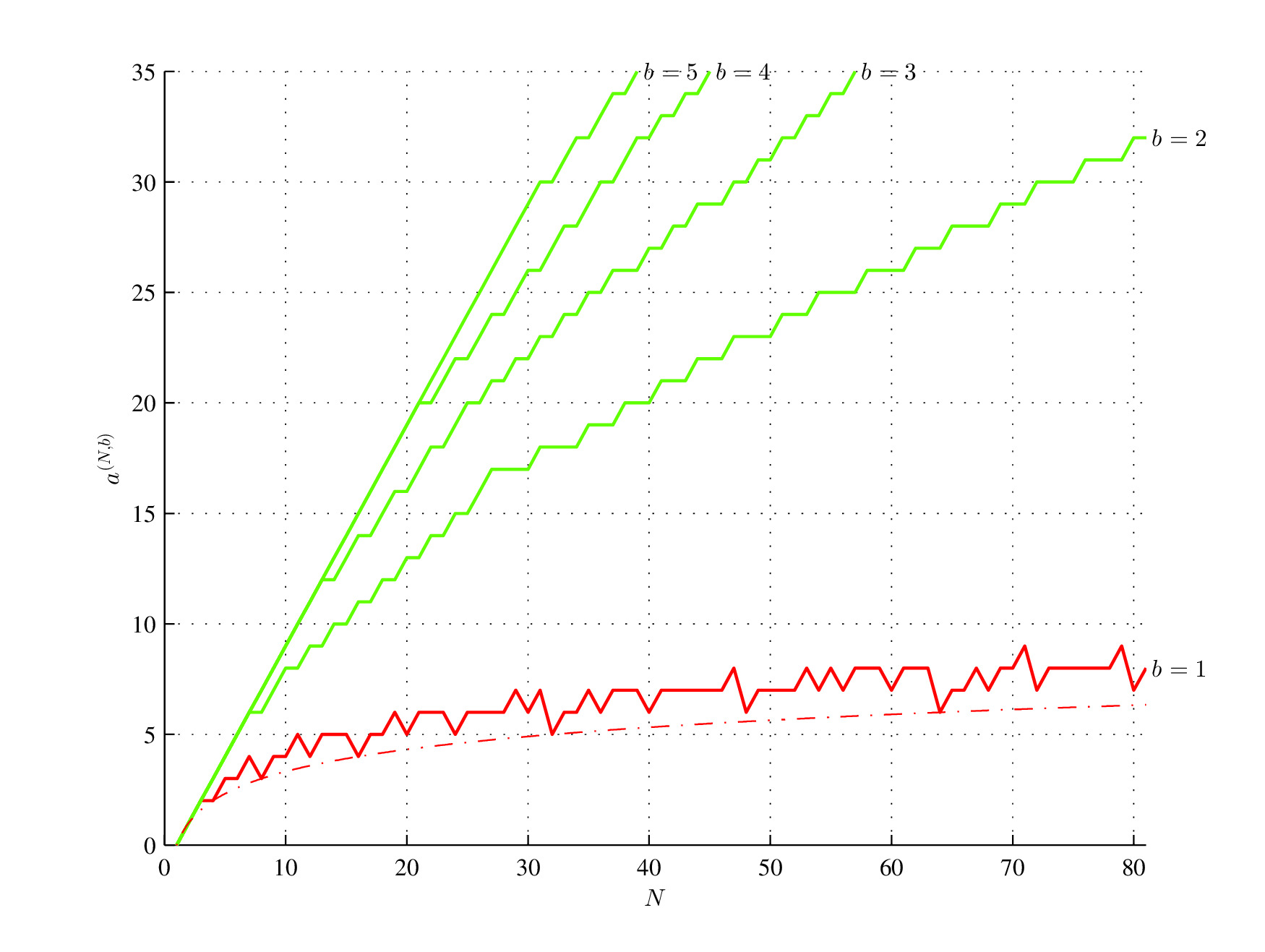
Minimum (red; log₂(N), red, dash-dot) and maximum (green) assembly index for 1 ≤ b ≤ 5 and 0 < N ≤ 81. N is the string length; b is the alphabet size.

Basic building units depend on a particular application of the assembly theory. In chemistry, it has found applications in drug discovery^[5]. Furthermore, the theoretical value of the assembly index of a molecule, where the initial assembly pool contains chemical bonds, can be experimentally confirmed using tandem mass spectrometry, nuclear magnetic resonance, or infrared spectroscopy^[6][7]. Therefore, the assembly index is the universal threshold between abiotic and biotic molecules and a robust, simple biosignature for distinguishing random, abiotic objects from biologically or technologically assembled ones, as only biotic samples can have an assembly index above 15. The more complex a given object, the less likely an identical copy can exist without some information-driven mechanism that generates that object^[8].