Count Random Variables | Encyclopedia MDPI

Count Random Variables: History

View Latest Version

Please note this is an old version of this entry, which may differ significantly from the current revision.

Subjects: Mathematics, Applied

Contributor:

Sandra Mendonça

António Alberto Oliveira

Dinis Pestana

Maria Luísa Rocha

The observation of randomness patterns serves as guidance for the craft of probabilistic modelling. The most used count models—Binomial, Poisson, Negative Binomial—are the discrete Morris’ natural exponential families whose variance is at most quadratic on the mean, and the solutions of Katz–Panjer recurrence relation, aside from being members of the generalised power series and hypergeometric distribution families, and this accounts for their many advantageous characteristics. Some other basic count models are also described, as well as models with less obvious but useful randomness patterns in connection with maximum entropy characterisations, such as Zipf and Good models. Simple tools, such as truncation, thinning, or parameter randomisation, are straightforward ways of constructing other count models.

discrete models
count random variables
Panjer’s family
hierarchical models

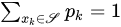
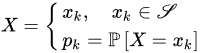
For any $S = {\{x_{k}\}}_{k \in K}$ , with $K \subseteq N_{0} = \{0, 1, \dots\}$ , and for any sequence ${p_{k}}_{k \in K}$ such that $p_{k} \geq 0$ for any $k \in K$ and

$\sum_{x_{k} \in S} p_{k} = 1$

is a discrete lattice random variable with support $S$ and probability mass function ${\{p_{k}\}}_{k \in K}$ . If $x_{k} = k \in N_{0}$ , X is a count random variable.

In most cases, the probability mass function

{\{p_{k}\}}_{k \in K}

is not interesting, since it is difficult to deal with and there is no clear interpretation of the pattern of randomness it describes. The craft of probabilistic modelling (Gani (1986) [1]) uses a diversity of criteria to describe and select models, namely, those arising from randomness patterns (such as counts in Bernoulli trials, sampling with or without replacement, and random draws from urns). Another source of the rationale description of count models are characterisation theorems based on structural properties (e.g., a power series distribution with mean = variance, or maximum Shannon entropy with prescribed arithmetic and/or geometric mean). Recurrence relationships (for instance,

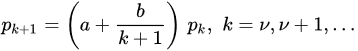) or mathematical properties (for instance, the variance being at most a quadratic function of the expectation) also define interesting families of discrete random variables. On the other hand, asymptotic properties such as arithmetic properties, namely, infinite divisibility, discrete self-decomposability, and stability, serve as guidance in model choice.

This entry is adapted from the peer-reviewed paper 10.3390/encyclopedia4030089

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.