The Łukaszyk–Karmowski metric (LK-metric) defines a distance between two random variables or vectors. LK-metric is not a metric as it does not satisfy the identity of indiscernibles axiom of the metric; for the same random variables, its value is greater than zero, providing they are not both degenerated.
- distance functions
- identity of indiscernibles
- ugly duckling theorem
1. Introduction
LK-metric[1] between two continuous random variables X and Y having a joint probability density function (PDF) F(x,y) is defined as
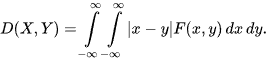
If X and Y are independent, then
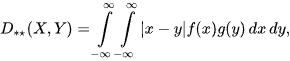
where f(x) and g(y) are PDFs of X and Y, and subscripts denote their types. For example, if X and Y have normal PDFs having the same standard deviation σ but different means μx, μy, then
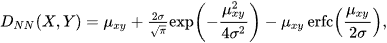
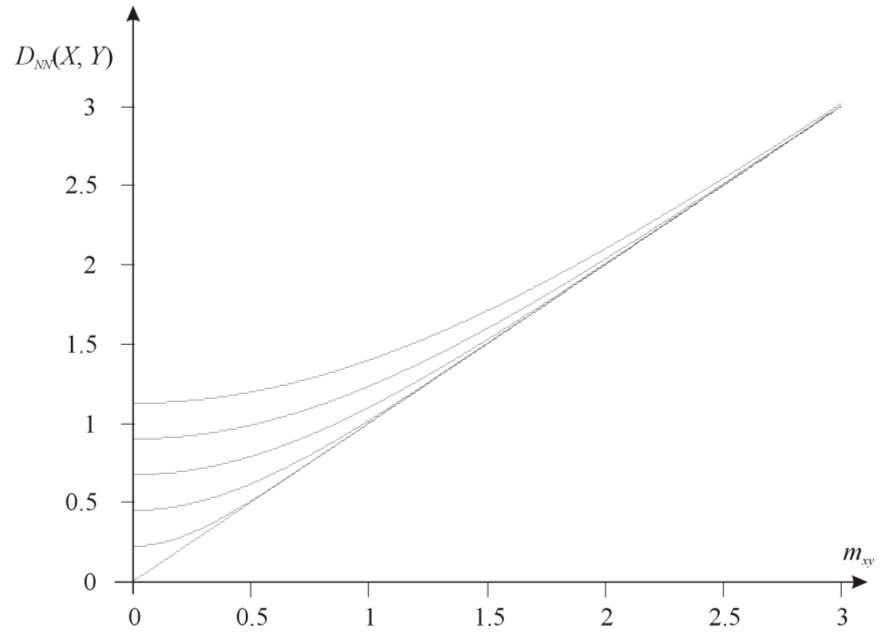
LK-metric between two random variables having normal PDFs and the same standard deviations σ = {0, 0.2, 0.4, 0.6, 0.8, 1}.
where μxy=|μx-μy|. For discrete X and Y, LK-metric has a form
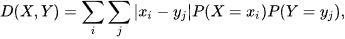
and for random vectors X and Y, LK-metric becomes
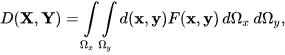
where d(x,y) is a metric function, such as the Euclidean metric. In case, X and Y are mutually and internally independent, a simplified form of LK-metric can also be defined as
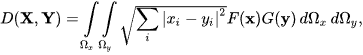
If X and Y are degenerated, almost sure variables having the Dirac delta (or one-point, in the discrete case) PDFs, then LK-metric becomes the metric between their mean values.
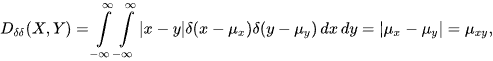
and obviously
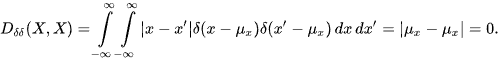
However, in any other case
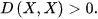
LK-metric satisfies all the remaining axioms of the metric. It is symmetric by definition, and it satisfies the triangle inequality
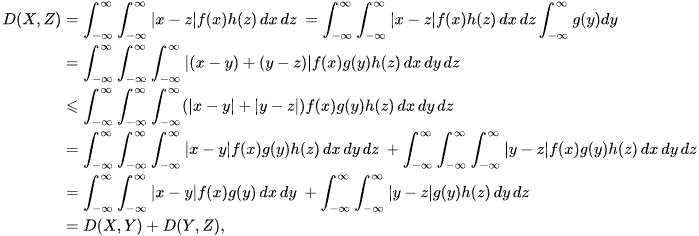
Thus
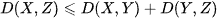
since
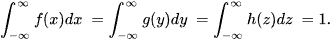
LK-metric is not the only distance function that does not satisfy the identity of indiscernibles axiom[2]. For example, the partial metric[3] also allows each object not necessarily to have zero distance from itself. However, the partial metric satisfies two additional axioms of small self-distances and modified triangle inequality, which are not satisfied by LK-metric[4]. Remarkably, the identity of indiscernibles ontological axiom, introduced to philosophy by Gottfried Wilhelm Leibniz around 1686, is also invalidated by the ugly duckling theorem[5] stated in 1969 and asserting that every two objects one perceives are equally similar (or equally dissimilar). Consequently, the identity of indiscernibles is neither a logical nor empirical principle.
This characteristic non-zero distance effect built in LK-metric allows to avoid ill-conditioning problems in radial basis function interpolation[6][7] and inverse distance weighting[8][9][10][11], where the interpolation accuracy can be improved by choosing the type of distance metric[12][11] and leads to a smooth interpolation function[13]. By preventing zero distances based on parameter uncertainty, LK-metric can, furthermore, be used in analysis of nondeterministic dynamical systems with competing attractors[14]. Since LK-metric represents the mean of distances between all the outcomes of the two uncertain objects, it can also be used in uncertain nearest neighbor classification[15]. The actual value of an uncertain object is modeled by a probability density function[16]. LK-metric has been successfully applied in various fields of science and technology[17][18][19][20][21][22][23][24][13][25][26][27][28][29][30][7][31][32][33][34][35][10][36][37][38][39][40][41][42][43][44][45][11][46][47][48][49][14][50][51].
References
- S. Lukaszyk; A new concept of probability metric and its applications in approximation of scattered data sets. Comput. Mech. 2004, 33, 299-304, .
- Andrzej Tomski; Szymon Łukaszyk; Reply to "Various issues around the L1-norm distance". Ipi Lett. 2024, 2, 1-8, .
- S. G. Matthews; Partial Metric Topology. Ann. New York Acad. Sci. 1994, 728, 183-197, .
- Castro, Pablo Samuel and Kastner, Tyler and Panangaden, Prakash and Rowland, Mark; A Kernel Perspective on Behavioural Metrics for Markov Decision Processes. Transactions on Machine Learning Research 2022, https://openreview.net/forum?id=nHfPXl1ly7, 2835-8856, .
- Satosi Watanabe; Epistemological Relativity. Ann. Jpn. Assoc. Philos. Sci. 1986, 7, 1-14, .
- You-Long Zou; Fa-Long Hu; Can-Can Zhou; Chao-Liu Li; Keh-Jim Dunn; Analysis of radial basis function interpolation approach. Appl. Geophys. 2013, 10, 397-410, .
- Abbas M. Abd; Suhad M. Abd; Modelling the strength of lightweight foamed concrete using support vector machine (SVM). Case Stud. Constr. Mater. 2017, 6, 8-15, .
- M. Gentile; F. Courbin; G. Meylan; Interpolating point spread function anisotropy. Astron. Astrophys. 2012, 549, A1, .
- İ. Bedii Özdemir; A modification to temperature-composition pdf method and its application to the simulation of a transitional bluff-body flame. Comput. Math. Appl. 2018, 75, 2574-2592, .
- Christos Anagnostopoulos; Edge-centric inferential modeling & analytics. J. Netw. Comput. Appl. 2020, 164, 102696, .
- Zhanglin Li; An enhanced dual IDW method for high-quality geospatial interpolation. Sci. Rep. 2021, 11, 1-17, .
- You, Hojun and Kim, Dongsu; Development of an anisotropic spatial interpolation method for velocity in meandering river channel. J. Korea Water Resour. Assoc. 2017, 50, 1023, .
- Petar Durdevic; Leif Hansen; Christian Mai; Simon Pedersen; Zhenyu Yang; Cost-Effective ERT Technique for Oil-in-Water Measurement for Offshore Hydrocyclone Installations. IFAC-PapersOnLine 2015, 48, 147-153, .
- Kaio C. B. Benedetti; Paulo B. B. Goncalves; Stefano Lenci; Giuseppe Rega; Global analysis of stochastic and parametric uncertainty in nonlinear dynamical systems: adaptative phase-space discretization strategy, with application to Helmholtz oscillator. Nonlinear Dyn. 2023, 111, 15675-15703, .
- Fabrizio Angiulli; Fabio Fassetti; Nearest Neighbor-Based Classification of Uncertain Data. ACM Trans. Knowl. Discov. Data 2013, 7, 1-35, .
- Angiulli, Fabrizio and Fassetti, Fabio; Indexing Uncertain Data in General Metric Spaces. IEEE Transactions on Knowledge and Data Engineering 2012, 24, 1640-1657, .
- James C. Davidson; Seth A. Hutchinson. A Sampling Hyperbelief Optimization Technique for Stochastic Systems; Springer Science and Business Media LLC: Dordrecht, GX, Netherlands, 2009; pp. 217-231.
- Gang Meng; Jane Law; Mary E Thompson; Small-scale health-related indicator acquisition using secondary data spatial interpolation. Int. J. Heal. Geogr. 2010, 9, 50-50, .
- Yingjie Xia; Xingmin Shi; Li Kuang; Junhua Xuan. Parallel geospatial analysis on windows HPC platform; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, United States, 2010; pp. 210-213.
- V. Roshan Joseph; Lulu Kang; Regression-Based Inverse Distance Weighting With Applications to Computer Experiments. Technometrics 2011, 53, 254-265, .
- Fengxiang Xu; Guangyong Sun; Guangyao Li; Qing Li; Crashworthiness design of multi-component tailor-welded blank (TWB) structures. Struct. Multidiscip. Optim. 2013, 48, 653-667, .
- Chanyoung Jun; Subhrajit Bhattacharya; Robert Ghrist. Pursuit-evasion game for normal distributions; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, United States, 2014; pp. 83-88.
- Simon Pedersen; Christian Mai; Leif Hansen; Petar Durdevic; Zhenyu Yang; Online Slug Detection in Multi-phase Transportation Pipelines Using Electrical Tomography∗∗Supported by the Danish National Advanced Technology Foundation through PDPWAC Project (J.nr. 95-2012-3).. IFAC-PapersOnLine 2015, 48, 159-164, .
- Branislav Brutovsky; Denis Horvath; Towards inverse modeling of intratumor heterogeneity. Open Phys. 2015, 13, 103, .
- S. Mohammed Hosseini; Samira Smaeili; Numerical integration of multi-dimensional highly oscillatory integrals, based on eRPIM. Numer. Algorithms 2014, 68, 423-442, .
- Luciana Balsamo; Suparno Mukhopadhyay; Raimondo Betti; A statistical framework with stiffness proportional damage sensitive features for structural health monitoring. Smart Struct. Syst. 2015, 15, 699-715, .
- Bing Han; Xinbo Gao; Hui Liu; Ping Wang. Auroral Oval Boundary Modeling Based on Deep Learning Method; Springer Science and Business Media LLC: Dordrecht, GX, Netherlands, 2015; pp. 96-106.
- J. Park; V. Sreeja; M. Aquino; C. Cesaroni; L. Spogli; A. Dodson; G. De Franceschi; Performance of ionospheric maps in support of long baseline GNSS kinematic positioning at low latitudes. Radio Sci. 2016, 51, 429-442, .
- Grzegorz Lenda; Marcin Ligas; Paulina Lewińska; Anna Szafarczyk; The use of surface interpolation methods for landslides monitoring. KSCE J. Civ. Eng. 2015, 20, 188-196, .
- Jan Koloda; Jurgen Seiler; Andre Kaup; Frequency-Selective Mesh-to-Grid Resampling for Image Communication. IEEE Trans. Multimedia 2017, 19, 1689-1701, .
- Pijus Kasparaitis; Kipras Kančys; Phoneme vs. Diphone in Unit Selection TTS of Lithuanian. Balt. J. Mod. Comput. 2018, 6, 162-172, .
- Jorge Vicent; Jochem Verrelst; Juan Pablo Rivera-Caicedo; Neus Sabater; Jordi Munoz-Mari; Gustau Camps-Valls; Jose Moreno; Emulation as an Accurate Alternative to Interpolation in Sampling Radiative Transfer Codes. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 4918-4931, .
- Matthew J. Lake; Marek Miller; Ray F. Ganardi; Zheng Liu; Shi-Dong Liang; Tomasz Paterek; Generalised uncertainty relations from superpositions of geometries. Class. Quantum Gravity 2019, 36, 155012, .
- Aimilios Sofianopoulos; Mozhgan Rahimi Boldaji; Benjamin Lawler; Sotirios Mamalis; Investigation of thermal stratification in premixed homogeneous charge compression ignition engines: A Large Eddy Simulation study. Int. J. Engine Res. 2018, 20, 931-944, .
- D. J. Tan; D. Honnery; A. Kalyan; V. Gryazev; S. A. Karabasov; D. Edgington-Mitchell; Equivalent Shock-Associated Noise Source Reconstruction of Screeching Underexpanded Unheated Round Jets. AIAA J. 2019, 57, 1200-1214, .
- Xiaohui Chen; Qing Zhao; Fei Huang; Rongzu Qiu; Yuhong Lin; Lanyi Zhang; Xisheng Hu; Understanding spatial variation in the driving pattern of carbon dioxide emissions from taxi sector in great Eastern China: evidence from an analysis of geographically weighted regression. Clean Technol. Environ. Policy 2020, 22, 979-991, .
- Helin Gong; Yingrui Yu; Qing Li; Chaoyu Quan; An inverse-distance-based fitting term for 3D-Var data assimilation in nuclear core simulation. Ann. Nucl. Energy 2020, 141, 107346, .
- Liming Xu; Xianhua Zeng; He Zhang; Weisheng Li; Jianbo Lei; Zhiwei Huang; BPGAN: Bidirectional CT-to-MRI prediction using multi-generative multi-adversarial nets with spectral normalization and localization. Neural Networks 2020, 128, 82-96, .
- Zhanglin Li; Xialin Zhang; Rui Zhu; Zhiting Zhang; Zhengping Weng; Integrating data-to-data correlation into inverse distance weighting. Comput. Geosci. 2019, 24, 203-216, .
- Wei Wei; Zecheng Guo; Liang Zhou; Binbin Xie; Junju Zhou; Assessing environmental interference in northern China using a spatial distance model: From the perspective of geographic detection. Sci. Total. Environ. 2020, 709, 136170, .
- Yiyuan Han; Bing Han; Zejun Hu; Xinbo Gao; Lixia Zhang; Huigen Yang; Bin Li; Prediction and variation of the auroral oval boundary based on a deep learning model and space physical parameters. Nonlinear Process. Geophys. 2020, 27, 11-22, .
- Yuying Lin; Xisheng Hu; Mingshui Lin; Rongzu Qiu; Jinguo Lin; Baoyin Li; Spatial Paradigms in Road Networks and Their Delimitation of Urban Boundaries Based on KDE. ISPRS Int. J. Geo-Information 2020, 9, 204, .
- Aimilios Sofianopoulos; Mozhgan Rahimi Boldaji; Benjamin Lawler; Sotirios Mamalis; John E Dec; Effect of engine size, speed, and dilution method on thermal stratification of premixed homogeneous charge compression–ignition engines: A large eddy simulation study. Int. J. Engine Res. 2019, 21, 1612-1630, .
- Panagiotis Pergantas; Nikos E. Papanikolaou; Chrisovalantis Malesios; Andreas Tsatsaris; Marios Kondakis; Iokasti Perganta; Yiannis Tselentis; Nikos Demiris; Towards a Semi-Automatic Early Warning System for Vector-Borne Diseases. Int. J. Environ. Res. Public Heal. 2021, 18, 1823, .
- Mobeen Akhtar; Yuanyuan Zhao; Guanglei Gao; An analytical approach for assessment of geographical variation in ecosystem service intensity in Punjab, Pakistan. Environ. Sci. Pollut. Res. 2021, 28, 38145-38158, .
- Bogdan-Mihai Negrea; Valeriu Stoilov-Linu; Cristian-Emilian Pop; György Deák; Nicolae Crăciun; Marius Mirodon Făgăraș; Expansion of the Invasive Plant Species Reynoutria japonica Houtt in the Upper Bistrița Mountain River Basin with a Calculus on the Productive Potential of a Mountain Meadow. Sustain. 2022, 14, 5737, .
- Fabio Saggese; Vincenzo Lottici; Filippo Giannetti; Rainfall Map from Attenuation Data Fusion of Satellite Broadcast and Commercial Microwave Links. Sensors 2022, 22, 7019, .
- Zhiguang Han; Jianzhang Xiao; Yingqi Wei; Spatial Distribution Characteristics of Microbial Mineralization in Saturated Sand Centrifuge Shaking Table Test. Mater. 2022, 15, 6102, .
- Oludayo Ayodeji Akintunde; Chidi Vitalis Ozebo; Kayode Festus Oyedele; Groundwater Quality around upstream and downstream area of the Lagos lagoon using GIS and Multispectral Analysis. Sci. Afr. 2022, 16, e01126, .
- A. A. El-Atik; Y. Tashkandy; S. Jafari; A. A. Nasef; W. Emam; M. Badr; Mutation of DNA and RNA sequences through the application of topological spaces. AIMS Math. 2023, 8, 19275-19296, .
- David Hernández-López; Esteban Ruíz de Oña; Miguel A. Moreno; Diego González-Aguilera; SunMap: Towards Unattended Maintenance of Photovoltaic Plants Using Drone Photogrammetry. Drones 2023, 7, 129, .
