The possibility of moving objects accessing different types of points of interest (POI) at specific time is not always the same, so quantitative time geography research needs to consider the actual POI semantic information, including POI attributes and time information.
- time geography
- space–time trajectory
- POI
- semantic information
- position probability
- Introduction
Probabilistic time geography holds that the possibility of moving objects accessing reachable position points is not always the same [1], and is related to the space-time distance between space-time anchor points. The first law of geography states that the closer the space distance between geographic entities, the stronger the correlation. Similarly, in time geography, the lower the time cost to the space-time anchor, the more likely moving objects are to appear. This means that in quantitative in time geography analysis, the closer the time and space distance from the determined space-time anchor point, the greater the probability of moving objects appearing. Therefore, we expect a quantitative measure model of position probability in time geography.
Downs introduced a position probability measurement model that considers space-time distances, known as Time-Geographic Density Estimation (TGDE) [2]. From the perspective of historical experience data, TGDE measures the access probability of the reachable point to be measured by calculating the time cost between two adjacent anchor points in time distance from the reachable point. This method combines kernel density estimation and time geography, and follows the first law of geography to construct a time geographic density estimation model based on geographic ellipse. Consequently, the space-time uncertainty of moving objects between any two time adjacent space-time anchor points can be expressed as a probability density cloud. Such probability density cloud can be used in two aspects: First, kernel density estimation [3], which is the superposition of all density clouds on the space-time trajectory, is used to express the home range estimation of the moving object in the space-time trajectory region; The other is interaction analysis [4], that is, the intersection analysis of density clouds in the same time period, which is used to measure the interaction probability of two moving objects in the space-time trajectory period. Such a probability density cloud modeling method is effective in homogeneous space [5].
However, up to this point, the position probabilistic modeling method of probabilistic time geography still stays in the homogeneous space, only considering the time and space information of the position point, but ignoring the semantic attribute information. This article will make two important extensions. Firstly, the distribution of position probability is extended from feedback to mutual feedback. The classical method of position probability allocation is the calculation of the time cost from the space-time anchor point to the measured point, which is a one-way feedback, only considering the ability constraint of whether the moving object has enough ability to reach the measured point, which refers to the joint constraint of the moving speed and time of the moving object. However, the semantic information of the point to be measured also has an impact on the access of the moving object, such as the moving object will not access the supermarket closed after 22:00 or the access probability is 0, which belongs to the ability constraint. On the basis of considering the time cost of the point to be measured, we will consider the mechanism of the semantics of the point to be measured on the access probability, and form the “Mutual feedback model” of the anchor point and the point to be measured. Then, we also extend the position probability model of homogeneous space to heterogeneous space, especially urban space. In urban space, activity places are often marked with Point of Interest (POI) on the map, so POI can be used to express the space-time position points accessed by moving objects, and in different periods, different types of POI have different attraction to moving objects. POI position points that contain semantic attribute information can have an impact on access to moving objects, such as on weekdays when a child accesses school in the morning instead of going to the park. Therefore, we will have a method for calculating the probability of position in heterogeneous space.
The rest of this article is organized as follows. Section 2 explains the relevant basis and background of this study, including the related concepts of time geography, the introduction of POI and POI in time geography. Section 3 describes in detail the probabilistic time geographic modeling method considering POI semantics, including POI position probability modeling, POI time weight modeling, POI type weight modeling and POI access probability modeling. Section 4 describes the research process of this paper, that is, using the model proposed in Section 3 to calculate the POI access probability considering POI semantics. Section 5 summarizes the research in this paper and discusses potential extensions.
- Related work
This section provides the basic theory of time geography and probabilistic time geography, and discusses the mechanism of interaction between POI and moving objects. Time geography provides an important theoretical framework for measuring the space-time uncertainty of potential access to space-time position points for moving objects [6,7]. Probabilistic time geography is an extension of (classical) time geography [8], paying more attention to the possibility of space-time position points being accessed. These theories will be closely integrated in the work of this paper. In this paper, the space-time semantic information of POI is introduced to reflect the possibility of moving objects accessing POI, that is, the POI position probability measure considering the semantic information.
2.1. Time geography
Time geography studies the space-time uncertainty of moving objects under space-time constraints [9-11]. Space-time constraints can be divided into ability constraints, authority constraints and combination constraints in time geography [8]. Ability constraint means that the ability of the moving object to carry out various activities is limited, such as the moving object has its own maximum moving speed; Authority constraint means that the moving object is restricted by laws, customs and social norms when carrying out activities, such as the activity place is only open during business hours; The combination constraint refers to the interaction between the moving object and other moving objects or activity places when carrying out activities, such as a moving object going to a restaurant-type POI position points for dining [8]. The research of time geography is divided into two categories: qualitative research and quantitative research.
In qualitative research, time geography primarily employs three key concepts: space-time trajectories, space-time prisms, and potential path areas (PPA) to describe space-time uncertainty [12-15]. Space-time trajectories can be viewed as time series of geographic position points, which can be represented in time geography through STP:

where, represents the space-time path (Figure 1), is the total number of trajectory points, and is the trajectory point of the moving object, which can be described as , and respectively represent the two-dimensional space position and time stamp of trajectory points. Trajectory points are sometimes called anchor points or control points. The STP expresses the directional movement trend of the moving object, while the space-time prism can express the space-time boundary of the moving uncertainty. The space-time prism represents the set of all possible space-time points that a moving object can reach under the common constraints of the starting and ending points, the ability constraints (such as the maximum moving speed) and the authority constraints (such as the geographical environment) (Figure 1a). The footprint or projection of the space-time prism in the plane space is called PPA, and in the homogeneous space can be described as an ellipse with the two anchor points as the focal point and as the major axis:
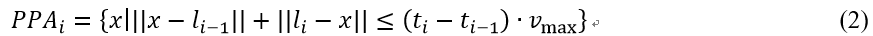
Where, represents PPA on the trajectory segment, represents any point in , represents the Euclidean distance in two-dimensional space, is the budget time of each pair of trajectory anchor points , and is the maximum moving speed of the moving object.
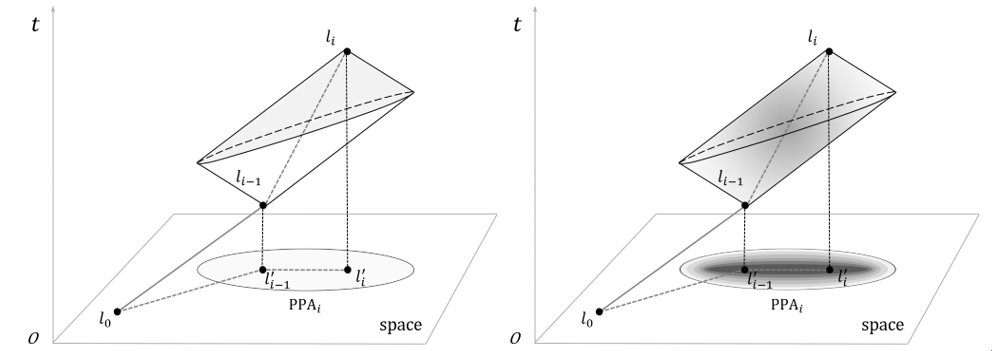
Figure 1. Basic tools of time geography: (a) space-time prism and PPA; (b) probabilistic space-time prism and probabilistic PPA.
In quantitative research, time geography assigns a position probability to each position point within a PPA or space-time prism to represent how likely it is that a moving object will access a certain reachable position at a given time. Therefore, the quantitative research of time geography is also called probabilistic time geography, which is a fusion of time geography and probability theory [8]. The basic idea is: in the PPA or space-time prism during a pair of trajectory anchor points, the position probabilities of moving objects accessing different position points at any time are not always equal, and the size of the probability value changes with the change of state information [16-18]. For any reachable position point, different position probabilities are typically assigned to the position points based on the time cost of reaching that point from the starting and ending points, often using distance decay kernel function models such as Brownian bridge and TGDE [7, 16, 19-21].
The qualitative and quantitative research methods of time geography analyze the space-time uncertainty of moving objects and consider the three space-time constraints of time geography. These methods are valid in homogeneous space, especially when not distinguishing the semantic attributes of position points, such as the type of POI and time semantic information. However, differences in the attachment characteristics of space position points will produce different attractions for moving objects and change over time.
2.2. POI
POI refers to geographic position points on a map that are of interest to moving objects, with information including position, attributes (types), and time [22,23]. People's travel always has certain preference and purpose [24], which is why navigation and planning are essential in people's journeys. POI has gradually become the key search information for people's travel navigation [25], which is related to POI representing certain functions and needs, and therefore has become an important information for human activity analysis [26].
There are significant differences in the attractiveness of different types of POI to individuals. For example, restaurant POI may attract people to eat, tourist attractions POI may attract people to access, transportation facilities POI may affect people's living habits and travel choices, and shopping consumption POI may affect people's consumption behaviors and so on. The space distribution of POI positions usually has a certain aggregation [27]. For example, a large number of various service types of POI are gathered in urban business districts, so as to attract nearby consumers to travel.
The same type of POI will have different attraction to individuals at different time periods [28-30]. For example, the attraction of restaurant POI to individuals at meal time is much higher than that at other time; the attraction of corporate POI to individuals is greater on working days; and the attraction of tourist attraction POI is generally greater on holidays. POI can better reflect the space-time activity behavior of urban residents, and has a strong explanatory power for the behavior of moving objects accessing the space-time position points. Therefore, it is necessary to consider the actual POI semantic information in the quantitative calculation of position probability.
2.3. POI in time geography
Based on the analysis above, it can be concluded that the attractiveness of POI has an impact on the access of moving objects. The quantitative description of this influence will affect the calculation of position probability. The activity of an individual moving object usually includes various POI position points, and there is space-time proximity between the space-time trajectories of moving objects and the accessed POI positions. Existing studies have analyzed the attractiveness of POI from two aspects.
Zeng proposed a method to analyze the change of attraction of urban POI based on taxi track [31]. He calculated the attractiveness and distribution of different categories of POI in different time periods according to the proximity of taxis staying near different categories of POI in different time periods, and then statistically analyzed the law of citizen activities. He believes that the attractiveness of POI is related to its attributes, position, and time period, and that existing methods ignore the influence of time and category on the attractiveness of POI. This method evaluates the attractiveness of POI through statistical analysis, and presents the distribution of POI in a large range of global attractiveness, but ignores the semantic information of POI itself and the personalized attractiveness of POI to a single space-time trajectory. Moreover, this method requires a large number of independent trajectory data samples, and lacks a priori in calculating the probability distribution. Downs assigns access probabilities to space positions including POI positions through TGDE [2], and the access probability of POI positions reflects the attraction of the POI to moving objects. This method only considers the start and end points of space-time trajectories, without considering the time budget of corresponding activities at POI positions. This method also ignores the semantic information of POI, and lacks verification of the posterior probabilities of POI accesses based on empirical data.
The above research indicates that the influence of POI semantic information on the trajectory of moving objects is significantly different, and correspondingly, the possibility of moving objects on the same trajectory accessing POI with different attractiveness is also different. In time geography, on the one hand, the attraction of POI is an uncertainty measure of space-time position points, which is the probability of space-time position statistics through a large number of space-time trajectories. On the other hand, relative to the space-time trajectory, POI is the position point that the moving object can reach in space-time, and the access activity at the POI position point is also a part of the time budget between the anchor points of the space-time trajectory.
Therefore, the time geography based on space-time trajectory to predict space-time uncertainty needs to incorporate the semantic information of POI into the position probability distribution, including POI type and time factor, etc. At present, TGDE only considers the space position and the time cost from the position point to the two anchor points, without considering the difference of POIs in space positions. In this paper, a POI probability model considering the proximity of moving trajectories is proposed based on the known trajectory information and the space-time distance between the trajectory point and the POI. The model expresses the space-time uncertainty between known precise space-time position points based on the space-time constraints of moving speed and time limitations, and provides all the information, including time, space and semantic information, for this space-time uncertainty measurement, which avoids the error caused by single information. This model not only provides a theoretical basis for the quantification of position probability, but also provides a time geography support for the statistics of POI attraction. For example, in the space-time prism of a moving object, the trajectory that does not contain POI can be excluded when calculating the space-time trajectory of a moving object passing through POI.
This entry is adapted from the peer-reviewed paper 10.3390/ijgi13010022
