Microwave Resonators for Wearable Sensors Design

Microwave Resonators for Wearable Sensors Design: History

Please note this is an old version of this entry, which may differ significantly from the current revision.

Contributor:

The field of flexible electronics is undergoing an exponential evolution due to the demand of the industry for wearable devices, wireless communication devices and networks, healthcare sensing devices and the technology around the Internet of Things (IoT) framework. E-textiles are attracting attention within the healthcare areas, amongst others, for providing the possibility of developing continuous patient monitoring solutions and customized devices to accommodate each patient’s specific needs.

textile materials
flexible resonator
textile resonator
wearable device
washing analysis
bending analysis
embroidered resonator

1. Principle of Operation and Classification of Microwave Resonators

1.1. Principle of Operation of Microwave Resonators

By definition, a microwave resonator is a structure based on a series of parallel RLC lumped or quasilumped-element equivalent circuits aimed at confining the electromagnetic energy. Microwave resonators are of interest due to the range of applications they offer, principally filters, oscillators, frequency meters and tuned amplifiers ^[1].

Ideally, a microwave resonator might be prototyped by a simple LC circuit configuration given a frequency close to the resonance ^[2], neglecting the losses.

According to the transmission line theory, in a case where the resonant circuit sizes are multiples of λ at the fundamental frequency (e.g., half-wavelength resonator, λ/2, or quarter-wavelength resonator, λ/4), the result is no longer acknowledged as a lumped element but rather a distributed line resonator.

1.1.1. Resonance Frequency and Quality Factor: A Brief Description

Resonance Frequency, ω₀

In an RLC resonant circuit, the resonance occurs when the magnetic and electric impedances condition is met (X_L = X_C). The resonance frequency, ω₀, is expressed as shown in Equation (1):

Quality Factor, Q

The Q-factor measures the loss of the resonant circuit as the ratio of the resonance frequency to the bandwidth of the circuit, meaning that the higher the Q value, the lower the losses.

The losses in a resonator might have different origins. The Q isolated from any external circuitry effect (without the MUT—Material Under Test—being loaded) is designated as unloaded Q₀. This is the higher Q value for the system.

Equation (2) describes the relation between the loaded Q, the resonance frequency f₀ and the ±3 dB (half-power) bandwidth of the frequency, Δf. The same is illustrated in Figure 1.

Figure 1. Graph of a bandpass filter Q-factor.

The unloaded Q₀ has a logaritmic relation with the inserion loss IL (obtained from S₂₁, measured in dB) as per Equation (3):

Therefore, the loaded Q bandwidth, BW, for a circuit with bandpass properties, is given in Equation (4):

The insertion loss increases for a loaded Q near to an unloaded Q₀, and a higher loaded Q leads to a narrower bandwidth, which can be very lossy. Hence, in order to avoid excessive losses, unloaded Q₀ >> loaded Q.

Since the Q-factor is decisive for the selection of a resonator design (for instance, for filtering applications), multiple configurations have been presented throughout the years in the literature. The length of the lossy transmission line and its termination are the two variables to adjust in order to achieve the desired results.

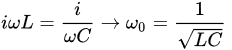
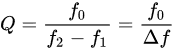
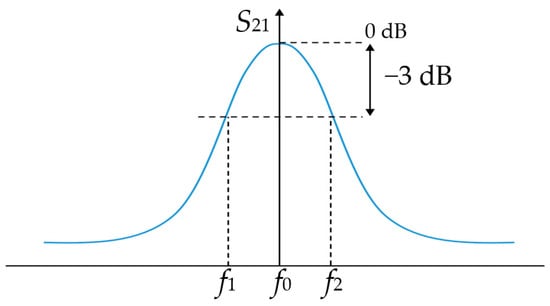
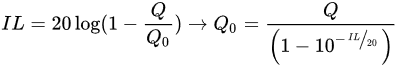
1.1.2. Frequency Variation as a Sensing Principle

The resonators of interest in this article sense the variation of the resonance frequency caused when placing the MUT in the sensing area. These are extensively used for the dielectric characterization of solids, liquids and even gases by studying the relation between the f₀ and the loaded Q with the material’s dielectric constant or permittivity, ε_r.

The resonator consists of a sensing area (where the MUT will be placed) and a transmission line. First, an initial value of the resonance frequency without the MUT f₀ is obtained, and then the transmission line is loaded with the MUT, which causes a variation of the resonance frequency, f₀’. The dielectric properties values are hence obtained by the frequency response shifting of the S₂₁ parameter.

Figure 2 illustrates the frequency variation before and after placing the FUT.

Figure 2. Frequency shift from (a) without MUT to (b) with MUT in the sensing area.

1.2. Classification and Configurations of Resonators

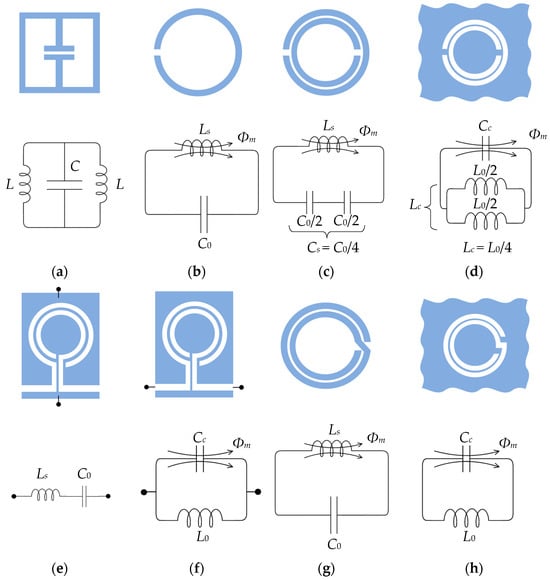
1.2.1. Types of Resonators

Resonators are classified into three main categories: transmission line resonators, waveguide cavity resonators and dielectric resonators. The interest of the present article is the transmission line resonator, specifically the microstrip resonator, which encompasses one or multiple oscillating electromagnetic fields. The transmission line resonant method is a better choice compared to others such as coaxial or waveguide cavity in terms of compactness in size, robustness, elevated sensitivity, and especially because it is easy to fabricate and does not imply the destruction of the MUT. All these benefits make this method the most viable for the design of wearable devices.

These can be classified as below.

○

Lumped-element resonator and quasilumped-element resonator, which resonate accordingly to the aforementioned Equation (1).

○

Distributed line resonators, which resonate at a frequency, f, that is a function of the fundamental resonance frequency, f₀.

Quarter-wavelength (λ/4) resonator (f ≈ (2n − 1) f₀ for n = 2, 3, …) with shunt series or shunt parallel resonance.
Half-wavelength (λ/2) resonator (f ≈ nf₀ for n = 2, 3, …).
Ring resonator, whose resonance frequency is a function of the ring radius, r (2πr = λ, f ≈ nf₀ for n = 2, 3, …).
And others: stepped impedance resonator (SIR), hairpin resonator, etc.

○

Patch resonators, which can be shaped into numerous geometries such as circular or triangular.

Figure 3 illustrates the above-mentioned resonators.

Figure 3. Some microstrip resonator structures: (a) half-wavelength (λ/2) resonator; (b) quarter-wavelength (λ/4) open-end stub resonator; (c) ring resonator; (d) circular patch resonator; (e) stepped impedance resonator; (f) hairpin resonator.

Distributed line resonators can be configured in several ways depending on the filtering requirements. In ring resonators, the symmetrical geometry permits the resonance to befall in any orthogonal coordinate, which is a feature of real interest for the design of dual-mode filters ^[2]. Alternatively, other dual-mode resonating structures have been designed and implemented in both wired and wireless communication methods, such as squared and mender-loop resonators, where this last one is advantageous due to the compact dimensions ^[3].

For sensing purposes, the typical topologies of resonators that are widely employed are listed below:

Electric-LC (ELC);
Ring resonators:

○

Split-ring resonator (SRR);

○

Complementary split-ring resonator (CSRR);

○

Open split-ring resonator (OSRR);

○

Open complementary split-ring resonator (OCSRR);

○

Spiral resonator (SR);

○

Complementary spiral resonator (CSR).

Figure 4 illustrates these topologies and their equivalent circuits.

Figure 4. Topologies of the (a) ELC; (b) single SRR; (c) double SRR; (d) double CSRR; (e) OSRR; (f) OCSRR; (g) SR; (h) CSR; and their equivalent circuit models. The ohmic losses would be considered by adding a series resistance in the model. Models reproduced from references ^[4]^[5].

2. Materials and Methods in Flexible Electronics

Flexible electronics are considered those electronic devices with the capability to alter their planar structure by bending, folding, twisting, stretching and deforming without altering their electrical properties.

The first investigation toward flexible electronics dates back to the 1960s, when a flexible solar cell arrays prototype made of crystal silicon wafer cells assembled on a plastic substrate was presented ^[6].

From then onwards, a huge evolution can be observed in terms of design and materials selection in order to achieve the desirable performance, dimensions and adaptability of the electronic devices to match and supersede the huge market demand.

The materials must prove, at least, exceptional mechanical properties and energy generation and storage. Other promising properties might be water resistance, high adhesion, biodegradability and so forth. The author of ^[7] enumerates the six requirements of flexible substrates:

Optical properties: low birefringence and clear substrates are a must for displays.
Surface roughness: asperities impact on the electrical function.
Thermal and thermomechanical properties: the substrate’s working temperature must support the maximum fabrication process temperature.
Chemical properties: avoid contaminants release.
Mechanical properties: an elevate elastic modulus is necessary to grant the substrate’s bending and stretching.
Electrical and magnetic properties: substrate must either conduct or insulate as per the designs’ requirements.

Multiple layers have to be considered when creating flexible electronic devices: the substrate, the connectors/electrodes and the conductive/functional layers. In ^[8], a classification of intrinsically soft materials for flexible electronics is given. All details are reported in Table 2.

Table 2. Intrinsically soft materials for flexible electronics ^[8].

Layer	Applications	Materials
Substrate Materials	Polymers	PVA, PET, PI, PU, PE
	Flexible and stretchable	PEN, PDMS
	Eco-friendly and biodegradable	Paper, chitin, silk, gelatin
Electrode Materials	Soft metals	Galinstan alloy, metal nanoparticles and nanowires
	Conductive nanomaterials	Carbon materials: graphene, carbon nanotube
	Conductive polymers	PEDOT: PSS, PANI
	Hybris materials	Carbon/metal, polymer/metal
Functional Materials	Cluster materials	Molecules, polymers, biomass
	Low-dimensional and nanomaterials	Nanoparticles and Quantum dots Nanowires, nanotubes and nanoribbons Graphene, transmission metal dichalcogenides and mXenes
	Organic–inorganic hybrid materials	Nanomaterials/polymers

2.1. Conventional Substrates

Traditionally, three different types of materials are used as substrates for flexible applications: metals, organic polymers and thin glass. Their properties are compared in Table 3.

Table 3. Properties of substrates: metal foil, plastic film and thin glass ^[8]^[9]^[10].

Property	Metal Foil	Plastic Film	Thin Glass
Thickness, t	Stainless steel 430 100 μm	PEN, PI 100 μm	Glass 1737 100 μm
Flexibility	At t < 125 μm	High	At t < 100 μm
Young’s modulus, E	Stainless steel 430 200 gPa	PEN, PI 5 gPa	Glass 1737 70 gPa
Optical transmission visible	Opaque	PEN and PET semitransparent (optical transmittance >85%)	Semitransparent (optical transmittance >90%)
Resistance to process chemicals	High (Stainless steel)	Poor for PC, PES, PAR, PCO	Resistance to most of them
Dimensional stability	High	Lower than glass	High
Temperature tability	High	Lower than glass	High
Temperature tolerance	≤1000 °C	≈200 °C	≤600 °C
Thermal conductivity	Stainless steel 430 16 W/m°C	PEN, PI 0.1–0.2 W/m°C	Glass 1737 1 W/m°C
Electrical conductivity	Conductive Insulation requires insulating layer coating	Insulator (Except ICPs)	Insulator
CTE ¹	Low (<20 ppm/°C) (Stainless steel 430, 304)	Low (<20 ppm/°C) (PET, PEN, PI)	Low (≈4 × 10⁻⁶ ppm/°C)
Surface roughness	≈1 μm	≈10 μm	≤1 μm
Durability	High	Lower than metal	Lower than metal
Permeability against oxygen and water	Impermeable	Easily permeated by oxygen and water	Impermeable
Roll-to-toll processable	Yes	Likely	Not likely

¹ Coefficient of thermal expansion.

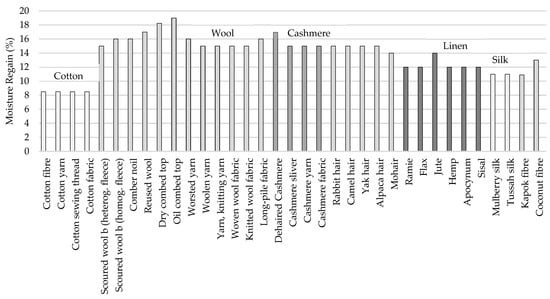
2.2. E-Textiles

Given the increase in the manufacturing demand for wearable electronics for body area networks (BANs), the industry is working on the usage of textiles so these can be employed for the design of clothes, shoes and other accessories such as wristwatches. Textiles have been of strong interest in health since the 1990s for the constant monitoring of patient vitals and activities such as electrocardiography, electromyography and electroencephalography. Textile-based electrodes and sensors can be employed for sensing strain, pressure, temperature, heat flux, sweat, humidity, and even gas detection ^[11].

According to ISO-TR-23383-2020 ^[12], there is a differentiation between the electrically conductive textiles and the smart textiles (e-textiles): electrically conductive textiles are defined as textiles with integrated e-circuits made of conductive fibers, whereas e-textiles are textile-based products with electronics embedded on them.

2.2.1. Key Properties of Textiles in Electronics

The huge range of fabrics and their particular properties offers the flexibility to select the best choice for each specific application and its desired performance. Several are found in the literature investigating the RF applications (mainly the design of antennas and resonators) on fabric substrates. One of the most commonly used materials is felt, but there are others like goch, leather, jeans, cotton, silk, wax or even combinations of those ^[13].

In order to not compromise the performance of the sensing device, it is crucial to study and select the appropriate textile. Depending on the industry demand and the applications, some intrinsic properties will be more instrumental than others, either enhancing the electrical capacity and/or granting mechanical features and quality.

Relative Permittivity and Loss Tangent

By definition, the relative permittivity, ε_r (also known as ‘dielectric constant’, k) determines the ability to polarize a material when exposed to an electrical field ^[14]. In other words, this is an intrinsic material’s parameter that indicates its capacity to store energy when applying a potential across it ^[14].

The relative permittivity represents the real part of the complex dielectric permittivity,

ε

_r, which is expressed as shown in Equation (5):

where the permittivity of vacuum,

ε_{0}

, has a value of 8.854 × 10⁻¹² F/m. The loss tangent, tanδ, is the relation between both the imaginary and the real part, which quantifies the material losses. A small loss tangent (tanδ << 1) is found in low-loss dielectric materials, whereas a large loss tangent (tanδ >> 1) is inherited in lossy dielectrics that demonstrate a limited capacity to store energy ^[11].

The loss tangent is expressed in Equation (6):

Hence, these two parameters are certainly decisive in the selection of a material for RF microwave applications.

Relative Humidity and Regain

Relative humidity, RH, expresses in percentage the ratio of a water–air mixture against the saturation humidity ratio at a specific temperature.

Moisture regain, MR, expresses the moisture absorption, in other words, the capability to absorb water or moisture from the environment, which is also a percentage. Figure 5 exposes the moisture regains of some natural fibers, according to ^[15]. Others of interest are found in ^[16]^[17].

Figure 5. Moisture regains (%) of natural fibers ^[15]^[16]^[17].

Both relative humidity and temperature have a huge impact on the fibers’ physical properties such as dielectric constant, tensile strength, electrical resistance, rigidity or elastic recovery. The effects will be more notorious in natural and hydrophilic fibers than synthetic polymeric fibers, which are hydrophobic.

In ^[18], a breaking load test is performed on cotton, polyester and silk samples to compare the effect of the relative humidity on the tensile strength of the fabrics. The results prove that silk and cotton are highly conditioned by the moisture in the environment due to their hydrophilic nature, which results in an evident degradation of their fibers in the case of silk, whereas cotton tends to increase the strength the higher the RH is. This is explained by the cellulosic properties of the material, which permit the release of internal strain by swelling, resulting in a uniform distribution of stress.

In the case of polyester, due to its hydrophobic characteristics and crystalline structure, the tensile strength remains almost unaltered along the different relative humidities.

Relative humidity also has an influence on the electrical properties, in a sense that the presence of moisture alters the relative permittivity, ε_r: the higher the RH is, the more the ε_r increases (due to the bigger presence of water, which has a relative permittivity value around 78.4 ^[19]).

In ^[20], a study over five samples is performed to analyze the influence of the relative humidity in the electrical properties of fabrics for antenna design. A quadratic relation between the RH and the ε_r is expressed in Equation (7), which explains how the relative permittivity increases more in accordance with the relative humidity on materials that are naturally more absorbent.

It is also observed in the aforesaid article that the frequency is shifted to lower frequencies as the relative permittivity increases, and the frequency peak widens and flattens as a consequence of additional losses.

Surface Resistance, Surface Resistivity and Conductivity

Surface resistance, R_s, defines the capacity that a material has to resist the electricity flow. In other words, it is the relation between the DC voltage and the current that flows between two electrodes, according to Ohm’s law. It is measured in Ohms (Ω).

The surface resistivity, ρ_s, is the resistance to current leakage along an insulating material’s surface. Its measurement is in Ohm/square (Ω/sq.) ^[21].

Electrical conductivity or conductance, σ, is defined as the electrical conduction, meaning the material’s ability to transfer current. The SI unit of conductivity is Siemens per meter (S/m) ^[22].

These three parameters are related in that the conductivity is inversely proportional to the surface resistivity per a given thickness, t, as shown in Equation (8).

For this reason, it is so important when selecting the conductive fabric for sensing device manufacturing to consider also these three parameters that determine the electrical performance.

Thickness

The substrate thickness is another critical parameter to consider in the design of antennas, sensors, and so on. The fabric thickness and the number of layers, along with the relative permittivity, determine the bandwidth, the gain and the efficiency performance of the corresponding planar antenna or resonator.

Textile materials are generally limited to a narrow range of relative permittivity. Therefore, the fabric thickness becomes more decisive when trying to maximize or minimize the bandwidth. This is explained by the relation with quality factor, Q, according to Equation (9).

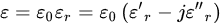
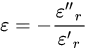
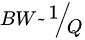
where the Q-factor results of the reciprocal relation of losses are shown in Equation (10): space wave (Q_rad) losses, conduction ohmic (Q_c) losses, surface waves (Q_s) losses and dielectric (Q_d) losses.

Therefore, the relation with the thickness of the substrate has to do with these losses individually: one characteristic of thin substrates is having elevated space wave losses (also known as ‘radiation losses’). This means that the thicker the fabric, the smaller the overall Q-factor (Q_t). Consequently, a larger bandwidth is allowed for a thicker substrate ^[23].

Flexibility, Elasticity and Mechanical Deformations

Textiles are key given their excellent flexibility and elasticity that allows their perfect adjustment in curved surfaces, as they can bend, elongate and compress. However, these properties may also be a disadvantage, as they lead to inaccurate measurements and dimensions when designing resonators and other electrical components. Also, it is found in the literature that modifying the shape of the sample does also imply a change in the resonance frequency of the device.

Not only this but the fact of bending has also a direct impact on the electrical properties, particularly the bandwidth, since the substrate thickness becomes irregular. This is an important parameter to measure when intending to use the device for human body applications. Here, the weave structure plays an important role as it might enhance the tensile strength.

2.2.2. Textile Substrates

Several articles are found in the literature investigating the RF applications (mainly the design of antennas and resonators) on fabric substrates. One of the most commonly used materials is felt, but there are others like goch, leather, jeans, cotton, silk, wax or even a combination of those ^[13].

Textiles’ dielectric properties are fully dependent on the dielectric behavior of their fibers, which are generally constituted by polymers. This explains why the relative permittivity of fabrics is so low compared to conventional electronics-related materials in the view of the fact that polymers are largely treated as insulators due to their low electrical conductivity ^[24].

The dielectric properties of some typical fabrics are listed in Table 4.

Table 4. Comparison of different materials characterized using ring resonator and patch antenna methods.

Ref.	Fabric	ε_r	tanδ	Frequency (GHz)
^[25]^[26]	Felt	1.22–1.38	0.0160–0.0230	2.45
^[25]	Cordura^®	1.90	0.0098	2.45
^[25]	Cotton ¹	1.60 ¹	0.0400 ¹	2.45
^[25]	100% Polyester	1.90	0.0045	2.45
^[27]	Viscose	1.64	0.0160	2.45
^[25]	Lycra	1.68	0.0080	2.45
^[25]	Quartzel^® Fabric	1.95	0.0004	2.45
^[25]	Cordura/Lycra^®	1.50	0.0093	2.45
^[25]	Tween	1.69	0.0084	2.45
^[25]	Panama	2.12	0.0500	2.45
^[25]^[27]	Jeans	1.62–1.70	0.0180–0.0250	2.45
^[25]	Moleskin	1.45	0.0500	2.45
^[27]	Fleece	1.20	0.0040	2.40
^[27]	Felt	1.36	0.0160	2.40
^[27]	Silk	1.20	0.0250	2.40
^[27]	Leather	2.95	0.1600	2.40
^[27]	Neoprene rubber	5.20	0.0250	2.40
^[27]	Cotton	1.54	0.058	2.40
^[27]	Polystyrene foam	1.02	0.00009	2.40
^[27]	Velcro	1.34	0.0060	2.40 & 5.00
^[27]	Denim	1.80	0.0700	2.40 & 5.00
^[27]	Tween	1.69	0.0084	2.60–3.95
^[27]	Silk	1.75	0.0120	2.60–3.95
^[26]	Polyester plain weave	3.20–3.66	0.018–0.0320	1.00
^[26]	Flax	4.22–6.20	0.0370–0.058	1.00
^[26]	Jute	2.99–4.95	0.0310–0.0470	1.00
^[26]	Hemp	4.08–4.77	0.0280–0.0520	1.00
^[26]	Wool	4.11–5.70	0.0280–0.0520	1.00
^[28]	100% Nylon 6.6	2.82–2.78	0.0268–0.0283	9.80
^[28]	Denim	1.70	0.085	2.22–2.59

¹ More detailed table in ^[26].

2.2.3. Conductive Fibers and Yarns

The factors that determine the performance of fabrics are, principally, the nature of the fibers, the yarn, the structure of the weave, the density of the thread, the air volume and the surface treatment, if any ^[29]. However, fabrics are susceptible to environmental conditions such as pressure, humidity, and temperature.

Fabrics are naturally insulating materials made of fibers. It is possible, though, to combine them with metallic fibers, filaments or coatings, or even with conductive polymers, so they become what is known as conductive fabrics or electro textiles. The first reference to this concept found in the literature was in 1952 by S.P. Hersh ^[30].

Dielectric fabrics are characterized for their really small or negligible conductivity. These are used in electronics as the dielectric substrate for the design of wearable and flexible devices, e.g., sensors, antennas or resonators. Here, the dielectric properties of the textile do truly determine their gain and efficiency.

Conductive Fibers

Conductive fibers can have a metallic, carbonic or polymeric nature. Their properties are enumerated in Table 5.

Table 5. Fiber categories, properties and their main applications ^[31]^[32]^[33].

Fiber Category	Material	Properties
Metal fibers	Stainless steel Silver Copper Aluminum Nickel Many alloys	High conductivity (≈105 S/cm) High mechanical and thermal strength Heat and corrosion resistant Anti-static properties Electromagnetic shielding
Carbon fibers	Polyacrylonitrile (PAN) Pitch Viscose Carbon black Graphene	High conductivity (≈104 S/cm) High mechanical strength Large specific surface area Low mass density Excellent mechanical properties Abrasion and wear resistance Anti-static properties are possible also
Conducting polymers	Polyaniline (PANI) Polypyrrole (pPy) Polystyrene sulfonate (PEDOT: PSS) Polythiophene (PT)	Excellent flexibility Low conductivity (the non-ionic polymers only) Poor mechanical properties Good electronic properties: high areal capacitance and areal energy density

Conductive Yarns

Conductive yarns are manufactured using purely metallic wires or they are simply core-covered by metal (usually stainless steel) having a conductivity range from 5 Ω/m to more than a few kΩ/m ^[34]. The classification found in the literature ^[35] is listed below.

Metallic filament yarns (metallic or metallized yarns);
Conductive hybrid yarns;
- Conductive composite yarns or metal composite embroidery yarns (MCEYs);
  
  ▪
  
  Core spun yarns;
  
  ▪
  
  Commingled yarns;
  
  ▪
  
  Blended spun yarns;
- Bi/multi-component spun yarns;
Inherently conductive polymer yarns (ICP);
Laminated/coated conductive yarns;
New conductive material and nanomaterial yarns.

The selection of the conductive yarn depends on the desired application, provided that each material has a specific conductivity level. Table 6 summarizes the possible applications for each yarn category.

Table 6. Yarn categories and their main applications ^[36].

Yarn Category	Applications
Metallic	Fabric-based circuits Core of composite yarns Heating fabrics Antimicrobial textiles Antipiercing gloves Anti0static
Conductive composite (MCEYs)	Antistatic and electromagnetic shielding Antibacterial Strain sensor
ICP yarns	Electromagnetic shielding Simple circuit Supercapacitor
Plated, laminated and coated	Supercapacitor Strain sensor
New conductive and nanomaterial	Microelectrode Antibacterial Antimicrobial textiles

2.3. Manufacturing Techniques

2.3.1. Etching

Etching is a chemical process whose basic principle is to engrave the desired pattern into a substrate by causing a corrosive effect between the photoresist masks and the etchants. In other words, the materials are removed from the board with liquid chemicals. This technique began in the 1960s, and it is also known as chemical etching or liquid etching ^[37]. Etching allows the manufacture of complex patterms with a high level of accuracy compared to other technologies.

2.3.2. Soldering and Welding

Both soldering and welding are joining techniques. These are widely used in flexible textile electronics to connect components and connectors to the conductive textile substrates (threads, flexible copper wires, polymides) ^[38].

In soldering, a filler metal (or solder) is melted to join two contacts. This third metal must have a lower melting temperature than the conductive thread or fabric. The conventional soldering technique requires high temperatures (above 200 °C), whereas lower temperatures (150 °C) are enough and required when working with fabric. However, not all conductive threads are suitable for soldering, for instance, stainless steel. The solder is a soft alloy of lead (Pb), tin (Sn) or silver (Ag) ^[39]. Some examples of the soldering technique applied to smart textiles is the integration of LEDs to the textile substrate using soldering conductive yarns ^[40].

Welding, similar to soldering, requires high temperatures to melt in this case both the metal and the textiles so they can be joined. This technique is seldom employed for e-textiles manufacture given the temperature conditions that limit the appropriate materials to use. The three main categories ^[41] are outlined below:

Resistance welding: This requires two metallic parts to be joined by applying an electrical current through them.
Ultrasonic welding: The ultrasonic acoustic vibrations with frequencies between 20 and 40 kHz generate heat and pressure that end up welding the two parts ^[42]. This is the most popular welding process with applications in multiple areas such as automotive, aerospace and health. An example is ^[43], where rotating ultrasonic welding technology is employed to integrate highly conductive ribbons into textile-based conductive tracks.
Radio-frequency (RF) welding: The RF absorbing polymer tape is positioned in the middle of the two fabric pieces, which melts by submitting to RF energy. This technique is of interest for non-weldable fabric materials.

2.3.3. Adhesive Conductive Foil

Conductive adhesive is commonly used in the shape of a sheet or strip especially for prototyping due to its low cost and easiness of employment. Adhesive copper tapes can be stuck or glued to many surfaces, e.g., ceramic cylinders ^[44], copper-clad substrates ^[45] or even textiles ^[13]^[46].

Copper foil tapes are commercialized in rolls and sheets of many dimensions and thicknesses. It is a remarkably modest material provided that the manufacturing process can be as elementary as cutting the strips manually with scissors to drawing the layout using a dedicated software and after printing and cutting it with a draft cutter.

The results, though, may not be indicated for purposes others than protoyping and pretesting or academic when it comes to employing this technique onto textiles because of their low reliability due to a lack of adherence over time (which impacts the sensing accuracy) compared to other technologies such as printing or embroidery.

2.3.4. Printing Technologies

A wide range of technologies can be employed for printing electronic components. These are advantageous for their lightness, low profile and low cost compared to the conventional technologies, e.g., etching ^[47].

The printing processes can be divided in two categories ^[48]:

Conventional printing: These are printing technologies that require a master (printing plate), which is basically the tool that enables the ink transfer to the printing substrate. The conventional printing processes are outlined below:
- Screen printing;
- Letterpress/flexography;
- Lithography/offset;
- Gravure printing.
Non-impact printing: These are masterless printing technologies (also known as ‘non-contact printing’ processes). These technologies employ laser to transmit the information to the intermediate carrier that will afterwards transfer it to the final substrate. The non-impact printing processes are outlined below:
- Electrophotography;
- Inkjet printing;
- Ionography;
- Magnetography;
- Thermography;
- Photography.

The application will determine in the vast majority of cases which is the most suitable printing technique. Generally, the minimum dot (feature) size and the throughput are the two main parameters to check against. However, others may also be taken into consideration ^[49].

Out of all the list enumerated above, screen-printing and inkjet-printing technologies have become the most relevant processes in the design of sensors and other electronic devices.

Screen Printing

Screen printing consists of the usage of a squeegee to apply pressure to the ink paste over a screen stencil, which is placed on top of the substrate. The stencil acts as a mask, meaning that the ink is imprinted through the non-covered cavities.

This technology is widely employed in electronics due to the good compatibility of materials, the low cost and the easiness of manufacturing ^[45]. However, the need to use a mask introduced an additional expense and material waste that may not be convenient when rapid prototyping ^[50]^[51].

Many applications are found in the literature for the design of RF antennas ^[52], RFID ^[53], smart packaging ^[54], plant biomarkers measurement ^[55], nitrate detection in water ^[56], monitoring metal pollutants ^[57], other smart wearables ^[58], IoT applications ^[59] and even electroluminescent matrix displays ^[60].

Inkjet Printing

Inkjet-printing technology is a contactless alternative widely employed for R&D and some other specific applications which involve the fabrication of latches ^[48]. It can either work with liquid or hot-melt ink. The functioning consists of the deflection of charged ink droplets by electric fields, which draws the desired image controlled electronically ^[47].

This technology has many variants—continuous ink jet, thermal (bubble) ink jet, piezo ink jet—that are used in accordance with the drop diameter and frequency.

In the literature, many applications are found for printed electronics, such as printed circuits, transistors, and amplifiers, in the design of antennas, sensors, RFID and audio devices. Many flexible color displays have also been developed so far using this technology ^[48]. Also, in the field of microwave technology, a recent (2020) study ^[61] has proven the feasibility of integrating circuits into microfluidic systems for heating and sensing purposes.

Comparing Screen Printing and Inkjet Printing

Screen- and inkjet-printing techniques are the most effective options in the field of printed electronics. While screen printing requires a stencil or master, it is still the best choice for mass production given the price–scalability compromise. On the other hand, inkjet printing is more recommended for prototyping and testing as long as it does not require a master ^[49].

In terms of the quality of the textile print, an experimental study ^[62] discloses the pigmentation outcomes of each technique on non-treated and pre-treated cotton fabrics.

The results show that inkjet-printed samples have an ink density three times lower than screen-printing ones, meaning that multiple passes are needed to obtain the same. Despite that, the color saturation is not affected by this factor but rather by the fabric properties, returning higher values for pre-treated cotton samples in general but still lower when using inkjet ink due to their viscosity and surface tension.

Between the four primary ink colors (magenta, cyan, yellow, black), many differences are also found that relate the viscosity with the density on each fabric.

2.3.5. Three-Dimensional (3D) Printing

With a wide range of commercially accessible printing methods and materials, additive 3D printing techniques have recently gained appeal, especially for the development of flexible antennas, mainly because of the wide range of materials that can be employed under the classification of polymers and resins, metals and ceramics.

Additive Manufacturing (AM) by 3D printing is attracting the attention of the scientific collective given the flexibility, cost-effective, simple and fast prototyping alternatives that it brings. The basic principle of this technology is the addition of subsequent layers of materials in the desired digital design until reaching the desired tridimensional figure. In this way, the width of the 3D-printed substrate will depend directly on the material used and on the number of stacked layers. Multiple AM techniques exist; the more common are listed below ^[63]^[64]:

Fused Filament Fabrication (FFF) or Fused Deposition Modeling (FDM);
Stereolithography (SLS);
Digital Light Processing (DLP);
Material Jetting (MJ).

Fused Deposition Modeling (FDM) is the most popular technique, which encompasses the high-temperature extrusion of the filament modeling the object from bottom to top. In the literature, several studies provide successful results of implementing FFF technology for the design of RFID antennas ^[65]^[66]^[67], broadband 5G on-package antennas ^[68], SRRs ^[69]^[70], microstrip resonators ^[71], dielectric resonator reflectarrays ^[72], and others.

2.3.6. Embroidery

Embroidery has become one of the most commonly used manufacturing techniques in the field of smart textiles, as it has been extended to multiple applications in aerospace engineering, construction, automotive, medicine and biomedical, amongst others ^[73]. This technique comprises the application of conductive yarn materials in a patterned design into a textile substrate.

Standard embroidery (or two-thread system) is the regular system generally employed to apply onto the textile a combined fine metal wire along with the yarns ^[74]. The Tailored Fiber Placement (TFP, also known as the ‘three-thread system’) dates back to the 1990s ^[75] and is an automated process that allows total control over the orientation and the directionality of the fibers in a composite preform. Using this technique, it is possible to build tridimensional structures of many shapes. The TFP method is recommended for glass or carbon fiber threads which are rigid and thick ^[76].

2.3.7. Weaving and Knitting

Weaving and knitting are two textile fabrication methods which allow the fabrication of 2D and 3D fabric structures by working with multiple warp and weft layers. The knitting process comprises the positioning of the yarns on a knitting needle defining consecutive loops or stitches that are connected either horizontally (weft) or vertically (warp) ^[77]. In the weaving process, the yarns are interlaced perpendicularly, which simplifies the exercise to insert the conductive yarn.

Weaving and knitting are recommended techniques especially when the desire textile surface’s dimensions are huge. The most remarkable properties of woven and knitted fabrics are outlined below:

Lightweight;
Portability;
Skin comfort;
Durability;
Deformation resistance (woven fabrics);
Elasticity and stretchability, air permeability, thermal retention (knitted fabrics).

2.3.8. Comparison of Wearable Electronics Integration Techniques

Table 7 summarizes all the aforementioned techniques. Figure 6 illustrates some application cases of resonator design employing them.

Figure 6. Some examples of wearable electronics manufacturing techniques: (a) Wet Etching: flexible split-ring resonator metamaterial structure fabricated on a polypropylene film by chemical etching ^[78]; (b) Welding and Soldering: components surface-mounted soldered to conductive fabric. Reproduced with permission. Copyright Liza Stark (http://thesoftcircuiteer.net/); (c1,c2) Adhesive Conductive Foil: implementation of (c1) a ring resonator and (c2) a stub resonator on textiles using adhesive copper tape ^[13]; (d1,d2) Screen Printing: (d1) an illustration of a conventional screen-printing process; (d2) prototype of 60 GHz flexible meta surface made of a unit cell of circular metallic rings embedded with a square-shaped ring and printed on Melinex ^[79]; (e) Inkjet Printing: split-ring resonator fabricated using an ink-jet printer using ink with silver nanoparticles ^[61]; (f) 3D Printing: chipless RFID tag made of rectangular slot ring tags, different IDs (left to right): ‘1111111111110’ and ‘1010101010100’ ^[80]; (g1,g2) Embroidery: (g1) embroidery methods (from left to right): standard embroidery and TFP ^[76]; (g2) embroidered transmission line loaded with a split-ring resonator on felt substrate with a satin pattern (60% density) ^[81]; (h1,h2) Weaving and Knitting: (h1) different knitted plain structure-based sensors and (h2) illustrated simulation of plain knit structure composed of conductive yarn and non-conductive yarn made from 100% polyester ^[77].

Table 7. Summary of the main advantages and challenges of the most common wearable electronics integration techniques.

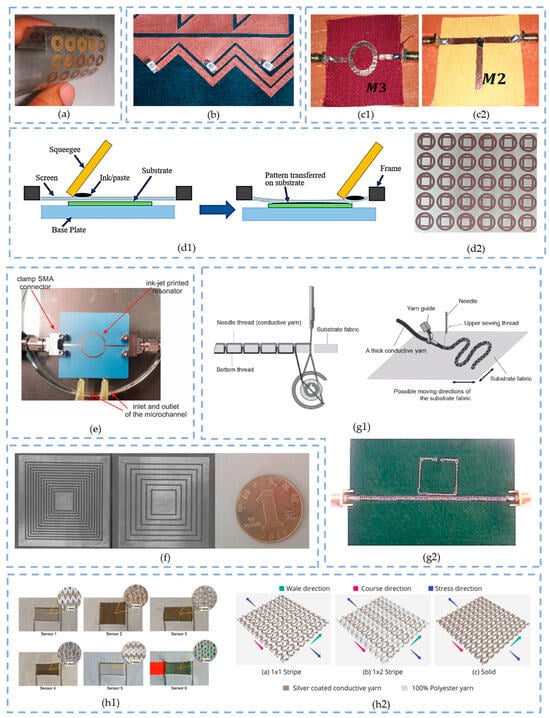
Technique	Advantages	Limitations
Wet Etching	Controllable etching rate Complex designs High resolution	Chemical contamination Depends on orientation Undercutting Not for small batch production Influenced by temperature and concentration of etchant High costs
Soldering and Welding	Low contact resistance Easy manufacture Efficient mass production Low cost Compatible with standard electronics processes Ultrasonic welding: not contaminant, biocompatible	Mechanically fragile Requires reinforcing when bending or stretching (not flexible at all) Requires high temperature Limited materials
Adhesive Conductive Foil	Low cost In-house made Flexible Good for prototyping Low curing temperatures Environmentally friendly	Disengages easily Low accuracy Not suitable for complex designs Fragile, easy to break Poor resolution High contact resistance
Inkjet Printing	No printed form is needed Ideal for prototyping High-quality prints Small losses	Limited colors Elevated cost of inks Poor print quality Slow print
Screen Printing	Price competing Good ink processability Efficient mass production Applicable to a final product Very flexible and stretchable Ideal for simple design	Printed form is required Long set up time Limited layer thickness Not efficient for prototyping or small batch production Huge waste of water Not possible in-house
3D Printing	In-house made Fully digital Fast fabrication Flexibility in materials Complex shapes and structures Adaptable density Lightweight	Difficult scalability High cost of AM manufactured material per weight Inconsistent quality Lossy materials Thermal instability Bending difficulties Poor resolution
Embroidery	2D and 3D structures Freedom of fibers orientation Good for prototyping Reduced waste Stable textile structures Very flexible and stretchable Precise and digitized (CAD) Variety of materials Scalability, mass production	Low precision in complex designs Difficult to automate Requires sealing to avert electrical shorting Slow process Performance impacted when bending or washing
Weaving and Knitting	Highly automated Stable textile structures Robust textile structures	Requires sealing to avert electrical shorting Fragile, easy to break Limited choice of yarns Performance impacted when bending or washing

This entry is adapted from the peer-reviewed paper 10.3390/s23229103

References

Hong, J.; Lancaster, M.J. Microstrip Filters for RF/Microwave Applications, 1st ed.; Wiley: Hoboken, NJ, USA, 2001.
Pozar, D.M. Microwave Engineering, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012.
Deng, Y.; Mengxia, Y.; Shi, Z. Design of Compact Dual-Mode Dual-Band Bandpass Filter for WLAN Communication System. Available online: https://link.springer.com/chapter/10.1007/978-3-642-21765-4_98 (accessed on 16 October 2023).
Mason, W.P.; Sykes, R.A. The use of coaxial and balanced transmission lines in filters and wide-band transformers for high radio frequencies. Bell Syst. Tech. J. 1937, 16, 275–302.
Baena, J.D.; Bonache, J.; Martin, F.; Sillero, R.M.; Falcone, F.; Lopetegi, T.; Laso, M.A.G.; Garcia-Garcia, J.; Gil, I.; Portillo, M.F.; et al. Equivalent-circuit models for split-ring resonators and complementary split-ring resonators coupled to planar transmission lines. IEEE Trans. Microw. Theory Tech. 2005, 53, 1451–1461.
Crabb, R.L.; Treble, F.C. Thin Silicon Solar Cells for Large Flexible Arrays. Nature 1967, 213, 1223–1224.
Cheng, I.-C.; Wagner, S. Overview of Flexible Electronics Technology. In Flexible Electronics; Wong, W.S., Salleo, A., Eds.; Electronic Materials: Science & Technology; Springer: Boston, MA, USA, 2009; Volume 11, pp. 1–28.
Zhou, Z.; Zhang, H.; Liu, J.; Huang, W. Flexible electronics from intrinsically soft materials. Giant 2021, 6, 100051.
Thin Silicon Solar Cells for Large Flexible Arrays|Nature. Available online: https://www.nature.com/articles/2131223a0 (accessed on 16 October 2023).
Overview of Flexible Electronics Technology|SpringerLink. Available online: https://link.springer.com/chapter/10.1007/978-0-387-74363-9_1 (accessed on 16 October 2023).
Cochrane, C.; Hertleer, C.; Schwarz-Pfeiffer, A. 2-Smart textiles in health: An overview. In Smart Textiles and Their Applications; Koncar, V., Ed.; Woodhead Publishing Series in Textiles; Woodhead Publishing: Oxford, UK, 2016; pp. 9–32.
ISO/TR 23383:2020; Textiles and Textile Products—Smart (Intelligent) Textiles—Definitions, Categorisation, Applications and Standardization Needs. ISO: Vernier, Switzerland, 2020.
Abolade, J.O.; Konditi, D.B.O.; Dharmadhikary, V.M. Comparative study of textile material characterization techniques for wearable antennas. Results Mater. 2021, 9, 100168.
Rhines, F.N. Microstructure-property relationships in materials. Metall. Trans. A 1977, 8, 127–133.
GB 9994-2008 English PDF (GB9994-2008). Available online: https://www.chinesestandard.net/PDF/English.aspx/GB9994-2008 (accessed on 16 October 2023).
Xie, Y.; Hill, C.A.S.; Jalaludin, Z.; Curling, S.F.; Anandjiwala, R.D.; Norton, A.J.; Newman, G. The dynamic water vapour sorption behaviour of natural fibres and kinetic analysis using the parallel exponential kinetics model. J. Mater. Sci. 2011, 46, 479–489.
Beckman, I.; Lozano, C.; Freeman, E.; Riveros, G. Fiber Selection for Reinforced Additive Manufacturing. Polymers 2021, 13, 2231.
Iqbal, M.; Sohail, M.; Ahmed, A.; Ahmed, K.; Moiz, A.; Ahmed, K. Textile Environmental Conditioning: Effect of Relative Humidity Variation on the Tensile Properties of Different Fabrics. J. Anal. Sci. Methods Instrum. 2012, 2, 92–97.
Fernández, D.P.; Mulev, Y.; Goodwin, A.R.H.; Sengers, J.M.H.L. A Database for the Static Dielectric Constant of Water and Steam. J. Phys. Chem. Ref. Data 1995, 24, 33–70.
Hertleer, C.; Van Laere, A.; Rogier, H.; Van Langenhove, L. Influence of Relative Humidity on Textile Antenna Performance. Text. Res. J. 2010, 80, 177–183.
Maryniak, W.; Uehara, T.; Noras, M. Surface Resistivity and Surface Resistance Measurements Using a Concentric Ring Probe Technique. Trek Appl. Note 2003, 1005, 1–4.
Sharaf, S.M. Chapter 7-Smart conductive textile. In Advances in Functional and Protective Textiles; ul-Islam, S., Butola, B.S., Eds.; The Textile Institute Book Series; Woodhead Publishing: Oxford, UK, 2020; pp. 141–167.
Salvado, R.; Loss, C.; Gonçalves, R.; Pinho, P. Textile Materials for the Design of Wearable Antennas: A Survey. Sensors 2012, 12, 15841–15857.
Bal, K.; Kothari, V. Measurement of Dielectric Properties of Textile Materials and Their Applications. June 2009. Available online: https://www.semanticscholar.org/paper/Measurement-of-dielectric-properties-of-textile-and-Bal-Kothari/c44cd84315748899af88b2e504e34f05f9294644 (accessed on 16 October 2023).
Singh, V. A Review of Textile Materials for Wearable Antenna. Nal Microw. Eng. Technol. 2014, 1, 7–14.
Yamada, Y. Dielectric Properties of Textile Materials: Analytical Approximations and Experimental Measurements—A Review. Textiles 2022, 2, 50–80.
Tsolis, A.; Whittow, W.G.; Alexandridis, A.A.; Vardaxoglou, J.C. Embroidery and Related Manufacturing Techniques for Wearable Antennas: Challenges and Opportunities. Electronics 2014, 3, 314–338.
Loss, C.; Gonçalves, R.; Pinho, P.; Salvado, R. A Review of Methods for the Electromagnetic Characterization of Textile Materials for the Development of Wearable Antennas. In Wireless Power Transmission for Sustainable Electronics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2020; pp. 27–56.
Thomas, L. 7-Woven structures and their impact on the function and performance of smart clothing. In Smart Clothes and Wearable Technology; McCann, J., Bryson, D., Eds.; Woodhead Publishing Series in Textiles; Woodhead Publishing: Oxford, UK, 2009; pp. 131–155.
Hersh, S.P.; Montgomery, D.J. Electrical Resistance Measurements on Fibers and Fiber Assemblies. Text. Res. J. 1952, 22, 805–818.
Zhang, Y.; Wang, H.; Lu, H.; Li, S.; Zhang, Y. Electronic fibers and textiles: Recent progress and perspective. iScience 2021, 24, 102716.
Li, X.; Chen, S.; Peng, Y.; Zheng, Z.; Li, J.; Zhong, F. Materials, Preparation Strategies, and Wearable Sensor Applications of Conductive Fibers: A Review. Sensors 2022, 22, 3028.
Tyler, D.J. Joining of wearable electronic components. In Joining Textiles; Elsevier: Amsterdam, The Netherlands, 2013; pp. 507–535.
McKnight, M.; Agcayazi, T.; Ghosh, T.; Bozkurt, A. Fiber-Based Sensors. In Wearable Technology in Medicine and Health Care; Elsevier: Amsterdam, The Netherlands, 2018; pp. 153–171.
Ismar, E.; Tao, X.; Rault, F.; Dassonville, F.; Cochrane, C. Towards Embroidered Circuit Board from Conductive Yarns for E-Textiles. IEEE Access 2020, 8, 155329–155336.
Raji, R.K.; Miao, X.; Boakye, A. Electrical Conductivity in Textile Fibers and Yarns—Review. AATCC J. Res. 2017, 4, 8–21.
Mann, R.P.; Nayak, A.P.; Islam, M.S.; Logeeswaran, V.J.; Bormashenko, E.; Wilson, K.A.; Vollmer, F. Wet Etching. In Encyclopedia of Nanotechnology; Bhushan, B., Ed.; Springer: Dordrecht, The Netherlands, 2012; pp. 2829–2830.
Stanley, J.; Hunt, J.A.; Kunovski, P.; Wei, Y. A review of connectors and joining technologies for electronic textiles. Eng. Rep. 2022, 4, e12491.
Simegnaw, A.A.; Malengier, B.; Rotich, G.; Tadesse, M.G.; Van Langenhove, L. Review on the Integration of Microelectronics for E-Textile. Materials 2021, 14, 5113.
Molla, M.T.I.; Goodman, S.; Schleif, N.; Berglund, M.E.; Zacharias, C.; Compton, C.; Dunne, L.E. Surface-mount manufacturing for e-textile circuits. In Proceedings of the 2017 ACM International Symposium on Wearable Computers, Maui, HI, USA, 11–15 September 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 18–25.
Locher, I.; Sefar, A.G. 10-Joining technologies for smart textiles. In Multidisciplinary Know-How for Smart-Textiles Developers; Kirstein, T., Ed.; Woodhead Publishing Series in Textiles; Woodhead Publishing: Oxford, UK, 2013; pp. 285–305.
Micus, S.; Rostami, S.G.; Haupt, M.; Gresser, G.T.; Meghrazi, M.A.; Eskandarian, L. Integrating Electronics to Textiles by Ultrasonic Welding for Cable-Driven Applications for Smart Textiles. Materials 2021, 14, 5735.
Dils, C.; Hohner, S.; Schneider-Ramelow, M. Use of Rotary Ultrasonic Plastic Welding as a Continuous Interconnection Technology for Large-Area e-Textiles. Textiles 2023, 3, 66–87.
Caizzone, S.; Buchner, G.; Elmarissi, W. Miniaturized Dielectric Resonator Antenna Array for GNSS Applications. Int. J. Antennas Propag. 2016, 2016, 2564087.
Andò, B.; Baglio, S.; Bulsara, A.; Emery, T.; Marletta, V.; Pistorio, A. Low-Cost Inkjet Printing Technology for the Rapid Prototyping of Transducers. Sensors 2017, 17, 748.
Roy, P.S.; Guha, M.; Roy, C.S. Wide band rectangular wearable microstrip ring antenna with textile substrate and its performance after washing. J. Phys. Conf. Ser. 2020, 1706, 012072.
Kipphan, H. (Ed.) Handbook of Print Media: Technologies and Production Methods; Springer: Berlin/Heidelberg, Germany, 2001.
Wiklund, J.; Karakoç, A.; Palko, T.; Yiğitler, H.; Ruttik, K.; Jäntti, R.; Paltakari, J. A Review on Printed Electronics: Fabrication Methods, Inks, Substrates, Applications and Environmental Impacts. J. Manuf. Mater. Process. 2021, 5, 89.
Huebner, G. Comparing Inkjet with Other Printing Processes and Mainly Screen Printing. In Handbook of Industrial Inkjet Printing; Zapka, W., Ed.; Wiley: Hoboken, NJ, USA, 2017; pp. 7–22.
Tu, H.; Hu, J.; Ding, X. Measurement of the Conductivity of Screen Printing Films at Microwave Frequency Employing Resonant Method. J. Electron. Mater. 2021, 50, 521–527.
Kazani, I.; Declercq, F.; Scarpello, M.L.; Hertleer, C.; Rogier, H.; Ginste, D.V.; Mey, G.D.; Guxho, G.; Langenhove, L.V. Performance Study of Screen-Printed Textile Antennas after Repeated Washing. Autex Res. J. 2014, 14, 47–54.
Xiao, G.G.; Zhang, Z.; Lang, S.; Tao, Y. Screen printing RF antennas. In Proceedings of the 2016 17th International Symposium on Antenna Technology and Applied Electromagnetics (ANTEM), Montreal, QC, Canada, 10–13 July 2016; pp. 1–2.
Hasni, U.; Piper, M.E.; Lundquist, J.; Topsakal, E. Screen-Printed Fabric Antennas for Wearable Applications. IEEE Open J. Antennas Propag. 2021, 2, 591–598.
Machiels, J.; Appeltans, R.; Bauer, D.K.; Segers, E.; Henckens, Z.; Van Rompaey, W.; Adons, D.; Peeters, R.; Geiβler, M.; Kuehnoel, K.; et al. Screen Printed Antennas on Fiber-Based Substrates for Sustainable HF RFID Assisted E-Fulfilment Smart Packaging. Materials 2021, 14, 5500.
Ruiz-Gonzalez, A.; Kempson, H.; Haseloff, J. A Simple Reversed Iontophoresis-Based Sensor to Enable In Vivo Multiplexed Measurement of Plant Biomarkers Using Screen-Printed Electrodes. Sensors 2023, 23, 780.
Inam, A.K.M.S.; Costa Angeli, M.A.; Shkodra, B.; Douaki, A.; Avancini, E.; Magagnin, L.; Petti, L.; Lugli, P. Flexible Screen-Printed Electrochemical Sensors Functionalized with Electrodeposited Copper for Nitrate Detection in Water. ACS Omega 2021, 6, 33523–33532.
Honeychurch, K.C.; Hart, J.P. Screen-printed electrochemical sensors for monitoring metal pollutants. TrAC Trends Anal. Chem. 2003, 22, 456–469.
Ibanez Labiano, I.; Arslan, D.; Ozden Yenigun, E.; Asadi, A.; Cebeci, H.; Alomainy, A. Screen Printing Carbon Nanotubes Textiles Antennas for Smart Wearables. Sensors 2021, 21, 4934.
Pan, K.; Fan, Y.; Leng, T.; Li, J.; Xin, Z.; Zhang, J.; Hao, L.; Gallop, J.; Novoselov, K.S.; Hu, Z. Sustainable production of highly conductive multilayer graphene ink for wireless connectivity and IoT applications. Nat. Commun. 2018, 9, 5197.
Ivanov, A. A Printed Electroluminescent Matrix Display: Implementation Details and Technical Solutions. In Proceedings of the 2018 IMAPS Nordic Conference on Microelectronics Packaging (NordPac), Oulu, Finland, 12–14 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 86–94.
Jasińska, L.; Szostak, K.; Kiliszkiewicz, M.; Słobodzian, P.; Malecha, K. Ink-jet printed ring resonator with integrated Microfluidic components. Circuit World 2020, 46, 301–306.
Kiatkamjornwong, S.; Putthimai, P.; Noguchi, H. Comparison of textile print quality between inkjet and screen printings. Surf. Coat. Int. Part B Coat. Trans. 2005, 88, 25–34.
Kirtania, S.G.; Elger, A.W.; Hasan, M.R.; Wisniewska, A.; Sekhar, K.; Karacolak, T.; Sekhar, P.K. Flexible Antennas: A Review. Micromachines 2020, 11, 847.
Chietera, F.P.; Colella, R.; Catarinucci, L. Dielectric Resonators Antennas Potential Unleashed by 3D Printing Technology: A Practical Application in the IoT Framework. Electronics 2021, 11, 64.
Kronberger, R.; Grunwald, S.; Wienstroer, V.; Tsatsos, V. New Low-Cost FDM Technology for Printing Antennas. In Proceedings of the 2020 International Symposium on Antennas and Propagation (ISAP), Osaka, Japan, 25–28 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 571–572.
Colella, R.; Catarinucci, L.; Michel, A.; Nepa, P. Design of a 3D-printed circularly polarized antenna for portable UHF RFID readers. In Proceedings of the 2017 IEEE International Conference on RFID Technology & Application (RFID-TA), Warsaw, Poland, 20–22 September 2017; pp. 225–228.
Rizwan, M.; Khan, M.W.A.; Sydänheimo, L.; Virkki, J.; Ukkonen, L. Flexible and Stretchable Brush-Painted Wearable Antenna on a Three-Dimensional (3-D) Printed Substrate. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 3108–3112.
Lin, T.-H.; Bahr, R.; Tentzeris, M.M.; Raj, P.M.; Sundaram, V.; Tummala, R. Novel 3D-/Inkjet-Printed Flexible On-package Antennas, Packaging Structures, and Modules for Broadband 5G Applications. In Proceedings of the 2018 IEEE 68th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 29 May–1 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 214–220.
Hamzah, H.; Lees, J.; Porch, A. Split ring resonator with optimised sensitivity for microfluidic sensing. Sens. Actuators Phys. 2018, 276, 1–10.
Salim, A.; Ghosh, S.; Lim, S. Low-Cost and Lightweight 3D-Printed Split-Ring Resonator for Chemical Sensing Applications. Sensors 2018, 18, 3049.
Javidmehr, S.; Maunder, A.M.; Daneshmand, M.; De Zanche, N. Toward Automated Manufacturing of RF Coils: Microstrip Resonators for 4.7 T Using 3D-Printed Dielectrics and Conductors. Appl. Magn. Reson. 2019, 50, 663–675.
Zhang, S. Three-dimensional printed millimetre wave dielectric resonator reflectarray. IET Microw. Antennas Propag. 2017, 11, 2005–2009.
Mecnika, V.; Hoerr, M.; Krievins, I.; Jockenhoevel, S.; Gries, T. Technical Embroidery for Smart Textiles: Review. Mater. Sci. Text. Cloth. Technol. 2014, 9, 56–63.
Eichhoff, J.; Hehl, A.; Jockenhoevel, S.; Gries, T. 7-Textile fabrication technologies for embedding electronic functions into fibres, yarns and fabrics. In Multidisciplinary Know-How for Smart-Textiles Developers; Kirstein, T., Ed.; Woodhead Publishing Series in Textiles; Woodhead Publishing: Oxford, UK, 2013; pp. 191–226.
Mattheij, P.; Gliesche, K.; Feltin, D. Tailored Fiber Placement-Mechanical Properties and Applications. J. Reinf. Plast. Compos. 1998, 17, 774–786.
Roh, J.-S. Conductive Yarn Embroidered Circuits for System on Textiles. In Wearable Technologies; Ortiz, J.H., Ed.; InTech: London, UK, 2018.
Rumon, M.A.A.; Cay, G.; Ravichandran, V.; Altekreeti, A.; Gitelson-Kahn, A.; Constant, N.; Solanki, D.; Mankodiya, K. Textile Knitted Stretch Sensors for Wearable Health Monitoring: Design and Performance Evaluation. Biosensors 2022, 13, 34.
Ragi, P.M.; Umadevi, K.S.; Nees, P.; Jose, J.; Keerthy, M.V.; Joseph, V.P. Flexible split-ring resonator metamaterial structure at microwave frequencies. Microw. Opt. Technol. Lett. 2012, 54, 1415–1416.
Jilani, S.; Falade, O.; Wildsmith, T.; Reip, P.; Alomainy, A. A 60-GHz Ultra-Thin and Flexible Metasurface for Frequency-Selective Wireless Applications. Appl. Sci. 2019, 9, 945.
Ma, Z.; Jiang, Y. High-Density 3D Printable Chipless RFID Tag with Structure of Passive Slot Rings. Sensors 2019, 19, 2535.
Moradi, B.; Fernández-García, R.; Gil, I. Effect of smart textile metamaterials on electromagnetic performance for wireless body area network systems. Text. Res. J. 2019, 89, 2892–2899.

© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.