HNN modeling is the combination of artificial neural networks (ANNs) with prior knowledge in a mathematical framework. There are two main approaches to incorporating prior knowledge: design and training methods. Design approaches use prior knowledge to define the network structure, while training approaches use it to guide parameter estimation. Both approaches reduce data dependency, making models less sensitive to sparse and noisy data, and improving their descriptive and predictive capabilities compared to pure ANNs. HNNs are a powerful tool for understanding complex processes like bioprocesses and accelerating product development. Bioprocess modeling is challenging due to nonlinearity, dynamics, and uncertainty. Traditional models based on physical and chemical laws can be overly simplistic or hard to calibrate. Data-driven ANN models lack interpretability and generalization. HNNs combine the strengths of both approaches, enhancing the accuracy, robustness, and efficiency of bioprocess modeling by integrating prior knowledge with ANNs.
1. Introduction
Hybrid neural network (HNN) modeling may be defined as the combination of artificial neural networks (ANNs) with prior knowledge in a common mathematical structure. According to Thompson and Kramer
[1], there are two main approaches to embodying prior knowledge in neural network models, namely design and training approaches. In design approaches, prior knowledge dictates the structure of the model. Prior knowledge is used to define the ANN topology (e.g., number of layers, types of layers, types of nodes), for modularization of the network, or to include nonnetwork mathematical equations (e.g., physical laws) in tandem with the ANN model. In training approaches, the prior knowledge dictates the parameter estimation problem either in the form of variable constraints, network weights constraints, or the definition of the loss function. In both design and training approaches, the inclusion of prior knowledge reduces data dependency: in design approaches, the dimension of the parameter space is reduced (i.e., the ANN is smaller, and the number of weights is lower), whereas in training approaches, the feasible region of the parameter space is reduced. In both cases, the training becomes less sensitive to sparse and noisy data and the final model improves its descriptive and predictive power in relation to a fully ANN model.
2. Design Approaches
In design approaches, prior knowledge shapes the structure of the HNN model. Design approaches may be further subdivided into modular and semiparametric design. In modular design, the overall model is decoupled into smaller interconnected modules. A biochemical process typically comprehends several interconnected unit operations. Instead of a large ANN to describe the full process, smaller ANNs may be interconnected to match process topology (prior knowledge). Whereas in a single ANN, all input nodes are connected to all output nodes, in modular ANNs, the connectivity is sparser, the number of parameters is reduced, and the data requirements are therefore also reduced. The modular ANN model is also more transparent, as the input/outputs variables of the modules have physical meaning. The hierarchical neural network model proposed by Mavrovouniotis and Chang is an example of modular ANN design
[2]. A more recent example is the knowledge-based ANN concept proposed in
[3].
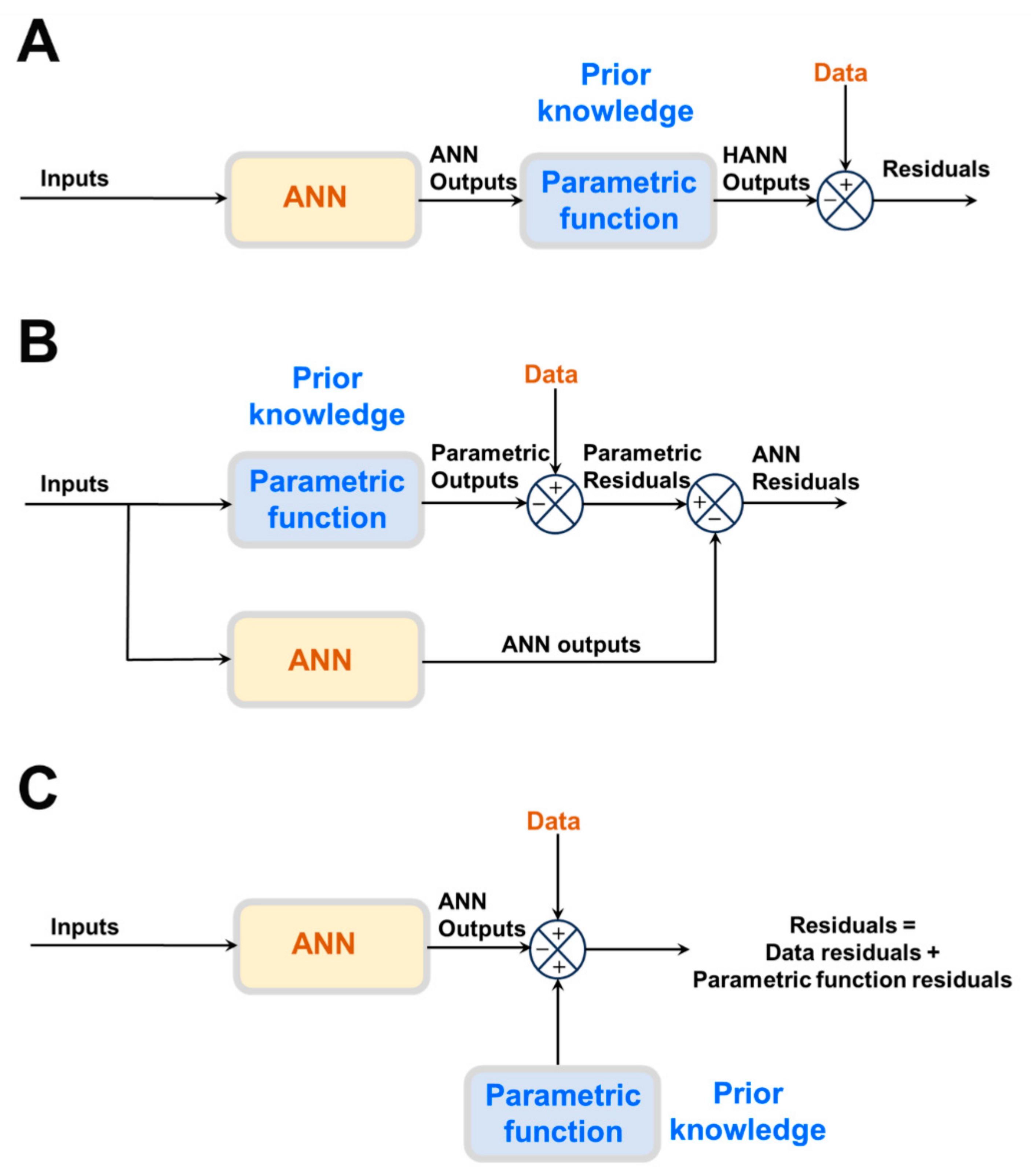
The most frequently reported approach is semiparametric design (Figure 1A,B), in which physical laws are directly incorporated in the model structure. Instead of a large ANN, a smaller one is combined with physical laws in the form of a semiparametric model. Semiparametric models combine per definition parametric and nonparametric functions in the same model structure. Parametric functions are derived from prior knowledge of first principles, well-established mechanisms, and/or empirical correlations. They have a fixed mathematical structure and a fixed number of parameters with physical interpretation. On the contrary, ANNs are nonparametric functions entirely derived from process data. They have a loose structure without physical interpretation. Both model components are trained together.
Figure 1. Different methods to embody prior knowledge in HNN models: (A) Serial semiparametric hybrid structure. (B) Parallel semiparametric hybrid structure. (C) Physics-informed neural network structure.
Semiparametric HNN models can be classified as serial or parallel (
Figure 1A,B). In serial structures (
Figure 1A), the parametric equations (prior knowledge) cover only some parts of the process. The ANN has the job of learning from data the cause–effect relationships of those process parts lacking prior knowledge. One example of a serial semiparametric structure is the Psichogios and Ungar bioreactor hybrid model
[4], where an FFNN (nonparametric model that calculates bioreaction kinetics) is connected in series with macroscopic material balance equations (parametric model). Other examples are the general bioreactor hybrid model
[5] and the neural ordinary differential equation (neural ODE) model
[6][7].
In the case of parallel semiparametric structures (
Figure 1B), a full parametric model stemming from prior knowledge exists that, however, is not sufficiently accurate to describe the process. The ANN runs in parallel to compensate for parametric model inaccuracies. The parametric model takes priority in describing the process outputs. Firstly, the parametric model parameters are estimated to minimize the model–process mismatch. Then, the residuals of the parametric model are calculated over the data input space. If the residuals contain relevant information beyond the noise level, an ANN is trained to extract the cause–effect relationship from the parametric model residuals. The size of the ANN compensator is inversely proportional to the explained data variance using the parametric model. In limit, if the explained variance is sufficiently high, then the ANN compensator is not needed. Conversely, if the explained variance is negative, then the parametric model should be removed since a fully ANN will perform better than the hybrid structure. Examples of parallel semiparametric hybrid models are provided by, e.g., Côté et al.
[8], Piron et al.
[9] and Peres et al.
[10]. The bioreactor model proposed by Thompson and Krameris simultaneously parallel and serial
[1]. The biological kinetics are described with a Monod-type kinetic model (parametric) connected in parallel with a RBFN (nonparametric) compensator. The RBFN performs an additive correction of the Monod-type kinetic model outputs. The corrected kinetics are then connected in series with macroscopic material balances (parametric) in a similar way to the model reported by Psichogios and Ungar
[4].
3. Training Approaches
Prior knowledge may also be incorporated in HNN models through the training method. It may dictate constraints on process variables, e.g., concentrations or reaction rates of irreversible reactions must be positive. Variable inequality constraints, network weights inequality constraints, and loss function regularizers may be introduced in the training method to enforce such desired output behavior
[1]. Several methods have been developed to enforce ANN output monotonicity, convexity, concavity, or smoothness by adding parameter constraints and loss function regularizers
[11][12]. More recently, physics-informed neural networks (PINNs) have emerged for modeling CFD problems based on the Navier–Stokes equations
[13] or partial differential equations (PDEs) in general. The innovative aspect of PINNs is that physical equations are embodied in a “pure” ANN structure via the training approach (
Figure 1C). PINNs use a DNN to parameterize state variables over independent variables (time and spatial coordinates). Automatic differentiation (AD) is applied to obtain partial derivatives of the state variables in time and spatial coordinates and to calculate a PDE’s agreement error (the terms on the right and left sides of the PDEs equations must agree with each other). Two different sets of residuals are simultaneously minimized during the training: (i) the measurement residuals between calculated and measured state variables; (ii) the Navier–Stokes PDEs agreement (physics) residuals. PINNs have been shown to converge to PDEs solutions obtained using numerical discretization methods. Moreover, PINNs have been shown to seamlessly integrate data and mathematical models in flow problems
[14]. A key advantage of PINNs in relation to semiparametric HNNs is that numerical integration, or any other numerical method inherent to the parametric model, are avoided. This may be a substantial advantage in the case of PDEs and stiff systems of ODEs. Possible disadvantages are, however, that the exact mapping of the physical laws to the DNN structure is not guaranteed and that the physical laws may not be obeyed in case of extrapolation.
4. General Bioreactor Hybrid Model
Since the pioneering works by Psichogios and Ungar
[4], Thompson and Kramer
[1], and Schubert et al.
[15][16], attempts were made to propose a bioreactor HNN structure that covers a wide range of problems
[5][17][18][19][20]. The general bioreactor hybrid model (
Figure 2) is a serial semiparametric structure that combines an ANN and a system of ODEs with information feedback. Prior knowledge is represented by a system of ODEs derived from macroscopic material balances and/or intracellular material balances. These may be divided into a state–space model and a measurement model that computes observable process outputs. The ANN is used to model cell properties (lacking fundamental knowledge) as a function of the process state and exogenous inputs. The observable outputs are compared with training examples under a supervised learning scheme.
Figure 2. General deep hybrid model for bioreactor systems. The model has parametric functions (functions f(.) and h(.)) with fixed mathematical structure; typically material/energy balance equations). Some process properties, v, lacking mechanistic explanation are modelled using a feedforward neural network (FFNN) as a function of the process state, x; exogenous inputs, u; and time, t. FFNN is a nonparametric function with loose structure that must be identified from process data given the absence of explanatory mechanisms for that particular part of the process. The model is dynamic in nature with state vector, x, and observable outputs, y, changing over time.
Most previous studies have adopted a shallow HNN configuration based on three-layers FFNNs (with a single hidden layer with tanh activation function) connected in series with material balance equations. Shallow HNNs are typically trained in a least squares sense employing the Levenberg–Marquardt optimization algorithm. The computation of gradients follows the indirect sensitivity method originally proposed by Psichogios and Ungar
[4] and detailed by Oliveira
[5]. Sensitivity equations are required because the observable outputs, y, are not directly linked to the ANN outputs, v. Cross-validation is adopted to prevent overfitting. Recently, the general bioreactor HNN has been extended to deep multilayered FFNNs and deep learning
[19][21][22]. Multiple hidden layers with rectified linear unit (ReLU) activation functions were adopted, connected in series with material balance equations. The ADAM algorithm
[23] was applied to train the deep HNN in a weighted least squares sense. The objective function gradients were computed using modified semidirect sensitivity equations, thereby significantly reducing the CPU time
[19]. Stochastic regularization based on random training examples and ANN weights dropout was adopted to mitigate overfitting. Deep HNN modeling was shown to systematically generalize better than shallow HNN modeling.
This entry is adapted from the peer-reviewed paper 10.3390/fermentation9100922