Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is an old version of this entry, which may differ significantly from the current revision.
Subjects:
Engineering, Aerospace
Continuous evolution in nature has created optimum solutions for creature survival that have inspired many innovative engineering designs. Riblet geometries, passive flow control devices, have been studied, which were inspired by the skin of fast-swimming sharks. Turbulent boundary layer research reveals the positive effect of riblets in reducing drag by manipulating turbulent structures.
- riblet design
- turbulent boundary layer
- drag and noise reduction
- aircraft
1. Introduction
From billions of years ago until now, continuous evolution in nature has provided high-performance, innovative solutions for the survival of creatures. During the history of science, different research studies have been conducted by imitating nature to make improvements in engineering decisions. The imitation of birds in realizing the long-held dream of humankind for flight is a well-known example of this argument. The emergence of flight was not a conventional replication of the structure of bird wings in detail but was imitated from other naturally evolved methods of birds flying. As an example, there are differences in methods for short- or long-range flying birds [1,2,3,4,5]. As nature has its own solutions for adapting to the environment, in today’s eco-friendly optimum engineering designs, imitating these naturally evolved and “optimum solutions” would potentially accelerate technology development and reduce engineering research costs [2,3,5,6].
On this basis, one of the researchers’ greatest challenges is finding the cause-and-effect relationship in nature to benefit from natural phenomena in the design of optimized devices. This would be more challenging when optimum results by nature are extracted after a multi-objective evolution, which is improved based on the creature’s habitat for different natural reasons [7]. The theory of silent flight is an example investigated by researchers to mimic the noise reduction abilities of owls’ wings [8,9,10,11,12,13]. Reducing far-field noise is an important parameter that evolved over the body and wing structure of this species. It is revealed that having large wings with low aspect ratios, serrations in the leading and trailing position of the wings, wavelet-like surfaces, and grooves over the feathers on lower parts of the wings would have a positive effect on reducing radiated noise. The optimum design of shark skin that has contact with water is another example that has evolved by nature. As a multi-objective evolutionary process, the anti-fouling and hydrophobic ability also evolved besides its reduction in drag. The idea of using shark skin structure on the surface that is in contact with the fluid flow is introduced as a solution to reduce frictional drag [14,15,16,17,18]. In this regard, many innovative surfaces replicated from shark skin made their way to the industry, facilitating improvements in engineering designs, especially in friction drag [19].
In aerodynamics, drag is a directional force that acts against movements between fluid and solid body. It always resists movements by producing two main types of resisting forces, named form drag, also known as pressure drag and skin friction drag. Form drag is the opposite force generated by air molecules when flowing past the solid body and pushing it harder against forward rather than backward motion [20]. Skin friction drag, or viscous drag, is the resisting force generated through the moving of fluid flow over the object’s surface. Flow viscosity and velocity are the main factors that act on the value of skin friction drag. In addition to the above-mentioned fluid property factors, roughness and surface area exposed to the flow would affect the friction drag value.
Riblets can be considered bio-inspired replications of fast-swimming sharks that acceptably mitigate friction or viscous drag through the surface [14,15,21,22]. These aligned to the flow micro-size geometries can potentially lift high energetic, turbulent vortices from the surface to the riblet tips, leading to less interaction between the surface and turbulent vortices, hence resulting in friction drag reduction [2,23,24,25,26]. Since riblet performance shows the possibility of drag reduction, several numerical and experimental activities have been conducted to investigate different sizes and configurations over these geometries. There is also a wide range of analyses, including simple extrusions as well as complex 3D geometries, combined with various other methods for reducing drag [26,27,28,29,30].
Moreover, riblets show promise for adaptation to various flow control applications for drag reduction, such as aviation, marine ships, automotive, wind energy, sports, and medical fields [1,2,3,17,31,32,33]. Since the first fundamental studies on riblets by the NASA Langley Research Centre in the 1970s [34], many studies have been conducted that show immense potential for drag reduction and greenhouse reduction by sharkskin-inspired riblets in aviation [18,29,35,36,37,38,39,40]. Szodurch estimated that riblets could lead to a 2% draft reduction by an Airbus 320 if 70% of the aircraft is covered with riblets. In 1987, the racing yacht “Stars and Stripes” with the implementation of riblets from NASA and 3M won the America’s Cup and the gold medal at Olympia [41]. In 2010, the BMW Oracle team won the 33rd America’s Cup with their racing yacht covered with riblets [42], In 2012, riblets found their applications on wind turbine blades [31] and a Formula 1 car by Bionic Surface technology [43]. Moreover, riblets’ antifouling properties have been studied for potential applications on marine ships, medical implants, water treatment systems, and food and beverage industries [44,45,46].
Despite the common underlying physics of riblets in drag reduction and other applications, translating riblet technology to different domains poses challenges related to scale, environmental conditions, and surface materials. As an example, in the field of wind energy, wind turbine blades require considerations of larger scales and dynamic load variations, while underwater vehicles involve hydrodynamic complexities. Ensuring the robustness and durability of riblet structures in diverse conditions, as well as addressing manufacturing and maintenance aspects, are key challenges when applying riblet technology [14].
2. Physics of Riblets
Multiple research studies have been undertaken to examine the effectiveness of various riblet geometries in reducing drag. The effectiveness of drag reduction is closely linked to the flow properties, size and configuration of riblets [23,26,30,62,63]. Some conventional shapes of riblet geometries are illustrated in Figure 1. Bladed [62], triangular [29], semi-circular [26,64], trapezoidal [51,65,66,67] and spaced triangular [68] are some of the most conventional geometries. Riblets drag reduction can be characterized by non-dimensional parameters, namely: (1) non-dimensional spacing, defined as 𝑠+=𝑠·𝑢𝜏/𝜈, in which ν is the kinematic viscosity and 𝑢𝜏 is the friction velocity known as a function of viscous shear stress ( ), and (2) non-dimensional height of the grooves (ℎ+). The non-dimensional parameters are generally used to compare the outcomes of using riblets with available numerical and experimental studies [6,22,50,65]. In addition, by utilizing experimental data from diverse riblet configurations, the square root of non-dimensional riblet cross-section area ( ) has been introduced [57]. The goal was to determine if it could be feasible to represent drag reduction through a geometric parameter capable of encompassing the combined impact of riblet spacing and shape. This approach was implemented as another effective parameter for the characterization of riblets [69,70].
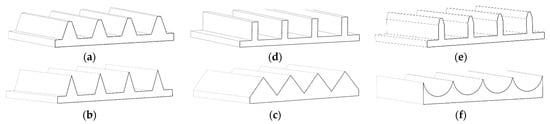
Figure 1. Conventional riblet geometries: (a) trapezoidal, (b) spaced triangular, (c) triangular, (d) bladed, (e) trapezoidal bladed, and (f) semi-circular.
Several researchers have dedicated their studies to investigating the effects of riblets on both boundary layers and free stream flows. Specifically, they have focused on examining the coherent structures present within the turbulent boundary layer, particularly in areas influenced by the wall. These coherent structures exhibit unique characteristics, including smaller sizes and complex three-dimensional fluctuations, which differ from the overall flow behavior [71]. These property fluctuations in the airflow over the surface of a commercial aircraft at an altitude of 12.2 km, with a Mach number (M) of 0.8 and a Reynolds number (Re) of 106 can be in the order of microns [32,50].
The coherent structures are a part of the process of sweep and ejection with momentum exchange inside the turbulent boundary layer [18,26,72]. Momentum exchange in the turbulent boundary layer would be accrued by approaching high-speed flows to the surface (known as sweep) that is associated with positive u-component and negative v-component velocities and moving the low-speed flows from the near wall to toward freestream flow (known as ejection) that is associated with negative u-component and positive v-component velocities; this would result in shear stress effects inside the turbulent boundary layer [18,73]. The process of sweep and ejection causes near-wall longitudinal vortices, which lead to small spanwise motions in the viscous sub-layer and then increased friction drag [73]. Riblets, like small longitudinal fences, can hamper the movements of these vortices in such a way as to control skin friction drag [32,35,74,75,76].
Research studies have been mainly focused on the viscous sublayer, the area with 𝑦+<5, given that 50% of turbulent energy is generated in the lower region (i.e., the lower 5% area) of the turbulent boundary layer [77]. To prevent the occurrence of sweep and injection between flow layers, riblet geometries with sizes comparable to the viscous sublayer are necessary. This size requirement ensures effective impedance of the flow interactions and promotes desired flow behavior [21]. A classical definition of drag reduction by riblet surfaces is defined by using the concept of surface-wetted area [21,78]. Compensation of the surface wetted area is an important factor in evaluating the drag reduction performance by riblets. In this context, the level of interaction between surface and fluid flow is an indication of the shear stress and friction drag [17]. In the riblet surfaces, turbulent flow is lifted up and interacts with riblet tips that decrease wetted area and fluid shear stress [79]. In comparison to the smooth surface, adjusting the flow vortices above the valleys of riblets results in lower values of cross-stream flow fluctuations and reduces turbulent kinetic energy near the surface [65,79,80]. Importantly, these adjustments also minimize pressure fluctuations in the outer layers of the flow. These alterations have the potential to influence the emitted sound in compressible fluids, especially in aviation-related contexts [51,65].
As the reduction in wetted area is the main concept behind drag reduction, the number of indentations per unit of length should be within an optimum range [21]. The effect of non-dimensional spacing, 𝑠+, in drag reduction for a triangular riblet geometry with peak sharpness of 60° is illustrated in Figure 2. The figure indicates the limit of drag reduction when riblets spacing tends to be zero. Drag reduction achieves its optimum values at about 𝑠+≈15. Increasing 𝑠+ further would result in decreased effectiveness, causing an increase in drag more than zero, which is defined in the figure as a rough surface [35].
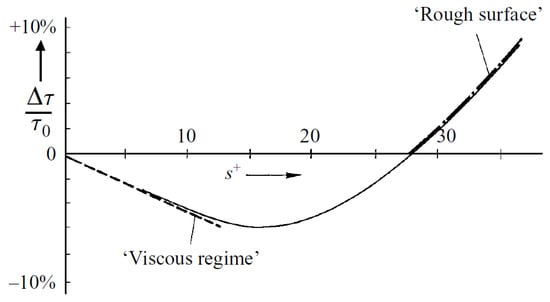
Figure 2. Effect of non-dimensional spacing in a drag reduction of a triangular riblet with 60° peak sharpness [55].
Research efforts have been dedicated to examining the aerodynamic implications of riblets on curved surfaces, particularly in the context of aircraft aerodynamics. Investigations have specifically targeted 3D applications to account for the complexities arising from variations in flow alignment experienced when airflow interacts with curved surfaces. To address these challenges, researchers have introduced curved riblet configurations featuring diverse riblet shapes, non-dimensional spacing and height. These design considerations aim to optimize drag reduction performance and effectively manage the intricate aerodynamic characteristics associated with curved surfaces [81].
Experimental and numerical studies have been conducted to investigate the impact of riblets on the structure of the boundary layer. To comprehensively understand riblet performance across different scales, a hierarchical analysis approach can be adopted. Starting at the micro-scale, detailed simulations and experiments delve into the fluid dynamics within individual riblet grooves and their interaction with the boundary layer, unveiling insights into local drag reduction mechanisms. Advancing to macro-scale, full-scale computational fluid dynamics simulations can evaluate the overall aerodynamic effect of riblets on complete aircraft systems, considering intricate flow interactions. In the experimental and numerical investigations, both viewpoints are considered separately or in a combined method. Generally speaking, these studies analyze the characteristics of the boundary layer before and after the application of riblets on flat and curved surfaces. The flow properties, including mean and fluctuating terms in the longitudinal, lateral, and vertical directions, are examined. The fluctuating terms not only influence the aerodynamic aspects but also have significant implications for the acoustical properties and generated noise [51,62].
Acknowledging the intersection of experimental and numerical research in exploring the impact of riblets on boundary layer structure, a comprehensive understanding of riblets’ performance across diverse scales can be achieved through a hierarchical analysis framework. This approach entails a progression from the micro-scale, where detailed simulations and experiments illustrate the fluid dynamics within individual riblet grooves and their interaction with the boundary layer, showing localized drag reduction mechanisms. Advancing to the macro-scale, extensive computational fluid dynamics simulations assess the aerodynamic influence of riblets on aircraft systems, encompassing intricate flow interactions. Broadly, these inquiries dissect the characteristics of the boundary layer in both pre and post-riblet application on both flat and curved surfaces. Flow properties, including mean and fluctuating components along the longitudinal, lateral, and vertical axes, undergo meticulous examination. Significantly, these fluctuating terms extend their influence beyond aerodynamics, affecting acoustical attributes and noise generation [51,62].
This entry is adapted from the peer-reviewed paper 10.3390/app131910893
This entry is offline, you can click here to edit this entry!
