Non Linear Current-Voltage Characteristics: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Md Tahmid Hussain
,
Mohd Tariq
,
Adil Sarwar
,
Shabana Urooj
,
Amal BaQais
,
Md. Alamgir Hossain

The current-voltage (IV) curve of a solar photovoltaic (PV) array provides valuable insights into its behavior under varying conditions, including partial shading. Under normal, unshaded conditions, the IV curve depicts a characteristic shape where the current increases linearly with voltage until it reaches a peak known as the maximum power point (MPP). 

  • solar PV
  • IV curve
  • PV power

1. Solar PV Array

A solar photovoltaic (PV) array is a collection of interconnected solar panels, each comprising multiple photovoltaic cells, designed to capture sunlight and convert it directly into electricity through the photovoltaic effect. These arrays are strategically configured to optimize solar exposure and energy capture, forming a functional unit capable of generating electrical power from the sun’s radiant energy. The power output is insignificant from a single PV cell. Ten multiple cells are connected in series to form a solar panel with a much higher voltage and power rating. The panels are further connected in a series or parallel fashion, which is shown in Figure 1, to obtain a higher voltage and current, thereby increasing the power rating required for the application. The number of panels can go up to thousands for large PV plants that can feed power to the grid. Solar PV arrays are used for various applications, ranging from small-scale residential installations to large-scale commercial and utility-level solar farms, contributing to the generation of clean and renewable energy [1].
Processes 11 02776 g001
Figure 1. Formation of Solar PV module from the series connection of solar PV cells.

2. Non Linear IV Characteristics

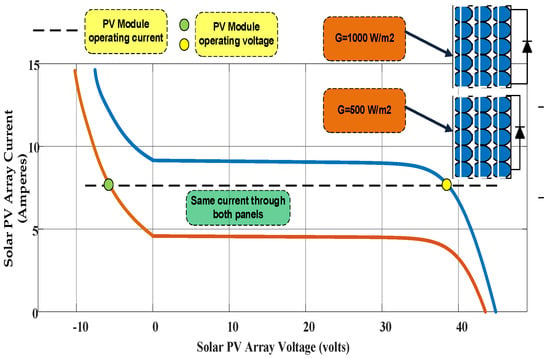
The major issue associated with solar PV output utilization is the nonlinear IV and PV characteristics of the solar PV panel [2]. Figure 2 and Figure 3 show, respectively, the current-versus-voltage and power-versus-voltage curve graph of a PV module during PSC. The reverse bias effect caused by PS on a two-module system is shown in Figure 2.
Processes 11 02776 g002
Figure 2. IV characteristic curve with PSC.
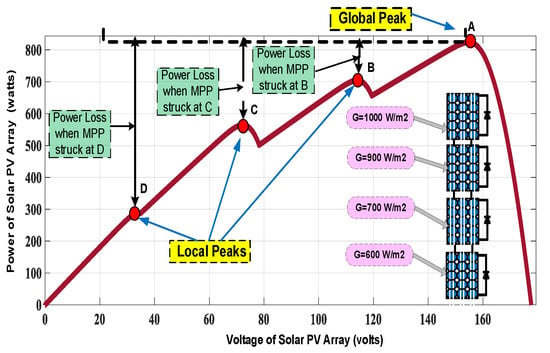
Processes 11 02776 g003
Figure 3. PV characteristics curve with PSC.
Figure 2 shows the two IV characteristic curves of a solar panel with partial shading of 1000 m/s2 and 500 m/s2. The IV characteristic shows how the current flows through the solar panel as the voltage increases. The blue line represents the IV curve at an irradiance value of 1000 m/s2, whereas the red line presents the IV curve at an irradiance value of 500 m/s2. The current is proportional to the voltage, up to a point. Beyond that point, the current starts to saturate and does not increase as much with increasing voltage. The saturation point is the point at which the solar panel produces the maximum amount of power, and the maximum power point is the point on the IV curve where the power is the greatest. The current output of the panel decreases as the level of shading increases, whereas the voltage output of the panel remains constant as the level of shading increases. Furthermore, the IV curve shifts to the right as the level of shading increases. This means that the panel requires a higher voltage to reach the same current output.
The breakdown voltage, also referred to as the reverse breakdown voltage, signifies the point at which a semiconductor device, such as a PV cell/module, experiences a sudden surge in current when reverse-biased. This phenomenon, often associated with ‘avalanche breakdown’ or ‘Zener breakdown’, emerges due to the intense electric field in the semiconductor depletion region, which results in the release of charge carriers through collision processes, leading to a rapid increase in current. Furthermore, bias voltage, encompassing both forward and reverse bias conditions, plays a pivotal role in the operation of PV cells/modules. When reverse bias is applied—by introducing a negative voltage to the cell’s terminals—it can unintentionally occur due to factors such as shading or night-time operation. It is paramount to recognize that this reverse-bias operation can trigger unintended adverse effects, including potential damage to the cell/module due to excessive current during the breakdown phase.
Figure 3 shows the IV characteristic curve of a solar panel with partial shading. The current-voltage (IV) curve of a solar PV array provides valuable insights into its behavior under varying conditions, including partial shading. Under normal, unshaded conditions, the IV curve depicts a characteristic shape where the current increases linearly with voltage until it reaches a peak known as the maximum power point (MPP). However, under partial shading, this curve can exhibit unique characteristics due to non-uniform illumination across the array, which can be seen in Figure 3.
When partial shading occurs on a PV array, the IV curve can exhibit multiple local MPPs. These are points where a shaded portion of the array operates at its peak power output considering its specific current-voltage relationship. Each shaded section of the array will have its own local MPP, and the overall power generation can be limited to the lowest of these local MPPs. This limitation arises because the shaded sections act as resistors, causing voltage drops and reducing the current flow. As a result, the local MPPs represent the optimal operating points for each shaded area, whereas the global MPP represents the point on the IV curve where the entire array operates at its maximum power output. It considers the collective effect of all shaded and unshaded sections of the array. Achieving the global MPP is a challenge under partial shading, as the voltage and current variations due to shading can push the system away from this optimal point. Strategies such as bypass diodes, shading analysis, and advanced MPPT algorithms aim to guide the system towards the global MPP by dynamically adjusting the current-voltage characteristics of the array. The PV module power output also decreases directly with shading. However, shading has no impact on the PV module efficiency or fill factor [3]. The maximum power available at a unique knee point needs to be tracked under insulated conditions. Solar panels connected in a series receive different irradiance due to shading from the passing clouds. This leads to a hotspot formation problem, which may lead to failure of the PV panel because of the rise in temperature of the shaded panel. The bypass diodes can mitigate the problem [4]. Bypass diodes are connected in parallel to each panel. The shaded panel is bypassed during shading, avoiding hotspot formation.
As a result, the MPPT becomes more difficult since conventional algorithms, including those focused on hill climbing, involve iteratively increasing or decreasing the input voltage or current until the MPP is reached. However, with nonlinear IV and PV characteristics, the MPP can be a local peak, and hill climbing algorithms can get stuck at this peak and not reach the global MPP. This can result in power losses.
Modifications to the panel array may be built to employ bypass diodes, module level power electronics, or microinverters to prevent these losses. Furthermore, there are a number of MPPT algorithms that have been developed to address the challenges of nonlinear IV and PV characteristics. These algorithms typically use more sophisticated techniques than hill climbing, such as genetic algorithms (GA), particle swarm optimization (PSO), and artificial neural networks (ANN). These algorithms are able to track the MPP more accurately and efficiently, which can lead to improved power output and reduced power losses.
There are several methods proposed for MPPT, which can be broadly classified into two categories: open-loop and closed-loop methods. Open-loop methods do not require any measurement of the PV module or array current or voltage, while closed-loop methods require the measurement of the PV module or array current and voltage. Open-loop methods are simple and easy to implement, but they are also affected by environmental conditions and the PV module or array characteristics. Closed-loop methods are more accurate and efficient, but they also require more complex hardware and control algorithms.
A comparison table contrasting open-loop and closed-loop methods for MPPT is shown in Table 1. This table highlights key differences between open-loop and closed-loop methods for MPPT, emphasizing aspects such as measurement requirements, implementation complexity, accuracy, efficiency, hardware, and adaptability. It provides a quick overview to help understand the pros and cons of each approach in the context of MPPT techniques.
Table 1. Comparison between open-loop and closed-loop methods for MPPT.
Aspect Open-Loop Methods Closed-Loop Methods
Measurement Requirement No measurement of PV module/array current or voltage is needed. Requires measurement of PV module/array current and voltage.
Simplicity of Implementation Simple and easy to implement, suitable for basic setups. More complex in implementation due to measurement and control requirements.
Environmental Impact Susceptible to environmental conditions, leading to potentially reduced accuracy. Less influenced by environmental factors, offering higher accuracy.
PV Module/Array Impact Affected by PV module/array characteristics, which can lead to suboptimal performance. More accurate adaptation to PV module/array characteristics, leading to better performance.
Efficiency Typically less efficient due to limited adjustment accuracy. Generally more efficient, as they can fine-tune adjustments.
Hardware Complexity Requires simpler hardware compared to closed-loop methods. Requires more complex hardware due to measurement and feedback components.
Control Algorithms Simpler control algorithms are used for basic voltage or power adjustments. More sophisticated control algorithms are needed for precise adjustments.
Adaptability May struggle with dynamic changes or partial shading scenarios. Better adaptability to changing conditions and shading scenarios.
Applications Suited for smaller, cost-sensitive setups with minimal hardware requirements. Ideal for larger installations or scenarios requiring higher accuracy and performance.
Recently, several metaheuristic algorithms have been proposed for MPPT. Metaheuristic algorithms are optimization techniques inspired by natural processes, such as genetic algorithms (GA), particle swarm optimization (PSO), and ant colony optimization (ACO). These algorithms have demonstrated their effectiveness in solving complex and nonlinear optimization problems, including MPPT, as compared to the conventional algorithm such as “Perturb and Observe” (P&O). This method involves perturbing the operating point of the photovoltaic system and observing the resulting change in power output to determine the direction to adjust the operating point for the MPP. In one case, the conventional algorithm tracked the MPP, while for the other case it failed [5][6]. The conventional algorithm, though simple and efficient in tracking the optimal value, failed when employed for tracking power under PSC. After their failure, artificial intelligence (AI)-based algorithms, such as fuzzy logic control (FLC) [7], artificial neural network (ANN) [8][9], etc., were employed. The algorithms were proven successful in tracking the maximum power under partially shaded conditions, but the training that they required posed a huge burden on the computer’s memory. Hence, finally, the nature-inspired algorithms that were employed.
The work presented in [10] provides a thorough comparative analysis between classical and metaheuristic MPPT algorithms, specifically focusing on PV systems operating under uniform conditions. By examining the merits and limitations of various optimization strategies, the study offers valuable insights into the performance and adaptability of MPPT algorithms in scenarios where shading effects are uniform and, similarly, the significance of incorporating a comprehensive range of metaheuristic optimization algorithms. One notable contribution in this domain is in [11], which introduces a classification of evolutionary optimization methods into nine distinct categories.
The genetic algorithm (GA) is a search algorithm that is inspired by the processes of natural selection and evolution. GA can be used to find the global optimum of a function by simulating the processes of reproduction, mutation, and selection [12]. GA has been shown to be effective for MPPT, especially for PV systems with non-linear and complex characteristics [13]. Another popular metaheuristic algorithm for MPPT is particle swarm optimization (PSO). PSO is a search algorithm that is inspired by the behavior of a group of birds or fish searching for food. PSO can be used to find the global optimum of a function by simulating the processes of cooperation, competition, and adaptation [14]. PSO has been shown to be effective for MPPT, especially for PV systems with changing environmental conditions [15][16].
The work presented in [17] offers an examination of the validation process for the recently developed jellyfish search optimization (JSO) algorithm. It focuses on its application to the challenge of maximum power point tracking in solar photovoltaic (PV) systems under conditions of partial shading. The JSO algorithm, inspired by the foraging behavior of jellyfish in the ocean, operates as a swarm-insight-driven method [18]. The study in [17] presents a comprehensive exploration of the operational principles underlying the JSO strategy, visually illustrating its key operational steps. Furthermore, a simulation was conducted to assess the performance of the JSO algorithm across diverse scenarios, including static and dynamic irradiance conditions within the PV system. Moreover, the study in [19] offers a significant contribution to this discourse. This study conducted an insightful economic analysis focused on the influence of shading effects from transmission lines on investment decisions concerning photovoltaic power plants. The case study approach employed provides valuable insights into the financial considerations and implications of shading phenomena in solar energy systems. Ant colony optimization (ACO) is another metaheuristic algorithm that has been proposed for MPPT. ACO is a search algorithm that is inspired by the behavior of ants searching for food. ACO can be used to find the global optimum of a function by simulating the processes of communication, cooperation, and adaptation [20]. ACO has been shown to be effective for MPPT, especially for PV systems with changing environmental conditions and non-linear characteristics [21]. Similarly, other various nature-inspired algorithms have been used in the literature to obtain the maximum power out of a solar PV array, such as the Jaya algorithm [22], gravitational search algorithm (GSA) [23], teaching learning-based optimization (TLBO) algorithm [24], coyote optimization algorithm (COA) [25], a very commonly used PSO algorithm with various modifications [26][27], adaptive radial movement optimization (ARMO) algorithm [28], etc. These algorithms, due to their search space exploration capability that is exploited to find the optimal solution, were found very useful for MPPT applications. Their exploration property does not let them get stuck on local maxima. Moreover, they require no huge data feeds in their learning process, unlike AI-based algorithms. These algorithms differ in their performances on the basis of various parameters, such as tracking time, tracking efficiency, output fluctuations, etc.
In recent years, several hybrid metaheuristic algorithms have been proposed for MPPT that combine the advantages of different metaheuristic algorithms. For instance, a hybrid of PSO and GA, called PSOGA, has been proposed for MPPT [29], which takes the advantages of both methods by combining the exploration capability of GA with the exploitation capability of PSO. Another hybrid metaheuristic algorithm called Cuckoo Search-Particle Swarm Optimization (CS-PSO) was proposed for MPPT [30], which combines the global search capability of Cuckoo Search with the local search capability of PSO. Likewise, there are several other recently proposed hybrid metaheuristic algorithms that have been used for MPPT under PSC, such as Cat Swarm Optimization (CSO) with Firefly Algorithm (FF) [31], tunicate swarm algorithm (TSA) with the particle swarm optimization (PSO) [32], Spotted Hyena and Quadratic Approximation [33], Harris Hawk Optimization (HHO) and P&O [34], P&O using a simulated annealing (SA) algorithm [35], Particle-Swarm-Optimization-Trained Machine Learning and Flying Squirrel Search Optimization (FSSO) [36], etc. Furthermore, these hybrid metaheuristic algorithms have shown better performance in terms of convergence speed, accuracy, and robustness compared to their individual counterparts.

This entry is adapted from the peer-reviewed paper 10.3390/pr11092776

References

  1. Andrei, H.; Dogaru-Ulieru, V.; Chicco, G.; Cepisca, C.; Spertino, F. Photovoltaic Applications. J. Mater. Process. Technol. 2007, 181, 267–273.
  2. Verma, D.; Nema, S.; Shandilya, A.M.; Dash, S.K. Maximum Power Point Tracking (MPPT) Techniques: Recapitulation in Solar Photovoltaic Systems. Renew. Sustain. Energy Rev. 2016, 54, 1018–1034.
  3. Salem, F.; Awadallah, M.A. Detection and Assessment of Partial Shading in Photovoltaic Arrays. J. Electr. Syst. Inf. Technol. 2016, 3, 23–32.
  4. Vieira, R.G.; de Araújo, F.M.U.; Dhimish, M.; Guerra, M.I.S. A Comprehensive Review on Bypass Diode Application on Photovoltaic Modules. Energies 2020, 13, 2472.
  5. Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of the Incremental Conductance Maximum Power Point Tracking Algorithm. IEEE Trans. Sustain. Energy 2013, 4, 108–117.
  6. Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of Perturb and Observe MPPT Algorithm Implementation Techniques for PV Pumping Applications. IEEE Trans. Sustain. Energy 2012, 3, 21–33.
  7. Guruambeth, R.; Ramabadran, R. Fuzzy Logic Controller for Partial Shaded Photovoltaic Array Fed Modular Multilevel Converter. IET Power Electron. 2016, 9, 1694–1702.
  8. Elobaid, L.M.; Abdelsalam, A.K.; Zakzouk, E.E. Artificial Neural Network-Based Photovoltaic Maximum Power Point Tracking Techniques: A Survey. IET Renew. Power Gener. 2015, 9, 1043–1063.
  9. Hussain, M.T.; Sarwar, A.; Tariq, M.; Urooj, S.; BaQais, A.; Hossain, M.A. An Evaluation of ANN Algorithm Performance for MPPT Energy Harvesting in Solar PV Systems. Sustainability 2023, 15, 11144.
  10. El-Ghajghaj, A.; Karmouni, H.; El Ouanjli, N.; Jamil, M.O.; Qjidaa, H.; Sayyouri, M. Comparative Analysis of Classical and Meta-Heuristic MPPT Algorithms in PV Systems Under Uniform Condition. In Digital Technologies and Applications, Proceedings of the International Conference on Digital Technologies and Applications, Fez, Morocco, 27–28 January 2023; Lecture Notes in Networks and Systems; Springer: Berlin/Heidelberg, Germany, 2023; Volume 668, pp. 714–723.
  11. Akyol, S.; Alatas, B. Plant Intelligence Based Metaheuristic Optimization Algorithms. Artif. Intell. Rev. 2017, 47, 417–462.
  12. Chauhan, S.S.; KumKatoch, S.; Ar, V. A Review on Genetic Algorithm: Past, Present, and Future. Multimed. Tools Appl. 2020, 80, 8091–8126.
  13. Hilali, A.; Mardoude, Y.; Essahlaoui, A.; Rahali, A.; Ouanjli, N. El Migration to Solar Water Pump System: Environmental and Economic Benefits and Their Optimization Using Genetic Algorithm Based MPPT. Energy Rep. 2022, 8, 10144–10153.
  14. Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561.
  15. Li, H.; Yang, D.; Su, W.; Lü, J.; Yu, X. An Overall Distribution Particle Swarm Optimization MPPT Algorithm for Photovoltaic System under Partial Shading. IEEE Trans. Ind. Electron. 2019, 66, 265–275.
  16. Liu, Y.H.; Huang, S.C.; Huang, J.W.; Liang, W.C. A Particle Swarm Optimization-Based Maximum Power Point Tracking Algorithm for PV Systems Operating under Partially Shaded Conditions. IEEE Trans. Energy Convers. 2012, 27, 1027–1035.
  17. Alam, A.; Verma, P.; Tariq, M.; Sarwar, A.; Alamri, B.; Zahra, N.; Urooj, S. Jellyfish Search Optimization Algorithm for Mpp Tracking of Pv System. Sustainability 2021, 13, 11736.
  18. Chou, J.S.; Truong, D.N. A Novel Metaheuristic Optimizer Inspired by Behavior of Jellyfish in Ocean. Appl. Math. Comput. 2021, 389, 125535.
  19. Zsiborács, H.; Baranyai, N.H.; Vincze, A.; Pintér, G. An Economic Analysis of the Shading Effects of Transmission Lines on Photovoltaic Power Plant Investment Decisions: A Case Study. Sensors 2021, 21, 4973.
  20. Dorigo, M.; Stützle, T. Ant Colony Optimization: Overview and Recent Advances. Int. Ser. Oper. Res. Manag. Sci. 2019, 272, 311–351.
  21. Krishnan, G.; Satheesh; Kinattingal, S.; Simon, S.P.; Nayak, P.S.R. MPPT in PV Systems Using Ant Colony Optimisation with Dwindling Population. IET Renew. Power Gener. 2020, 14, 1105–1112.
  22. Huang, C.; Zhang, Z.; Wang, L.; Song, Z.; Long, H. A Novel Global Maximum Power Point Tracking Method for PV System Using Jaya Algorithm. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017.
  23. Pervez, I.; Sarwar, A.; Tayyab, M.; Sarfraz, M. Gravitational Search Algorithm (GSA) Based Maximum Power Point Tracking in a Solar PV Based Generation System. In Proceedings of the 2019 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 22–23 March 2019.
  24. Rezk, H.; Fathy, A. Simulation of Global MPPT Based on Teaching–Learning-Based Optimization Technique for Partially Shaded PV System. Electr. Eng. 2017, 99, 847–859.
  25. Pervez, I.; Sarwar, A.; Pervez, A.; Tariq, M.; Zaid, M. Maximum Power Point Tracking of a Partially Shaded Solar PV Generation System Using Coyote Optimization Algorithm (COA). In Advances in Electromechanical Technologies, Proceedings of the TEMT 2019, International Conference on Emerging Trends in Electro-Mechanical Technologies and Management, New Delhi, India, 26–27 July 2019; Lecture Notes in Networks and Systems; Springer: Berlin/Heidelberg, Germany, 2020; pp. 509–518.
  26. Pervez, I.; Sarwar, A.; Pervez, A.; Tariq, M.; Zaid, M. An Improved Maximum Power Point Tracking (MPPT) of a Partially Shaded Solar PV System Using PSO with Constriction Factor (PSO-CF). In Advances in Electromechanical Technologies, Proceedings of the TEMT 2019, International Conference on Emerging Trends in Electro-Mechanical Technologies and Management, New Delhi, India, 26–27 July 2019; Lecture Notes in Networks and Systems; Springer: Berlin/Heidelberg, Germany, 2020; pp. 499–507.
  27. Lian, K.L.; Jhang, J.H.; Tian, I.S. A Maximum Power Point Tracking Method Based on Perturb-and-Observe Combined with Particle Swarm Optimization. IEEE J. Photovolt. 2014, 4, 626–633.
  28. Seyedmahmoudian, M.; Soon, T.K.; Horan, B.; Ghandhari, A.; Mekhilef, S.; Stojcevski, A. New ARMO-Based MPPT Technique to Minimize Tracking Time and Fluctuation at Output of PV Systems under Rapidly Changing Shading Conditions. IEEE Trans. Ind. Inform. 2019.
  29. Badis, A.; Mansouri, M.N.; Sakly, A. PSO and GA-Based Maximum Power Point Tracking for Partially Shaded Photovoltaic Systems. In Proceedings of the 2016 7th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 22–24 March 2016.
  30. Senthilkumar, S.; Mohan, V.; Deepa, R.; Nuthal Srinivasan, M.; Senthil Kumar, T.; Thanikanti, S.B.; Prathap, N. A Review on Mppt Algorithms for Solar Pv Systems. Int. J. Res.-GRANTHAALAYAH 2023, 11, 25–64.
  31. Thangam, T.; Muthuvel, K. PFoPID CONTROL DESIGN OF GRID-CONNECTED PV INVERTER FOR MPPT USING HYBRID ALGORITHM. Int. J. Power Energy Syst. 2022, 42, 1–8.
  32. Sharma, A.; Sharma, A.; Jately, V.; Averbukh, M.; Rajput, S.; Azzopardi, B. A Novel TSA-PSO Based Hybrid Algorithm for GMPP Tracking under Partial Shading Conditions. Energies 2022, 15, 3164.
  33. Kumar, P.; Kumar, M.; Bansal, A.K. GMPP Tracking of Solar PV System Using Spotted Hyena and Quadratic Approximation Based Hybrid Algorithm under Partially Shaded Conditions. IEEE Access 2023.
  34. Hafeez, M.A.; Naeem, A.; Akram, M.; Javed, M.Y.; Asghar, A.B.; Wang, Y. A Novel Hybrid MPPT Technique Based on Harris Hawk Optimization (HHO) and Perturb and Observer (P&O) under Partial and Complex Partial Shading Conditions. Energies 2022, 15, 5550.
  35. Abo-Khalil, A.G.; El-Sharkawy, I.I.; Radwan, A.; Memon, S. Influence of a Hybrid MPPT Technique, SA-P&O, on PV System Performance under Partial Shading Conditions. Energies 2023, 16, 577.
  36. Kumar, D.; Chauhan, Y.K.; Pandey, A.S.; Srivastava, A.K.; Kumar, V.; Alsaif, F.; Elavarasan, R.M.; Islam, M.R.; Kannadasan, R.; Alsharif, M.H. A Novel Hybrid MPPT Approach for Solar PV Systems Using Particle-Swarm-Optimization-Trained Machine Learning and Flying Squirrel Search Optimization. Sustainability 2023, 15, 5575.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
Video Production Service
Feedback