In a market, there are always have two sides, buyers and sellers. They have their willingness price before they make a trade in the market, here willingness price means what they would pay or sell for the deal. when the buyer's willingness price is higher than the seller's willingness price, they will trade successfully. Considering that, we know that there we cannot always get what we want. Except this thing, quantity of total demand and total supply are also important. If buyers want 100 goods, but there are 50 goods can be sold, we can know that just half of buyers can get what they want. Following these two principles, we use entropy to measure the market uncertainty. That is Transaction entropy. Transaction entropy is defined as the ratio of the total information entropy of all traders to the quantity of transactions, reflecting the level of uncertainty in making successful transactions. Based on the computational and simulated results, our main finding is that transaction entropy is the lowest at equilibrium, it will decrease in a shortage market, and increase in a surplus market. Additionally, we make a comparison of the total entropy of the centralized market with that of the decentralized market, revealing that the price-filtering mechanism could effectively reduce market uncertainty. Overall, the introduction of transaction entropy enriches our understanding of market uncertainty and facilitates a more comprehensive assessment of market performance.
- entropy
- market uncertainty
1.Introduction
The concept of the market holds great significance in economics and serves as a fundamental basis for research of economics [1]. Understanding the mechanisms by which markets function has profound implications for decision making, policy formulation, and economic development. The research on market primary functioning has long been focused on two key aspects: price formation and market efficiency. In the context of market price, this is determined by the interaction between sellers and buyers. In a perfect competitive market, the market price is deemed to be at the cross point of the supply and demand curves. Therefore, the factors that influence these curves, such as the willingness of the market participants and information dissemination, have impacts on the level of the market price. Regarding market efficiency, market surplus is usually used to measure it. Market surplus represents the total welfare generated by transactions between sellers and buyers. An increase in market surplus signifies an improved efficiency in market transactions and a more optimal allocation of resources. However, most analyses of price formation and market efficiency are typically conducted under the assumption of ideal conditions, without accounting for the uncertainties faced by the participants in a market. Several studies have verified the existence of uncertainties in market transactions [2][3]. During an actual transaction process, each participant has limited access to information and cannot obtain complete knowledge about the counterparty's information or the overall market situation. This inherent imperfection in information significantly influences the decision making and behavior of both parties involved, thereby increasing transactional uncertainty, which subsequently impacts market prices and market surplus. Therefore, understanding the mechanism of price formation and improving market efficiency have become the cornerstones of economic analyses, and we contend that incorporating uncertainty into a market can not only provide a more accurate description of market performance, but also enrich our understanding of market functioning.
2.Transaction Entropy
At first, we use PEA to obtain supply and demand curves. A partial equilibrium analysis (PEA) is a widely used tool for understanding market performance. It argues that supply and demand collectively represent two sides of traders in a market, making it simple to analyze the consequence of their interaction by tracing the equilibrium point and social welfare implications [4]. However, the PEA also needs to be improved, since it fails to clearly identify how sellers and buyers constitute supply and demand curves correspondingly. To solve this problem, Wang and Stanley introduced the concept of willingness price and formulated supply and demand functions to restate the PEA in a goods market [5]. The major advantage of this approach is that the laws of supply and demand can be derived directly, and the efficiency of market equilibrium can be strictly proved.
According to the analyses in description, we know that it is uncertain that if a buyer or a seller can trade successfully. Therefore, we can use the information entropy proposed by Shannon to present the uncertainty of trader's transaction in the market[6]. The definition of information entropy for individual traders H(E) can be written as
H(E) = −[E ∗ ln(E) + (1 − E) ∗ ln(1 − E)],
where E is the possibility of a successful trade. After we get one trader's entropy, we can get the total entropy in the market TS, which can be defined as the sum of the information entropy for individual trader in the market. The TS indicates that the resulting information entropy contains the contributions of all the actual transactions. To eliminate the effect of the market scale on the information entropy, we define the transaction entropy generated by one transaction to measure the market performance. Then, the transaction entropy takes the following form Then we can define the transaction entropy S as follows;
S=TS/T,
Where T is the quantity of transaction in the market. Transaction is helpful to measure the market performance.
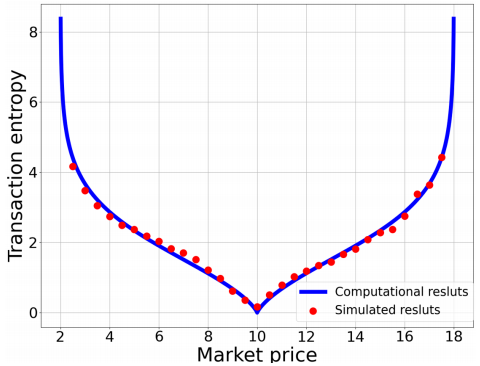
3.Total Entropy in different market
We can not only use transaction entropy to describe the performance of a market, but also, we can use the total entropy TS to measure the uncertainty for the trade in the market. There are two kinds of market: centralized market and decentralized market. A market is a centralized market when there is a central information collector, like market dealer. When the buyers and sellers have random matching, we say there is a decentralized market. We can find that there is less entropy in the centralized market. The results shown in the following picture means that there is more efficient in a centralized market where the market dealer can get the willingness prices of buyers and sellers, such as a stock market. And in fact, it also indicates that we can improve our market by dealing with information more properly.
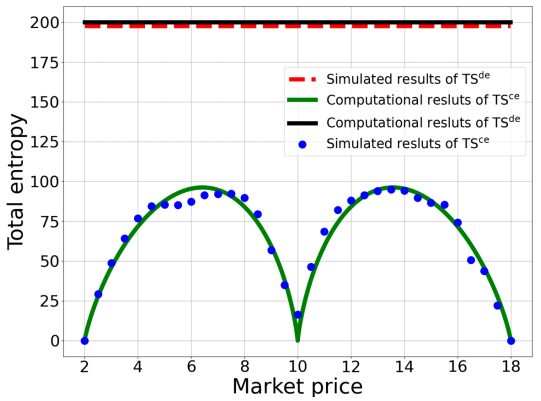
4. Discussion
equilibrium assume that information of the willingness prices of traders is available, and traders engage in reverse rank matching when they make transactions. However, these assumptions are unrealistic, and the willingness prices of traders can only guide them to choose whether to enter market or not. Once they have entered a market, they are randomly matched to trade with each other, which must incur uncertainty in transactions.
References
- Buzzell, R.D. Market Functions and Market Evolution. J. Mark. 1999, 63, 61–63.
- Jurado, K.; Ludvigson, S.C.; Ng, S. Measuring Uncertainty. Am. Econ. Rev. 2015, 105, 1177–1216.
- Sniazhko, S. Uncertainty in Decision-Making: A Review of the International Business Literature. Cogent Bus. Manag. 2019,6, 1650692.
- Wigle, R. Partial Equilibrium Analysis: A Primer; Wilfrid Laurier University: Waterloo, ON, Canada, 2004.
- Yougui, Wang; H. E. Stanley. Statistical approach to partial equilibrium analysis. Phys. A Stat. Mech. Appl. 2009, 388, 1173–1180.
- Bouattour, M.; Martinez, I. Efficient Market Hypothesis: An Experimental Study with Uncertainty and Asymmetric Information.Financ. Contrôle Strat. 2019, 22, 4.
