Resilience Optimization of Post-Quantum Cryptography Key Encapsulation Algorithms: History
View Latest Version
Please note this is an old version of this entry, which may differ significantly from the current revision.
Contributor:
Sana Farooq
,
Ayesha Altaf
,
Faiza Iqbal
,
Ernesto Bautista Thompson
,
Debora Libertad Ramírez Vargas
,
Isabel de la Torre Díez
,
Imran Ashraf

The developments in quantum computing have shed light on the shortcomings of the conventional public cryptosystem. Even while Shor’s algorithm cannot yet be implemented on quantum computers, it indicates that asymmetric key encryption will not be practicable or secure in the near future. The National Institute of Standards and Technology (NIST) has started looking for a post-quantum encryption algorithm that is resistant to the development of future quantum computers as a response to this security concern. 

  • cryptography
  • post-quantum cryptography
  • asymmetric cryptography

1. Introduction

Cryptography is a method of protecting data in the presence of unauthorized users by establishing a secure communication channel between two parties. This technique was developed by the Institute of Electrical and Electronics Engineers (IEEE). Encryption and decryption are the two processes that are carried out in cryptography by both the sender and the receiver. The process of converting unencoded data into an encoded format referred to as a “Cipher” using a safe data source is what we mean when we talk about encryption (key). Decryption is the process of converting encrypted data back into its original plain form using either the same secure data source (key) or a different secure data source [1]. This process is the inverse of encryption.
There are two distinct categories of cryptographic methods: symmetric and asymmetric. The process of the encryption and decryption of data in symmetric cryptography only requires the use of a single key. A private key is utilized to carry out this method. This refers to the requirement that a private key must be guarded in secrecy and given out to a sender and recipient who are authorized to do so. The process of symmetric cryptography is illustrated in Figure 1a. For encryption and decryption, asymmetric cryptography, also known as public key cryptography, employs a key pair. One of the keys in the key pair is a publicly accessible key. The sender will use a public key for encryption, while the recipient will use the private key, which is only known to them [2]. Figure 1b depicts the operation of an asymmetrical cryptography system.
Figure 1. Types of cryptography, (a) symmetric cryptography, and (b) asymmetric cryptography.
The use of quantum computers, with their unfathomable computing power, is rapidly approaching reality [3]; it is no longer a dream. A computer based on the peculiar properties of quantum mechanics can perform calculations exponentially faster than a computer made of classical bits. In October 2019, Google announced the development of a quantum computer that samples the output of a pseudo-random quantum circuit ten-times faster than the fastest supercomputers available today [4]. Recent developments in quantum computing pose a threat to public key primitives [5] due to quantum computers’ ability to solve complex cryptographic problems in polynomial time. post-quantum cryptography (PQC) refers to asymmetric cryptographic algorithms that can withstand attacks from a quantum computer.
The National Institute of Standards and Technology (NIST) is currently developing a new generation of quantum-resistant key encapsulation and authentication schemes [6] to combat this threat to essential Internet security protocols such as transport layer security (TLS). TLS [7] is the most-popularly employed secure communication protocol for online page transfers, encrypted email server access, and mobile applications. The majority of hypertext transfer protocol (HTTPS) service connections utilize TLS [8]. TLS uses Rivest–Shamir–Adleman (RSA) or elliptic curve (EC) signatures and Diffie–Hellman (DH) with EC for key exchange. It is crucial to plan the transition to quantum-resistant schemes, such as Secure Hashing Algorithm-2 (SHA-2) and elliptic curve digital signature algorithm (EC), which were not adopted until a decade after their standardization [9][10], given that the adoption of cryptographic techniques could take years. It is important to note that increasing the hash size of SHA-2 does not give essential protection against quantum assaults. Larger hash sizes can provide temporary mitigation against some attacks, but they are not an adequate remedy [11]. Quantum computers can still potentially break cryptographic schemes based on hash functions by using algorithms specifically designed for quantum computing. It is necessary to adopt algorithms and protocols that are designed explicitly to survive the assaults of quantum computers. These methods typically rely on mathematical problems that both classical and quantum computers both find hard to solve.

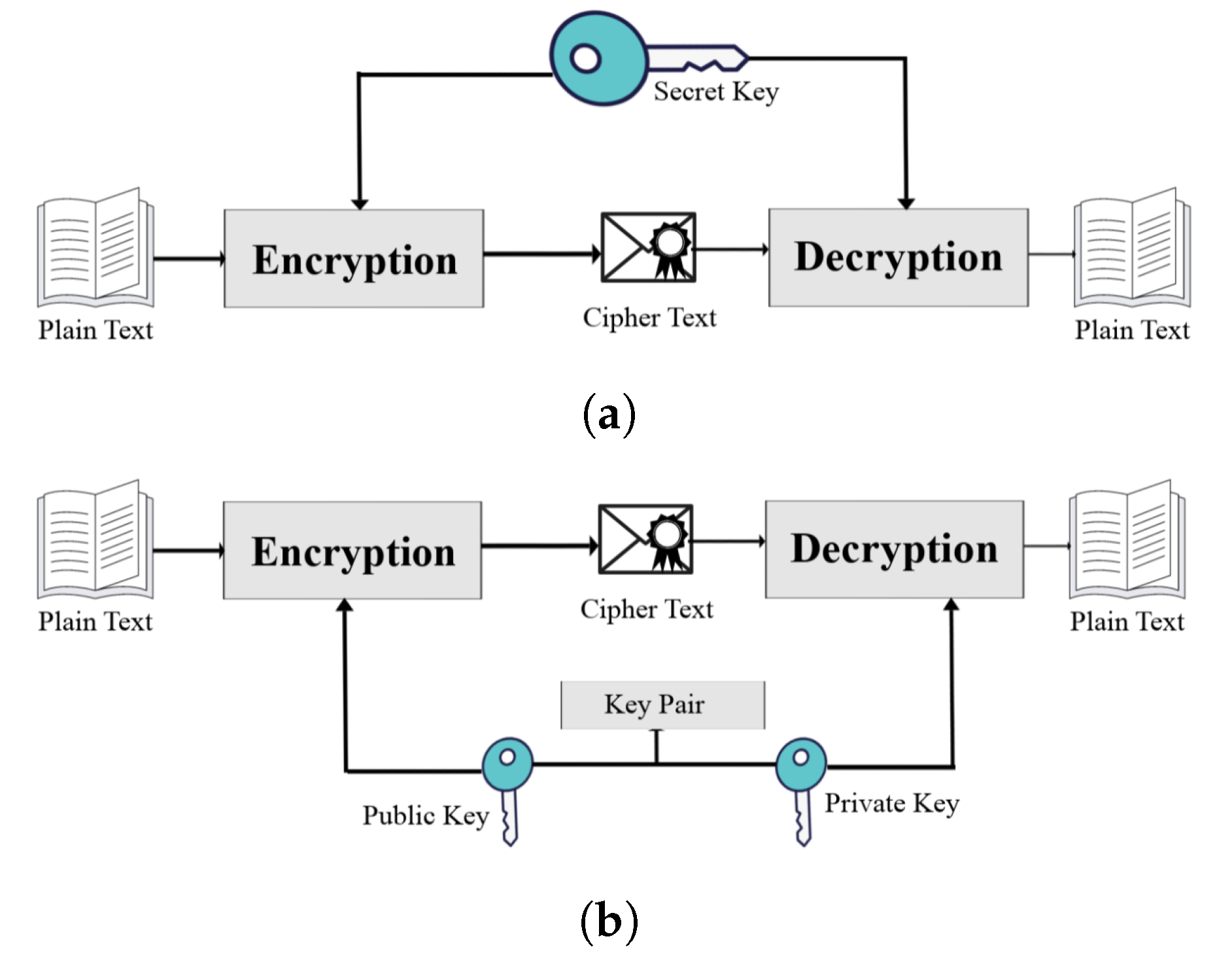
2. Resilience Optimization of Post-Quantum Cryptography Key Encapsulation Algorithms

As the power of quantum computers increases in the foreseeable future, we must consider how this will affect Internet security. Given the power of quantum computing, significant research effort is being devoted to solving the difficult problems used in modern cryptography, which is expected to have a significant impact on the security of current classic public key cryptosystems in the near future.
PQC refers to asymmetric cryptographic methods that are immune to quantum-computer-based attacks. Shor’s algorithm was one of the first to demonstrate that three problems that serve as the foundation of classical public key cryptography can be solved in polynomial time by a quantum computer’s exponential computing power. Shor’s algorithm, which has the potential to break a number into prime factors in polynomial time, poses a threat to all currently popular asymmetric algorithms based on the integer factorization problem, such as RSA, the discrete logarithm problem, elliptic curve cryptography (ECC), and elliptic curve discrete logarithm (ECDH) [12]. Even if there are no quantum computers capable of running Shor’s algorithm on a reasonably sized asymmetric key today, one will exist in the future [13].
Due to the aforementioned circumstances, it is becoming increasingly important to design a new quantum-safe encryption and authentication system that is not based on the difficult problems of classical public key cryptography. TLS’s handshake protocol heavily depends on variants of RSA, DH, and EC for signing and key exchange. In order to be resistant to quantum computers, these algorithms must be replaced with PQC algorithms. Several post-quantum cryptography alternatives have been proposed. The current five families of PQC systems are code-based, lattice-based, hash-based, multivariate, and supersingular elliptic curve isogeny cryptography. The most-developed digital signature methods are hash-based. They were presented for the first time in 1979 by Lamport [14], Merkle, and Winternitz and have since undergone significant enhancements [15]. They provide a high level of security and have been evaluated thoroughly. Ajtai introduced lattice-based cryptography for the first time in 1996 [16]. In comparison to other PQC families, it offers highly effective key encapsulation techniques. In contrast to hash-based techniques, however, their security is less well known.
KEM and SIG algorithms are both required for establishing a shared key and verifying the authentication of two parties. Similar to previous NIST efforts to standardize various sub-fields of cryptography, most notably the 2001 standardization of AES, NIST is currently engaged in a project to standardize PQC algorithms. Numerous research analyses on the PQC algorithms and their alternatives that have been presented and advanced to the third round of the NIST standardization competition have already been conducted. Two additional classifications exist for algorithms. The KEM algorithm is used for key exchange, while the SIG algorithm is used for sender authentication. The key encapsulation mechanisms and SIG algorithms [16][17] are displayed in Table 1.
Table 1. KEM and SIG algorithms—NIST PQC third-round finalists and alternate candidates.
Key Encapsulation Algorithms Signature Algorithms
Classic McEliece CRYSTALS-Dilithium
CRYSTALS-Kyber Falcon
NTRU Rainbow
Saber  
BIKE GeMSS
HQC SPHINCS+
FrodoKEM Picnic
NTRU Prime  

Table 2 and Table 3 display related work on PQC algorithms and signatures for performance evaluation.

Table 2. Summary of related work on PQC key exchange algorithms.
Ref. Key Exchange Algorithm NIST Security Level Public Key Length (Bytes) Private Key Length (Bytes) Cipher Text Length (Bytes) Key Gen Encaps Decaps Key Exchange Mechanism
[18] NewHope × × × × ✓ ✓ ✓ ×
Kyber × × × × ✓ ✓ ✓ ×
NTRU × × × × ✓ ✓ ✓ ×
Frodo × × × × ✓ ✓ ✓ ×
[6] Kyber-512 1 800 1632 736 ✓ ✓ ✓ ×
NewHope-512-CCA 1 928 1888 1120 ✓ ✓ ✓ ×
Kyber-768 3 1184 2400 1088 ✓ ✓ ✓ ×
NTRU-HRSS-701 3 1138 1450 1138 ✓ ✓ ✓ ×
[19] Kyber-512 1 × × × × × × ✓
Kyber-768 3 × × × × × × ✓
Kyber-1024 5 × × × × × × ✓
HQC-128 1 × × × × × × ✓
HQC-192 3 × × × × × × ✓
HQC-256 5 × × × × × × ✓
SIDH-p434 1 × × × × × × ✓
SIDH-p610 3 × × × × × × ✓
SIDH-p751 5 × × × × × × ✓
[20] Kyber × 800 1632 736 ✓ ✓ ✓ ×
NTRU × 930 1234 930 ✓ ✓ ✓ ×
NTRU × 1138 1450 1138 ✓ ✓ ✓ ×
Saber × 672 1568 736 ✓ ✓ ✓ ×
FrodoKEM × 9616 19,888 9720 ✓ ✓ ✓ ×
SIKE × 330 374 346 ✓ ✓ ✓ ×
SIKE × 378 434 402 ✓ ✓ ✓ ×
Kyber × 378 434 402 ✓ ✓ ✓ ×
NTRU × 1230 1590 1230 ✓ ✓ ✓ ×
Saber × 992 2304 1088 ✓ ✓ ✓ ×
FrodoKEM × 15,632 31,296 15,744 ✓ ✓ ✓ ×
NTRU Prime × 1158 1763 1039 ✓ ✓ ✓ ×
NTRU Prime × 1039 1294 1167 ✓ ✓ ✓ ×
SIKE × 462 524 486 ✓ ✓ ✓ ×
Kyber × 1568 3068 1568 ✓ ✓ ✓ ×
Saber × 1312 3040 1472 ✓ ✓ ✓ ×
SIKE × 564 644 596 ✓ ✓ ✓ ×
Table 3. Related work on PQC signature algorithms.
Ref. PQC Signature Algorithm NIST Security Level Public Key Length (Bytes) Private Key Length (Bytes) Signature Length (Bytes) Sign Verify
[6] Dilithium 2 1472 3504 2701 ✓ ✓
SPHINCS+ SHA256-128f 1 32 64 16,976 ✓ ✓
Dilithium 3 1760 3856 3366 ✓ ✓
SPHINCS+ SHA256-192f- 3 48 96 35,664 ✓ ✓
[19] Falcon-512 1 × × × ✓ ✓
Falcon-1024 5 × × × ✓ ✓
Rainbow-I-Classic 1 × × × ✓ ✓
Rainbow-III-Classic 3 × × × ✓ ✓
Rainbow-V-Classic 5 × × × ✓ ✓
SPHINCS+-SHAKE256-128f-Robust 1 × × × ✓ ✓
SPHINCS+-SHAKE256-192f-Robust 3 × × × ✓ ✓
SPHINCS+-SHAKE256-256f-Robust 5 × × × ✓ ✓
[20] Dilithium × 1184 2800 2044 × ×
Falcon × 1281 897 690 × ×
Falcon × 57,344 897 690 × ×
Dilithium × 1472 3504 2701 × ×
Dilithium × 1760 3856 3366 × ×
Falcon × 1793 2305 1330 × ×
In the era of the Internet of Things (IoT), NIST is concurrently conducting the Lightweight Cryptography Standardization Process (LWC-SP), which aims to select lightweight cryptographic algorithms for standardization. This process ensures that the chosen algorithms are secure, efficient, and suitable for resource-constrained devices. Extensive research has been conducted over the years on various lightweight cryptographic algorithms, studying their principles, techniques, and countermeasures against fault attacks. These studies provide valuable insights into the vulnerabilities and propose effective mitigation strategies in the context of lightweight cryptography. Prominent algorithms in this field include Pomaranch Cipher [21], Grostl Hash, Midori Cipher [22], RECTANGLE Cipher [23], and Ascon [24]. Notably, in the latest updates in February 2023, NIST has finalized the standardization of the Ascon algorithm as part of the LWC-SP. The updates from NIST affirm that Ascon is a secure and efficient lightweight block cipher. Ascon demonstrates versatility in implementation across different platforms and exhibits resistance against various attack vectors. Given these qualities, Ascon emerges as a favorable option for deployment in resource-constrained devices [25]. Evaluating the PQC algorithms for lightweight cryptography or embedded systems is of utmost importance. Therefore, researchers have been studying and conducting evaluations of PQC algorithms on ARM Cortex M4 processors to establish benchmarks [20].
Classic McEliece is the oldest cryptosystem proposed in Round 4 of the NIST PQC standard [26] submissions. Based on the 1979 McEliece cryptosystem that employed secret Goppa codes, the original cryptosystem was not designed to adhere to restrictions on public use computation. Researchers in the field of cryptography have thoroughly examined and analyzed the McEliece cryptosystem during the course of its history. Numerous assaults have been considered and planned, but none have been able to undermine the scheme’s entirety. The following notable assaults have been investigated:
  • Information set decoding (ISD) attack:This attack served as the foundation for the initial assault plan against McEliece. This approach attempted to discover a small set of linearly dependent syndromes in order to retrieve the private key. It was later demonstrated, though, that, with appropriate parameter selection, this attack is not possible.
  • Square root attack: This attack was introduced in the context of McEliece variants, such as the Niederreiter cryptosystem. This attack tries to recover the private key by taking advantage of the algebraic structure of the cryptosystem’s code. This attack, however, is only relevant to certain parameter selections and is not seen as being practical against versions of McEliece that have been properly configured [27].
  • Meet-in-the-middle attack: This attack tries to exploit the error-correction capability of the code and the encoding process to retrieve the private key. This assault, however, needs an excessive amount of processing power and is not seen as a viable threat.
Classic McEliece provides security against chosen ciphertext attack (CCA). When the message is selected at random, an attacker cannot decipher the message efficiently using the cipher text and public key. The original cryptosystem offered security against one-way CCA, meaning an attacker cannot efficiently decipher a message from a ciphertext and a public key when the message is chosen at random [28]. This system combines NTS-KEM and classic McEliece in order to provide efficient implementation and CCA security. It implements the hashing of errors added to the cipher text and relies on the security provided by hash functions. It is a defense against CCA attacks.
It is important to be aware of various sorts of attacks so that practical defenses against these threats can be evaluated in future research. The side-channel attacks (SCAs) can exploit information leaked through the physical characteristics of the cryptographic implementation. Two common types of SCAs are fault attacks and power analysis attacks.
Fault attacks include introducing faults or errors within the cryptographic system on purpose to obtain unauthorized access or extract sensitive information. An attacker can compel the system to act unexpectedly by changing the execution environment, potentially disclosing private keys or other confidential data. Fault attacks can be a serious threat to the security of cryptographic devices. To preserve the integrity and security of cryptographic operations, countermeasures against fault attacks include techniques such as redundancy, error detection, error correction, and fault-tolerant-designed cryptography devices [29]. In contrast, power analysis attacks seek to leverage power consumption patterns or electromagnetic radiation released during cryptographic operations. An attacker can learn about the secret keys or intermediate values utilized in the calculations by analyzing these side-channel signals. Techniques such as power-analysis-resistant designs, randomizing power usage, and implementing secure masking systems are examples of countermeasures against power analysis attacks [30].
In combined attacks, adversaries combine numerous attack strategies to maximize their chances of success. A combined fault and power analysis attack, for example, may include generating faults in the system while concurrently monitoring power usage to obtain sensitive information. Assessing and managing the risks associated with combination assaults requires a thorough examination of the system’s resistance to both fault and power analysis attacks.

This entry is adapted from the peer-reviewed paper 10.3390/s23125379

References

  1. Lakshmi, P.S.; Murali, G. Comparison of classical and quantum cryptography using QKD simulator. In Proceedings of the 2017 International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS), Chennai, India, 1–2 August 2017; pp. 3543–3547.
  2. Patil, P.A.; Boda, R. Analysis of cryptography: Classical verses quantum cryptography. Int. Res. J. Eng. Technol. 2016, 3, 1372–1376.
  3. Roush, W. The Google-IBM Quantum Supremacy Fued. 2020. Available online: https://www.technologyreview.com/2020/02/26/905777/google-ibm-quantum-supremacy-computing-feud/ (accessed on 7 February 2023).
  4. Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510.
  5. Prantl, T.; Prantl, D.; Bauer, A.; Iffländer, L.; Dmitrienko, A.; Kounev, S.; Krupitzer, C. Benchmarking of pre-and post-quantum group encryption schemes with focus on IoT. In Proceedings of the 2021 IEEE International Performance, Computing, and Communications Conference (IPCCC), Austin, TX, USA, 29–31 October 2021; pp. 1–10.
  6. Sikeridis, D.; Kampanakis, P.; Devetsikiotis, M. Assessing the overhead of post-quantum cryptography in TLS 1.3 and SSH. In Proceedings of the 16th International Conference on emerging Networking Experiments and Technologies, Barcelona, Spain, 1–4 December 2020; pp. 149–156.
  7. Razaghpanah, A.; Niaki, A.A.; Vallina-Rodriguez, N.; Sundaresan, S.; Amann, J.; Gill, P. Studying TLS usage in Android apps. In Proceedings of the 13th International Conference on emerging Networking Experiments and Technologies, Incheon, Republic of Korea, 12–15 December 2017; pp. 350–362.
  8. Google Transparency Report—HTTPS Encryption on the Web. Available online: https://transparencyreport.google.com/https/overview (accessed on 19 January 2023).
  9. ANSI. Public Key Cryptography for the Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA); X9-Financial Services; American National Standards Institute: New York, NY, USA, 2005.
  10. ECDSA: The Digital Signature Algorithm of a Better Internet. Available online: https://blog.cloudflare.com/ecdsa-the-digital-signature-algorithm-of-a-better-internet (accessed on 19 January 2023).
  11. Hosoyamada, A.; Sasaki, Y. Quantum Collision Attacks on Reduced SHA-256 and SHA-512. Cryptology ePrint Archive, Paper 2021/292. 2021. Available online: https://eprint.iacr.org/2021/292 (accessed on 25 January 2023).
  12. Gidney, C.; Ekerå, M. How to factor 2048 bit RSA integers in 8 h using 20 million noisy qubits. Quantum 2021, 5, 433.
  13. Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332.
  14. Merkle, R.C. A certified digital signature. In Proceedings of the CRYPTO 1989: Advances in Cryptology—CRYPTO’89 Proceedings, Houthalen, Belgium, 10–13 April 1989; Springer: New York, NY, USA, 2001; pp. 218–238.
  15. Ajtai, M. Generating hard instances of lattice problems. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 99–108.
  16. Alagic, G.; Alperin-Sheriff, J.; Apon, D.; Cooper, D.; Dang, Q.; Kelsey, J.; Liu, Y.K.; Miller, C.; Moody, D.; Peralta, R.; et al. Status Report on the Second Round of the NIST Post-Quantum Cryptography Standardization Process; US Department of Commerce, NIST: Gaithersburg, MD, USA, 2020.
  17. Moody, D. Let’s get ready to rumble. the nist pqc competition. In Proceedings of the First PQC Standardization Conference, Fort Lauderdale, FL, USA, 11–13 April 2018.
  18. Churi, J.D. Post-Quantum Encryption Benchmark. 2020. Available online: https://digitalcommons.calpoly.edu/eesp/500/ (accessed on 15 December 2022).
  19. Döring, R.; Geitz, M. Post-Quantum Cryptography in Use: Empirical Analysis of the TLS Handshake Performance. In Proceedings of the NOMS 2022–2022 IEEE/IFIP Network Operations and Management Symposium, Budapest, Hungary, 25–29 April 2022; pp. 1–5.
  20. Strand, M. A Status Update on Quantum Safe Cryptography. In Proceedings of the 2021 International Conference on Military Communication and Information Systems (ICMCIS), The Hague, The Netherlands, 4–5 May 2021; pp. 1–7.
  21. Cid, C.; Gilbert, H.; Johansson, T. Cryptanalysis of Pomaranch. IEE Proc. Inf. Secur. 2006, 153, 51–53.
  22. Li, W.; Liao, L.; Gu, D.; Cao, S.; Wu, Y.; Li, J.; Zhou, Z.; Guo, Z.; Liu, Y.; Liu, Z. Ciphertext-only fault analysis on the Midori lightweight cryptosystem. Sci. China Inf. Sci. 2020, 63, 139112.
  23. Aghaie, A.; Kermani, M.M.; Azarderakhsh, R. Fault diagnosis schemes for secure lightweight cryptographic block cipher RECTANGLE benchmarked on FPGA. In Proceedings of the 2016 IEEE International Conference on Electronics, Circuits and Systems (ICECS), Monte Carlo, Monaco, 11–14 December 2016; pp. 768–771.
  24. Ramezanpour, K.; Ampadu, P.; Diehl, W. A Statistical Fault Analysis Methodology for the Ascon Authenticated Cipher. In Proceedings of the 2019 IEEE International Symposium on Hardware Oriented Security and Trust (HOST), McLean, VA, USA, 5–10 May 2019; pp. 41–50.
  25. Lightweight Cryptography Standardization Process: NIST Selects Ascon. Available online: https://csrc.nist.gov/News/2023/lightweight-cryptography-nist-selects-ascon (accessed on 29 May 2023).
  26. Alagic, G.; Apon, D.; Cooper, D.; Dang, Q.; Dang, T.; Kelsey, J.; Lichtinger, J.; Miller, C.; Moody, D.; Peralta, R.; et al. Status Report on the Third Round of the NIST Post-Quantum Cryptography Standardization Process; US Department of Commerce, NIST: Gaithersburg, MD, USA, 2022.
  27. McEliece, R.J. A Public Key Cryptosystem Based on Algebraic Coding Theory. 1978; pp. 114–116. Available online: https://ntrs.nasa.gov/api/citations/19780016269/downloads/19780016269.pdf#page=123 (accessed on 20 May 2023).
  28. Classic McEliece: Introduction. Available online: https://classic.mceliece.org/ (accessed on 19 January 2023).
  29. Benot, O. Fault Attack. In Encyclopedia of Cryptography and Security; van Tilborg, H.C.A., Jajodia, S., Eds.; Springer: Boston, MA, USA, 2011; pp. 452–453.
  30. Power Analysis. Available online: https://en.wikipedia.org/wiki/Power_analysis (accessed on 20 May 2023).
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
This entry is offline, you can click here to edit this entry!
Video Production Service
Feedback