Encyclopedia
Please note this is an old version of this entry, which may differ significantly from the current revision.
Traditional technologies of personal identity authentication (e.g., tokens, cards, PINs) have been gradually replaced by some more-advanced biometrics technologies, including faces, retinas, irises, fingerprints, veins, etc. Among these, the finger vein (FV) trait, due to its unique advantages of high security, the living requirement, being non-contact, and not easily being injured or counterfeited, has drawn extensive attention after it appeared. Different from some visual imaging traits such as faces and fingerprints, the main veins in the fingers tend to be longitudinally distributed in the subcutaneous regions.
- finger vein verification
- Siamese network
- contrastive learning
- Gabor convolutional kernel
1. Introduction
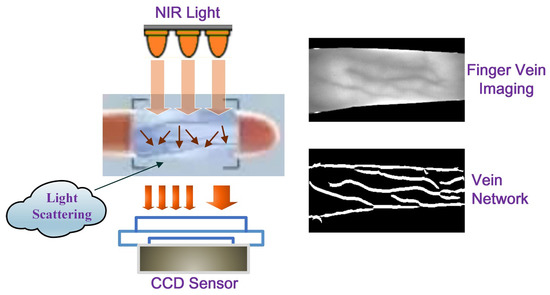
Generally, FV imaging can be performed by using near-infrared (NIR) light in the particular wavelength range of (700∼1000 nm). When the NIR light irradiates the skin and enters the subcutaneous tissues, light scattering occurs, and plenty of light energy is absorbed by the deoxyhemoglobin in the veins’ blood, which makes the veins appear as dark shadows during imaging, while other non-vein areas show higher brightness. As a result, the acquired FV images generally present a crisscross pattern, as shown in Figure 1.
Figure 1. Illustration of the appearance of finger vein imaging.
When the FV trait is used for personal identity verification, it should not be regarded as a conventional pattern-classification problem, due to the fact that the number of categories is huge, while the number of samples per category is small, and it occurs in a subject-independent scenario with only a subset of categories known during the training phase. Moreover, because of the restrictions of the acquisition equipment and environment, the imaging area of the vein texture is small [3] and the information carried by the vein image is relatively weak. In this regard, how to extract more-robust and -discriminative FV features is particularly critical for an FV verification system [4].
In the early stages of research, some meticulously hand-crafted features were adopted by FV verification systems. One kind of method, namely “vein-level” [5], was devoted to characterizing the geometric and topological shapes of the vein network (such as point-shaped [6,7,8,9], line-shaped [10,11], curve-based [12,13,14], etc.). In addition, anatomical structures [15,16] and even vein pulsation patterns [17] were also introduced for feature representation. In order to minimize the impact of the background as much as possible, these methods should accurately strip out the veins from the whole image. However, owning to the unexpected low quality of the acquired FV image, it has always been a great challenge to screen out the vessels accurately, while either over-segmentation or under-segmentation is the actual situation [18]. The “vein-level” features depend on pure and accurate vein pattern extraction, while neglecting the spatial relationship between veins and their surrounding subcutaneous tissues. As claimed in [19], the optical characteristics such as absorption and scattering in those non-vein regions were also helpful for recognition. Following this research line, another kind of method, namely “image-level” [5], aimed at extracting features from the whole image, while not distinguishing vein and non-vein regions. Among these, some local-pattern-based image features (e.g., local line binary pattern (LLBP) [20,21], local directional code (LDC) [22], discriminative binary code (DBC) [23]) have been widely adopted. Accompanying this, subspace-learning-based global image feature approaches, such as PCA [24,25] and LDA [26], have also been applied. Furthermore, such local and global features have been integrated to construct more-compact and -discriminative FV features [27].
The design of the aforementioned hand-crafted features usually depends on expert knowledge and lacks generalization over various FV imaging scenarios. Admittedly, these methods always rely on many preprocessing strategies to solve problems such as finger position bias, uneven illumination, etc. Relatively speaking, learning-based methods can provide more-adaptive feature representation, especially for the convolutional neural network (CNN)-based deep learning (DL) methods, which adopt a multi-layer nonlinear learning process to capture high-level abstract features from images [28,29,30]. Currently, CNNs equipped with various topological structures have been migrated to FV biometrics and have obtained commendable success. Among these, a deep CNN, namely “DeepVein” [31], was constructed based on the classic VGG-Net [32]. In [33], AlexNet was directly transferred to FV identification. In [34], convolutional kernels with smooth line shapes were especially picked out from the first layer of AlexNet and used to construct a local descriptor, namely the “Competitive Order”. In [35], multimodal biometrics, including finger veins and finger shape, were extracted from ResNet [36], respectively, and then fused for individual identity authentication. In [37], two FV images were synthesized as the input to DenseNet [38], while in [39], vein shape feature maps and texture feature maps were input into DenseNet in sequence and then fused for FV recognition. It must be conceded that DenseNet, due to its dense connection mechanism, generally has higher training complexity than AlexNet, VGG-Net, and ResNet [40].
The above classic DL models mostly adopt a data-driven feature-learning process, and their learning ability primarily relies on the quantity and quality of available image samples [41]. However, this is unrealistic in the FV community as most publicly available FV datasets are small-scale [42]. To address this issue, some fine-tuning strategies [43] and data augmentation technologies have been introduced to make up for the samples shortage to some extent. On the other hand, since vein images generally contain some low-level and mid-level features (mainly textures and shape structures), wider networks rather than deeper ones are preferred to learn a variety of relatively shallow semantic representations. In this regard, model distillation and lightweight models are also exploited for FV identity discrimination. In [44], a lightweight DL framework with two channels was exploited and verified on a subject-dependent FV dataset. In [45], a lightweight network with three convolution and pooling blocks, as well as two fully connected layers was constructed, and a joint function of the center loss and Softmax loss was designed to pursue highly discriminative features. In [46], a lightweight network, which consisted of a stem block and a stage block, was built for FV recognition and matching; the stem block adopted two pathways to extract multi-scale features, respectively, and then, the extracted two-way features were fused and input into the stage block for more-refined processing. In [47], a pre-trained Xception network was introduced for FV classification; due to depthwise separable convolution, the Xception network obtained a lighter architecture; meanwhile, the residual skip connection further widened the network and accelerated the convergence. These lightweight deep networks greatly lessen the training cost while ensuring accuracy, thus being more suitable for real-time applications of the FV trait.
Recently, some more-powerful network architectures have been used for FV recognition tasks, such as the capsule network [48], the convolutional autoencoder [49], the fully convolutional network [50], the generative adversarial network [51], the long short-term memory network [52], the joint attention network [53], the Transformer network [54], the Siamese network [55], etc. Among these, a Siamese framework, which is equipped with two ResNet-50s [36] as the backbone subnetwork, was introduced for FV verification [55]. Compared with some DL networks, which are inclined to learn better feature representation, the Siamese networks tend to learn how to discriminate between different input pairs by using a well-designed contrastive loss function. Therefore, they are more suitable for FV verification tasks, that is they better distinguish between genuine FVs and imposter FVs, rather than obtaining more-accurate semantic expressions. However, although the aforementioned network models have shown a strong feature-learning ability, they have the disadvantages of a complex model structure and an expensive training cost (Table 1).
Table 1. A brief summary of the advantages and disadvantages of existing finger vein verification methods or models.
| Category | Methods/Models | Advantages | Disadvantages | |
|---|---|---|---|---|
| Hand-Crafted | Vein-Level | Point [7,8], Line [10,11] | Pure | Lack Generalization |
| Curvature [12,13,14] | Vein Pattern | |||
| Anatomy [15,16] | Representation | |||
| Vein Pulsation [17] | ||||
| Image-Level | LLBP [20,21] | Do Not Distinguish | ||
| LDC [22] | Vein and Non-Vein | |||
| DBC [23] | Regions | |||
| Learning-Based | Classic Models | DeepVein [31] | ||
| AlexNet [33,34] | Capture High-Level | Complex Network Structures, |
||
| ResNet [36] | Abstract Features | Massive Sample Requirement |
||
| DenseNet [39] | ||||
| Powerful Models | Capsule [48], CAE [49], FCN [50] | |||
| GAN [51], LSTM [52] | Stronger | |||
| Joint Attention Network [53] | Feature | More Complex Network Structures |
||
| Transformer Network [54] | Representations | |||
| Siamese Network [55] | ||||
| Lightweight Models | Two-Stream CNN [44] | Simper Network | ||
| Light CNN [45,46] | Structures, Lower | Feature Representation Is Weak |
||
| Xception [47] | Computation Cost |
2. Basic Procedure of Finger Vein Verification
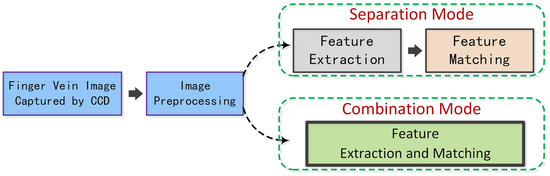
In general, the processing flow of an FV verification system consists of four tasks: image capturing, preprocessing, feature extraction, and feature matching, as shown in Figure 2. Among these, the stages of image preprocessing and feature extraction are the most-critical ones; some preprocessing strategies, such as ROI localization and contrast enhancement, have a significant impact on the subsequent feature extraction. In the meantime, a powerful feature representation ability is key to precise matching.
Figure 2. Illustration of the basic processing flow of a finger vein verification system.
As stated earlier, deep CNNs have shown the capability to learn unprecedentedly efficient image features. However, most of the existing DL models regard feature extraction and feature matching as two separate stages, thus lacking a comprehensive consideration of feature learning from the perspective of discriminant matching. Instead, the Siamese network combines both of these through contrastive learning, so that the learned features can better serve the final matching purposes.
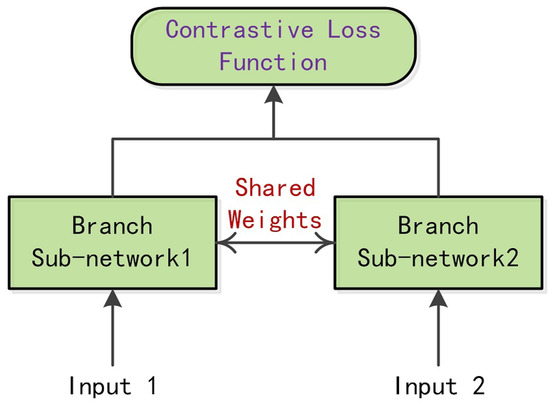
3. Siamese Network Framework
A Siamese network is usually equipped with a pair of subnetworks, as shown in Figure 3. For a pair of input samples, their feature vectors are learned by the corresponding subnetworks and then given to the contrastive loss function for similarity measurement. Generally, the contrastive loss function can be defined by Equation (1).
where 𝐷𝑤 is the similarity distance metric, 𝛾 is an indicator of whether the prediction is from the same finger class, 𝛾 equals 0, otherwise, 𝛾 equals 1, and m is a positive margin value, which is used to protect the loss function from being corrupted when the distance metric of different sample pairs exceeds this margin value.
Figure 3. Illustration of a Siamese network framework.
4. Gabor Convolutional Kernel
The Gabor convolutional kernel represents a combination of classic computer vision and deep neural networks; similar works have proven it to be successful [56]. According to their combination strategies, existing methods can be divided into three categories: The first category regards the Gabor filter as a kind of preprocessing, which means the inputs of the CNNs are Gabor-filtered images. Furthermore, in [57], convolutional kernels in the first two layers of the CNN were replaced by Gabor filters with fixed parameters. In this case, although the parameters of the trainable network were reduced, it still lacked a deep combination of the Gabor filters’ representation ability and the CNN’s learning ability. The second category completely replaces the convolutional kernels with Gabor filters and optimizes the parameters of the Gabor filters. Among these, in [58], only the first layer was replaced by the Gabor filters, while the remaining layers remained unchanged. In [59], a parameterized Gabor convolutional layer was used to replace a few early convolutional layers in the CNNs, and it obtained a consistent boost in accuracy, robustness, as well as highly generalized test performance. However, due to the computational complexity of the Gabor convolution operation and the corresponding parameter optimization algorithm, its popularization has been restricted. The third category adopts Gabor filters to modulate the learnable convolutional kernels [60]. Compared with the above two categories, such a method allows the network to capture more robust features with regard to orientation and scale changes, while not bringing additional computational burden.
This entry is adapted from the peer-reviewed paper 10.3390/math11143190
This entry is offline, you can click here to edit this entry!
