While several developments have taken place in the field of autonomus guidance and navigation techniques for Unmanned Aerial Vehicle (UAV) systems, obtaining an optimal path planning algorithm remains elusive. With multiple UAVs involvement in missions, these difficulties increase significantly leading to the need for collision free navigation routes from the UAVs' initial positions to target points. Consequently, this entry focuses specifically on Multi-UAV Path Planning Algorithms utilizing Bio -Inspired Algorithms. The findings indicated that bio-inspired algorithms possess substantial potential in addressing multipoint path planning issues and delineate new prospects and implications for the enhancement of this active research domain.
- unmanned aerial vehicle
- UAV
- Path Planning
1. Introduction
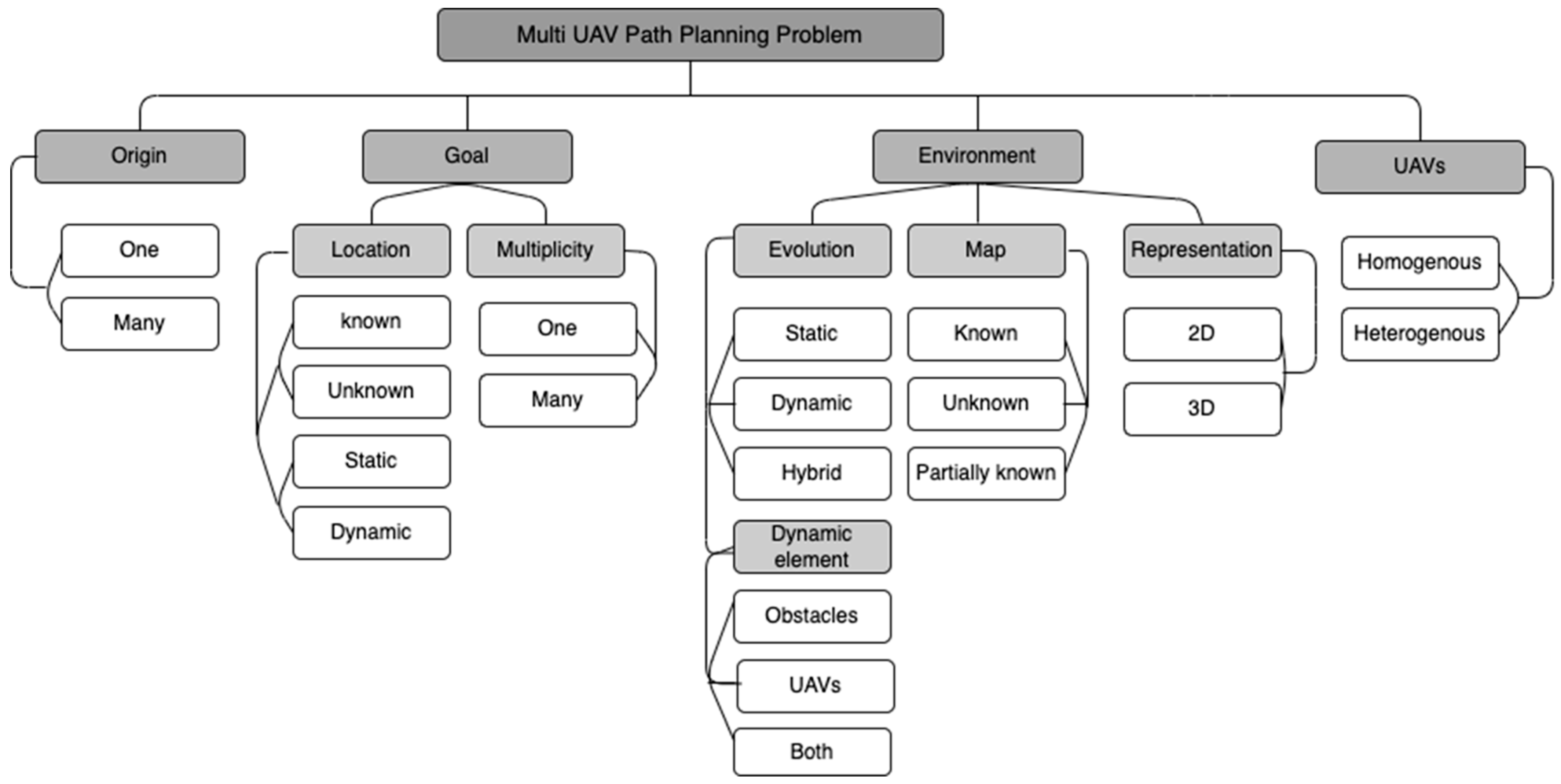
2. The Multi-UAV Path Planning Problem
-
Origin/starting point/source: It is also known as the depot in the traveling salesman problem (TSP) [34][35]. It represents the current location of the UAV or the initial location from where the UAV should start traveling. A path planning problem for a single UAV system usually requires one starting location, however, for a multi-UAV system, there might be a shared starting location or several starting locations.
-
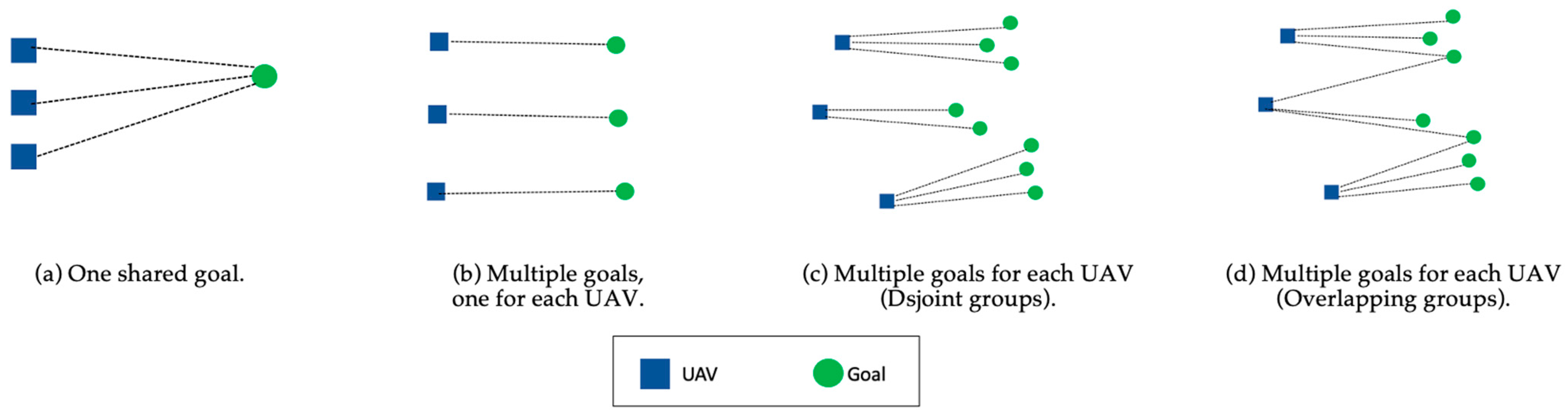
Goal/end point/destination/target: It represents the final location where the UAV should stop. There can be one or more goals. Goals can be known or unknown in advance. They can be static, i.e., stationary throughout the mission, or dynamic. i.e., change their locations over time [4]. The schemes of goals can be one following:
-
One shared goal for all UAVs: There is one goal, and all UAVs will have to visit this goal.
-
Multiple goals, one for each UAV(One-for-each): Each UAV is allowed to visit exactly one goal.
-
Multiple goals for each UAV (Multi-for each): There are multiple sets of goals, and each set can be visited by precisely one UAV. In this case, the sets are assigned at an initial phase for each UAV [24]. or each UAV searches for its goals set [36][37]. Alternatively, sets of goals can be overlapping, as shown in Figure 2.
-
-
UAVs: A multi-UAV system can be composed of homogenous vehicles, i.e., with identical features and capabilities, or heterogeneous vehicles, i.e., with different capabilities [38]. A key feature, especially for a multi-UAV system, is collision avoidance (CA). CA is an important capability when there are obstacles or multiple UAVs in the environment. However, CA adds a layer of complexity and challenges, hence, sometimes it is ignored based on certain assumptions [39]. In 3D environments, in particular, CA is an issue that should be explicitly handled either by an altitude layering approach which means that each UAV flies at a different altitude [40][41], or through a safe distance approach where the distance between any two UAVs should not exceed a safe distance [10].
-
Environment (Env.): It is the workspace in which a UAV navigates which can be embodied in two-dimensional (2D) or three-dimensional (3D) planes. A map representation is usually developed for the environment which can be known, unknown, or partially known [10][42]. A known map accurately represents the environment and encapsulates all of its details, such as the surrounding area and obstacles, while a map with approximate or uncertain information is considered partially known. On the other hand, in an unknown environment, where a UAV can only acquire further knowledge about the surroundings during navigation, the map is considered unknown [43]. Another primary characteristic of the environment affecting path planning problems is its evolution which can be static or dynamic [4]. A static environment comprises unchanging settings while a dynamic environment includes moving objects, usually obstacles or other UAVs [44], which change the environment geometry [45]. Dynamicity of the environment can be handled by either replanning the initial path or calculating the probability of the target position in different cells or time frames. However, replanning the initial path can encounter limitations when certain thresholds have been exceeded, such as in [46][47].
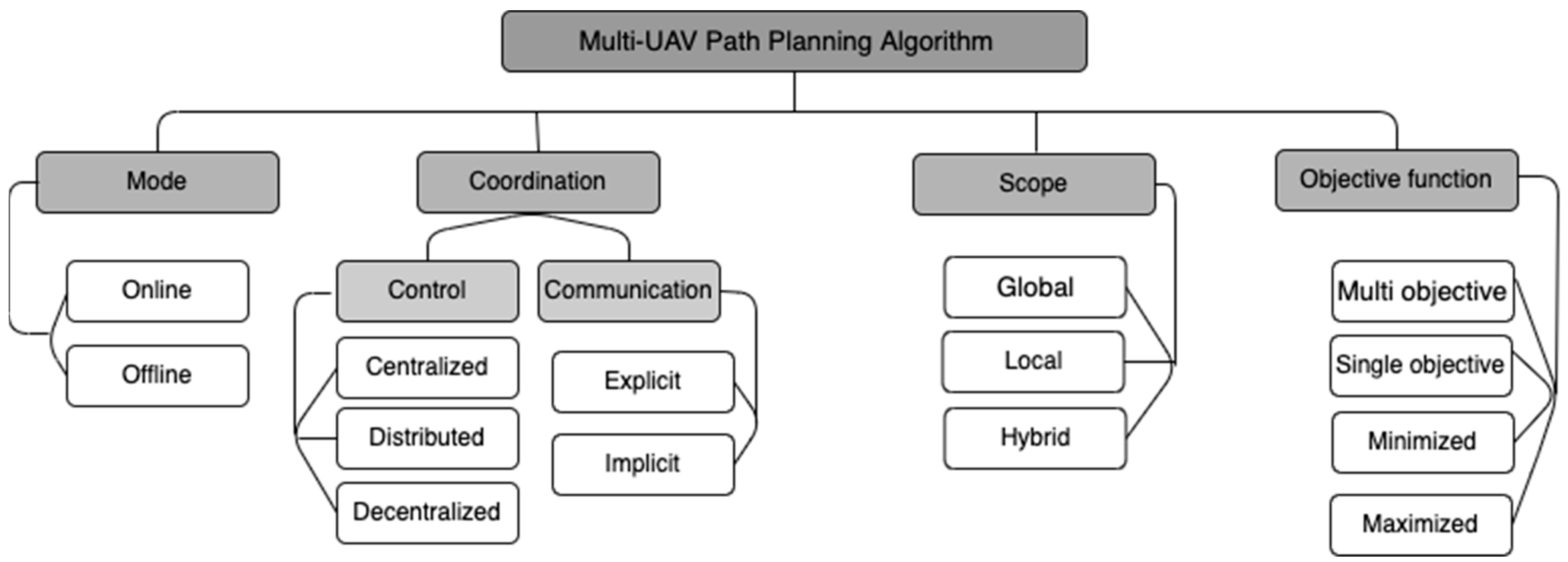
3. Multi-UAV Path Planning Algorithms
-
Mode: The path planning mode can be offline or online. An offline planner constructs the path before motion begins. In contrast, an online planner incrementally constructs the plan while the UAV is in motion [48][49]. Typically, it is recommended to combine the two approaches to maximize their strengths [17].
-
Coordination: The coordination process in a multi-UAV system describes the control structure and communications scheme between the vehicles.
-
Control can occur in a centralized or decentralized manner [50][51]. In centralized planning approaches, a single control agent acts as a leader to ensure coordination among the entire team of UAVs [18][51]. This central agent (e.g., a control station) usually has global knowledge about network status and each robot’s interactions [18][50]. Decentralized architectures can be further divided into distributed architectures and hierarchical architectures. In hierarchical coordination, multiple-leader robots operate as central nodes for smaller groups of robots. Then, each leader coordinates with other leaders’ space [50][52].
-
On the other hand, distributed approaches lack a central agent; instead, the individual agents plan and adjust their paths. The decisions are distributed on the robot team’s side, not determined by a base station [18][51][52][53]. Hence, distributed systems are more robust and fault-tolerant than centralized approaches [18]. Specific applications follow a hybrid approach to leverage the advantages of both centralized and distributed methods [53].
-
It is worth noting that the terms decentralized and distributed are used interchangeably in the literature (e.g., the study [53]), although referring to distinct elements of the decision-making policy of the system: authority and responsibility. As a result, we can have a decentralized system in which the responsibility is not distributed equally but in a hierarchal scheme, as illustrated before.
-
Communications allow sharing of information between robots to enhance their perception of the environment and inform the decision-making required for motion planning [4]. Communications can be categorized based on how the robots exchange information to direct/explicit and indirect/implicit communications. In explicit communications, robots share information directly, which might take the form of unicast or broadcast messages, while in implicit communications a robot learns about other robots in the system by observing its environment [50].
-
-
Scope: Based on the information scale considered while generating the path, planners can be classified as global, local, or hybrid/mixed [19][48]. If information about the entire environment is used to plan the path, the planners are considered global. Global planners are known for their efficiency when the environment map is perfectly known and the environment is static, therefore, they are also known as static planners. In contrast, local path planners only consider the area surrounding the vehicle, they are essential when no environment map is available or when the environment is dynamic, thus they are known as dynamic or reactive planners [3][4][8][9][42]. In hybrid path planning, both types are used together; a local planner takes the path from a global planner and then dynamically adjusts it according to obstacles in the environment [54].
-
Objective function: An optimization criterion that is defined by the objective function is required for finding a path. An objective function can be a multi-objective, single-objective, or single-objective with weights (where multi-objective weights are balanced and transformed to single-objective weights) function that should be maximized or maximized [55]. There are many standard optimization objectives in cooperative path planning, and the common ones: are cost minimization, payoff optimization, performance optimization, and risk minimization, such as threats or flight altitude. The objective function may have different formulations in different scenarios [10].
This entry is adapted from the peer-reviewed paper 10.3390/math11102356
References
- Kurdi, H.; AlDaood, M.F.; Al-Megren, S.; Aloboud, E.; Aldawood, A.S.; Youcef-Toumi, K. Adaptive task allocation for multi-UAV systems based on bacteria foraging behaviour. Appl. Soft Comput. 2019, 83, 105643.
- Boukoberine, M.N.; Zhou, Z.; Benbouzid, M. A critical review on unmanned aerial vehicles power supply and energy management: Solutions, strategies, and prospects. Appl. Energy 2019, 255, 113823.
- Kurdi, H.A.; Aloboud, E.; Alalwan, M.; Alhassan, S.; Alotaibi, E.; Bautista, G.; How, J.P. Autonomous task allocation for multi-UAV systems based on the locust elastic behavior. Appl. Soft Comput. 2018, 71, 110–126.
- Khan, A.; Rinner, B.; Cavallaro, A. Cooperative robots to observe moving targets: A review. IEEE Trans. Cybern. 2016, 12, 187–198.
- Parker, L.E. Path Planning and Motion Coordination in Multiple Mobile Robot Teams. Encycl. Complex. Syst. Sci. 2009, 24, 5783–5800.
- Zhang, D.; Duan, H. Social-class pigeon-inspired optimization and time stamp segmentation for multi-UAV cooperative path planning. Neurocomputing 2018, 313, 229–246.
- Basiri, A.; Mariani, V.; Silano, G.; Aatif, M.; Iannelli, L.; Glielmo, L. A survey on the application of path-planning algorithms for multi-rotor UAVs in precision agriculture. J. Navig. 2022, 75, 364–383.
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299.
- Patle, B.K.; Babu, L.G.; Pandey, A.; Parhi, D.R.K.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606.
- Zhang, H.; Xin, B.; Dou, L.; Chen, J.; Hirota, K. A review of cooperative path planning of an unmanned aerial vehicle group. Front. Inf. Technol. Electron. Eng. 2020, 21, 1671–1694.
- Zhao, Y.; Zheng, Z.; Liu, Y. Survey on computational-intelligence-based UAV path planning. Knowl. Based Syst. 2018, 158, 54–64.
- Israr, A.; Ali, Z.A.; Alkhammash, E.H.; Jussila, J.J. Optimization Methods Applied to Motion Planning of Unmanned Aerial Vehicles: A Review. Drones 2022, 6, 126.
- Ait Saadi, A.; Soukane, A.; Meraihi, Y.; Benmessaoud Gabis, A.; Mirjalili, S.; Ramdane-Cherif, A. UAV Path Planning Using Optimization Approaches: A Survey. Arch. Comput. Methods Eng. 2022, 29, 4233–4284.
- Del Ser, J.; Osaba, E.; Molina, D.; Yang, X.-S.; Salcedo-Sanz, S.; Camacho, D.; Das, S.; Suganthan, P.N.; Coello Coello, C.A.; Herrera, F. Bio-inspired computation: Where we stand and what’s next. Swarm Evol. Comput. 2019, 48, 220–250.
- Gonzalez, R.; Kloetzer, M.; Mahulea, C. Comparative study of trajectories resulted from cell decomposition path planning approaches. In Proceedings of the 21st International Conference on System Theory, Sinaia, Romania, 19–21 October 2017.
- Orozco-Rosas, U.; Montiel, O.; Sepúlveda, R. Parallel Bacterial Potential Field Algorithm for Path Planning in Mobile Robots: A GPU Implementation. In Fuzzy Logic Augmentation of Neural and Optimization Algorithms: Theoretical Aspects and Real Applications; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2018.
- Mac, T.T.; Copot, C.; Tran, D.T.; De Keyser, R. Heuristic approaches in robot path planning: A survey. Robot. Auton. Syst. 2016, 86, 13–28.
- Koubaa, A.; Bennaceur, H.; Chaari, I.; Trigui, S.; Ammar, A.; Sriti, M.-F.; Alajlan, M.; Cheikhrouhou, O.; Javed, Y. Robot Path Planning and Cooperation; Studies in Computational Intelligence; Springer International Publishing: Cham, Switzerland, 2018; Volume 772, ISBN 978-3-319-77040-6.
- Lamini, C.; Benhlima, S.; Elbekri, A. Genetic Algorithm Based Approach for Autonomous Mobile Robot Path Planning. Procedia Comput. Sci. 2018, 127, 180–189.
- Raja, P. Optimal path planning of mobile robots: A review. Int. J. Phys. Sci. 2012, 7, 1314–1320.
- Zhang, H.; Lin, W.; Chen, A. Path Planning for the Mobile Robot: A Review. Symmetry 2018, 10, 450.
- Tang, B.; Xiang, K.; Pang, M.; Zhanxia, Z. Multi-robot path planning using an improved self-adaptive particle swarm optimization. Int. J. Adv. Robot. Syst. 2020, 17, 172988142093615.
- Turpin, M.; Mohta, K.; Michael, N.; Kumar, V. Goal Assignment and Trajectory Planning for Large Teams of Aerial Robots. In Proceedings of the Robotics: Science and Systems IX, Berlin, Germany, 24–28 June 2013.
- Zhang, L.; Zhu, Y.; Shi, X. A Hierarchical decision-making method with a fuzzy ant colony algorithm for mission planning of multiple uAVs. Information 2020, 11, 226.
- Fan, Y.; Deng, F.; Shi, X. Multi-robot Task Allocation and Path Planning System Design. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 4759–4764.
- Skorobogatov, G.; Barrado, C.; Salamí, E. Multiple UAV Systems: A Survey. Unmanned Syst. 2020, 8, 149–169.
- Oh, H.; Shin, H.-S.; Kim, S.; Tsourdos, A.; White, B.A. Cooperative Mission and Path Planning for a Team of UAVs. In Handbook of Unmanned Aerial Vehicles; Valavanis, K.P., Vachtsevanos, G.J., Eds.; Springer: Dordrecht, The Netherlands, 2015; pp. 1509–1545. ISBN 978-90-481-9706-4.
- Khoufi, I.; Laouiti, A.; Adjih, C. A Survey of Recent Extended Variants of the Traveling Salesman and Vehicle Routing Problems for Unmanned Aerial Vehicles. Drones 2019, 3, 66.
- Gonzalez-Bermejo, S.; Alonso-Linaje, G.; Atchade-Adelomou, P. GPS: A New TSP Formulation for Its Generalizations Type QUBO. Mathematics 2022, 10, 416.
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91.
- Rojas Viloria, D.; Solano-Charris, E.L.; Muñoz-Villamizar, A.; Montoya-Torres, J.R. Unmanned aerial vehicles/drones in vehicle routing problems: A literature review. Int. Trans. Oper. Res. 2021, 28, 1626–1657.
- Li, J.; Liu, H.; Lai, K.K.; Ram, B. Vehicle and UAV Collaborative Delivery Path Optimization Model. Mathematics 2022, 10, 3744.
- Raivi, A.M.; Huda, S.M.A.; Alam, M.M.; Moh, S. Drone Routing for Drone-Based Delivery Systems: A Review of Trajectory Planning, Charging, and Security. Sensors 2023, 23, 1463.
- Corberán, Á.; Eglese, R.; Hasle, G.; Plana, I.; Sanchis, J.M. Arc Routing Problems: A Review of the Past, Present, and Future; Wiley Online Library: Hoboken, NJ, USA, 2020.
- Hong, Y.; Jung, S.; Kim, S.; Cha, J. Autonomous mission of multi-UAV for optimal area coverage. Sensors 2021, 21, 2482.
- Ergezer, H.; Leblebicioğlu, K. 3D Path Planning for Multiple UAVs for Maximum Information Collection. J. Intell. Robot. Syst. 2014, 73, 737–762.
- Hu, X.; Liu, Y.; Wang, G. Optimal search for moving targets with sensing capabilities using multiple UAVs. J. Syst. Eng. Electron. 2017, 28, 526–535.
- Sultan, L.; Anjum, M.; Rehman, M.; Murawwat, S.; Kosar, H. Communication among Heterogeneous Unmanned Aerial Vehicles (UAVs): Classification, Trends, and Analysis. IEEE Access 2021, 9, 118815–118836.
- Elmeseiry, N.; Alshaer, N.; Ismail, T. A Detailed Survey and Future Directions of Unmanned Aerial Vehicles (UAVs) with Potential Applications. Aerospace 2021, 8, 363.
- Wu, F.; Varadharajan, V.S.; Beltrame, G. Collision-aware Task Assignment for Multi-Robot Systems. arXiv 2019, arXiv:1904.04374.
- Yan, F.; Zhu, X.; Zhou, Z.; Chu, J. A Hierarchical Mission Planning Method for Simultaneous Arrival of Multi-UAV Coalition. Appl. Sci. 2019, 9, 1986.
- Melo, A.G.; Pinto, M.F.; Marcato, A.L.M.; Honório, L.M.; Coelho, F.O. Dynamic Optimization and Heuristics Based Online Coverage Path Planning in 3D Environment for UAVs. Sensors 2021, 21, 1108.
- Zear, A.; Ranga, V. Path Planning of Unmanned aerial Vehicles: Current state and future challenges. In First International Conference on Sustainable Technologies for Computational Intelligence; Luhach, A.K., Kosa, J.A., Poonia, R.C., Gao, X.-Z., Singh, D., Eds.; Advances in Intelligent Systems and Computing; Springer: Singapore, 2020; Volume 1045, pp. 409–419. ISBN 9789811500282.
- Nazarahari, M.; Khanmirza, E.; Doostie, S. Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm. Expert Syst. Appl. 2019, 115, 106–120.
- Mohanan, M.G.; Salgoankar, A. A survey of robotic motion planning in dynamic environments. Robot. Auton. Syst. 2018, 100, 171–185.
- Shen, L.; Wang, Y.; Liu, K.; Yang, Z.; Shi, X.; Yang, X.; Jing, K. Synergistic path planning of multi-UAVs for air pollution detection of ships in ports. Transp. Res. Part E-Logist. Transp. Rev. 2020, 144, 102128.
- Duan, H.; Zhao, J.; Deng, Y.; Shi, Y.; Ding, X. Dynamic Discrete Pigeon-Inspired Optimization for Multi-UAV Cooperative Search-Attack Mission Planning. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 706–720.
- Ghandi, S.; Masehian, E. Review and taxonomies of assembly and disassembly path planning problems and approaches. Comput.-Aided Des. 2015, 67–68, 58–86.
- Carbone, G.; Gomez-Bravo, F. Motion and Operation Planning of Robotic Systems; Springer International Publishing: Cham, Switzerland, 2015.
- Yan, Z.; Jouandeau, N.; Cherif, A.A. A Survey and Analysis of Multi-Robot Coordination. Int. J. Adv. Robot. Syst. 2013, 10, 399.
- Sarno, S.; D’Errico, M.; Guo, J.; Gill, E. Path planning and guidance algorithms for SAR formation reconfiguration: Comparison between centralized and decentralized approaches. Acta Astronaut. 2020, 167, 404–417.
- Kahng, A.B.; Meng, F. Cooperative Mobile Robotics: Antecedents and Directions. Auton. Robots 1997, 4, 7–27.
- Hilmi Ismail, Z.; Sariff, N. A Survey and Analysis of Cooperative Multi-Agent Robot Systems: Challenges and Directions. In Applications of Mobile Robots; Gorrostieta Hurtado, E., Ed.; IntechOpen: London, UK, 2019; ISBN 978-1-78985-755-9.
- Garrido, S.; Moreno, L.; Gómez, J.V. Motion Planning Using Fast Marching Squared Method. In Motion and Operation Planning of Robotic Systems; Carbone, G., Gomez-Bravo, F., Eds.; Mechanisms and Machine Science; Springer International Publishing: Cham, Switzerland, 2015; Volume 29, pp. 223–248. ISBN 978-3-319-14704-8.
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5, 1502242.
