Sensor Applications of Forward Brillouin Scattering: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Lindsay Dong and Version 3 by Lindsay Dong.

In-fiber opto-mechanics based on forward Brillouin scattering enables sensing the surrounding of the optical fiber. Optical fiber transverse acoustic resonances are sensitive to both the inner properties of the optical fiber and the external medium. A particularly efficient pump and probe technique—assisted by a fiber grating—can be exploited for the development of point sensors of only a few centimeters in length. When measuring the acoustic resonances, this technique provides the narrowest reported linewidths and a signal-to-noise ratio better than 40 dB. The longitudinal and transverse acoustic velocities—normalized with the fiber radius—can be determined with a relative error lower than 10−4, exploiting the derivation of accurate asymptotic expressions for the resonant frequencies. 

  • forward Brillouin scattering
  • opto-mechanics
  • acoustic transverse resonances
  • temperature ans strain sensors
  • Poisson's ratio

1. Introduction

The study of forward Brillouin scattering (FBS) in optical fibers, i.e., forward scattering of a guided optical wave by transverse acoustic resonances of the fiber itself, started in the 1980s [1] and is attracting increasing interest in recent years [2]. Early studies employed optical heterodyne detection to resolve the fine structure of thermally excited acoustic modes. Since then, continuous improvements in the excitation and detection approaches have impelled both fundamental studies and sensor applications. Preferable excitation schemes use either a simple optical pulse to excite a broadband of acoustic frequencies simultaneously [3], or a dual-frequency laser source for the selective excitation of acoustic resonances matching the frequency difference [4]. In both cases, electrostriction is the dominant physical effect responsible for the optical excitation of transverse acoustic resonances. Although heterodyne detection is always an option [5], detection has been carried out frequently using a Sagnac interferometer driven by an auxiliary probe signal.
The idea of emulating the success of distributed fiber sensing based on backward Brillouin scattering has driven some recent developments, bearing in mind that FBS would enable measuring properties of the fiber surrounding. The need for removing the coating of a standard optical fiber is certainly a severe drawback for practical applications of distributed sensors [6][7]. Typically, only some sections of the fiber are uncoated, and the reported spatial resolutions are higher than 2 m. One approach to overcome this limitation is the use of optical fibers coated with a thin layer of polyimide, since the mechanical properties of this material significantly reduce the attenuation of acoustic waves in silica fibers [8][9]. Thus, it is possible to distinguish between air, water, and ethanol outside a fiber coated with polyimide [10], with a reported resolution of 50 m. It is worth mentioning that FBS has been demonstrated to be a useful tool for the characterization of elastic properties of fiber coatings [11].

2. A Point Pump and Probe Technique

Sensor applications based on FBS would appear to be doomed to large spatial resolutions of the order of meters. Thus, sensing liquids with a simple drop would be beyond the achievable. The development of point sensors in which the physical mechanism for sensing the external medium is the acoustic field, but not the optical field, can give rise to a range of applications parallel and complementary to the more conventional fiber sensors based on optical mechanisms.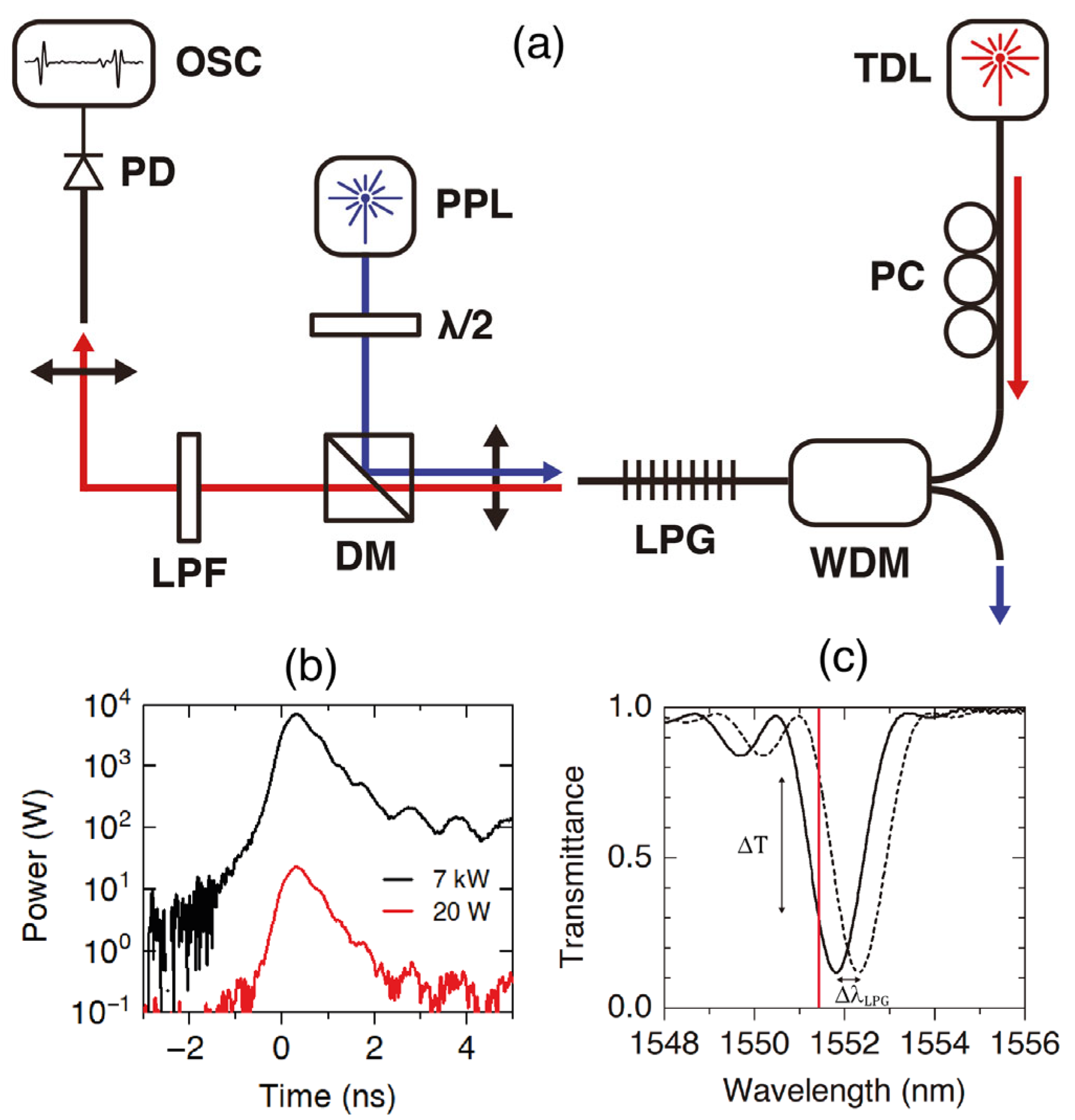
Figure 1a depicts the pump and probe technique. The fiber under test (FUT) has about 20 cm length and the coating was removed for two reasons, first for writing the LPG and second to have acoustic resonances with the highest possible quality factor. The FUT length could be as short as the length of the long-period grating (LPG) (typically 10 cm). The LPG is critical for the right implementation of the technique. Since the refractive index modulation produced by the acoustic resonances can be extremely small, the LPG needs to have sharp edges to generate the highest possible transmittance modulation with small core refractive index perturbations. Thus, narrow-linewidth LPGs are required. The LPG was fabricated following a technique previously developed [12], that permits the fabrication of 1 nm bandwidth LPGs. More specifically, a high numerical aperture fiber supplied by Fibercore (SM1500-4.2/125, NA 0.29, cutoff wavelength 1387 nm) was used. The period of the grating was Λ = 52.3 μm, the length was L = 11 cm, and the notch wavelength was λLPG = 1551 nm. The 3 dB bandwidth of the LPG was 1.3 nm and the depth of the transmittance at the resonance wavelength was −9 dB.
/media/item_content/202302/63eee915b6879sensors-23-00318-g001.png
Figure 1. (a) Experimental setup. OSC: oscilloscope; PD: fast photodetector; LPF: long-pass filter; DM: dichroic mirror; WDM: wavelength division multiplexer; PPL: pulsed pump laser; λ/2: half wavelength plate; TDL: tunable continuous wave diode laser; PC: polarization controller; Blue line: pump laser path; Red line: probe laser path. (b) Typical pump pulses for 7 kW and 20 W peak powers. (c) Transmittance of the LPG and operation principle of the pump and probe technique: (i) the vertical dashed line indicates the probe laser wavelength, which is set in the linear region of the LPG transmittance, and (ii) the acoustic wave will shift the resonance wavelength of the grating (ΔλLPG) and this will cause the transmission of the probe signal to be modulated by ΔT.
Figure 1b includes oscilloscope traces of the pump pulses for 7 kW and 20 W peak powers (700 ps pulse duration, 1064 nm wavelength, 19.9 kHz repetition rate). Selecting pump pulses of about 1 ns duration ensures an efficient excitation—via electrostriction [13]—of transverse acoustic resonances of hundreds of MHz. Radial resonances of order 6–8 at around 300 MHz exhibit the highest overlap with the fiber core and generate the highest modulation of the core refractive index [14]. Figure 1c includes the transmittance spectrum of the LPG and shows how a small shift of the grating will modulate the probe signal adjusted to the edge of the LPG. The experimental values of the slopes at the central point of the edges—where the slope is linear, s = ∂T/∂λ—are s = −0.98 nm−1 for the left side of the notch and s = 0.90 nm−1 for the right side. It can estimate the relations between a small change of the core effective refractive index (δnco), a given shift of the LPG grating (δλLPG), and a measured change of the transmittance of the probe signal (δT), with the expressions: δ λ L P G = Λ δ n c o   ,       δ n c o = δ T s   Λ   . Figure 2 shows two representative oscilloscope traces of the probe signal modulated by the acoustic waves generated with pump pulses of 7 kW and 20 W peak power, and both traces are the average of 1064 pump pulses. These plots include, on the right-hand side, the calculated effective refractive index change according to Equation (1). Figure 2b shows that effective index changes as small as 10−9 can be detected. The repetition frequency of the pump laser is 19 kHz—52.6 μs period—while damping of the acoustic signal, according to the oscilloscope traces, takes about 1 μs. Thus, it can ensure that the responses of two consecutive pulses are independent of each other.
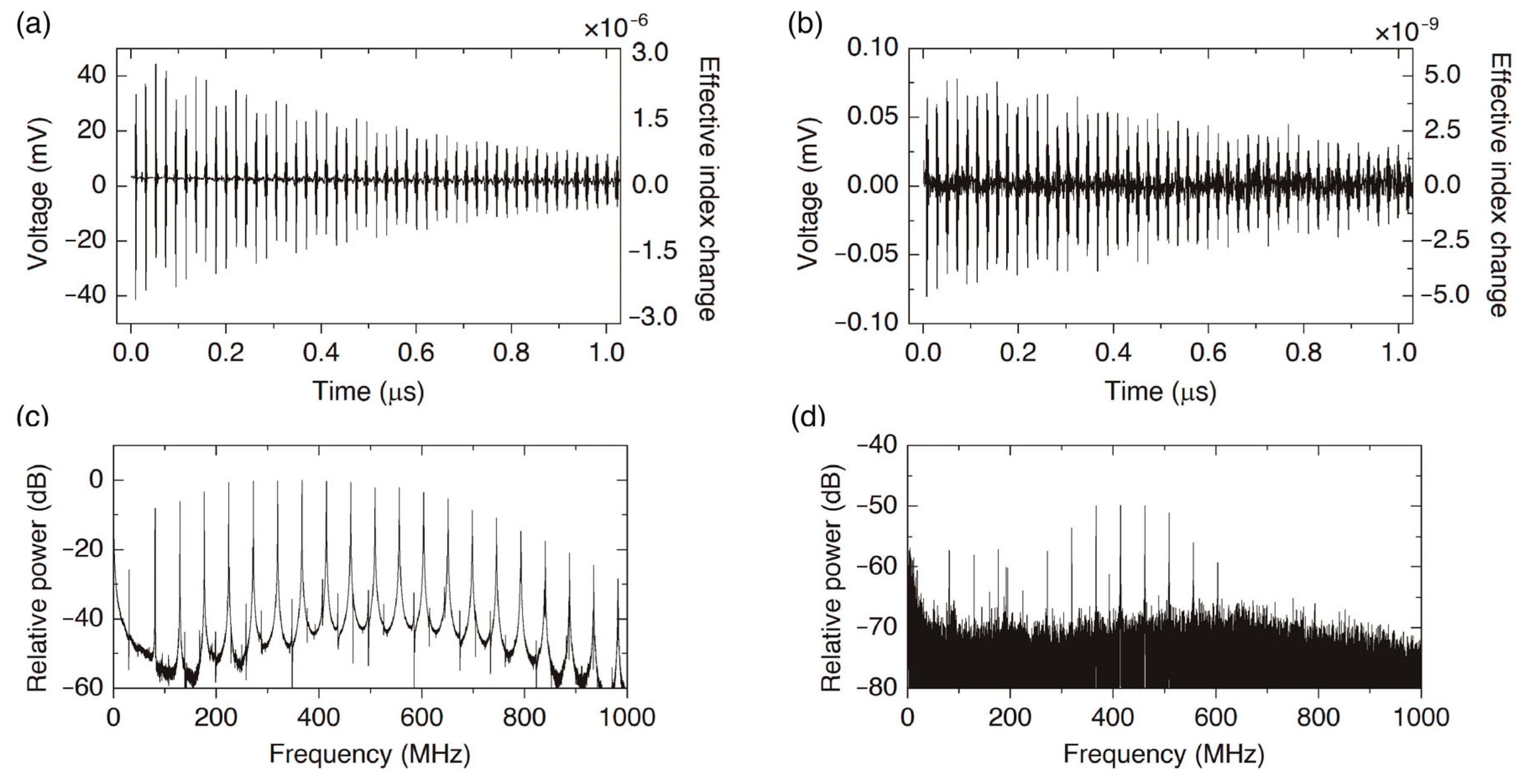
/media/item_content/202302/63eee9479658csensors-23-00318-g002.png
Figure 2. Oscilloscope traces for pump pulses of (a) 7 kW and (b) 20 W. Each one of the traces is the result of 1064 averages. (c,d) The fast Fourier transform of traces (a) and (b): SNR > 40 dB and 15 dB can be observed, respectively, for the strongest resonances.
In addition to a good SNR, the present technique provides the narrowest reported linewidths for the transverse acoustic resonances. The series of resonances observed in Figure 3 are the radial resonances, R0,m. Accurate measurement of each resonance with a RF signal analyzer permits to determine its linewidth. Figure 3 shows the spectra of resonances R0,5 and R0,10—experimental points and fitted Breit–Wigner–Fano function—and the linewidth of R0,m modes versus their resonance frequencies. 
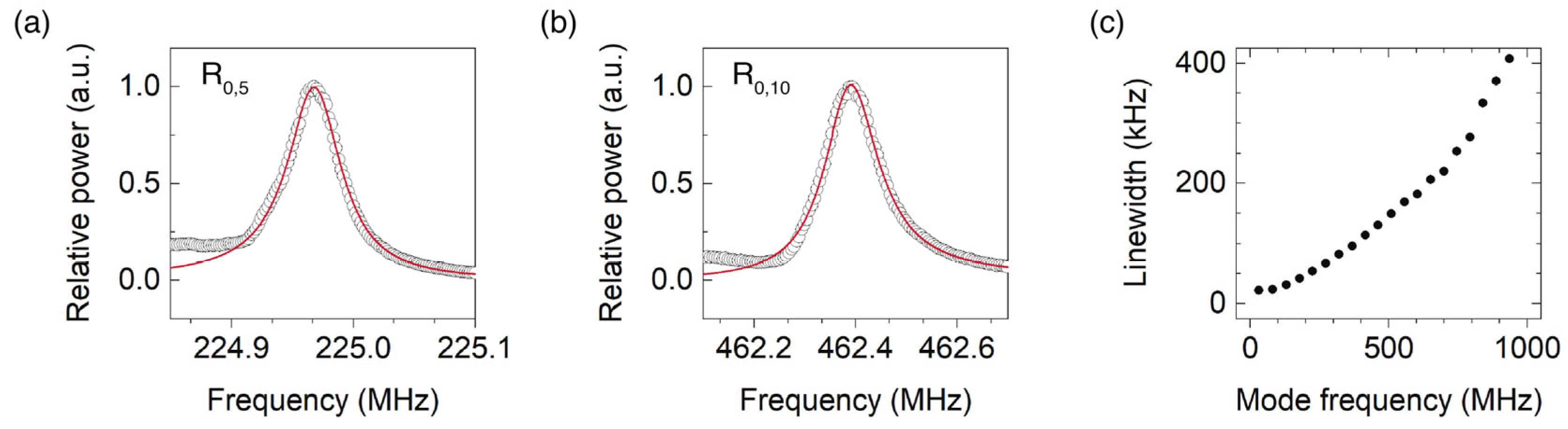
/media/item_content/202302/63eee958e0427sensors-23-00318-g003.png
Figure 3. Acoustic resonances (a) R0,5 and (b) R0,10—experimental points and fitted Breit–Wigner–Fano functions—and (c) linewidth of R0,m resonances versus the frequency.

3. Asymptotic Expressions for High-Order Resonances

The characteristic equations for R0,m and TR2,m resonances are:

R 0 , m   resonances :   1 − α 2 J 0 α z − α 2 J 2 α z = 0   ,

TR 2 , m   resonances :   3 − z 2 / 2 J 2 α z 6 − z 2 / 2 J 2 z − 3 z   J 3 z   J 2 α z − α z   J 3 α z 2 − z 2 / 2 J 2 z + z   J 3 z = 0   ,

where z is the normalized frequency given by z = 2πa f /VS, and α = VS/VL, with f being the frequency, a the fiber radius, VS and VL the shear and longitudinal acoustic wave velocities, and Jm the Bessel functions of the first kind of order, m.

Having in mind the idea of extracting the information from the whole spectrum of acoustic resonances, better than from one or two resonances, as it is usual in sensor applications developed so far, we found it very useful to derive accurate asymptotic expressions for the resonance frequencies determined by Equations (2) and (3). Using Hankel’s asymptotic expansions of Bessel functions for large arguments [15], and following the procedure outlined in [16]:
R 0 , m resonances : f R , m = V L 2 π a c m − 16 α 2 − 1 8 c m ,
TR 2 , m 1   resonances :   f T R , m 1 = V S 2 π a c m + 1 − 15 8 c m + 1   ,
TR 2 , m 2   resonances :   f T R , m 2 = V L 2 π a c m + 1 − 15 8 c m + 1   ,
where c m = m π − π / 4 , m = 1, 2, 3, etc. These expressions retain the first two dominant terms for high-order resonances and provide high-accuracy numerical values for the frequencies of resonances, provided there is no degeneracy between TR 2 , m 1 ,m and TR 2 , m 2 ,m resonances.

4. Sensor Applications

4.1. High-Accuracy Measurement of Poisson’s Ratio

An accurate determination of Poisson’s ratio (ν) of optical fibers is an evasive issue that has been unattainable for many years. A value ranging between 0.16 and 0.17 is assumed, with a relative error of 6% [17][18]. The determination of ν is carried out typically by combining interferometric and polarimetric measurements. Using the pump & probe technique reporterd here and the asymptotic expressions (4) and (5), it is possible to achieve an accuracy improvement of about two orders of magnitude, pushing the relative error down to 10−3. This result proves the potential of the pump and probe approach to develop point sensors based on FBS with low detection limits [19].

4.2. Simultaneous Strain and Temperature Measurement with a Single-Point Sensor

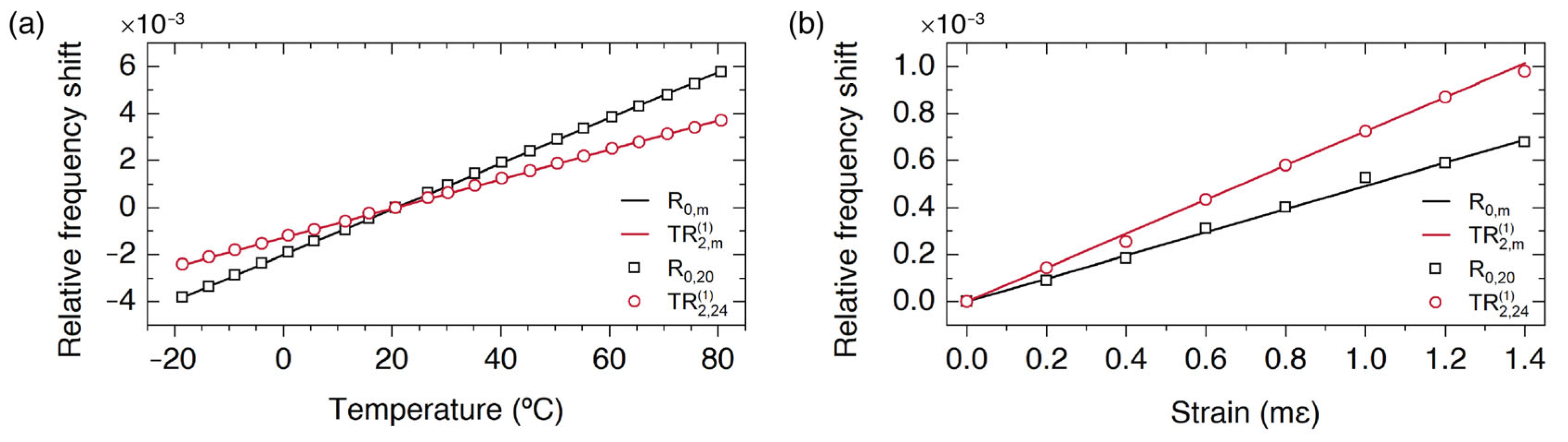
Here, the implementation of simultaneous and discriminative measurements of strain (ε) and temperature using a single-point sensor that exploits the FBS pump and probe technique is discussed. The proposed approach exploits the different sensitivities of radial, R 0 , m , and torsional-radial, TR 2 , m 1 , resonances with strain and temperature, generated by the different temperature and strain coefficients of the longitudinal and shear acoustic wave velocities (∂VL/∂T ≠ ∂VS/∂T and ∂VL/∂ε ≠ ∂VS/∂ε). In addition, for large values of the order m and according to the asymptotic expressions (4) and (5), we found that the relative shift of all the resonance frequencies of radial modes versus temperature and strain, Δ f R , m / f R , m , will be independent of the order m, and the same happens for the relative shift of the torsional-radial resonances,  Δ f T R , m 1 / f T R , m 1   . Thus, instead of measuring only one radial resonance and one torsional-radial resonance, it can be more robust to measure several of them, or even the whole spectrum. Figure 4 shows the relative frequency shift of two specific resonances and the averaged value obtained using the whole spectrum, showing that there is a perfect agreement. From these measurements, one can calibrate the sensor and obtain the temperature and strain coefficients for Δ f R / f R and Δ f T R / f T R defined by the elements c R , T R ε , T of the following 2 × 2 matrix:

Δ f R / f R Δ f T R / f T R = c R ε c R T c T R ε c T R T Δ ε Δ T   .

/media/item_content/202302/63eeec1b9df0asensors-23-00318-g006.png

Figure 4. Relative frequency shift of resonances R 0 , 20 and TR 2 , 24 1 versus temperature (a) and strain (b). Both figures include the averaged values of Δf/f over all the resonances, R 0 , m and TR 2 , m 1 , of each series (solid lines).

References

  1. Shelby, R.M.; Levenson, M.D.; Bayer, P.W. Guided acoustic-wave Brillouin scattering. Phys. Rev. B 1985, 31, 5244–5252.
  2. Zadok, A.; Diamandi, H.H.; London, Y.; Bashan, G. Forward Brillouin Scattering in Standard Optical Fibers: Single-Mode, Polar-ization-Maintaining, and Multi-Core, 1st ed.; Springer: Cham, Switzerland, 2022.
  3. Kang, M.S.; Brenn, A.; Wiederhecker, G.S.; Russell, P.S. Optical excitation and characterization of gigahertz acoustic resonances in optical fiber tapers. Appl. Phys. Lett. 2008, 93, 131110.
  4. Kang, M.S.; Nazarkin, A.; Brenn, A.; Russell, P. Tightly trapped acoustic phonons in photonic crystal fibres as highly nonlinear artificial Raman oscillators. Nat. Phys. 2009, 5, 276–280.
  5. Beugnot, J.-C.; Lebrun, S.; Pauliat, G.; Maillotte, H.; Laude, V.; Sylvestre, T. Brillouin light scattering from surface acoustic waves in a subwavelength-diameter optical fibre. Nat. Commun. 2014, 5, 5242.
  6. Chow, D.M.; Yang, Z.; Soto, M.A.; Thévenaz, L. Distributed forward Brillouin sensor based on local light phase recovery. Nat. Commun. 2018, 9, 2990.
  7. Pang, C.; Hua, Z.; Zhou, D.; Zhang, H.; Chen, L.; Bao, X.; Dong, Y.K. Opto-mechanical time-domain analysis based on coherent forward stimulated Brillouin scattering probing. Optica 2020, 7, 176–184.
  8. Alcusa-Sáez, E.P.; Díez, A.; Rivera-Pérez, E.; Margulis, W.; Norin, L.; Andrés, M.V. Acousto-optic interaction in polyimide coated optical fibers with flexural waves. Opt. Express 2017, 25, 17167–17173.
  9. Diamandi, H.H.; London, Y.; Bashan, G.; Zadok, A. Distributed opto-mechanical analysis of liquids outside standard fibers coated with polyimide. Appl. Phys. Lett. Photonics 2019, 4, 016105.
  10. Bashan, G.; Diamandi, H.H.; London, Y.; Preter, E.; Zadok, A. Optomechanical time-domain reflectometry. Nat. Commun. 2018, 9, 2991.
  11. Diamandi, H.H.; London, Y.; Bashan, G.; Shemer, K.; Zadok, A. Forward Stimulated Brillouin Scattering Analysis of Optical Fibers Coatings. J. Light. Technol. 2021, 39, 1800–1807.
  12. Poveda-Wong, L.; Cruz, J.L.; Delgado-Pinar, M.; Roselló-Mechó, X.; Díez, A.; Andrés, M.V. Fabrication of long period fiber gratings of subnanometric bandwidth. Opt. Lett. 2017, 42, 1265–1268.
  13. Biryukov, A.S.; Sukharev, M.E.; Dianov, E.M. Excitation of sound waves upon propagation of laser pulses in optical fibres. Quantum Electron. 2002, 32, 765–775.
  14. Antman, Y.; Clain, A.; London, Y.; Zadok, A. Optomechanical sensing of liquids outside standard fibers using forward stimulated Brillouin scattering. Optica 2016, 3, 510–516.
  15. Olver, F.W.J. Bessel Functions of integer order. In Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, 10th ed.; Abramowitz, M., Stegun, I.A., Eds.; National Bureau of Standards Applied Mathematics Series No. 55; U.S. Government Printing Office: Washington, DC, USA, 1972; pp. 364–365.
  16. Sánchez, L.A.; Díez, A.; Cruz, J.L.; Andrés, M.V. High accuracy measurement of Poisson’s ratio of optical fibers and its temperature dependence using forward-stimulated Brillouin scattering. Opt. Express 2022, 30, 42–52.
  17. Bertholds, A.; Dandliker, R. Determination of the individual strain-optic coefficients in single-mode optical fibres. J. Light. Technol. 1988, 6, 17–20.
  18. El-Diasty, F. Multiple-beam interferometric determination of Poisson's ratio and strain distribution profiles along the cross section of bent single-mode optical fibers. Appl. Opt. 2000, 39, 3197–3201.
  19. L. A. Sánchez, A. Díez, J. L. Cruz, and M. V. Andrés High accuracy measurement of Poisson’s ratio of optical fibers and its temperature dependence using forward-stimulated Brillouin scattering. Optics Express 2022, 30, 42, https://doi.org/10.1364/OE.442295.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback