The rising demand for electricity, the economic benefits, and the environmental pressures related to the use of fossil fuels are driving electricity generation mostly from renewable energy sources. One of the main challenges in renewable energy generation is uncertainties involved in forecasting, because of the intermittent nature of renewable sources. The demand also varies according to the time of day, the season, the location, the climate, and the availability of resources. Microgrids offer a potential solution for the integration of small-scale renewable energy sources and loads along with energy storage systems and other non-renewable sources. However, intermittent generation and varying demand need to be matched to provide stable power to consumers. Therefore, it is crucial to design an energy management system to effectively manage the energy sources and supply loads for reliable and efficient operation. This paper reviews different techniques proposed in the literature to achieve the objectives of a microgrid energy management system. The benefits of existing energy management systems and their challenges are also discussed. The challenges associated with uncertainties and methods to overcome them are critically reviewed.
- energy management
- forecast uncertainties
- microgrids
- optimization
- renewable energy integrations
1. Introduction
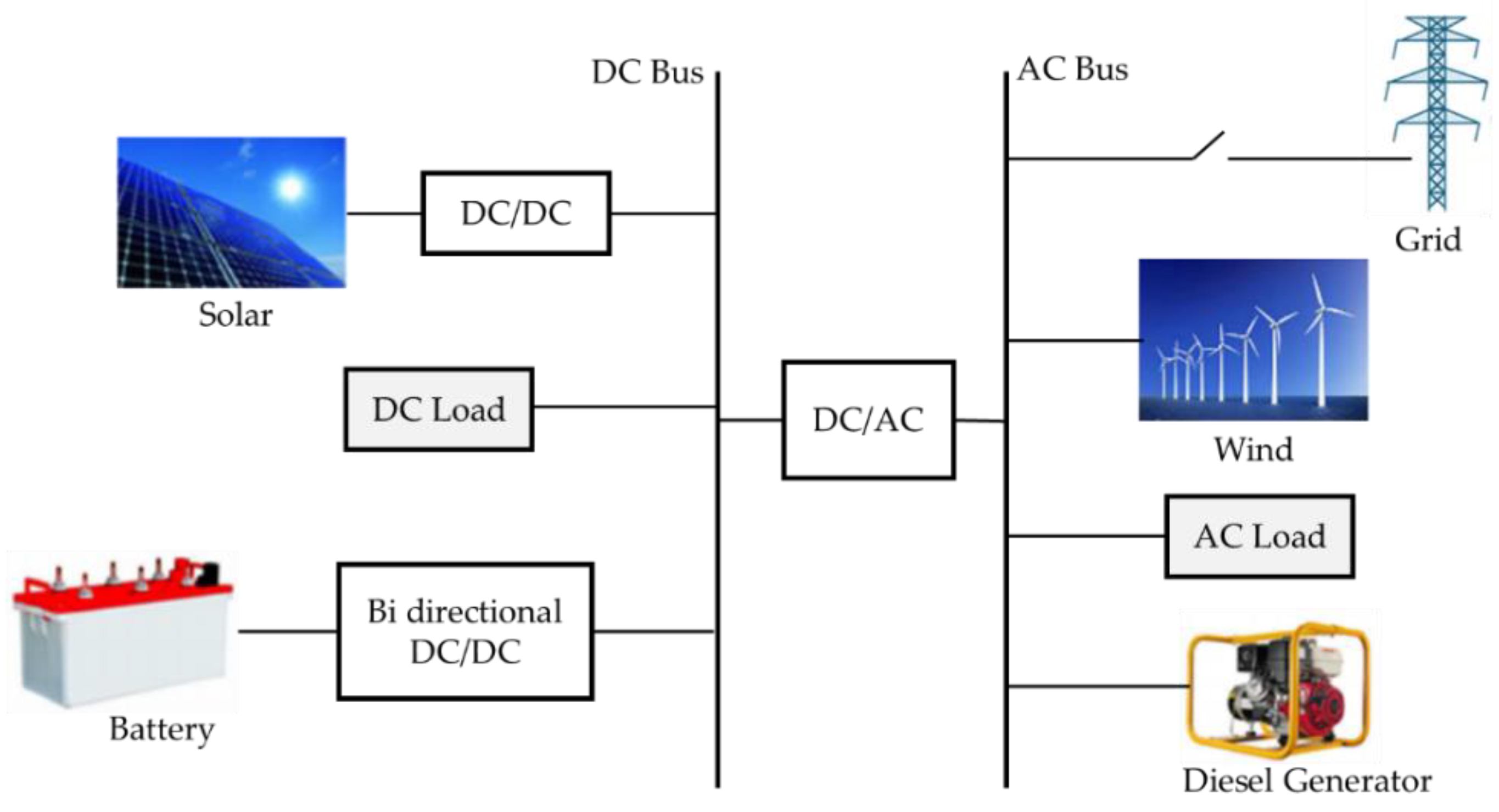
2. Microgrid Energy Management System (MG EMS): The Concept
A microgrid energy management system (MG EMS) performs a variety of functions for the efficient and effective operation of the system. Energy management is an optimization problem with the target of properly scheduling the short-term operation of production by generators, storage, as well as controllable loads, to cover the system demand and minimize the generation costs. The EMS generates a schedule of unit commitment and the optimized output of each source considering the results of the optimization. Figure 2 illustrates the overall outline of the MG EMS.
Control Systems Used in EMS
2.1. Control Systems Used in EMS
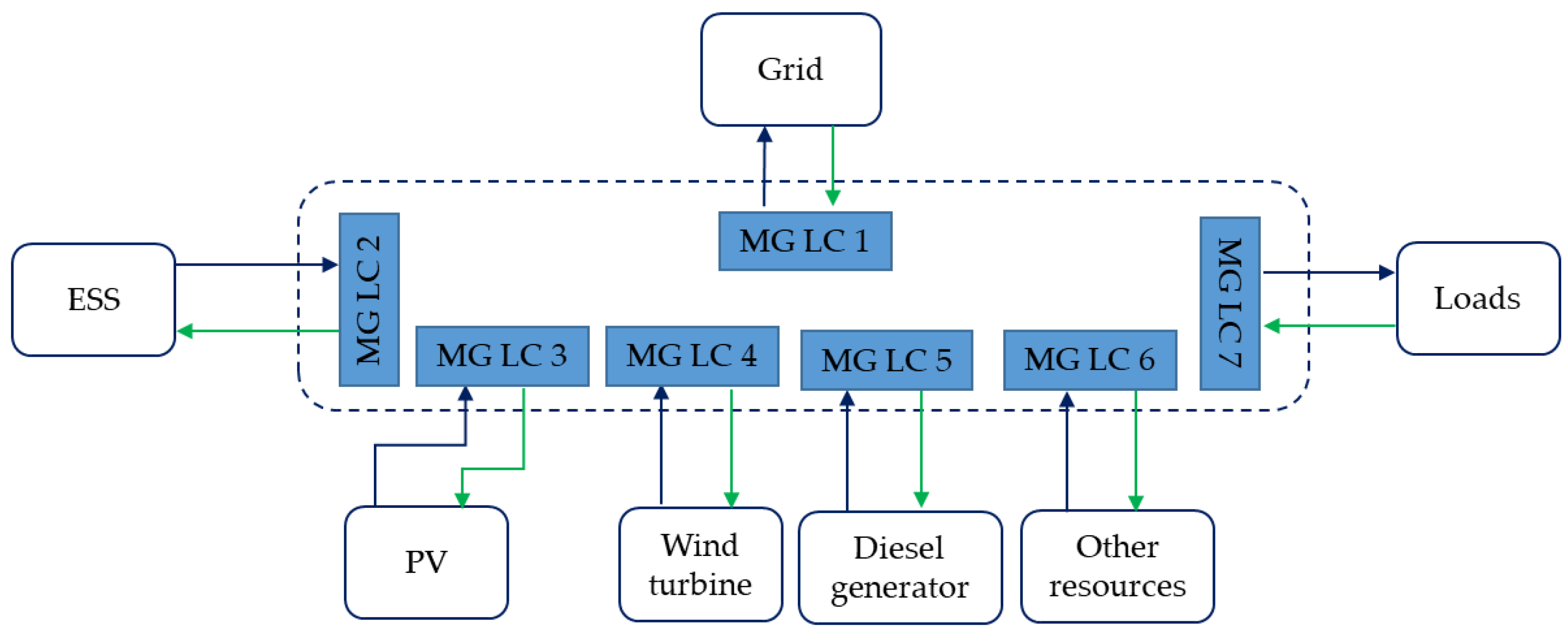
The control system associated with MG EMS can be implemented using centralized, decentralized, and hierarchical control methods [7,15,16][7][15][16]. In centralized control-based EMS, a single central controller that receives all the information, such as RES energy generation, load profile, market price, weather conditions, etc., is used. Based on the inputs, a central controller decides the optimum microgrid energy schedule and then sends these decisions to all local controllers. The basic structure of the centralized control is shown in Figure 3. However, the failure of the central control could cause the entire system to fail. Unlike centralized control-based EMS, in decentralized control shown in Figure 4, a few local connections are needed, and only local measurements are used to make control decisions.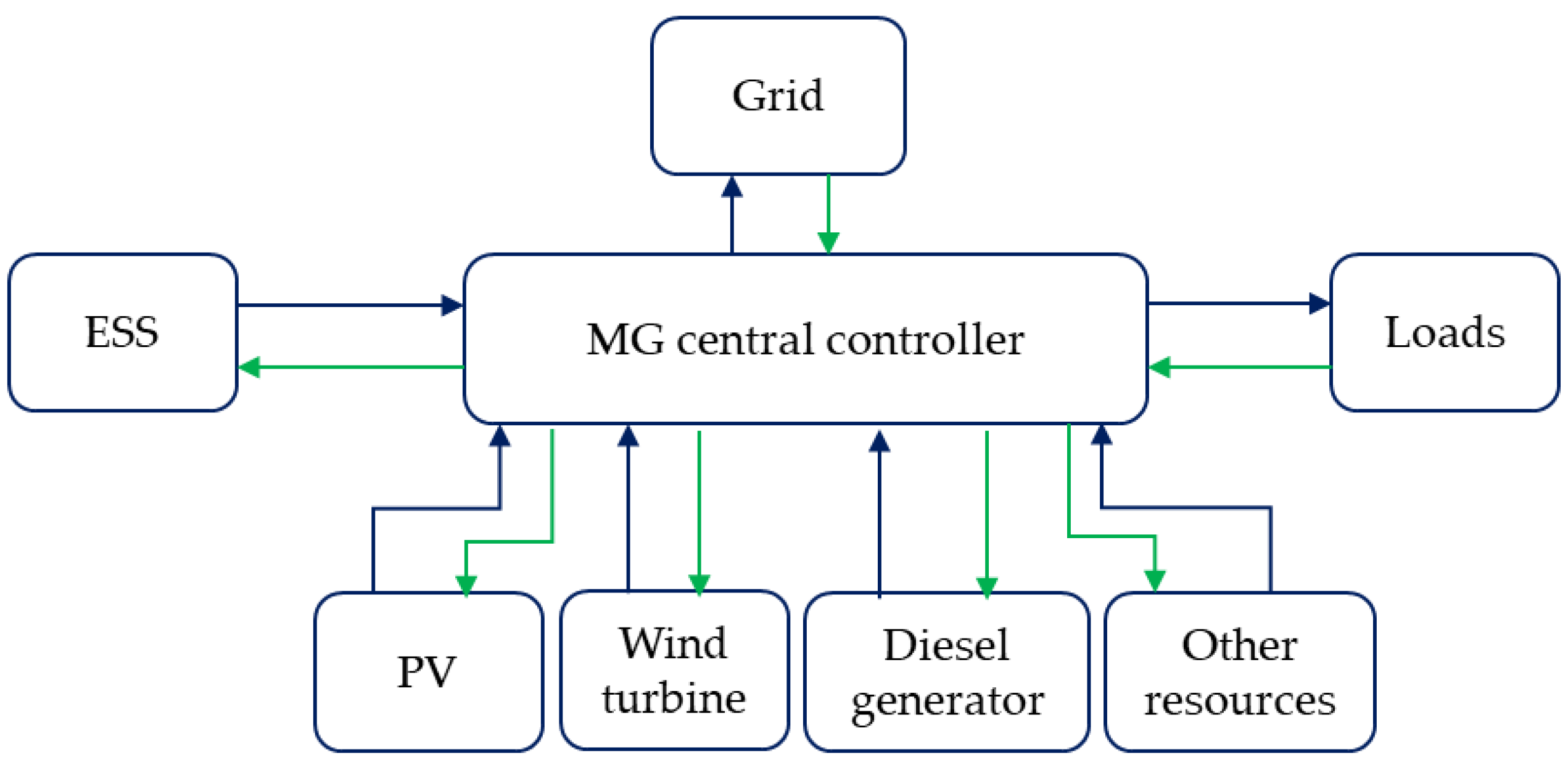

|
Features |
Advantages |
Disadvantages |
|
|---|---|---|---|
|
Centralized control |
Centralized control has complete knowledge of the entire system and is in charge of ensuring its optimal operation. |
It provides wide control over the entire system. Established control approach. Simple architecture. Easy to implement and maintain. It ensures optimal decision. |
It requires a high performance computing unit and communication network. The failure of central control could cause the entire system to fail. Computational complexity is high. Low flexibility. |
|
Decentralized control |
Functions provided by centralized control are realized in a decentralized way. Local decisions contribute to achieving the goal. |
It does not require a high performance computing unit and a high-level connectivity. Easy realization of plug-and-play functionality. |
It requires an effective method to ensure corporation among local controllers. Low performance compared to centralized control due to low response time and incomplete information about the total microgrid system installation. High implementation complexity. |
|
Hierarchical control Based methods |
Each level provides supervisory control over lower-level systems. Three layers: tertiary, secondary, and primary control layers. The bandwidths of different control levels are separated. |
Combining the centralized and decentralized controllers. Higher levels attempt to optimize the microgrid operation. Local controls regulate the voltage and current. It simplifies modelling and analysis of microgrid systems. |
Proper coordination of all three layers is required. |
3. Microgrid Energy Management: Problem Formulation
Microgrid energy management is used to either minimize or maximize an objective or set of objectives while ensuring the constraints of individual units and the system as a whole. These objectives are quantitative in nature and usually include cost reduction, emission reduction, increased renewable energy integration, etc. The associated constraints include power balance, individual unit ratings, charge and discharge rates of ESS, maximum and minimum limits of the state of charge (SOC) of ESS, power import and export limits, and other technical constraints of the microgrid. Most of the existing literature focuses on microgrid cost minimization in a single-objective format. The considered cost factors are related to fuel, start-up, shut-down, maintenance, degradation, utility purchases, etc. When several objectives are optimized, the optimization framework is formulated in a multi-objective framework. In such cases, each objective is assigned a weighting factor. These weighting factors are usually assigned based on the significance of individual objectives in relation to the final objective function. Various solving techniques, such as mixed integer linear and non-linear programming (MILP and MINLP) methods, heuristic optimization methods, etc. are used to solve the optimization problem, sometimes together with rule-based and fuzzy logic control methods to simplify the problem. These optimization strategies use various optimization time windows (horizon) on different time scales. A suitable selection is used to improve the energy management system. Recently, the rolling horizon is considered to reduce the impact of uncertainties from the renewable energy output and load forecasting. The design of an EMS for a microgrid includes the task of the mathematical formulation of objective functions and constraints, selection of the optimization time horizon and the time step, as well as choosing an optimization technique to solve the problem. The typical mathematical representation of the EMS problem is shown below: Objective function: Minimize the total cost of the microgrid operation;-
Operational cost = fuel cost + maintenance cost + startup cost of the thermal unit + shutdown cost of the thermal unit + cost of buying and selling power to the main grid + load shedding penalty cost + losses cost
-
Environmental cost = carbon emission + penalties for emissions
-
Energy storage cost = charging cost + discharging cost + degradation cost
-
Constraints:
-
Power balance: load demand at each time must be equal to the summation of power from microgrid resources and receiving/sending power from the main grid.
-
Emission constraints: emissions caused by each fossil-fueled thermal generators cannot exceed the maximum limits at each time.
-
Capacity limits: each RESs, ESS, and interconnection has a maximum and minimum capacity during the operating mode.
-
Limit of ESS: charging and discharging power rates for batteries during operation mode and the operating SOC range must be limited as it may affect battery life time.
-
Operating reserve: extra storage and generation capacity
-
Generator start/stop limits: the number of generator starts/stops cannot exceed a certain number.
-
Ramp rate power limit: the maximum power fluctuation of each unit is defined.
-
System variables:
-
Load profile: the demand forecast varies according to time, geographical location, season, weather, and other factors.
-
PV and wind sources: the wind and PV power availability depends on wind speed forecasts and solar irradiation forecasts, respectively. Seasonal and local weather impacts these forecasts, and there is always some uncertainty associated with the forecasts.
-
Electricity price: it is related to the price of the buying/selling power to the main grid. Prices may be time-sensitive.
4. Microgrid Energy Management: Solution Approaches
The selection of EMS methods depends on the microgrid system and the requirements. The solution methods for energy management problems can be classified in various ways. Here, those EMS solution methods are classified as shown in Figure 6.
5. Uncertainties in Microgrid Energy Management
- a.
-
Monte Carlo Simulation (MCS)The MCS is used to calculate the probabilities of various outcomes in a process that is difficult to forecast because it contains random variables. This method can accurately handle the uncertainty variable. For each input parameter, a sample is generated using its probability density function (PDF), and the sample generation process is repeated for many iterations. Therefore, the method is computationally complex. Most of the studies are focused on developing uncertainty models for PV, wind power, and load demand [12].
- b.
-
Worst Case Scenario MethodEven though it is not a new concept, the worst-case scenario approach is frequently used in recent studies. The worst-case scenario approach restricts the range of the random variables to a set of predetermined uncertainty with defined upper and lower boundaries. Prediction intervals (PIs) are calculated to evaluate the measure of prediction uncertainty. Upper and lower limits are used to define PIs [11].
- c.
-
Point Estimate Method (PEM)The PEM is one of the approximate methods with a low computation burden. The method focuses the statistical data of a random variable on a specific number (K) of points in order to create a connection between input and output variables. Solar radiation and wind speed are treated as two random variables, and the function is developed using power flow equations in [37][21]. In [38][22], PEM is used to determine power exchanges between MGs and evaluates the optimal solutions in terms of accuracy and computational effort.
- d.
-
Fuzzy MethodEach uncertain parameter can be assigned a degree of membership based on fuzzy theory by using membership functions. After a suitable fuzzy membership function is applied to each parameter, the defuzzification will be carried out. The fuzzy method is used to model the uncertainty in forecasting day-head demand in [39][23]. Although uncertainty is handled in fuzzy systems, the issue of randomness is not properly accounted for. Approaches, such as probabilistic fuzzy systems, have been introduced for overcoming this issue [18].
- e.
-
Autoregressive Moving AverageIt is another model used in recent days to model uncertainties from load demand and wind power. The autoregressive moving average model is a combination of auto regression and moving average. This method can be used to forecast future estimates of a variable if historical data of the variable with uncertainty is presented by a time series, such as load demand, wind, etc. A significant amount of historical data, as well as data mining and analysis, are required for developing proper autoregressive models, and the predictions with these models are valid only over a short horizon [11].Other methods, such as kernel density estimation, hyper-heuristics, and two stage scheduling strategy, are also used to model these uncertainties. Each model has its own advantages and disadvantages that determine its application.There are various approaches that could be used to deal with different sources of uncertainty. Generally, optimization under uncertainties can be broadly categorized as stochastic programming [40,41][24][25], robust optimization [42[26][27],43], and other methods, such as model predictive control and chance constrained programming. These methods are implemented as either a single-layered or multi-layered framework.
6. Application of Artificial Intelligence and Machine Learning
The use of machine learning and data-driven techniques for MG energy management is becoming increasingly popular due to the recent development of machine learning (ML) and artificial intelligence (AI), as well as the availability of advanced processing in modern control systems. For example, ML has been introduced as a methodology either for energy management in microgrids or for forecasting weather conditions and loads. A hybrid approach of a nonlinear MPC controller integrating machine learning models is presented in [70][28]. A two-layer ensemble machine learning technique is used to construct a data-driven multi-model wind forecasting system [71][29]. Utilizing the statistically different characteristics of each machine learning algorithm is the focus of this two-layer model. Additionally, many of the heuristic optimization techniques used in MG EMSs are considered under the umbrella of AI. The opportunities for ML extend far beyond forecasting, model improvement, and adaption.
References
- Su, W.; Yuan, Z.; Chow, M.-Y. Microgrid Planning and Operation: Solar Energy and Wind Energy. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010.
- Elsied, M.; Oukaour, A.; Gualous, H.; Hassan, R.; Amin, A. An Advanced Energy Management of Microgrid System Based on Genetic Algorithm. In Proceedings of the IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014.
- Radosavljević, J.; Jevtić, M.; Klimenta, D. Energy and Operation Management of a Microgrid Using Particle Swarm Optimization. Eng. Optim. 2015, 48, 811–830.
- Chen, Y.-K.; Wu, Y.-C.; Song, C.-C.; Chen, Y.-S. Design and Implementation of Energy Management System With Fuzzy Control for DC Microgrid Systems. IEEE Trans. Power Electron. 2012, 28, 1563–1570.
- Mahmoud, M.S.; Rahman, M.S.U.; Sunni, F.M.A.L. Review of Microgrid Architectures—A System of Systems Perspective. IET Renew. Power Gener. 2015, 9, 1064–1078.
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids Energy Management Systems: A Critical Review on Methods, Solutions, and Prospects. Appl. Energy 2018, 222, 1033–1055.
- Arunkumar, A.P.; Kuppusamy, S.; Muthusamy, S.; Pandiyan, S.; Panchal, H.; Nagaiyan, P. An Extensive Review on Energy Management System for Microgrids. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 4203–4228.
- Ali, S.; Zheng, Z.; Aillerie, M.; Sawicki, J.-P.; Péra, M.-C.; Hissel, D. A Review of DC Microgrid Energy Management Systems Dedicated to Residential Applications. Energies 2021, 14, 4308.
- Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; Kamoun, N.E.; Khaidar, M.; Zine-Dine, K. Review of Control and Energy Management Approaches in Micro-Grid Systems. Energies 2020, 14, 168.
- Shayeghi, H.; Shahryari, E.; Moradzadeh, M.; Siano, P. A Survey on Microgrid Energy Management Considering Flexible Energy Sources. Energies 2019, 12, 2156.
- Kumar, K.P.; Saravanan, B. Recent Techniques to Model Uncertainties in Power Generation from Renewable Energy Sources and Loads in Microgrids—A Review. Renew. Sustain. Energy Rev. 2017, 71, 348–358.
- Hong, Y.-Y.; Apolinario, G.F.D. Uncertainty in Unit Commitment in Power Systems: A Review of Models, Methods, and Applications. Energies 2021, 14, 6658.
- Aien, M.; Hajebrahimi, A.; Fotuhi-Firuzabad, M. A Comprehensive Review on Uncertainty Modeling Techniques in Power System Studies. Renew. Sustain. Energy Rev. 2016, 57, 1077–1089.
- Soroudi, A.; Amraee, T. Decision Making under Uncertainty in Energy Systems: State of the Art. Renew. Sustain. Energy Rev. 2013, 28, 376–384.
- Meng, L.; Sanseverino, E.R.; Luna, A.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Microgrid Supervisory Controllers and Energy Management Systems: A Literature Review. Renew. Sustain. Energy Rev. 2016, 60, 1263–1273.
- Lefort, A.; Bourdais, R.; Ansanay-Alex, G.; Guéguen, H. Hierarchical Control Method Applied to Energy Management of a Residential House. Energy Build. 2013, 64, 53–61.
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; Vicuna, L.G.; de Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach Toward Standardization. IEEE Trans. Ind. Electron. 2010, 58, 158–172.
- Kaluthanthrige, R.; Rajapakse, A. Demand Response Integrated Day-Ahead Energy Management Strategy for Remote off-Grid Hybrid Renewable Energy Systems. Int. J. Electr. Power Energy Syst. 2021, 129, 106731.
- Haider, Z.M.; Mehmood, K.K.; Khan, S.U.; Khan, M.O.; Wadood, A.; Rhee, S.-B. Optimal Management of a Distribution Feeder During Contingency and Overload Conditions by Harnessing the Flexibility of Smart Loads. IEEE Access 2021, 9, 40124–40139.
- Jirdehi, M.A.; Tabar, V.S.; Ghassemzadeh, S.; Tohidi, S. Different Aspects of Microgrid Management: A Comprehensive Review. J. Energy Storage 2020, 30, 101457.
- Alavi, S.A.; Ahmadian, A.; Aliakbar-Golkar, M. Optimal Probabilistic Energy Management in a Typical Micro-Grid Based-on Robust Optimization and Point Estimate Method. Energy Convers. Manag. 2015, 95, 314–325.
- Xiao, F.; Ai, Q. New Modeling Framework Considering Economy, Uncertainty, and Security for Estimating the Dynamic Interchange Capability of Multi-Microgrids. Electr. Power Syst. Res. 2017, 152, 237–248.
- Soares, J.; Ghazvini, M.A.; Vale, Z.; Oliveira, P.B.d.M. A Multi-Objective Model for the Day-Ahead Energy Resource Scheduling of a Smart Grid with High Penetration of Sensitive Loads. Appl. Energy 2016, 162, 1074–1088.
- Kou, P.; Liang, D.; Gao, L. Stochastic Energy Scheduling in Microgrids Considering the Uncertainties in Both Supply and Demand. IEEE Syst. J. 2018, 12, 2589–2600.
- Karimi, H.; Jadid, S. Optimal Energy Management for Multi-Microgrid Considering Demand Response Programs: A Stochastic Multi-Objective Framework. Energy 2020, 195, 116992.
- Zhang, Y.; Gatsis, N.; Giannakis, G.B. Robust Energy Management for Microgrids With High-Penetration Renewables. IEEE Trans. Sustain. Energy 2013, 4, 944–953.
- Carli, R.; Cavone, G.; Pippia, T.; Schutter, B.D.; Dotoli, M. Robust Optimal Control for Demand Side Management of Multi-Carrier Microgrids. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1338–1351.
- Trigkas, D.; Gravanis, G.; Diamantaras, K.; Voutetakis, S.; Papadopoulou, S. Energy Management in Microgrids Using Model Predictive Control Empowered with Artificial Intelligence. Chem. Eng. Trans. 2022, 94, 961–966.
- Feng, C.; Cui, M.; Hodge, B.-M.; Zhang, J. A Data-Driven Multi-Model Methodology with Deep Feature Selection for Short-Term Wind Forecasting. Appl. Energy 2017, 190, 1245–1257.
