1. Applications and Consequences

1.1. Applicability

The most common example of Bloch's theorem is describing electrons in a crystal. However, a Bloch-wave description applies more generally to any wave-like phenomenon in a periodic medium. For example, a periodic dielectric structure in electromagnetism leads to photonic crystals, and a periodic acoustic medium leads to phononic crystals. It is generally treated in the various forms of the dynamical theory of diffraction.

1.2. Wave Vector

 

A Bloch wave (bottom) can be broken up into the product of a periodic function (top) and a plane-wave (center). The left side and right side represent the same Bloch wave broken up in two different ways, involving the wave vector k₁ (left) or k₂ (right). The difference (k₁−k₂) is a reciprocal lattice vector. In all plots, blue is real part and red is imaginary part. https://handwiki.org/wiki/index.php?curid=2054241

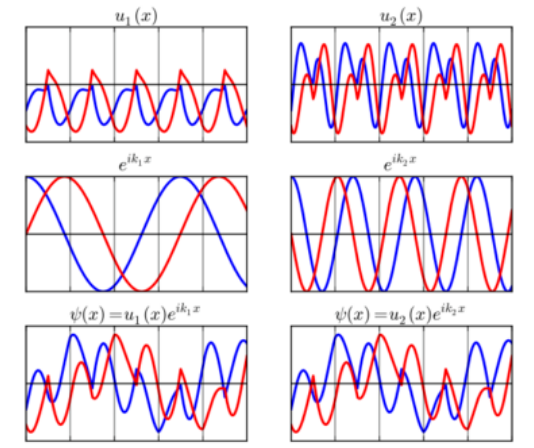
Suppose an electron is in a Bloch state

[math]\displaystyle{ \psi ( \mathbf{r} ) = \mathrm{e}^{ \mathrm{i} \mathbf{k} \cdot \mathbf{r} } u ( \mathbf{r} ) , }[/math]

where u is periodic with the same periodicity as the crystal lattice. The actual quantum state of the electron is entirely determined by [math]\displaystyle{ \psi }[/math], not k or u directly. This is important because k and u are not unique. Specifically, if [math]\displaystyle{ \psi }[/math] can be written as above using k, it can also be written using (k + K), where K is any reciprocal lattice vector (see figure at right). Therefore, wave vectors that differ by a reciprocal lattice vector are equivalent, in the sense that they characterize the same set of Bloch states.

The first Brillouin zone is a restricted set of values of k with the property that no two of them are equivalent, yet every possible k is equivalent to one (and only one) vector in the first Brillouin zone. Therefore, if we restrict k to the first Brillouin zone, then every Bloch state has a unique k. Therefore, the first Brillouin zone is often used to depict all of the Bloch states without redundancy, for example in a band structure, and it is used for the same reason in many calculations.

When k is multiplied by the reduced Planck's constant, it equals the electron's crystal momentum. Related to this, the group velocity of an electron can be calculated based on how the energy of a Bloch state varies with k; for more details see crystal momentum.

1.3. Detailed Example

For a detailed example in which the consequences of Bloch's theorem are worked out in a specific situation, see the article: Particle in a one-dimensional lattice (periodic potential).

2. Proof of Bloch's Theorem

Next, we prove Bloch's theorem:

For electrons in a perfect crystal, there is a basis of wavefunctions with the properties:

• Each of these wavefunctions is an energy eigenstate
• Each of these wavefunctions is a Bloch wave, meaning that this wavefunction [math]\displaystyle{ \psi }[/math] can be written in the form

[math]\displaystyle{ \psi(\mathbf{r}) = \mathrm{e}^{\mathrm{i}\mathbf{k}\cdot\mathbf{r}} u(\mathbf{r}) }[/math]

where u has the same periodicity as the atomic structure of the crystal.

2.1. Preliminaries: Crystal Symmetries, Lattice, and Reciprocal Lattice

The defining property of a crystal is translational symmetry, which means that if the crystal is shifted an appropriate amount, it winds up with all its atoms in the same places. (A finite-size crystal cannot have perfect translational symmetry, but it is a useful approximation.)

A three-dimensional crystal has three primitive lattice vectors a₁, a₂, a₃. If the crystal is shifted by any of these three vectors, or a combination of them of the form

[math]\displaystyle{ n_1 \mathbf{a}_1 + n_2 \mathbf{a}_2 + n_3 \mathbf{a}_3 }[/math]

where n_i are three integers, then the atoms end up in the same set of locations as they started.

Another helpful ingredient in the proof is the reciprocal lattice vectors. These are three vectors b₁, b₂, b₃ (with units of inverse length), with the property that a_i · b_i = 2π, but a_i · b_j = 0 when i ≠ j. (For the formula for b_i, see reciprocal lattice vector.)

2.2. Lemma about Translation Operators

Let [math]\displaystyle{ \hat{T}_{n_1,n_2,n_3} \! }[/math] denote a translation operator that shifts every wave function by the amount n₁a₁ + n₂a₂ + n₃a₃ (as above, n_j are integers). The following fact is helpful for the proof of Bloch's theorem:

Lemma: If a wavefunction [math]\displaystyle{ \psi }[/math] is an eigenstate of all of the translation operators (simultaneously), then [math]\displaystyle{ \psi }[/math] is a Bloch wave.

Proof: Assume that we have a wavefunction [math]\displaystyle{ \psi }[/math] which is an eigenstate of all the translation operators. As a special case of this,

[math]\displaystyle{ \psi(\mathbf{r}+\mathbf{a}_j) = C_j \psi(\mathbf{r}) }[/math]

for j = 1, 2, 3, where C_j are three numbers (the eigenvalues) which do not depend on r. It is helpful to write the numbers C_j in a different form, by choosing three numbers θ₁, θ₂, θ₃ with e^2πiθ_j = C_j:

[math]\displaystyle{ \psi(\mathbf{r}+\mathbf{a}_j) = \mathrm{e}^{2 \pi \mathrm{i} \theta_j} \psi(\mathbf{r}) }[/math]

Again, the θ_j are three numbers which do not depend on r. Define k = θ₁b₁ + θ₂b₂ + θ₃b₃, where b_j are the reciprocal lattice vectors (see above). Finally, define

[math]\displaystyle{ u(\mathbf{r}) = \mathrm{e}^{-\mathrm{i} \mathbf{k}\cdot\mathbf{r}} \psi(\mathbf{r})\,. }[/math]

Then

[math]\displaystyle{ u(\mathbf{r} + \mathbf{a}_j) = \mathrm{e}^{-\mathrm{i}\mathbf{k} \cdot (\mathbf{r} + \mathbf{a}_j)} \psi(\mathbf{r}+\mathbf{a}_j) = \big( \mathrm{e}^{-\mathrm{i}\mathbf{k} \cdot \mathbf{r}} \mathrm{e}^{-\mathrm{i}\mathbf{k}\cdot \mathbf{a}_j} \big) \big( \mathrm{e}^{2\pi \mathrm{i} \theta_j} \psi(\mathbf{r}) \big) = \mathrm{e}^{-\mathrm{i}\mathbf{k} \cdot \mathbf{r}} \mathrm{e}^{-2\pi \mathrm{i} \theta_j} \mathrm{e}^{2\pi \mathrm{i} \theta_j} \psi(\mathbf{r}) = u(\mathbf{r}) }[/math].

This proves that u has the periodicity of the lattice. Since [math]\displaystyle{ \psi(\mathbf{r}) = \mathrm{e}^{\mathrm{i} \mathbf{k}\cdot\mathbf{r}} u(\mathbf{r}) }[/math], that proves that the state is a Bloch wave.

2.3. Proof

Finally, we are ready for the main proof of Bloch's theorem which is as follows.

As above, let [math]\displaystyle{ \hat{T}_{n_1,n_2,n_3} \! }[/math] denote a translation operator that shifts every wave function by the amount n₁a₁ + n₂a₂ + n₃a₃, where n_i are integers. Because the crystal has translational symmetry, this operator commutes with the Hamiltonian operator. Moreover, every such translation operator commutes with every other. Therefore, there is a simultaneous eigenbasis of the Hamiltonian operator and every possible [math]\displaystyle{ \hat{T}_{n_1,n_2,n_3} \! }[/math] operator. This basis is what we are looking for. The wavefunctions in this basis are energy eigenstates (because they are eigenstates of the Hamiltonian), and they are also Bloch waves (because they are eigenstates of the translation operators; see Lemma above).

3. History and Related Equations

The concept of the Bloch state was developed by Felix Bloch in 1928,^[1] to describe the conduction of electrons in crystalline solids. The same underlying mathematics, however, was also discovered independently several times: by George William Hill (1877),^[2] Gaston Floquet (1883),^[3] and Alexander Lyapunov (1892).^[4] As a result, a variety of nomenclatures are common: applied to ordinary differential equations, it is called Floquet theory (or occasionally the Lyapunov–Floquet theorem). The general form of a one-dimensional periodic potential equation is Hill's equation:^[5]

[math]\displaystyle{ \frac {d^2y}{dt^2}+f(t) y=0, }[/math]

where f(t) is a periodic potential. Specific periodic one-dimensional equations include the Kronig–Penney model and Mathieu's equation.

Mathematically Bloch's theorem is interpreted in terms of unitary characters of a lattice group, and is applied to spectral geometry.^[6][7][8]