1. Random Mouse Algorithm

This is a trivial method that can be implemented by a very unintelligent robot or perhaps a mouse. It is simply to proceed following the current passage until a junction is reached, and then to make a random decision about the next direction to follow. Although such a method would always eventually find the right solution, this algorithm can be extremely slow.

2. Wall Follower

Traversal using right-hand rule. https://handwiki.org/wiki/index.php?curid=1987617

Maze with two solutions. https://handwiki.org/wiki/index.php?curid=1633670

Solution to above maze. The solution is the boundary between the connected components of the wall of the maze, each represented by a different color. https://handwiki.org/wiki/index.php?curid=1584916

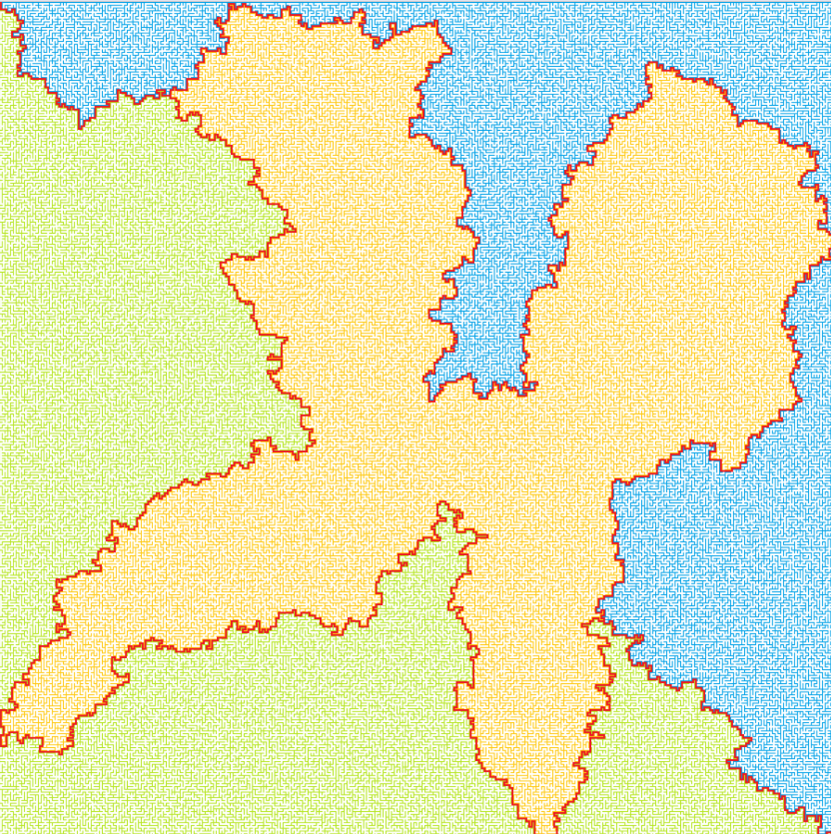
The best-known rule for traversing mazes is the wall follower, also known as either the left-hand rule or the right-hand rule. If the maze is simply connected, that is, all its walls are connected together or to the maze's outer boundary, then by keeping one hand in contact with one wall of the maze the solver is guaranteed not to get lost and will reach a different exit if there is one; otherwise, the algorithm will return to the entrance having traversed every corridor next to that connected section of walls at least once.

Another perspective into why wall following works is topological. If the walls are connected, then they may be deformed into a loop or circle.^[1] Then wall following reduces to walking around a circle from start to finish. To further this idea, notice that by grouping together connected components of the maze walls, the boundaries between these are precisely the solutions, even if there is more than one solution (see figures on the right).

If the maze is not simply-connected (i.e. if the start or endpoints are in the center of the structure surrounded by passage loops, or the pathways cross over and under each other and such parts of the solution path are surrounded by passage loops), this method will not reach the goal.

Another concern is that care should be taken to begin wall-following at the entrance to the maze. If the maze is not simply-connected and one begins wall-following at an arbitrary point inside the maze, one could find themselves trapped along a separate wall that loops around on itself and containing no entrances or exits. Should it be the case that wall-following begins late, attempt to mark the position in which wall-following began. Because wall-following will always lead you back to where you started, if you come across your starting point a second time, you can conclude the maze is not simply-connected, and you should switch to an alternative wall not yet followed. See the Pledge Algorithm, below, for an alternative methodology.

Wall-following can be done in 3D or higher-dimensional mazes if its higher-dimensional passages can be projected onto the 2D plane in a deterministic manner. For example, if in a 3D maze "up" passages can be assumed to lead Northwest, and "down" passages can be assumed to lead southeast, then standard wall following rules can apply. However, unlike in 2D, this requires that the current orientation is known, to determine which direction is the first on the left or right.

3. Pledge Algorithm

Left: Left-turn solver trapped

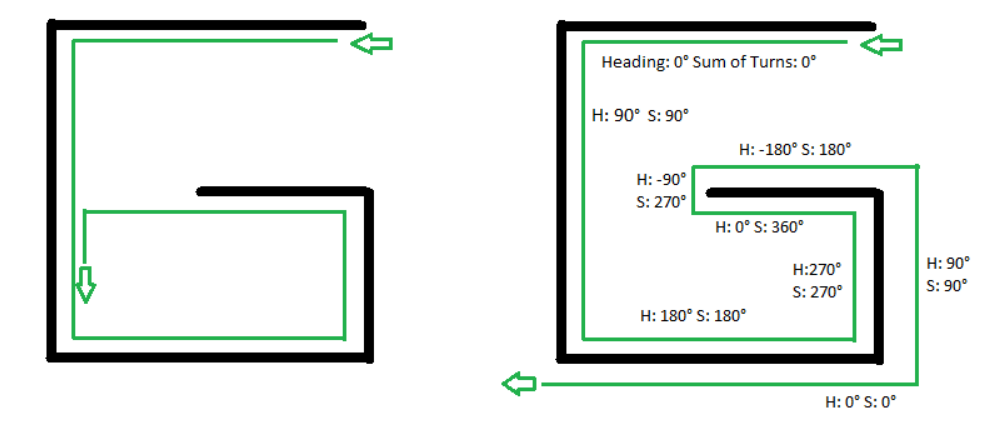
Right: Pledge algorithm solution

Disjoint mazes can be solved with the wall follower method, so long as the entrance and exit to the maze are on the outer walls of the maze. If however, the solver starts inside the maze, it might be on a section disjoint from the exit, and wall followers will continually go around their ring. The Pledge algorithm (named after Jon Pledge of Exeter) can solve this problem.^[2][3]

The Pledge algorithm, designed to circumvent obstacles, requires an arbitrarily chosen direction to go toward, which will be preferential. When an obstacle is met, one hand (say the right hand) is kept along the obstacle while the angles turned are counted (clockwise turn is positive, counter-clockwise turn is negative). When the solver is facing the original preferential direction again, and the angular sum of the turns made is 0, the solver leaves the obstacle and continues moving in its original direction.

The hand is removed from the wall only when both "sum of turns made" and "current heading" are at zero. This allows the algorithm to avoid traps shaped like an upper case letter "G". Assuming the algorithm turns left at the first wall, one gets turned around a full 360 degrees by the walls. An algorithm that only keeps track of "current heading" leads into an infinite loop as it leaves the lower rightmost wall heading left and runs into the curved section on the left hand side again. The Pledge algorithm does not leave the rightmost wall due to the "sum of turns made" not being zero at that point (note 360 degrees is not equal to 0 degrees). It follows the wall all the way around, finally leaving it heading left outside and just underneath the letter shape.

This algorithm allows a person with a compass to find their way from any point inside to an outer exit of any finite two-dimensional maze, regardless of the initial position of the solver. However, this algorithm will not work in doing the reverse, namely finding the way from an entrance on the outside of a maze to some end goal within it.

4. Trémaux's Algorithm

https://handwiki.org/wiki/index.php?curid=1359400

Trémaux's algorithm. The large green dot shows the current position, the small blue dots show single marks on paths, and the red crosses show double marks. Once the exit is found, the route is traced through the singly-marked paths.

Trémaux's algorithm, invented by Charles Pierre Trémaux,^[4] is an efficient method to find the way out of a maze that requires drawing lines on the floor to mark a path, and is guaranteed to work for all mazes that have well-defined passages,^[5] but it is not guaranteed to find the shortest route.

A path from a junction is either unvisited, marked once or marked twice. The algorithm works according to the following rules:

• Mark each path once, when you follow it. The marks need to be visible at both ends of the path. Therefore, if they are being made as physical marks, rather than stored as part of a computer algorithm, the same mark should be made at both ends of the path.
• Never enter a path which has two marks on it.
• If you arrive at a junction that has no marks (except possibly for the one on the path by which you entered), choose an arbitrary unmarked path, follow it, and mark it.
• Otherwise:
  • If the path you came in on has only one mark, turn around and return along that path, marking it again. In particular this case should occur whenever you reach a dead end.
  • If not, choose arbitrarily one of the remaining paths with the fewest marks (zero if possible, else one), follow that path, and mark it.

The "turn around and return" rule effectively transforms any maze with loops into a simply connected one; whenever we find a path that would close a loop, we treat it as a dead end and return. Without this rule, it is possible to cut off one's access to still-unexplored parts of a maze if, instead of turning back, we arbitrarily follow another path.

When you finally reach the solution, paths marked exactly once will indicate a way back to the start. If there is no exit, this method will take you back to the start where all paths are marked twice. In this case each path is walked down exactly twice, once in each direction. The resulting walk is called a bidirectional double-tracing.^[6]

Essentially, this algorithm, which was discovered in the 19th century, has been used about a hundred years later as depth-first search.^[7][8]

5. Dead-end Filling

Dead-end filling is an algorithm for solving mazes that fills all dead ends, leaving only the correct ways unfilled. It can be used for solving mazes on paper or with a computer program, but it is not useful to a person inside an unknown maze since this method looks at the entire maze at once. The method is to 1) find all of the dead-ends in the maze, and then 2) "fill in" the path from each dead-end until the first junction is met. Note that some passages won't become parts of dead end passages until other dead ends are removed first. A video of dead-end filling in action can be seen here: [1][2].

Dead-end filling cannot accidentally "cut off" the start from the finish since each step of the process preserves the topology of the maze. Furthermore, the process won't stop "too soon" since the end result cannot contain any dead-ends. Thus if dead-end filling is done on a perfect maze (maze with no loops), then only the solution will remain. If it is done on a partially braid maze (maze with some loops), then every possible solution will remain but nothing more. [3]

6. Recursive Algorithm

If given an omniscient view of the maze, a simple recursive algorithm can tell one how to get to the end. The algorithm will be given a starting X and Y value. If the X and Y values are not on a wall, the method will call itself with all adjacent X and Y values, making sure that it did not already use those X and Y values before. If the X and Y values are those of the end location, it will save all the previous instances of the method as the correct path. Here is a sample code in Java:

int[][] maze = new int[width][height]; // The maze boolean[][] wasHere = new boolean[width][height]; boolean[][] correctPath = new boolean[width][height]; // The solution to the maze int startX, startY; // Starting X and Y values of maze int endX, endY; // Ending X and Y values of maze public void solveMaze() { maze = generateMaze(); // Create Maze (1 = path, 2 = wall) for (int row = 0; row < maze.length; row++) // Sets boolean Arrays to default values for (int col = 0; col < maze[row].length; col++){ wasHere[row][col] = false; correctPath[row][col] = false; } boolean b = recursiveSolve(startX, startY); // Will leave you with a boolean array (correctPath) // with the path indicated by true values. // If b is false, there is no solution to the maze } public boolean recursiveSolve(int x, int y) { if (x == endX && y == endY) return true; // If you reached the end if (maze[x][y] == 2 || wasHere[x][y]) return false; // If you are on a wall or already were here wasHere[x][y] = true; if (x != 0) // Checks if not on left edge if (recursiveSolve(x-1, y)) { // Recalls method one to the left correctPath[x][y] = true; // Sets that path value to true; return true; } if (x != width - 1) // Checks if not on right edge if (recursiveSolve(x+1, y)) { // Recalls method one to the right correctPath[x][y] = true; return true; } if (y != 0) // Checks if not on top edge if (recursiveSolve(x, y-1)) { // Recalls method one up correctPath[x][y] = true; return true; } if (y != height - 1) // Checks if not on bottom edge if (recursiveSolve(x, y+1)) { // Recalls method one down correctPath[x][y] = true; return true; } return false; }

7. Maze-routing Algorithm

The maze-routing algorithm ^[9] is a low overhead method to find the way between any two locations of the maze. The algorithm is initially proposed for chip multiprocessors (CMPs) domain and guarantees to work for any grid-based maze. In addition to finding paths between two location of the grid (maze), the algorithm can detect when there is no path between the source and destination. Also, the algorithm is to be used by an inside traveler with no prior knowledge of the maze with fixed memory complexity regardless of the maze size; requiring 4 variables in total for finding the path and detecting the unreachable locations. Nevertheless, the algorithm is not to find the shortest path.

Maze-routing algorithm uses the notion of Manhattan distance (MD) and relies on the property of grids that the MD increments/decrements exactly by 1 when moving from one location to any 4 neighboring locations. Here is the pseudocode without the capability to detect unreachable locations.

Point src, dst;// Source and destination coordinates // cur also indicates the coordinates of the current location int MD_best = MD(src, dst);// It stores the closest MD we ever had to dst // A productive path is the one that makes our MD to dst smaller while (cur != dst) { if (there exists a productive path) { Take the productive path; } else { MD_best = MD(cur, dst); Imagine a line between cur and dst; Take the first path in the left/right of the line; // The left/right selection affects the following hand rule while (MD(cur, dst) != MD_best || there does not exist a productive path) { Follow the right-hand/left-hand rule; // The opposite of the selected side of the line } }

8. Shortest Path Algorithm

A maze with many solutions and no dead-ends, where it may be useful to find the shortest path. https://handwiki.org/wiki/index.php?curid=1730199

When a maze has multiple solutions, the solver may want to find the shortest path from start to finish. There are several algorithms to find shortest paths, most of them coming from graph theory. One such algorithm finds the shortest path by implementing a breadth-first search, while another, the A* algorithm, uses a heuristic technique. The breadth-first search algorithm uses a queue to visit cells in increasing distance order from the start until the finish is reached. Each visited cell needs to keep track of its distance from the start or which adjacent cell nearer to the start caused it to be added to the queue. When the finish location is found, follow the path of cells backwards to the start, which is the shortest path. The breadth-first search in its simplest form has its limitations, like finding the shortest path in weighted graphs.