A new type of electrolysis, initially known as the contact glow-discharge electrolysis (CGDE) and, more recently, as the plasma-driven solution electrolysis (PDSE), has attracted attention as an alternative method of hydrogen production. PDSE is a nontypical electrochemical process in which electric plasma is formed in the glow discharges excited by the direct or pulsed current in a gas–vapor envelope in the vicinity of the discharge electrode immersed in the electrolytic solution. The yield of chemicals in PDSE (i.e., the ratio of the moles of the product formed to the moles of electrons consumed in a chemical reaction) is several times higher than the Faradaic production of chemicals (predicted by Faraday’s law). In PDSE, new chemical compounds can also be synthesized, which does not happen using Faradaic electrolysis.
- electrolytic solution
- plasma electrolysis
- contact glow-discharge electrolysis (CGDE)
- plasma-driven solution electrolysis (PDSE)
- hydrogen
- hydrogen production
1. Introduction
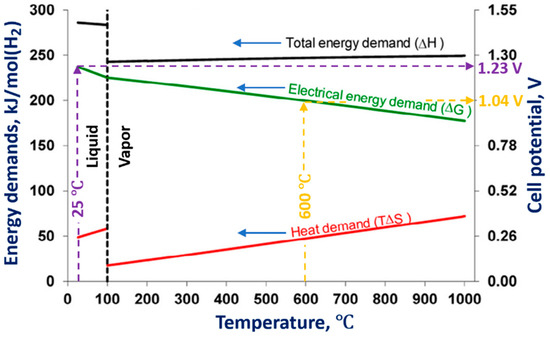
2. Faradaic Electrolysis
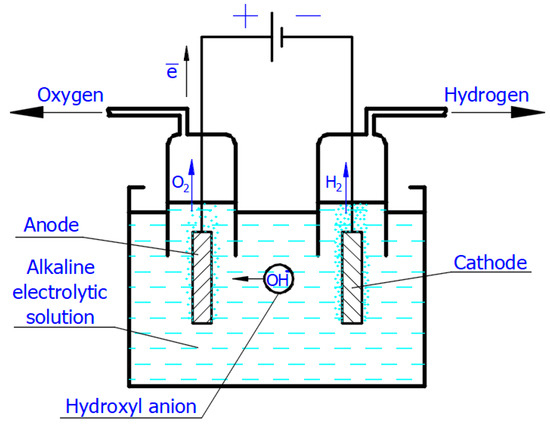
It is well known that electrolysis is an electrochemical process that occurs when a direct or pulsed current passes through the electrolytic cell. To perform electrolysis, the electrolytic cell must contain the following essential components:-
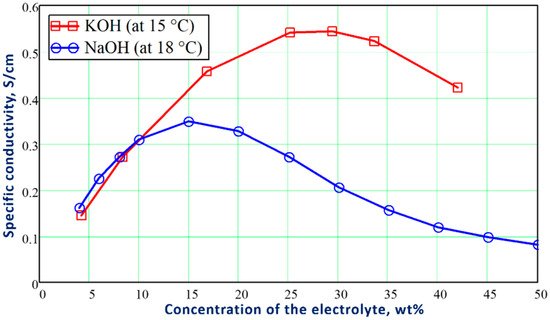
An electrolytic solution containing free ions, which can carry an electric current. In the Faradaic electrolysis of acidic and alkaline aqueous solutions, strong acids and alkalis, such as sulfuric acid (H2SO4), potassium (KOH), and sodium (NaOH) hydroxides, are used as electrolytes due to their strong ability to dissociate into positive ions (called cations) and negatively charged ions (called anions), which easily conduct electricity in the electrolytic solution [6][7][8].
-
A direct or pulsed current supply, which provides the necessary energy to create the direct motion of ions in the electrolytic solution.
-
Additionally, two electrodes, which are electrical conductors providing physical contact between the current supply and the electrolytic solution. In alkaline electrolysis, low-cost, non-precious, nickel-based alloys and stainless steel are used as the cathode and anode electrode materials, respectively [9][10].
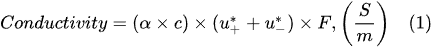
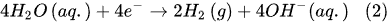

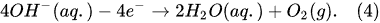
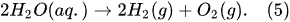
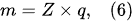
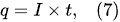
3. Transformation of the Faradaic Electrolysis into PDSE
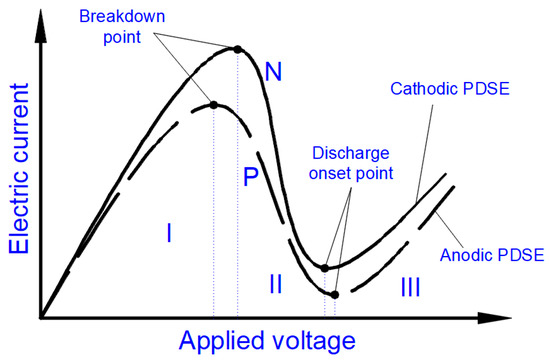
The Faradaic electrolysis transforms into PDSE with an increased applied voltage that has a value sufficient to ionize the species in the gas–vapor envelope at the electrode, and subsequently, induce the electrical discharge plasma in the envelope. Regardless of the electric potential polarity, the plasma is formed at the electrode, which its active surface area (immersed in the electrolytic solution) is smaller than that of the other electrode. The electrode at which the plasma is formed is called the discharge electrode [20]. If the smaller electrode is positively charged (being an anode), the discharge formed around it is called the anodic glow discharge. If the smaller electrode is negatively charged (being a cathode), the discharge around it is called the cathodic glow discharge (see Figure 4). Correspondingly, PDSE is either the anodic or cathodic regime of PDSE. The length of electrodes exposed to the electrolytic solution is called the active length of the electrodes. In the anodic and cathodic regimes of PDSE, the plasma around the discharge electrode takes over the role of the positive and negative electrode, respectively, whereas the second electrode (larger one) immersed in the electrolytic solution with no plasma formation acts as a counter electrode. In PDSE, the plasma–liquid interaction allows both electrochemical and plasma-chemical synthesis of the substances [1][21]. Figure 4a–e illustrates the transformation of the electrolysis from its Faradaic form into PDSE. Figure 4a shows a typical electrolytic cell with a smaller and a larger electrode for PDSE before applying DC voltage. Figure 4b,d illustrates the formation of PDSE at the anode with the applied voltage, whereas Figure 4c,e illustrates the formation of PDSE at the cathode. Figure 4b–e confirms that, regardless of the voltage polarity, both glow discharges, the anodic and cathodic, form at the electrode of a smaller active surface area, i.e., at the tungsten rod whose surface area is about 12 times smaller than that of the stainless-steel plate. In the anodic regime of PDSE, the plasma forms a thin layer around the tungsten rod (Figure 4d). The plasma formed in the cathodic regime of PDSE (Figure 4e) occupies a much larger volume around the tungsten rod than that in the anodic regime of PDSE (Figure 4d). This shows that the cathodic regime of PDSE is more efficient for steam generation. The brightness of the cathodic glow discharges is stronger than that of the anodic glow discharges, although the applied voltage is lower in the cathodic regime of PDSE (120 V in the cathodic regime of PDSE versus 130 V in the anodic regime of PDSE). Sharma et al. [22] confirmed that the cathodic regime of PDSE can be applied for continuous steam generation with a steam generation efficiency of 80%. Zheng et al. [23] showed that in the cathodic regime of PDSE, the plasma formed around the discharge electrode is highly negative. The above differences in the microscopic appearance of the anodic and cathodic regimes of PDSE are due to the difference in the mechanisms of the formation of the glow discharges at the anode and cathode.
4. Physicochemical Processes Occurring in the Cathodic and Anodic Regimes of PDSE
Previous studies [1][2][3][4][5][33] showed that in PDSE, the total yields (total amount of all substances produced at the discharge electrode) include chemical yields produced according to Faraday’s first law of electrolysis (Equation (6)), called the Faradaic yield (products), and extra amount of substances, the production of which does not obey Equation (6). This extra amount of substances is called the non-Faradaic yield (products). The non-Faradaic yield of the anodic and cathodic regimes of PDSE is derived from two different reaction regions (Figure 6): i.e., the plasma region around the discharge electrode and the interfacial region (the aqueous electrolytic solution situated close to the plasma interface).

4.1. Water-Vapor Decomposition in the Plasma Region
In the plasma around the discharge electrode, one of the mechanisms of the decomposition of water-vapor molecules into H2 and O2 molecules is a mechanism observed for the water-vapor decomposition in electrical discharges [40]. Mededovic and Locke [41] developed a model of plasma-in-liquid discharges. In this model, the plasma region consists of two subregions: inner and outer. Following up with the model developed by Mededovic and Locke [41], we may also assume the same subregions surrounding the discharge electrode in PDSE (Figure 6): an inner subregion, situated close to the discharge electrode with ionizing plasma, which dissociates water into OH* and H* radicals by the electron-impact and thermal processes, and an outer subregion, situated close to the plasma interface, in which radicals recombine, producing long-lived molecules such as H2, O2, and H2O2. The modeling results were confirmed experimentally in [41]. The set of the corresponding reactions occurring in those two subregions is presented below. The water-vapor decomposition in the inner plasma subregion follows the reactions [41][42]: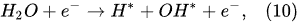
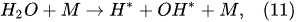
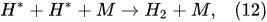
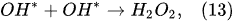
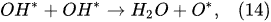
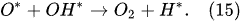
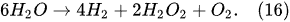
Plasma–Liquid Interaction in the Cathodic Regime of PDSE
In the interfacial region (Figure 6), in the liquid-phase reaction zone near the plasma interface, one of the mechanisms responsible for the breakup of liquid H2O molecules into H2, H2O2, and O2 is the radiolysis-based reactions. As shown by Mota-Lima et al. [43], in the cathodic regime of PDSE, the ballistic electrons are released from the plasma region into the liquid interfacial region at a rate which can be estimated by the following equation [43]: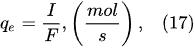
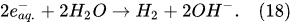

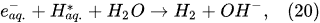
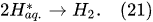
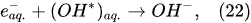
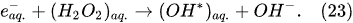
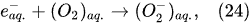
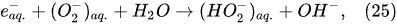

Plasma–Liquid Interaction in the Anodic Regime of PDSE
In the anodic regime of PDSE, one of the mechanisms of the plasma–liquid interaction follows Hickling’s radiolytic mechanism [26]. According to this mechanism, each H2O+gas ion, after acceleration in the steep anode, falls near the interfacial region and is driven into the aqueous electrolytic solution with energies sufficient to break-up liquid water molecules into H* and OH* radicals. Then, the formed radicals diffuse into the bulk of the electrolytic solution, where they undergo several reactions which are known to occur in pulse radiolysis. The relative importance of the two mechanisms occurring in the plasma region (i.e., bombardment of the interfacial region by H2O+gas ions) and the interfacial region (i.e., diffusion of H2O+gas ions into the interfacial region with the subsequent break-up of the liquid water molecules) depends on the magnitude of the applied voltage. At the discharge onset voltage of 420 V, the occurring mechanism is the liquid-phase Hickling’s radiolytic mechanism, accounting for 90% of the non-Faradaic yield. However, with a further rise in voltage, the gas-phase mechanism, described in [5], becomes increasingly important and, at 500 V, accounts for 75% of the non-Faradaic yield. For more details on the charge-transfer mechanisms in the anodic regime of PDSE, refer to the recent comprehensive study from Yerokhin et al. [45]. The Faradaic efficiency of hydrogen production in the plasma-driven solution electrolysis (PDSE), which exceeds 100%, is explained by different, in terms of their nature, reactions occurring in the vicinity of the discharge electrode. The first reaction type is based on the charge transfer. According to Faraday’s first law of electrolysis, hydrogen generation is directly proportional to the electric current passed through the electrolytic solution. In contrast to conventional electrolysis, a second mechanism consists of the gas-phase reactions in the plasma region. A solvent (water) and the organic additives, if any, are evaporated by the intense heating effect of the discharge plasma into the plasma region, where they serve as an additional source of hydrogen. The electron-impact decomposition of molecules in the plasma region is not based on the charge transfer and is non-Faradaic. The two reaction mechanisms, one in the liquid interfacial region and another in the plasma region, produce hydrogen simultaneously. Therefore, the electron-impact decomposition occurring in the plasma region contributes to the Faradaic efficiency of more than 100%. Moreover, three additional processes are also responsible for decomposing the water molecules and molecules of organic additives, if any, in the interfacial and plasma regions. They are photodecomposition, ion-impact decomposition, and thermal decomposition. These reaction pathways are not based on the charge transfer and they are non-Faradaic as well. The actual reactions occurring within the plasma and interfacial regions in the anodic and cathodic regimes of PDSE are much more sophisticated than those shown above. Potential mechanisms of these interactions will be discussed in aour future research paper dedicated to the fundamentals of PDSE.References
- Susanta K Sen Gupta; Rajshree Singh; Cathodic contact glow discharge electrolysis: its origin and non-faradaic chemical effects. Plasma Sources Science and Technology 2016, 26, 015005, 10.1088/0963-0252/26/1/015005.
- Susanta K. Sengupta; Om Prakash Singh; Contact glow discharge electrolysis: a study of its chemical yields in aqueous inert-type electrolytes. Journal of Electroanalytical Chemistry 1994, 369, 113-120, 10.1016/0022-0728(94)87089-6.
- Susanta K. Sengupta; Ashok K. Srivastava; Rajeshwar Singh; Contact glow discharge electrolysis: a study on its origin in the light of the theory of hydrodynamic instabilities in local solvent vaporisation by Joule heating during electrolysis. Journal of Electroanalytical Chemistry 1997, 427, 23-27, 10.1016/s0022-0728(96)05044-9.
- Susanta K. Sengupta; Rajeshwar Singh; Ashok K. Srivastava; A Study on the Origin of Nonfaradaic Behavior of Anodic Contact Glow Discharge Electrolysis: The Relationship Between Power Dissipated in Glow Discharges and Nonfaradaic Yields. Journal of The Electrochemical Society 1998, 145, 2209-2213, 10.1149/1.1838621.
- Urvashi Gangal; Monika Srivastava; Susanta K. Sen Gupta; Mechanism of the Breakdown of Normal Electrolysis and the Transition to Contact Glow Discharge Electrolysis. Journal of The Electrochemical Society 2009, 156, F131, 10.1149/1.3186023.
- Maximilian Schalenbach; Geert Tjarks; Marcelo Carmo; Wiebke Lueke; Martin Mueller; Detlef Stolten; Acidic or Alkaline? Towards a New Perspective on the Efficiency of Water Electrolysis. Journal of The Electrochemical Society 2016, 163, F3197-F3208, 10.1149/2.0271611jes.
- Marcelo Carmo; David L. Fritz; Jürgen Mergel; Detlef Stolten; A comprehensive review on PEM water electrolysis. International Journal of Hydrogen Energy 2013, 38, 4901-4934, 10.1016/j.ijhydene.2013.01.151.
- Qing Lei; Baoguo Wang; Peican Wang; Shuai Liu; Hydrogen generation with acid/alkaline amphoteric water electrolysis. Journal of Energy Chemistry 2019, 38, 162-169, 10.1016/j.jechem.2018.12.022.
- Alejandro N. Colli; Hubert H. Girault; Alberto Battistel; Non-Precious Electrodes for Practical Alkaline Water Electrolysis. Materials 2019, 12, 1336, 10.3390/ma12081336.
- Keith Scott. Chapter 1 Introduction to Electrolysis, Electrolysers and Hydrogen Production. In Electrochemical Methods for Hydrogen Production; Keith Scott, Eds.; Royal Society of Chemistry: London, UK, 2019; pp. 1-27.
- Zinchenko A.V., Izotova S.G., Rumyantsev A.V., Simanova S.A., Skripkin M.U., Slobodov A.A.. New Handbook of Chemist and Process Engineer. Chemical Equilibrium. Properties of Solutions (in Russian); Simanova S.A., Eds.; Professional: Saint Petersburg, Russia, 2004; pp. 998.
- Atkins, P.; de Paula, J.. Atkin’s Physical Chemistry; Jonathan Crowe, Jessica Fiorillo, Ruth Hughes, Eds.; W.H. Freeman and Company: New York, NY, USA, 2006; pp. 1085.
- Coutanceau, C.; Baranton, S.; Audichon, T.. Chapter 3-Hydrogen Production From Water Electrolysis. Hydrogen Electrochemical Production.; Christophe Coutanceau, Stève Baranton, Thomas Audichon, Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 17-62.
- Mariana C. O. Monteiro; Akansha Goyal; Pricilla Moerland; Marc T. M. Koper; Understanding Cation Trends for Hydrogen Evolution on Platinum and Gold Electrodes in Alkaline Media. ACS Catalysis 2021, 11, 14328-14335, 10.1021/acscatal.1c04268.
- Ali Keçebaş, Muhammet Kayfeci, Mutlucan Bayat. Chapter 9-Electrochemical hydrogen generation. In Solar Hydrogen Production; Francesco Calise, Massimo Dentice D’Accadia, Massimo Santarelli, Andrea Lanzini, Domenico Ferrero, Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 299–317.
- Elektrochemisches Äquivalent . Wikipedia. Retrieved 2022-10-28
- Sanford Klein, Gregory Nellis. Thermodynamics; Cambridge University Press: Cambridge, MA, USA, 2012; pp. 1102.
- Alexander Buttler; Hartmut Spliethoff; Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: A review. Renewable and Sustainable Energy Reviews 2018, 82, 2440-2454, 10.1016/j.rser.2017.09.003.
- Sukhvinder P.S. Badwal; Sarbjit Giddey; Christopher Munnings; Hydrogen production via solid electrolytic routes. WIREs Energy and Environment 2012, 2, 473-487, 10.1002/wene.50.
- ZongCheng Yan; Li Chen; Honglin Wang; Hydrogen generation by glow discharge plasma electrolysis of ethanol solutions. Journal of Physics D: Applied Physics 2008, 41, 155205, 10.1088/0022-3727/41/15/155205.
- Peter J. Bruggeman; Renee R. Frontiera; Uwe R. Kortshagen; Mark J. Kushner; Suljo Linic; George C. Schatz; Himashi Andaraarachchi; Stephen Exarhos; Leighton O. Jones; Chelsea M. Mueller; et al.Christopher C. RichChi XuYuanfu YueYi Zhang Plasma-driven solution electrolysis. Journal of Applied Physics 2021, 129, 200902, 10.1063/5.0044261.
- Neeraj Sharma; Gerardo Diaz; Edbertho Leal-Quirós; Evaluation of contact glow-discharge electrolysis as a viable method for steam generation. Electrochimica Acta 2013, 108, 330-336, 10.1016/j.electacta.2013.06.108.
- Bocong Zheng; Keliang Wang; Maheshwar Shrestha; Thomas Schuelke; Qi Hua Fan; Understanding the chemical reactions in cathodic plasma electrolysis. Plasma Sources Science and Technology 2019, 28, 085016, 10.1088/1361-6595/ab36a6.
- Sergii Bespalko; The plasma discharges in the anodic and cathodic regimes of plasma driven solution electrolysis for hydrogen production. PRZEGLĄD ELEKTROTECHNICZNY 2022, 1, 124-127, 10.15199/48.2022.09.26.
- Anis Allagui; Ahmed S. Elwakil; On the N-shaped Conductance and Hysteresis Behavior of Contact Glow Discharge Electrolysis. Electrochimica Acta 2015, 168, 173-177, 10.1016/j.electacta.2015.03.154.
- A. Hickling; M. D. Ingram; Contact glow-discharge electrolysis. Trans. Faraday Soc. 1964, 60, 783-793, 10.1039/tf9646000783.
- Zong Cheng Yan; Chen Li; Wang Hong Lin; Hydrogen generation by glow discharge plasma electrolysis of methanol solutions. International Journal of Hydrogen Energy 2009, 34, 48-55, 10.1016/j.ijhydene.2008.09.099.
- Gao Jinzhang; Wang Aixiang; Fu Yan; Wu Jianlin; Ma Dongping; Guo Xiao; Li Yan; Yang Wu; Analysis of Energetic Species Caused by Contact Glow Discharge Electrolysis in Aqueous Solution. Plasma Science and Technology 2008, 10, 30-38, 10.1088/1009-0630/10/1/07.
- Genki Saito; Yuki Nakasugi; Tomohiro Akiyama; Generation of solution plasma over a large electrode surface area. Journal of Applied Physics 2015, 118, 023303, 10.1063/1.4926493.
- Xing-Long Jin; Xiao-Yan Wang; Hong-Mei Zhang; Qing Xia; Dong-Bin Wei; Jun-Jie Yue; Influence of Solution Conductivity on Contact Glow Discharge Electrolysis. Plasma Chemistry and Plasma Processing 2010, 30, 429-436, 10.1007/s11090-010-9220-0.
- Xinglong Jin; Xiaoyan Wang; Junjie Yue; Yaqi Cai; Hongyu Zhang; The effect of electrolyte constituents on contact glow discharge electrolysis. Electrochimica Acta 2010, 56, 925-928, 10.1016/j.electacta.2010.09.079.
- Giovanni Battista Alteri; Matteo Bonomo; Franco Decker; Danilo Dini; Contact Glow Discharge Electrolysis: Effect of Electrolyte Conductivity on Discharge Voltage. Catalysts 2020, 10, 1104, 10.3390/catal10101104.
- Gao Jin-Zhang; Wang Xiao-Yan; Hu Zhong-Ai; Hou Jing-Guo; Lu Quan-Fang; A Review on Chemical Effects in Aqueous Solution induced by Plasma with Glow Discharge. Plasma Science and Technology 2001, 3, 765-774, 10.1088/1009-0630/3/3/003.
- Jen-Shih Chang, Arnold J. Kelly, Joseph M. Crowley. Handbook of Electrostatic Processes; Marcel Dekker Inc.: New York, NY, USA, 1995; pp. 763.
- T. Paulmier; J.M. Bell; P.M. Fredericks; Development of a novel cathodic plasma/electrolytic deposition technique: Part 2: Physico-chemical analysis of the plasma discharge. Surface and Coatings Technology 2007, 201, 8771-8781, 10.1016/j.surfcoat.2006.07.066.
- Gamburg, D.Y.; Semenov, V.P.; Dubovkin, N.F.. Hydrogen: Properties, Production, Storage, Transportation, and Applications (in Russian); Khimiya: Moscow, Russia, 1989; pp. 672.
- Akihiko Kudo; Yugo Miseki; Heterogeneous photocatalyst materials for water splitting. Chemical Society Reviews 2008, 38, 253-278, 10.1039/b800489g.
- Vargaftic, N.B.. Handbook on Thermal Properties of Gases and Liquids (in Russian); Nauka: Moscow, Russia, 1972; pp. 720.
- Canan Acar, Ibrahim Dincer. 3.1 Hydrogen Production. In Comprehensive Energy Systems.; Ibrahim Dincer, Eds.; Elsevier: Netherlands, 2018; pp. 1-40.
- von Engel, A.. Ionized Gases; Clarendon Press: Oxford, UK, 1965; pp. 324.
- S Mededovic; Bruce Locke; Primary chemical reactions in pulsed electrical discharge channels in water. Journal of Physics D: Applied Physics 2007, 40, 7734-7746, 10.1088/0022-3727/40/24/021.
- Bruce R. Locke; Selma Mededovic Thagard; Analysis and Review of Chemical Reactions and Transport Processes in Pulsed Electrical Discharge Plasma Formed Directly in Liquid Water. Plasma Chemistry and Plasma Processing 2012, 32, 875-917, 10.1007/s11090-012-9403-y.
- Andressa Mota-Lima; Jailton Ferreira Do Nascimento; Osvaldo Chiavone-Filho; Claudio Augusto Oller Nascimento; Electrosynthesis via Plasma Electrochemistry: Generalist Dynamical Model To Explain Hydrogen Production Induced by a Discharge over Water. The Journal of Physical Chemistry C 2019, 123, 21896-21912, 10.1021/acs.jpcc.9b04777.
- Paul Rumbach; David M. Bartels; R. Mohan Sankaran; David B. Go; The solvation of electrons by an atmospheric-pressure plasma. Nature Communications 2015, 6, 7248, 10.1038/ncomms8248.
- Aleksey Yerokhin; Veta R. Mukaeva; Evgeny V. Parfenov; Nicolas Laugel; Allan Matthews; Charge transfer mechanisms underlying Contact Glow Discharge Electrolysis. Electrochimica Acta 2019, 312, 441-456, 10.1016/j.electacta.2019.04.152.
