1. Introduction
Electrical machines play a key role in modern industry and domestic appliances. With the requirement of reducing the consumption of fossil fuels and the emissions of carbon oxide, it is expected that most electricity will be generated by renewable energy and most drives will be electric motors. For example, electric motors are replacing the traditional internal combustion engines in cars, buses, trains, ships and even aircraft
[1][2][3][4][5][6][1,2,3,4,5,6]. The space and weight allowed in these vehicles are generally limited and they often operate with harsh conditions, such as high temperature and vibration. Therefore, one of the key issues for these applications is to investigate high-efficiency, high-power-density and high-reliability electric motors. For decades, researchers have been investigating various advanced electromagnetic materials for designing such high-performance electromagnetic devices, such as high-temperature superconductors
[7][8][7,8], ultra-thin electrical steel sheets
[9], soft magnetic composite
[10][11][12][10,11,12] and amorphous metal (AM) materials, specifically the amorphous ferromagnetic metal
[13][14][15][16][17][18][19][20][21][22][23][24][25][13,14,15,16,17,18,19,20,21,22,23,24,25]. Thanks to their advantageous properties of relatively low power losses at high frequency and very high saturation flux density, the AM materials appear to be excellent candidates as the core of high-power-density electromagnetic devices, such as high-speed electrical machines and high-frequency transformers.
AM materials, solid metallic materials and usually an alloy, have a disordered atomic-scale structure, which can also be called metallic glass and glassy metal. Amorphous ferromagnetic materials can be divided into several types based on their compositions, e.g., Fe-based, Ni-based and Co-based. Of these, the Fe-based types are commonly applied as machine cores thanks to their high saturation flux density and low cost. A number of companies supply the Fe-based AMs, such as Hitachi Metals Ltd., Japan, and Henan Zhongyuan Amorphous Technology Co. Ltd., China. Compared with traditional silicon steel, AM possesses the property of much lower power loss density, e.g., only about one tenth, making it an excellent candidate for high-frequency high-power-density electromagnetic devices. Furthermore, AM has reasonably high saturation magnetic flux density, e.g., much higher than that of ferrites commonly used in high-frequency transformers. Hence, AM magnetic devices can operate at reasonably high flux density and high frequency, leading to a small volume and high power density.
Therefore, AM has garnered strong interest as the core of high-efficiency, high-power-density electrical machines
[13][14][15][16][17][18][19][20][21][22][23][24][25][13,14,15,16,17,18,19,20,21,22,23,24,25]. In 1982, Johnson et al.
[13] investigated the application of low loss AM materials in electric motors and transformers. In 1989, Fukao et al.
[14] used AM to build the stator and rotor cores of a super-high-speed reluctance motor. At 48,000 rpm, the core loss of the AM machine is 80% lower than that of its silicon iron counterpart. In 1992, Jensen et al.
[15] proposed an axial-flux permanent magnet brushless DC motor, which has a tape-wound amorphous core and air-gap winding and shows the advantages of higher efficiency and lower costs compared to conventional machines. In 2008, Dehlinger et al.
[16] compared the stator core losses of claw-pole transverse flux machines with amorphous core and iron steel cores. Results indicated that machine efficiency and speed range can be increased by using amorphous cores. In 2011, Wang et al.
[17] developed a high-speed axial-gap ferrite permanent magnet motor with an AM stator, achieving an efficiency of 93% at 14,000 rpm.
In 2013, Kolano et al.
[18] designed a high-speed radial-flux permanent magnet brushless DC motor with an AM stator made of a Metglas 2605 SA1 amorphous ribbon, achieving a much smaller power loss than the silicon steel stator. In 2014, Fan et al.
[19] developed a high-power-density permanent magnet motor with AM stator, achieving a volume 31% smaller or power density 45% higher than that of a baseline motor. In 2015, Ertugrul et al.
[20] reported a high-speed induction electrical machine with an AM stator iron core, which is formed by laminating 0.025 mm 1k101 strips to the desired thickness and then annealing, dipping and solidifying the processes. In 2016, Tang et al.
[21] presented a review of the electrical machines with amorphous alloy cores and their key technologies, such as new topologies, processing, core losses and mechanical vibrations. In 2018, Simizu et al.
[22] developed a compact, high-speed (high frequency of over 1 kHz), high-power motor by applying low-loss amorphous magnetic materials. The core loss is very low, e.g., smaller than 3 W at the rated power, while that of the silicon steel machine will exceed 90 W.
In 2019, Li et al.
[23] presented the modeling and performance studies of high-speed synchronous reluctance motors considering the local effect of the AA core on the electromagnetic properties. In 2020, Ismagilov et al.
[24] reported the design, performance analysis, prototyping and experiment of a high-speed permanent magnet generator with the stator made by amorphous magnetic material for aerospace applications. In 2021, Fan et al.
[25] conducted the performance analysis and optimum design of a high-speed induction machine with an amorphous alloy iron core.
Although many achievements regarding developing AM electrical machines have been achieved, as in
[13][14][15][16][17][18][19][20][21][22][23][24][25][13,14,15,16,17,18,19,20,21,22,23,24,25], the results are still far from the material’s potentials. One of the major reasons is the lack of appropriate property models based on proper mechanism understandings of the material. Almost all the property data and models used for designing the electrical machines are obtained under one-dimensional (1D) alternating magnetic excitation
[26], and only a very small amount of work has been carried out for the AM properties under two-dimensional (2D) magnetization.
In the core of a rotating electrical motor or the T-joint of a three-phases transformer, the tip of magnetic flux density vector generally forms a 2D or even three-dimensional (3D) rotational irregular loop. It has been found that the magnetic material behaves very differently under the 1D alternating excitation and 2D/3D rotational excitation, and the conventional models cannot correctly predict the material properties under these irregular rotating flux density patterns
[27][28][29][30][31][32][33][34][27,28,29,30,31,32,33,34].
In summary, for achieving the best use of material potentials, the AM property characteristics should be investigated under the actual conditions that electromagnetic devices usually operate in. This papentryr aims to present an overview of the characterization of AM materials under 2D rotational magnetizations based on the authors’ research as well as other scholars’ relevant work in this area.
2. Measurement of Rotational Magnetic Properties of Amorphous Magnetic Materials
2.1. Measuring System of 2D Magnetic Properties
Since the first measurement of 2D rotational magnetic properties was reported by Baily in 1896
[27], a number of 2D rotational property measuring systems and techniques have been developed
[28][29][30][28,29,30]. Of these measurement systems, the square sample single sheet tester, which was developed by Brix et al.
[31], has proven to be the most favorable, thanks to its high control flexibility on rotating magnetic field patterns, outstanding uniformity of magnetic flux density distribution in the sample and, hence, high measurement accuracy.
Led by J. Zhu, the University of Technology Sydney (UTS) Magnetic Testing Group developed a square sample single sheet tester
[32], which has been used to measure different magnetic materials. This tester is cooperated via a computerized digital signal process system, and it is able to measure the
B-H relations as well as the core losses under 1D alternating fluxes in any specific direction, or 2D circularly and elliptical rotating fluxes with different axis ratios.
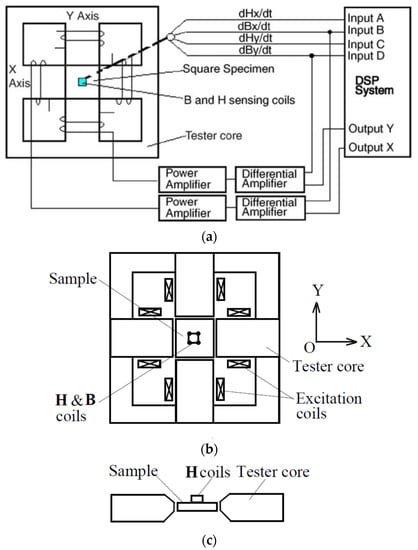
Figure 1 shows the schematic diagram of the square single sheet tester and the whole system. The tester contains yokes made up of laminated grain-oriented electrical sheets, and the yoke shapes were designed to form four wedge-type magnetic poles. Two excitation coil groups are wound around the X- and Y-axes, and each group has two coils, which are connected in series. A square sample of magnetic material is installed in the middle of the tester.
Figure 1. Principle diagram of the 2D rotating magnetic property test system: (a) schematic diagram, (b) single sheet tester for square sample and (c) positions of sample and H search coils.
The 2D magnetic field in the sample is produced with the currents flowing in the two sets of excitation coils discharged on X- and Y-axes, respectively. The excitation currents are provided by two power amplifiers. Through controlling the magnitudes, the phase angles and waveforms of the excitation currents, any 1D or 2D magnetic flux density vector can be produced, e.g., a 1D alternating flux density inclined at a specific angle from the X- or Y-axis, a circularly or elliptically rotational flux density or a flux density of any specified locus. Two dedicated differential amplifiers with low and high pass filters are used for the feedback control of the flux density components on the axes. The function generation and data acquisition are both realized by a PC-based digital signal processing system.
2.2. Material Sample for 2D Measurement
As shown in
Figure 1, a square material sample is placed in the tester center, where a magnetic field is generated by the X- and Y-axes excitation currents. In
our
esearchers' study
[33], the sample was fabricated by cutting the AMCC-320 amorphous core, which is composed of amorphous 1k101 strips. The square sample is of 50 mm length, 50 mm width and 0.86 mm thickness and consists of an amorphous strip stack of 25 μm in thickness. The stacking factor is about 0.85.
2.3. Measurement of 2D Magnetic Field
To acquire the
B-H relation and associated core loss, the magnetic flux density inside the sample and the magnetic field strength on the surfaces should be measured accurately. As shown in
Figure 1, the magnetic flux density and field strength in the sample can be acquired by the
B and
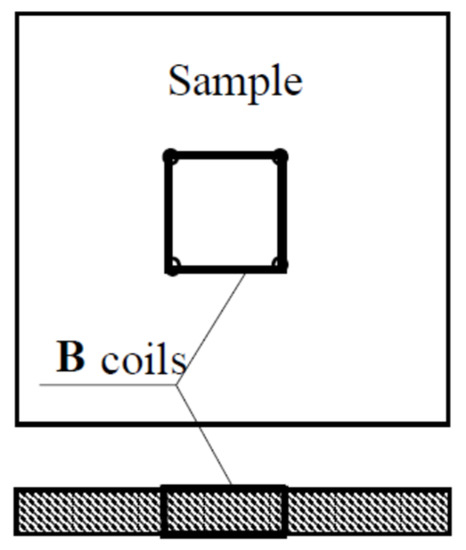
H sensing coils connected to the sample. Fifteen turns of enamel insulated copper wire of 0.1 mm in diameter are threaded through four small holes to form a B coil on each axis, as illustrated in
Figure 2. The perforation is tiny and has little effect on the magnetic field distribution inside the sample. For accurate measurement, the flux density should be uniformly distribution in the sample, which is realized by optimal design of the tester, particularly the shape and dimensions of the magnetic poles.
Figure 2.
Arrangement of 2D
B
coils.
The magnetic flux density on one axis can be computed by
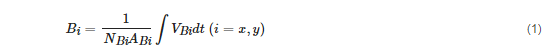
where
ABi is the cross-sectional area,
NBi is the turns number and
VBi the induced voltage across the terminals of the
B-coil on the axis.
The surface
H coils, as shown in
Figure 1c, are applied to measure the 2D magnetic field strength. According to the Ampere’s law, the field strength on the surface would be equal to that just inside the sample if there were no surface currents. The
H-sensing coils can be fabricated very thinly, and they can be attached on the sample surface and thus the true value of the field strength inside the sample can be acquired. The magnetic field strength component on one axis can be computed by
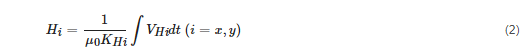
where
VHi is the induced voltage across the terminals of the
H-coil on the axis,
μ0 the permeability of air and
KHi the coil coefficient, which is determined by calibrating a solenoid as shown in
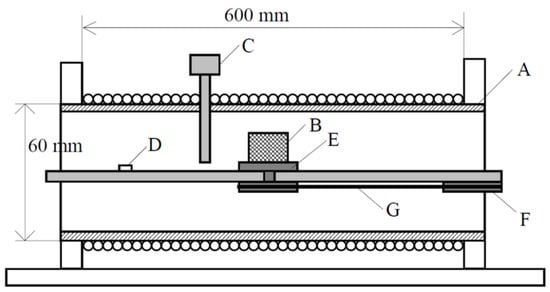
Figure 3, where A is the frame,
B is the
H coils to be calibrated, C is the Gauss meter probe, D is the connector for outputting the coil terminal voltage signals, E is the turn table for placing the coils and F and G are the wheel rubber bands for adjusting the coil orientation.
Figure 3.
Solenoid for calibrating
H
sensing coils.
It should be noted that this tester can also be used to measure the 1D alternating magnetic properties. When only the X-axis or Y-axis excitation current is applied, the
H and
B vectors are constrained in the X or Y direction, and the measured
B-H relation would be the traditional
B-H hysteresis loops.
The measurement of rotational magnetic properties is mainly conducted under the so-called circularly rotating magnetization, i.e., the excitation currents of the X- and Y- axes are controlled to form a rotating flux density vector of constant magnitude and speed. Sometimes, measurements under elliptically rotating magnetization are also carried out, e.g., with different ratios of the minor-axis to major-axis magnitudes of flux density. The magnetic properties are usually measured with various frequencies and various maximum flux densities.
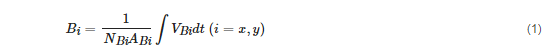 where ABi is the cross-sectional area, NBi is the turns number and VBi the induced voltage across the terminals of the B-coil on the axis.
The surface H coils, as shown in Figure 1c, are applied to measure the 2D magnetic field strength. According to the Ampere’s law, the field strength on the surface would be equal to that just inside the sample if there were no surface currents. The H-sensing coils can be fabricated very thinly, and they can be attached on the sample surface and thus the true value of the field strength inside the sample can be acquired. The magnetic field strength component on one axis can be computed by
where ABi is the cross-sectional area, NBi is the turns number and VBi the induced voltage across the terminals of the B-coil on the axis.
The surface H coils, as shown in Figure 1c, are applied to measure the 2D magnetic field strength. According to the Ampere’s law, the field strength on the surface would be equal to that just inside the sample if there were no surface currents. The H-sensing coils can be fabricated very thinly, and they can be attached on the sample surface and thus the true value of the field strength inside the sample can be acquired. The magnetic field strength component on one axis can be computed by
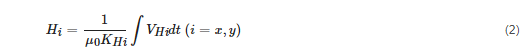 where VHi is the induced voltage across the terminals of the H-coil on the axis, μ0 the permeability of air and KHi the coil coefficient, which is determined by calibrating a solenoid as shown in Figure 3, where A is the frame, B is the H coils to be calibrated, C is the Gauss meter probe, D is the connector for outputting the coil terminal voltage signals, E is the turn table for placing the coils and F and G are the wheel rubber bands for adjusting the coil orientation.
where VHi is the induced voltage across the terminals of the H-coil on the axis, μ0 the permeability of air and KHi the coil coefficient, which is determined by calibrating a solenoid as shown in Figure 3, where A is the frame, B is the H coils to be calibrated, C is the Gauss meter probe, D is the connector for outputting the coil terminal voltage signals, E is the turn table for placing the coils and F and G are the wheel rubber bands for adjusting the coil orientation.