Physics and Technology of ITER: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Beatrix Zheng and Version 4 by Beatrix Zheng.

Like many of its fission counterparts, a fusion reactor will employ light water (i.e., H2O) to transfer heat from the Tokamak (i.e., plasma) to a boiler to produce the steam that will then drive conventional steam turbines to produce electrical power. ITER (“the way” in Latin) is not designed to produce electricity on a commercial scale; instead, it is intended to demonstrate sustained plasma burn and hence the feasibility of fusion power. Like most fission reactors, it too will be cooled by light water. The water will spend a certain time in the plasma radiation zone, in which the water will be subjected to intense, high-energy n and γ ionizing radiation. In the tritium breeding blanket containing LiOH, α radiation and tritons will be produced via the reaction 6Li3(1n0, 4He2)3H1, and these high Linear Energy Transfer (LET) radiation forms must be included in the source term for the radiolytically-generated species.

  • radiolysis of water
  • water-cooled reactor coolant circuits
  • ITER

1. Introduction

Interaction of the ionizing radiation with the coolant (water) results in the generation of a variety of radiolysis products, with those being identified to include e−aq, H, OH, H2O2, HO2, HO2-, O2, O2-, O22-, O−, O, H2, OH−, H+ and possibly others. These species are electroactive (i.e., they can participate in charge transfer reactions at metal/solution interfaces), thereby impacting corrosion processes and may lead to enhanced damage and to failure of components in the reactor primary coolant circuits by generating an excessively high electrochemical corrosion potential (ECP). Therefore, to understand and predict the impact of corrosion on the structural materials in the IBED PHTS of the ITER, the concentrations of these species must be known. While methods are available for measuring the concentrations of some of the radiolysis products (e.g., O2, H2, H2O2) in the laboratory, few techniques are presently available for measuring the concentrations of the more energetic species, such as e−aq, OH, HO2, O−, O, O2-, O22- and O2−, all of which are present at very low concentrations, in a plant environment, although absorption spectroscopic methods are used with great success in the laboratory and might be adapted to the field. However, from an electrochemical/corrosion viewpoint, there is no pressing need for knowing the concentrations of many of these highly energetic species. This is because the contribution that any given species makes to determining the ECP and the corrosion rate is roughly proportional to its concentrations because the rate of transport to the surface and the partial current density are often mass transport controlled and hence are proportional to the concentration. 

2. A Brief Primer on the Physics and Technology of ITER

One great advantage afforded by fusion as an energy source is demonstrated in Table 1, which summarizes the mass conversions for five different energy production technologies. The conversion values are calculated using Einstein’s energy/mass equivalence formula: ΔE=Δmc2, from the known energy yields, where ΔE is the energy produced upon conversion of a rest mass of Δm and c is the velocity of light (3 × 108 m/s). One sees from these data that the nuclear technologies—fission of 235U92 and the fusion of deuterium and tritium—are by far the most efficient in converting mass into energy, except for particle/antiparticle annihilation (e.g., e−-p+), for which the conversion efficiency is 100%. However, a cost-effective method for producing antiparticles (positrons) in sufficient amounts has yet to be devised to render this reaction to be of practical interest. It is also noted that of the technologies identified in Table 1, all but fusion and particle/antiparticle annihilation are currently contributing electrical energy to the national grid.
Table 1. Mass conversion factors for various energy production technologies.
Fuel Energy (Kw·h) Converted Mass (µg) % Mass Conversion
1 bbl of oil 576 23 1.64 × 10−8
1 ton of coal 2297 −92 0.92 × 10−8
100 ft3 of CH4 12 −0.48 2.37 × 10−8
1g of 235U92   −929 0.093
Fusion of 2D1 + 3T1   −0.019428 u 0.38
Annihilation e−-p+ 1.8219 × 10−31 u −1.8219 × 10−31 u 100
A second great advantage of fusion power is the limited amount of waste that is produced per unit of energy produced. Thus, according to an ORNL pamphlet, a small US city of 100,000 homes over 1 month requires 330,000,000 MJ of energy. If powered by coal, 150 railroad cars of bituminous coal are required that would produce 31,135 metric tons of CO2; 31 metric tons of CO; 67 metric tons of NOx; 365 tons of SOx; 411 metric tons of particulates; and 33 kg of formaldehyde, in addition to about 22 lbs (10 kg) of U and 57.6 lbs (26 kg) of Th. On the other hand, a fusion reactor would consume 5 kg of D (2H1) and T (3H1) and produce 4 kg of helium (4He2), for which a market already exists. Clearly, from an environmental impact viewpoint, fusion is the preferred technology. However, the production of high-energy neutrons necessarily means that neutron activation and transformation of some elements in the structural materials will occur. Accordingly, a radioactive disposal problem upon decommissioning will be faced, not unlike that in the decommissioning of a fission reactor. 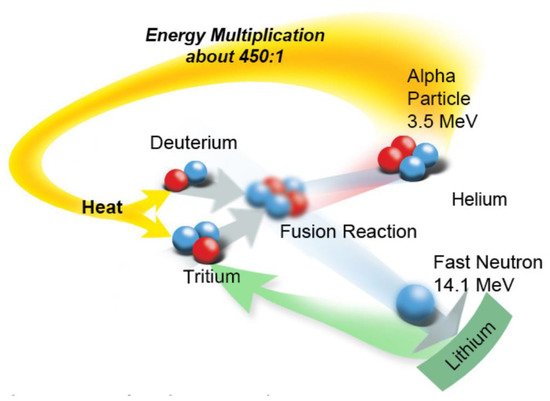A schematic of the D–T fusion reaction, which has the lowest “ignition temperature” of alternative fission reactions listed in Table 2, is presented in Figure 1. It is seen that fusion is envisioned to occur via the fusion of the two nuclei to produce an unstable quasi-nucleus, comprising two protons and three neutrons. This entity then decomposes to produce a high-energy alpha particle (4He2, 3.5 MeV) and a high-energy neutron (1n0, 14.1 MeV) with a concomitant loss of mass, in addition to γ-photons of 15–25 MeV. For fusion to occur, the D and T nuclei must approach one another to within a few diameters of the nucleus (a few femtometers), where the strong nuclear force can overcome coulombic repulsion and quantum mechanical tunneling of nucleons from one nucleus to the other can occur. This can only occur at very high kinetic energies that are sufficiently high that positively charged nuclei can approach one another to the requisite distance for tunneling to occur; that requires very high temperatures, of the order of 20 keV or more than 300,000,000 K. The energy released during the fusion process theoretically represents a 450:1 multiplication over the energy required to heat hydrogen nuclei to the fusion point [1].
Cmd 03 00028 g002 550
Figure 1. Schematic of the D–T fusion reaction. ©2018 US ITER.
Table 2. Mass conversion factors for fusion reactions between various isotopes of hydrogen.
Reaction Reaction Equation Initial Mass (u) Mass Change (u) % Mass Change
D–D 2D1 + 2D1 → 3He2 + 1n0 4.027106424 −2.44152 × 10−3 0.06062
D–D 2D1 + 2D1 → 3H1 + 1p1 4.027106424 −3.780754 × 10−3 0.09388
D–T 2D1 + 3T1 → 4He2 + 1n0 5.029602412 −0.019427508 0.3863
Attempts to harness fusion power have been underway since the 1950s, during which two basic approaches have evolved. The first, toroidal magnetic confinement fusion (MCF), is a Russian invention in which a low-density D–T plasma is confined magnetically in a toroidal chamber and is heated to fusion temperatures using extremely-high-density current and high-energy neutral particle and/or ion injection. In the second approach, inertial confinement fusion (ICF), or laser implosion, a mixture of D–T is contained within a small pellet, which is pulse irradiated from all sides using high-energy lasers, with the resulting adiabatic compression raising the temperature to the fusion threshold. Thus, these two fusion devices attempt to emulate the processes that power the sun and the stars—viz. the fusion of deuterium (2H1) and tritium (3H1): 2H1 + 3H1 → 4He2 (3.5 MeV) + 1n0 (14.1 MeV), as noted above, and that occur in thermonuclear weapons, respectively. However, several other fusion reactions involving the isotopes of hydrogen, as summarized in Table 2, are also possible. As noted above, the D–T reaction has the lowest “ignition temperature”, and hence this reaction is of the greatest interest in current fusion technology. It is also the reaction that results in the greatest conversion of mass into energy. Because this case uses tritium, which is not naturally occurring, tritium must be “bred” from some other nucleus, such as that described by the reaction 7Li3(1n0,4He2)3H1. On the other hand, if the D–D reaction was chosen, D is of plentiful supply in nature, as about 140 ppm of this isotope exists in natural water and the technology for its extraction is well developed. However, it requires a higher ignition temperature, and the mass conversion factor is not as attractive as the D–T reaction. In 1957, Lawson [2] derived the conditions that must be attained in the plasma for “breakeven” fusion (i.e., energy produced by fusion exceeding the energy input) as the “triple product”:
n T τ E ≥ 3 × 10 21   keV · s / m 3
where
where 
n
 is the plasma density (#/m
3
), 
T
 is the temperature (keV), and 
τE
 is the confinement time. The two approaches to controlled thermonuclear fusion differ in how these parameters are combined to achieve the Lawson energy balance. Thus, MCF aims at moderate 
n
 and 
T
 and a high 
τE
 to achieve the balance, while ICF makes use of high 
n
 and 
T
 combined with short 
τE to achieve the required breakeven condition. Furthermore, MCF seeks to produce a controlled, sustained “burn,” while ICF seeks to produce repetitive, miniature thermonuclear explosions. To date, MCF has come closest to attaining its stated goal.
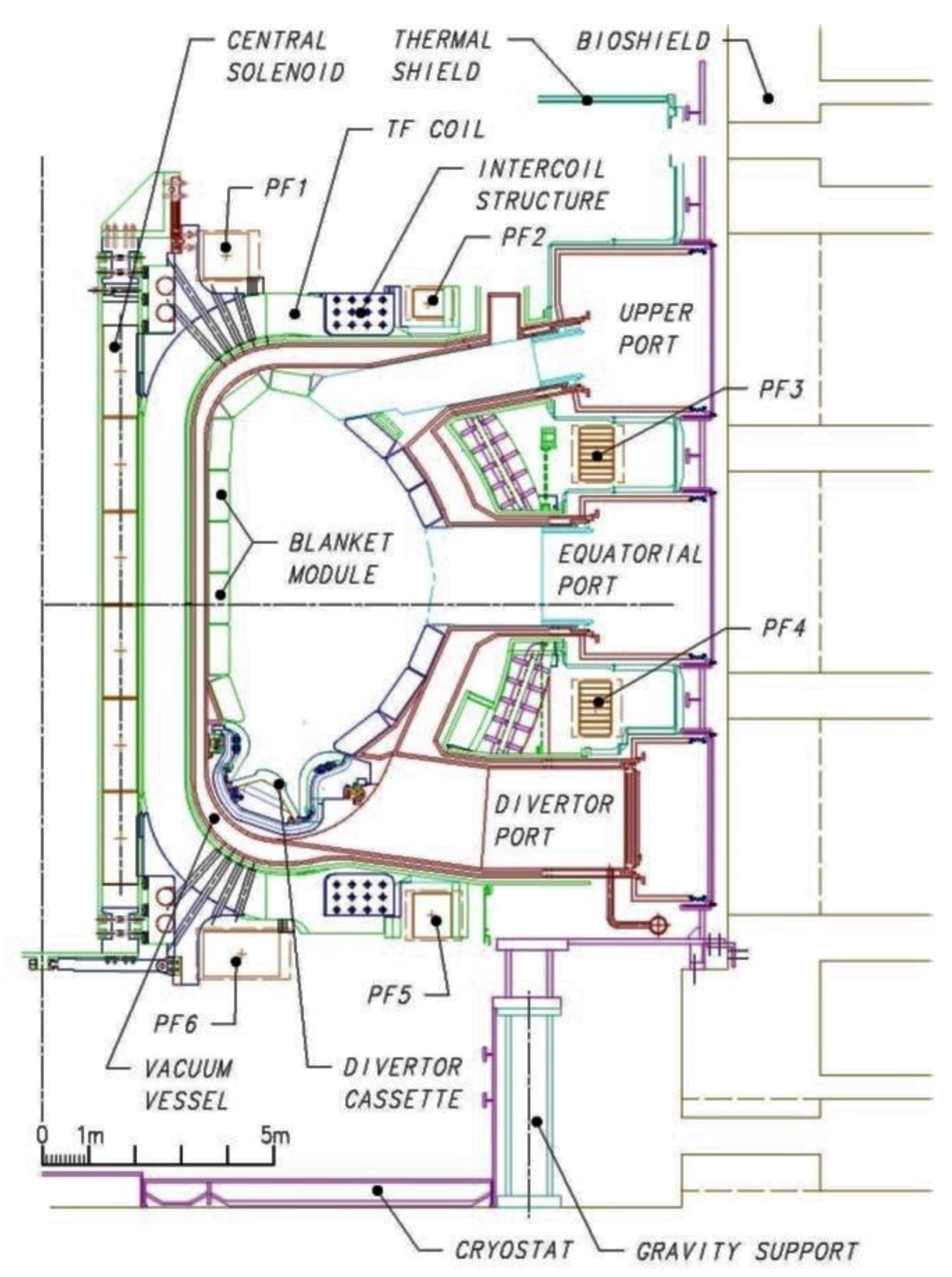
 to achieve the required breakeven condition. Furthermore, MCF seeks to produce a controlled, sustained “burn,” while ICF seeks to produce repetitive, miniature thermonuclear explosions. To date, MCF has come closest to attaining its stated goal. ITER is an example of the first approach (MCF) and is the logical extension of JET (Joint European Torus), which is operated in Oxford, England, UK. JET achieved a Q-value (i.e., the energy produced from fusion/input energy to heat the plasma) of 0.67 (16 MW out for 24 MW in), but ITER is expected to yield Q ≥ 10 (500 MW out for 50 MW in) over a sustained “burn” of about 550 s followed by a dwell period of 1250 s, to yield a repetition period of 1800 s (Table 3). Thus, ITER is a confined plasma device comprising a toroidal vacuum chamber and 5.3 T, Nb3Sn superconducting magnets that are designed to confine the hot plasma away from the walls.
Table 3. ITER Tokamak operating parameters (from ITER Technical Basis [3]).
Total Fusion Power 500 MW (700 MW)
Q-fusion power/additional heating power ≥10
Average 14 MeV neutron wall loading 0.57 MW m−2 (0.8 MW m−2)
Plasma inductive burn time ≥400 s (550 s, including ramp-up and ramp-down).
Plasma major radius (R) 6.2 m
Plasma minor radius (a) 2.0 m
Plasma current (Ip) 15 MA (17 MA a)
Vertical elongation @95% flux surface/separatrix (k95) 1.70/1.85
Triangularity @95% flux surface/separatrix (δ95) 0.33/0.49
Safety factor @95% flux surface (q95) 3.0
Toroidal field @6.2 m radius (BT) 5.3 T
Plasma volume 837 m3
Plasma surface 678 m2
Installed auxiliary heating/current drive power 73 MW b
a The machine can operate at a plasma current of up to 17 MA, with the corresponding parameters shown in parentheses, but with limitations on other parameters (e.g., pulse length). b In subsequent phases of operation, a total plasma heating power of up to 110 MW may be installed.
Figure 2 provides a schematic layout of ITER’s Tokamak building, with the scale being indicated at the bottom of the figure. The Tokamak, itself, is located within a reinforced concrete building. The effluent of greatest concern is tritium (3H1 → 3He2+ + 0e−1− + v¯e, t1/2 = 12.32 years, E = 18.6 keV) because it readily diffuses through steel pipe walls. Accordingly, tritium must be removed by various scrubbing devices. Moreover, 16N7 and 17N7, which are produced by the nuclear reactions 16O8(1n0,1p1)16N7 and 17O8(1n0,1p1)17N7, respectively, are a potential radiological contamination issue. Both are radioactive (16N7 → 16O8 + β + γ and 17N7 → 17O8 + β + ν¯e) and will be produced in the radiation zone. They will then be carried by the coolant to non-irradiated regions of the PHTS, where they will establish γ fields that will contribute to the main REM cost of operation, like that of a BWR operating on Hydrogen Water Chemistry (HWC). One critically important engineering consideration is the need for great rigidity of the tokamak structure, particularly the coils because they are subjected to high Lorentz forces produced by the circulating plasma in the magnetic field. Any distortion of the structure could affect the shape and stability of the plasma. Additional details on the structure of the Tokamak and the reactor building and related matters are given in [2][3][4][5][6][7][8][9][10][11][12][13][14][15][16][17][18][19][20][21][22][23][24][25][26][27][28][29][30][31].
Cmd 03 00028 g003 550
Figure 2. Cutaway view of the ITER fusion reactor (from ITER Technical Basis [3]). Note the size of the device in comparison with the human figure. ©2002 IAEA.
As noted above, the plasma is confined within the toroid by the magnetic field generated by the superconducting toroidal field (TF) coils and the central solenoid and is shaped by the six poloidal field (PF) coils (PF1 … PF6), which also protect the ports into the vacuum chamber, the blanket modules, the DIV cassette, and the control coils, as shown in Figure 3. The principal objective of this strong, shaped magnetic field is to keep the plasma away from the toroid walls. Since the plasma is at a temperature that corresponds well more than 300,000,000 K, no material, including beryllium, could withstand a “plasma strike”. Even if it did survive a transitory strike, the plasma would be contaminated that would interfere with the fusion process. Accordingly, the containment of the plasma is vitally important in magnetic confinement fusion technology.
/media/item_content/202209/63295c0bd8ba6cmd-03-00028-g004.png
Figure 3. Vertical cross section of the ITER Tokamak. TF = toroidal field; PF = poloidal field. The six poloidal field coils that are used to shape the plasma are depicted as PF1, PF2, …, PF6 (from ITER Technical Basis [3]). ©2002 IAEA.
Figure 4 illustrates the spatial arrangement of the PF coils and error field correction coils in the ITER Tokamak. The error correction coils are used to correct for any imperfections in the magnetic field symmetry that is shaped by the TF and PF coils (Figure 3 and Figure 4).
Cmd 03 00028 g005 550
Figure 4. Correction coil arrangement in the ITER Tokamak (PF coils and error field correction coils (from ITER Technical Basis [3]). ©2002 IAEA.
Table 3 summarizes the operating conditions envisioned for ITER. These are various design parameters and actual conditions that will be ascertained upon operation. Because the minimal Q value (Q = 10) is required for the demonstration of fusion power viability, the Q-value is particularly important. Anything short of this goal would require a major redesign of ITER and possibly development of an entirely new machine. Figure 5 provides the electron temperature, ion temperature, electron density, and helium density, and Figure 6 depicts the configuration of the plasma. Most important is the need to ensure that the extremely hot plasma does not contact the walls of the cavity because no material can withstand contact with the plasma without vaporizing. Preventing this contact is primarily the role of the six poloidal field coils (Figure 3), which also ensure plasma stability. The toroidal vacuum vessel is double-walled stainless steel and lined with Be-armored blanket modules, whose function is, amongst others, to breed tritium via 6Li3 + 1n0 → 3H1 + 4He2 and to shield the vacuum vessel wall from errant instabilities of the plasma.
Cmd 03 00028 g006 550
Figure 5. Profiles of electron temperature (Te), ion temperature (Ti), electron density (ne), and helium density (nHe) through the toroidal cavity (from ITER Technical Basis [3]). ©2002 IAEA.
Cmd 03 00028 g007 550
Figure 6. ITER nominal plasma configuration. The upper and lower “×” points are on different magnetic surfaces, defining two separatrixes, the primary one within the secondary one. The g1, g2, …, g6 refer to gaps whose sizes are control variables for plasma stability. The six poloidal field coils that are used to shape the plasma are depicted as PF1, PF2, …, PF6 (from ITER Technical Basis [3]). ©2002 IAEA.

References

  1. Hydrogen Fusion—An Opportunity for Global Leadership. Available online: https://usiter.org/sites/default/files/2018-06/hydrogen_fusion.pdf (accessed on 10 June 2022).
  2. Lawson, J.D. Some Criteria for a Power Producing Thermonuclear Reactor. In Technical Report; AERE: Harwell, UK, 1955.
  3. International Atomic Energy Agency. ITER Technical Basis; International Atomic Energy Agency: Vienna, Austria, 2002.
  4. Macdonald, D.D.; Engelhardt, G.R. Review and Assessment of Radiolysis in the TCWS IBED PHTS; OLI Systems, Inc: Cedar Knolls, NJ, USA, 2017.
  5. Hawryluk, R.J.; Campbell, D.; Janeschitz, G.; Thomas, P.; Albanese, R.; Ambrosino, R.; Bachmann, C.M.; Baylor, L.; Becoulet, M.; Benfatto, I.; et al. Principal Physics Developments Evaluated in the ITER Design Review. Nucl. Fusion 2009, 49, 065012.
  6. Shimomura, Y.; Spears, W. Review of the ITER Project. IEEE Trans. Appl. Supercond. 2004, 14, 1369.
  7. Wesson, J. Tokamaks, 2nd ed.; Oxford Engineering Science Series, No. 48; Clarendon Press: Oxford, UK, 1997.
  8. Roylston, K.; Radulescu, G.; van Hove, W.; Wilson, S.; Kim, S. Assessment of Activation on Level L3 of the Tokamak Building due to the ITER Tokamak Cooling Water System. Fusion Sci. Technol. 2019, 75, 458–465.
  9. Carloni, D.; Dell’Orco, G.; Babulal, G.; Somboli, F.; Serio, L.; Paci, S. Thermal Hydraulic Feasibility Analysis of the IBED-PHTS for ITER. Fusion Eng. Des. 2013, 88, 1709–1713.
  10. Billone, M.C.; Dienst, W.; Flament, T.; Lorenzetto, T.P.; Noda, K.; Roux, N. ITER Solid Breeder Blanket Materials Database; No. ANL/FPP/TM—263; Argonne National Lab: Lemont, IL, USA, 1993.
  11. Petrov, A.; Flanagan, G. Nuclear Chemistry of Water-Cooled Fusion Reactors: Issues and Solutions. In Proceedings of the International Conference on Water Chemistry of Nuclear Reactor Systems, Quebec City, QC, Canada, 3–7 October 2010.
  12. Romanelli, F.; Barabaschi, P.; Borba, D.; Federici, G.; Horton, L.; Neu, R.; Stork, D.; Zohm, H. A Roadmap to the Realization of Fusion Energy. In Proceedings of the 2013 IEEE 25th Symposium on Fusion Engineering (SOFE 2013), San Francisco, CA, USA, 10–14 June 2013; pp. 1–4.
  13. Petrov, A.; Berry, J.; Jonas, O.; Machemer, L. Selection of Water Chemistry for Successful Operation of Water-Cooled Fusion Machines. In Proceedings of the 14th International Conference on Environmental Degradation of Materials in Nuclear Power Systems, Virginia Beach, VA, USA, 23–27 August 2009.
  14. Bolt, H.; Barabash, V.; Federici, G.; Linke, J.; Loarte, A.; Roth, J.; Sato, K. Plasma Facing and High Heat Flux Materials–Needs for ITER and Beyond. J. Nucl. Mat. 2002, 307, 43–52.
  15. Barabash, V.; Ioki, K.; Merola, M.; Sannazzaro, G.; Taylor, N. Materials for the ITER Vacuum Vessel and In-Vessel Components–Current Status. Presented at the First Joint ITER-IAEA Technical Meeting on Analysis of ITER Materials and Technologies, Monte Carlo, Monaco, 23–25 November 2010.
  16. Ioki, K.; Akiba, M.; Barabaschi, P.; Barabash, V.; Chiocchio, S.; Daenner, W.; Elio, F.; Enoeda, M.; Ezato, K.; Federici, G.; et al. ITER Nuclear Components, Preparing for the Construction and R&D Results. J. Nucl. Mat. 2004, 329, 31–38.
  17. Elio, F.; Ioki, K.; Barabaschi, P.; Bruno, L.; Cardella, A.; Hechler, M.; Kodama, T.; Lodato, A.; Loesser, D.; Lousteau, D.; et al. Engineering Design of the ITER Blanket and Relevant Research and Development Results. Fusion Eng. Des. 1999, 46, 159–175.
  18. Sviatoslavsky, N.; Sawan, M.; Lulcinski, G.L.; Blanchard, J.; El-Guebaly, L.; Wittenberg, L. US Aqueous Salt Blanket for ITER. In Proceedings of the Presented at the US/Canada Workshop on Lithium Salt Blankets, Toronto, ON, Canada, 7–9 February 1989.
  19. Wikman, S.; Molander, A.; Öijerholm, J.; Eskhult, J.; Törnblom, O. Recent Development and Qualification of Materials for the European Contribution to ITER. ITR/P1-53, 23rd IAEA FEC. In Proceedings of the 23rd IAEA Fusion Energy Conference Daejeon, Daejeon, South Korea, 11–16 October 2010.
  20. Davis, J.W.; Smith, P.D. ITER Material Properties Handbook. Section 22. Data Bases and Data Nets. J. Nucl. Mat. 1996, 233–237, 1593–1596.
  21. Kalinin, G.; Matera, R.; Kawamura, H.; Rowcliffe, A.; Tavassoli, F. Structural Materials for ITER In-Vessel Component Design. J. Nucl. Mat. 1996, 233–237, 9–16.
  22. Belous, V.; Kalinin, G.; Lorenzetto, P.; Velikopolskiy, S. Assessment of the Corrosion Behaviour of Structural Materials in the Water Coolant of ITER Materials. J. Nucl. Mat. 1998, 258–263, 351–356.
  23. Lorenzetto, P.; Helie, M.; Molander, A. Stress Corrosion Cracking of AISI 316LN Stainless Steel in ITER Primary Water Conditions. J. Nucl. Mat. 1996, 233–237, 1387–1392.
  24. Kalinin, G.; Barabash, V.; Cardella, A.; Dietz, J.; Ioki, K.; Matera, R.; Santoro, R.; Tivey, R. Assessment and Selection of Materials for ITER In-Vessel Components. J. Nucl. Mat. 2000, 283–287, 10–19.
  25. Sato, K.; Mori, M.; Kataoka, Y. Evaluation of Oxygen/Hydrogen Production and Need for Degassing System. Priv. Commun. 2006.
  26. Yang, Q.; Dang, T.; Ying, D.; Wang, G.; Loughlin, M. Activation Analysis of Coolant Water in ITER Blanket and Divertor. Fusion Eng. Des. 2012, 87, 1310–1314.
  27. Kritsky, V.G.; Bobrov, Y.G.; Berezina, I.G.; Vasiljev, V.N.; Sadovnikova, L.B.; Shmanzar, O.P.; Korchemkina, O.G. Development of Water Radiolysis Computer Code for ITER Conditions. Priv. Commun. 2001.
  28. Christensen, H.; Molander, A.; Pettersson, S.-O.; Lassing, A.; Tomani, H. Studies of Water Radiolysis in the INCA Loop at 50 °C and 150 °C. Priv. Commun. 1996.
  29. Kalinin, G.; Barabash, V.; Fabritsiev, S.; Kawamura, H.; Mazul, I.; Ulrickson, M.; Wu, C.; Zinkle, S.J. ITER R&D: Vacuum Vessel and In-Vessel Components: Materials Development and Test. Fusion Eng. Des. 2001, 55, 231–246.
  30. Hirai, T.; Barabash, V.; Escourbiac, F.; Durocher, A.; Ferrand, L.; Komarov, V.; Merola, M. ITER Divertor Materials and Manufacturing Challenges. Fusion Eng. Des. 2017, 125, 250–255.
  31. Saji, G. Scientific Bases of Corrosion Control for Water-Cooled Fusion Reactors Such as ITER. In Proceedings of the 2012 20th International Conference on Nuclear Engineering collocated with the ASME 2012 Power Conference ICONE20-POWER2012, Anaheim, CA, USA, 30 July–3 August 2012.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback