The functioning of our universe and atomic is based on the oscillation of the particle itself and asymmetrically between matter and antimatter. This mechanism is a classical an-harmonic oscillator and uses a linear oscillation of the particle, where the energy can be represented by the graph of a potential well. In this potential well the alternation of energies ocurs between the kinetic energy and potential energy. This an-harmonic oscillation of the particle thus occurs through a gravitational oscillator (see "hole through the Earth simple harmonic motion"), followed by a singularity avoidance. Indeed the important kinetics of the particle leads to a singularity avoidance to pass over the supermassive black hole to plot the Higgs field/potential. The alternation of the particle at very high frequency generates by the principle of mass-energy equivalence in vacuum (E=mc²) a mass flux expressed by the quantum fluctuation determined by a scalar energy density. This scalar density represents for example the dark matter and the residues of the latter in the quantum vacuum. However a vectorial interpretation of the particle is possible as soon as its oscillation through the oscillator is really minimized before becoming a mass-energy equivalence flux. That represent the elements related to Einstein's Stress Energy Tensor. Here is the one of interpretation of quantum mechanics in relation to relativistic physics.
- anharmonic oscillator
- singularity avoidance
- gravitational oscillator
- oscillating universe theory
- oscillating model
- cyclic model
- Higgs
- universe
- theory
- kartazion
1. Introduction
The theory and the thought experiment of this paper followed by the observations and calculations already acquired, can lead us to the following reasoning developed below.
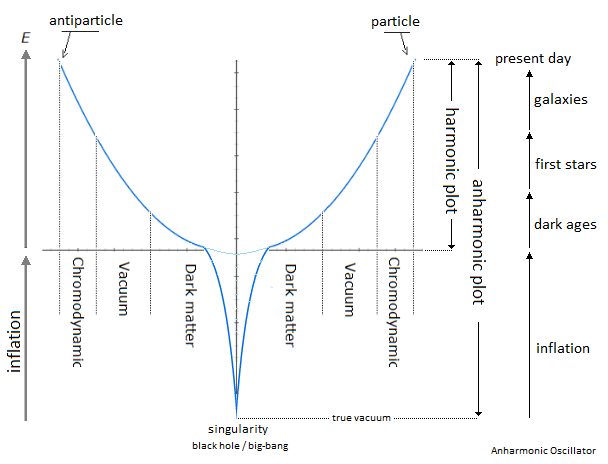 Figure 1. Once Upon a Time the Universe: Anharmonic Oscillator.
Figure 1. Once Upon a Time the Universe: Anharmonic Oscillator.
1.1. Foreword
The functioning of our universe and atomic is based on the oscillation of the particle itself [1][2]. This mechanism is a classical an-harmonic oscillator and uses a linear oscillation of the particle, where the energy can be represented by the graph of a potential well between Kinetic Energy and Potential Energy through a gravitational oscillator [3]. This an-harmonic oscillation of the particle thus occurs between matter and antimatter [4][5], followed by an avoidance of the gravitational singularity. This singularity avoidance [6][7][8] is of the supermassive black hole and/or big-bang type and is due to the high kinetics of the particle. On the other hand, and at total rest, this particle by its energy representation, is at the bottom of the potential well, at the lowest level, at the singularity, namely the total collapse of the universe which represents the state of true vacuum. But again, and through more sustained oscillation, a singularity avoidance occurs in contrast to the rest, and creates the levitation of the particle's energy to higher levels in its potential well. This singularity avoidance allows access to the current vacuum and is due to the kinetics and/or inertia of the particle. The role of the singularity in our model is fundamental and implies that it is the source and driver of the actual known result of quantum and cosmological fluctuations in relation to the motion of the particle. Indeed, the movement of the particle at very high frequency is interpreted by a flux expressed by the principle of mass-energy equivalence by scalar density. A representation related to Einstein's Stress Energy Tensor is then involved and also represent the mechanism of the cosmic inflation [9].
1.2. Harmonic Oscillator vs Anharmonic Oscillator
Harmonic Oscillator vs Anharmonic Oscillator. Indeed the difference is made here and is between the ideal harmonic layout and the absolut anharmonic layout of the energy captured in the potential well. In the case of singularity avoidance due to the high Kinetic Energy of the particle, cause that the plot of the curve of energy into the potential well tends towards a harmonic shape rather than an anharmonic one. In contrast an oscillation of the low-kinetic particle taking one by one the steps of the energy levels will trace the anharmonicity of the singularity through the shape of the potential well due to the singularity/inflation, because more exhaustively we can still imply the internuclear distance and the morse potential to give this characteristic of anharmonicity to the oscillator. Another characteristic of anharmonicity to the oscillator is that of the variation of speed uncontrolled and asymmetric of the particle gives an exactness of the scalar energy density along x-axis.
In the following illustration Figure 2, Figure 3 an integration of the gravitational singularity disturbs the harmonic shape of the potential well. The greater the kinetics of the particle in its oscillation, the more the shape of the potential well tends towards harmony by avoidance of the gravitational singularity. But if the kinetics of the particle are stopped, then the particle falls to the bottom of this gravitational singularity and traces the anharmonicity of the potential well. In the opposite case if the particle should to come out of its state of true vacuum to reach the higher energy levels, should correspond to the inflation for the universe and later that of the atom through another anharmonicity.
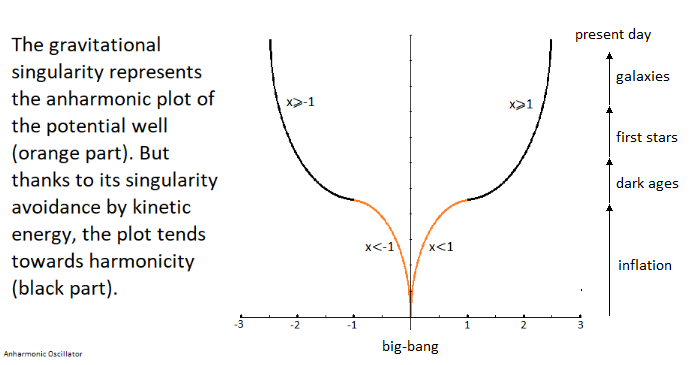
In a second part of this introduction, it is question of the singularity avoidance where the particle by its path traces the Higgs field. The Potential Energy is related to the depth of the gravitational singularity, because to pass over a black hole would have for value an enormous Potential Energy, and would plot with the representation of the energy of the particle the curve of the Higgs potential/field.
2. Gravitational Oscillator & Ideal Distribution of Energies
2.1. Gravitational Oscillator
Perpetual motion is a utopia. But in our case it represents an oscillation without mechanical constraint followed by the principle and the law of conservation of energy. In an interpretation of classical mechanics, the an-harmonic oscillation of the particle can be represented through a gravitational oscillator (Figure 4). It is initially used gravity to subject by attraction a movement to the particle. Here it is question of an oscillation of the particle which uses the same direction as the gravity vector. The acquisition of kinetic energy through potential energy under vacuum condition allows endless oscillation of the particle motion as long as its cycle of oscillation returns to the original gravitational source to continue its next cycle. Its description is based on the "Hole Through the Earth Example Simple Harmonic Oscillator" [10][11] which does not really have an example in French but which is nevertheless well studied for its principle. Here is a summary explanation: "If you drilled a hole in the axis of the Earth from pole to pole, and inserted a long, thin vacuum chamber into it, and then dropped an object into one end of that chamber, it would fall into the hole, picking up speed and it would move very fast when it reached the center of the Earth so it would continue until it reached the other pole where it would stop, then fall back "bounce" to come back and start again perpetually."
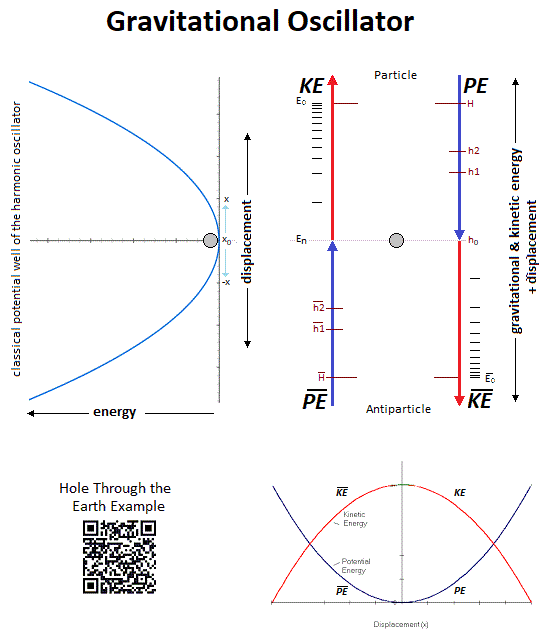 Figure 4. Gravitational oscillator and energy conservation between kinetic energy and potential energy SHO.
Figure 4. Gravitational oscillator and energy conservation between kinetic energy and potential energy SHO.
This linear gravitational oscillator in Figure 4 uses a particle of mass m oscillating vertically along the gravity vector G. This oscillator reprensent an simple harmonic motion (SHO) and the oscillation has two phases. The first is the falling phase of the particle with its Potential Energy PE and the second is the reverse phase which corresponds to the Kinetic Energy KE. It is from the center of the Earth that what is in Potential Energy is transformed into Kinetic Energy and is reversed at the level at the point of origine 0 or x=0.
2.2. Kinetic Energy & Potential Energy
In conclusion, for the gravitational oscillator presented in Figure 4, use the distribution of the two energies follows the following Figure 5 and operates according to the linear displacement of the particle, i.e. the alternation of the Potential Energy PE with the Kinetic Energy KE [12][13][14][15][16][17].
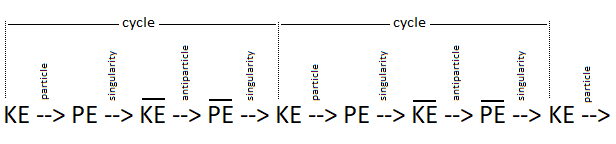 Figure 5. Oscillation cycle and alternation of Kinetic Energy and Potential Energy.
Figure 5. Oscillation cycle and alternation of Kinetic Energy and Potential Energy.
Potential Energy - Kinetic Energy = 0 In the following illustration in Figure 6, the integration of the gravitational singularity is not represented. If the energy in the potential well in Figure 6 has a curved shape, it represents the form of the amount of energy delivered to the particle according to x-axis. Which does not mean that the particle moves in a half-moon. The particle moves nice and well in a straight line in a radiative and linear way. In the Figure 6 we can distinguish three types of possible interpretations of states or/and energy paths due to displacement of the particle. In 1 and at the bottom of the harmonic potential well at x=0, we have the rest of the motionless particle or the ZPE (the lowest possible energy in a quantum system [18][19]). In 2 and with the Kinetic Energy applied to the particle, is at x=0 the maximum speed of the particle and drawing an energy path in a form of harmonic curve. In 3 it should be noted that the ideal trajectory of the energy path is the short circuit type between matter and antimatter and would trace a straight line, namely the shortest energy path in the potential well. This utopian energy path is actually not the conventional form of energy delivered to the particle. However, the annihilation of the electron/positron pair into a gamma photon should indicate this short-circuit type trajectory, and finally defined the characteristic of a boson. In our model the source [20] and the material existence as we know it, is based on the implication of the singularity of the big-bang type for the universe [21][22] and of the supermassive black hole type for the functioning for the galaxies [23][24][25][26], and other theoretical singularity as like that of the center of an atom [27]. In other words, the divergent evolution of the volume of the singularity is responsible for the presence of the matter that remains in its space-time. As gravity (Potential Energy) attracts the particle towards the core of the singularity, and who approaches it to fall inside, is then deflected by a energy barrier or additional energy to that of the total energy accumulated emanating from that same singularity . Indeed the singularity generates in 1 the gravitational attraction noted Potential Energy PE. In 2 we have the emanation of the additional energy complementary to the total Kinetic Energy given by scattering and/or astrophysical relativistic jet or Hawking radiation from singularity [28]. Moreover in 3 it should be noted that the singularity generates eletric charges on the particle [29]. In a more speculative and exotic definition and given our knowledge of the singularity in terms of gravitation followed by its ratio of time dilation, we could associate the center of the earth as such. Indeed for the particle which oscillates in the radiative oscillation from the center to the surface and vice versa, it becomes easy to imagine a gravitational singularity at the level of the Earth's core in the same way as the supermassive black hole in relation to its galaxy [30][31]. Singularity avoidance [6][7][8] is due to the high Kinetic Energy of the particle. At x=0 when the particle is going as fast as possible, its Kinetic Energy allows it not to fall at the bottom of the gravitational singularity Figure 7. Gravity (Potential Energy) corresponds to the matter attracted towards this singularity with the Kinetic Energy accumulating through Potential Energy. In our case it is simply a particle rather than a cluster of matter. A significant kinetics of the particle makes it possible to avoid the singularity,. and tThe path takes above this singularity by the particle energy determines the plot of the Higgs potential/field Figure 8. Indeed a barrier of potential barrier makes it possible to the particle to step over the singularity. An example of singularity avoidance with the Higgs implication is already done by scalar field definition [32], whereas for informathe ion the definition of vector boson is equally interpreted with or without Higgs [33][34]. In a second time the theoretical junction between the singularity avoidance and the Higgs field can be done by the enormous Potential Energy. Indeed, the Potential Energy being that in relation to the depth of the gravitational singularity gives the particle a much greater mass, or even a maximum value. The Higgs field and its potential are also well used to be able to represent the vacuum metastability [34][35][36][37][38] of the total density of the universe, as well as its interpretation as a quantum particle for its origin from mass. Singularity avoidance = enormous Potential Energy = Higgs mechanism = mass link We indicate a potential barrier around gravitational singularities. This barrier is due to the deformation of the gravitational space-time curvature by a massive object. At least a difference in level where the Potential Energy is felt around the mass object. Without Kinetic Energy, the inertia of the object (or particle) allows it to slide along the potential barrier that defines the path of the orbit around an even more massive object (geodesic and potential [3839]). In other words, the deformation of the space-time curvature due to an average object is felt at the level of the heights of the energies, and creates a barrier arounfd it Figure 10. The ZPE (Zero Point Energy) represents the initial perturbation of the particle at rest. At the quantum level this means that when the particle is at rest at the bottom of the harmonic potential well, the particle undergoes an oscillating disturbance. In cosmology this disturbance represents the inertial movement as an object orbiting around the gravitational singularity/massive object. In other words, the initial quantum disturbance of the Zero Point Energy corresponds to the cosmological movement of the object/particle located in the false vacuum in orbit around the gravitational singularity [3940]. Deformation also occurs for massive objects like stars. Vacuum metastability is determined by the amount of Kinetic Energy applied to the particle to trace its potential field in relation to the total energy density of the universe. If the Kinetic Energy of the particle is sufficient within the range of the energy condition allows to pass over the potential barrier, then singularity avoidance occurs; But during an attenuation of the kinetics of the particle or even a total stop of the inertia, that will cause by its amount of lower energy its fall towards the singularity and will reach the true vacuum and corresponds to the total collapse of the universe. However the vacuum metastability is under review [4041]. In other words, the inertial disturbance of the ZPE of the particle makes it possible to remain in the false vacuum by inertia, until a fictitious drop in this energy slows it down and then causes it to fall through a virtual slit to reach the another/middle/true/ vacuum. The energy applied to the particle which is at the bottom of the potential well in its state of true vacuum, should then be able to rise in higher energy levels through the anharmonicity of inflation. After acquiring enough energy and at the end of this inflation anharmonicity curve, energy dissociation It should be understood that in the event of a attempt to stop followed by slowing down of the kinetics of the particle due to the high potential barrier, the particle will then tend to pass through by the tunnel effect, instead of the singularity avoidance by the Higgs field and finds itself at the level of the black hole event horizon. This being said, this does not mean that the particle will finally reach true vacuum because the minimum kinetic/inertia was then send to the particle in order to be able to take the contuinity of its journey through the event horizon. This contrary scenario of the Kinetic Energy sent or subjected to the particle in order to be able to eject it again into the upper harmonic well of our vacuum, represent the singularity avoidance by the mechanism of Hawking radiation toward the upper harmonic energy well of our vacuum. This second Interpretation is to be considered as a singularity avoidance at the black hole event horizon (Figure 15) instead of the singularity avoidance over it by the Higgs field. Figure 15. Singularity avoidance at the black hole event horizon by quantum tunneling and Hawking radiation. In Figure 16 and according to the units of Planck, the number and the quantity of gravitons put end to end (point to point) along the vector of gravity G, then gives the total of the energy of gravitational potential. Each increment/decrement of the graviton, is obtained by adding or subtracting a linear total of energy quanta. The graviton/quanta can be represented by the size of the particle. It becomes easy to take into account the number of gravitons accumulated over the length of a ray noted in nm where this ray is parallel to the length of the vector G in order to be able to have a relationship between the number of gravitons in relation to the Potential Energy [5152][5253]. Most important is the role and the why of antimatter. As we can see the gravitational oscillator looks like a balanced perpetual motion without mechanical constraints. It is precisely on this side of the balance without mechanical constraint of the oscillation, that it makes that between Kinetic Energy and gravitation (Potential Energy) that the role of the antimatter becomes important. This allows the particle to simply bounce (due to deceleration from depletion of the particle's Kinetic Energy) to turn around using Potential Energy. There is therefore no impact of the particle that occurs in its cycle of oscillation. The Dirac Sea is a perfect representation of what the electron becomes in the depths of energy. Dirac predicts antimatter and the positron [5354]. We must therefore imply an anti-inflation followed by its anti-universe [5455][5556]. This therefore explains why we do not find the expected antimatter in the matter side of the universe, because antimatter is indeed found on the anti-universe side. In conclusion during a high energy collision, the annihilation of the pairs of particles make detect thanks to the gamma photon the presence of antimatter through the space-time. We understand that the symmetry breaking is located at x=0 at the level of the gravitational singularity. There is therefore a link between the Higgs potential and the symmetry breaking at x=0. If the charge and the parity CP are inter-changed following a linear movement of the particle either from bottom to top, then the arrow of time is perpendicular and flows for example from left to right. Still based on the oscillation of the particle itself, its presence distribution through its momentum and its position according to x (displacement) is asymmetrically arranged between matter and antimatter [5657]. Indeed the particle cannot be on matter and antimatter at the same time. Invariant transformation between vector and scalar interpretation of the mass-energy equivalence of the particle through the oscillator. The scalar interpretation of the particle represents the entropy of a very high frequency oscillation of the particle by its density occurring through the principle of mass-energy equivalence. But during a weak or almost non-existent oscillation, the particle is then represented by a vectorial direction during its movement. For example, a point mass object in the space-time reference frame is then represented by an orbital state vector during its movement around a star (conventional interpretation). But in the same proportion the particle in its dizzying oscillation can only be detected and measured by its energy density, and depending on the type of anharmonic oscillation its flow of entropy of the particle can be represented by an point mass object through a static value by a scalar value Figure 18. In conclusion, this leads to moving a scalar value of the same density vectorially. The goal being the invariance of mass-energy bound by the particle. In an inverse configuration when the particle is at rest gives a description of the first step of inflation directly related to Einstein's Stress Energy Tensor as soon as an enormous momentum of the particle takes on a scalar definition through a flux. The flux represents the maximum quantity of movement (momentum flux) through mass-energy equivalence (energy flux) during the start of inflation until its energy dissociation (formerly pressure). Whereas at rest while keeping its particle aspect by its vectorial representation is clearly defined by an almost motionless relation to x-axis, and the following anharmonic inflation in space-time is therefore represented by the internuclear distance levels up to energy dissociation. Based on the functioning of the mechanism of the anharmonic oscillator, involves during the movement of the particle, to make it go through different physical stages due to its high speed of displacement between matter and antimatter. We can also talk about the particle's energy flow to express the different cosmological or quantum states observed (Kasimir effect, etc.) [5758][5859]. The path of the particle is therefore linear and forms round trips. The path of the particle is therefore radiative. When the particle reaches a sufficient speed, a transformation into mass energy by the equivalence principle occurs. A small trace of this energy is found in vacuum and represents quantum vacuum energy. The successive addition of vacuum energy gives dark matter. In other words, the convergence of the energy flow (quantum fluctuation) of the quantum vacuum, in a more restricted space, close to the singularity, then in turn becomes dark matter [59][60][61][62][63]. At its opposite and the opposite of the singularity, there is matter expressed by quantum chromodynamics. Dark matter and quantum vacuum energy/quantum fluctuation is produced with the condition of the particle moving at very high speeds. Indeed the low frequency of oscillation of the particle through the oscillator, allows a vectorial interpretation as a point particle, while the high frequency of the particle through the principle of mass-energy of equivalence disappears from its shape punctual and is interpreted by a scalar density. Here in Figure 19 is an example of the absolute path taken by the particle. Here in Figure 20 is a simple potential well of energy to explain dark matter and quantum vacuum and quantum chromodynamics in relation to the oscillation of the particle: Dark energy corresponds to the increase in the size of the potential well. In the gravitational oscillator, the incrementation of the particle, that is to say a height of radiation greater than the previous height in the potential well, is produced by additional energy called dark energy; And which makes the particle advance further and further from its gravitational source. The example of a galaxy, where inside does not know an expansion of size in relation to its super massive black hole, uses a constant amount of Kinetic Energy in relation to gravity (Potential Energy). The increase in this Kinetic Energy that we have seen so far, then becomes dark energy, while it is only a amount of energy greater than the previous energy impulse. In other words, to move the particle further and further away from the singularity (i.e. big-bang) with the gravitational oscillator, more energy is needed. This extra amount of energy is dark energy [63][64][65][66]. Schrödinger's Cat is a thought experiment that illustrates the result of the quantum superposition paradox. If the particle is on A, then it cannot be on B. But at very high frequencies the particle has almost a 50% chance of being on A and B at the same time, hence the superposition state. If you were to randomly choose a position between A and B, then you would either have the particle in the hand (alive) or no particle in the hand, hence the cat experiment. In prediction, the quantum superposition states is at least straddling matter and antimatter before being detected on the matter side [66][67][68][69]. Quantum ChromoDynamics (QCD) would only be a duplication of the particle itself. It describes the mechanics of the quark superposition transition. In other words, quantum chromodynamics is the alternation of the particle itself to form the different combinations of quarks. QCD is the oscillation of the field which interferes with the particle in its convergence of the position towards its point of oringne 0 [27] and relating to the coupling constant (gauge coupling parameter). On the other hand during the material divergence due to the corelation of the particle on the surface of the energy sea, separating the quarks (which is only e.g. the alternating oscillation of the particle between 0 and 1 and 2 Figure 22) acts on the contrary of the coupling constant on asymptotic freedom [69][70][71][72][73][74][75]. It becomes obvious to make the link between entropy and plsma oscillation [75][76][77][78][79][80][81]. Figure 22. Quantum ChromoDynamics and coupling constant and asymptotic freedom. The gluon makes it possible to maintain the coherence of the quark in relation to the asymptotic freedom. But we can also understand that the gluon is more important and in terms of connection during the variation of the coupling constant towards its convergence at the level of the confinement of the quarks [8182][8283]. Here we understand through quantum chromodynamics, which represents correlated matter, that the general interaction field of quarks in its form of confinement, shapes objects as we perceive them (entropy [8384][8485]). In other words, the general field of the universe guides the quarks by forming the different atoms through the harmonic oscillator. This field is responsible for where the particle is located in the universe. Figure 23. The implication of radiation is simply due to the fact that the particle in its oscillation is linear. The direction of the work of the particle is along the vector of gravity, namely parallel to it. With the example of the lepton/baryon the gravitational oscillator has two types of radiation. First there is the vertical radiation, called fermionic, i.e. the normal oscillation of the particle from bottom to top and from top to bottom; And there is the horizontal radiation, or bosonic radiation which is not the oscillator. For the fermionic radiation and with the example of the lepton Figure 24 we have a movement of the particle from bottom to top in the oscillator which makes it possible to transport an electric charge to the surface of the sea of energy. In the opposite direction, either from top to bottom the particle goes down again in neutrino, or with a neutral charge. IOW this model, there is the link between Kinetic Energy and electric charge, and the neutrino follows the gravity (Potential Energy). Bosonic radiation, in its analogous interpretation, emits a kind of electric arc that occurs horizontally. Stimulated emission and photon emission in relation to the oscillation of the electron between its positions in orbitals in specific energy levels of the atom Figure 25. The quantum atom is basically composed of quantum leap of the particle between matter and anti-matter. These jumps correspond to the Bottom-up oscillation and have an almost instantaneous value. They can for example be of the order of a few million or a few billion jumps in a nanosecond. The Pauli exclusion is always respected because there is only one particle present per atom created by a reiteration of its position in different and unique states. In Figure 27 the neutrino represents the particle without electric charge and is electrically neutral. The neutrino has a direct relationship with that of Potential Energy [8586]. On the contrary, when the particle is emitted by Kinetic Energy, the latter carries an electric charge. The dosage of the Kinetic Energy through the anharmonic oscillator with the internuclear distance makes it possible to deliver the amount of energy necessary in term of electron-volt. Reiteration in series of neutron N and proton P to be able to define the mathematical simulation of the pure quantum atom. The pure quantum atom is non-isotropic. It corresponds to the two choices which is that of the neutron N or the proton P. The reiteration in a series of Neutrons N followed by Protons P (same number of N as of P) is a pure atom. Each line in Figure 29, Figure 30, Figure 31 with the "atom signature" represents the path of the particle to the singularity by neutrinos as it descends, and responsible for the electrical charges generated as it ascends. The line spacing corresponds to the "atomic signature" as a function of the energy delivered by the particle. The smaller the energy in electron volts, the larger the line spacing. The absence of lines indicates that there are no particles in the field to be studied. In conclusion and by the linear radiation of the particle due to its oscillation, can build a structure by reiteration of its position and this in several places Figure 32. Indeed the alternation at very high frequency of the particle between its point of origin 0 and the constitutive structure, makes it possible to be able to create any object. Favoring the ironing of the particle on precise positions to the detriment of other positions makes it possible to be able to create more or less heavy objects Figure 33. Here is the example of a small JavaScript program [8687] where its interest is to be able to put the evidence of a duplication of a particle in several places. Its operation is as follows: oscillating or alternating at the speed of light a 5mm particle from position A to position B spaced 10cm apart, would beseen as two visible points as a fixed and static appearance. The most important thing is to be able to mark a certain stop on each position of A and B, and to travel between them almost instantaneously. Virtual particles are very well studied in Quantum Field Theory. Here [8788] is the synoptis and the interpretation in image of what is a production of virtual particles. Indeed we can see there an extrapolation from the particle to the antiparticle as naturally as an an-harmonic oscillation [8889]. The constitution of the physical laws as well as the result of this chaos of the universe until us suggests that it was premeditated. The name of the main theory described in this paper is called Kartazion. Kartazion model of quantum physics and cosmological according to Arnaud Andrieu.2.3. Energy Path in the Potential Well
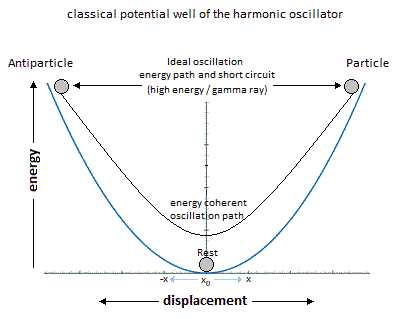 Figure 6. Potential well and energy path.
Figure 6. Potential well and energy path.3. Source of Quantum Fluctuations & Gravitational Singularity
3.1. Speculative Singularity
4. Singularity Avoidance & Higgs Boson
4.1. Singularity Avoidance
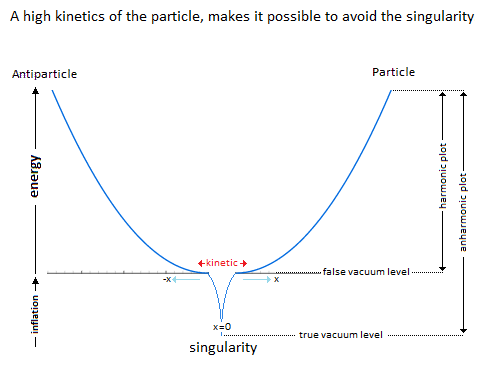
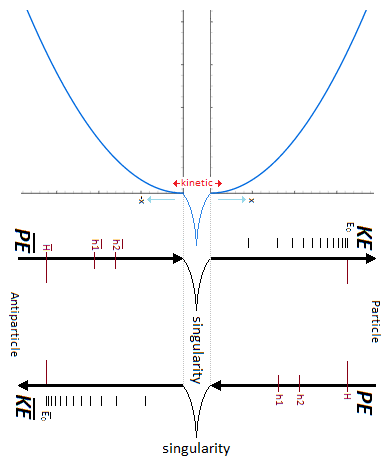 Figure 7. Gravitational oscillator and singularity avoidance by high kinetic of the particle.
Figure 7. Gravitational oscillator and singularity avoidance by high kinetic of the particle.4.2. Singularity Avoidance through Higgs Boson
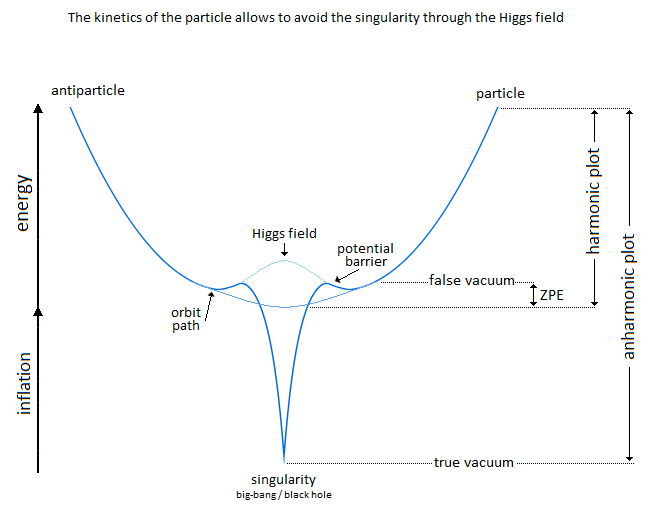 Figure 8. Gravitational oscillator and singularity avoidance through Higgs filed.
Figure 8. Gravitational oscillator and singularity avoidance through Higgs filed.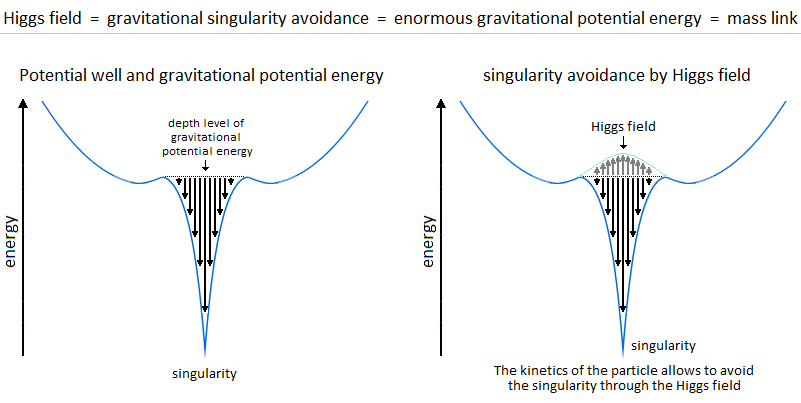 Figure 9. Potential Energy in relation to the depth of the gravitational singularity and the Higgs potential.
Figure 9. Potential Energy in relation to the depth of the gravitational singularity and the Higgs potential.5. Orbit, Inertia, ZPE & Potential Barrier
5.1. Potential Barrier
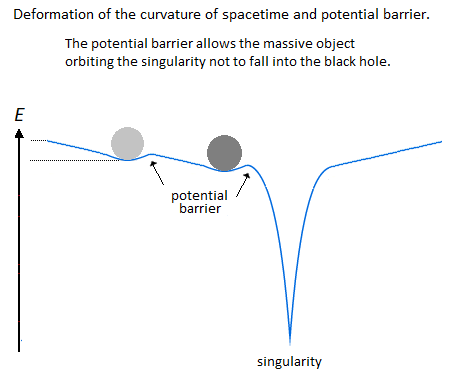 Figure 10. Singularity avoidance by inertia and orbit path (geodesic).
Figure 10. Singularity avoidance by inertia and orbit path (geodesic).5.2. The Zero Point Energy
6. Vacuum Metastability
6.1. Vacuum Metastability
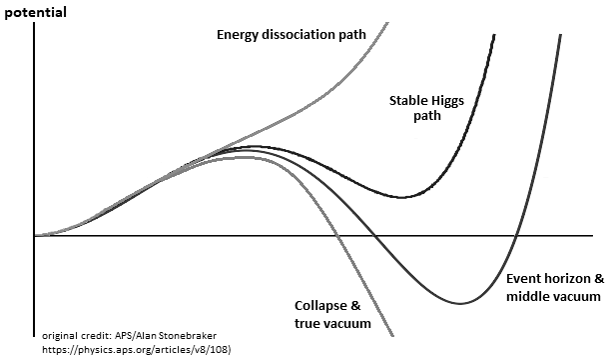
6.2. Tunnel Effect
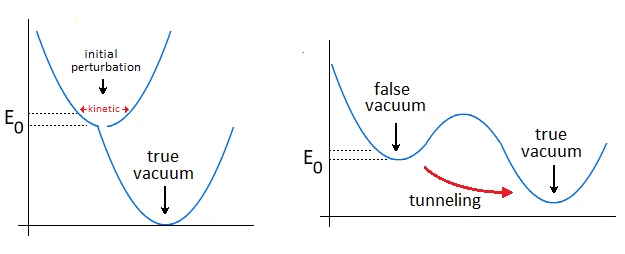
6.3. Bifurcation & Energy Dissociation
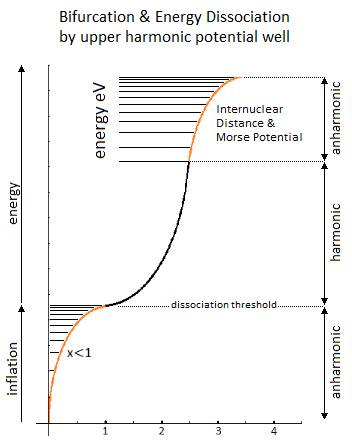 Figure 13. Bifurcation & Energy Dissociation by upper Potential Well & Internuclear Distance & Morse Potential & Ionic Bond.
Figure 13. Bifurcation & Energy Dissociation by upper Potential Well & Internuclear Distance & Morse Potential & Ionic Bond.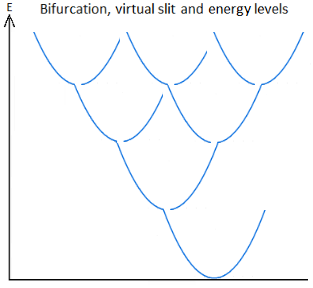
7. Second Interpretation of Singularity Avoidance
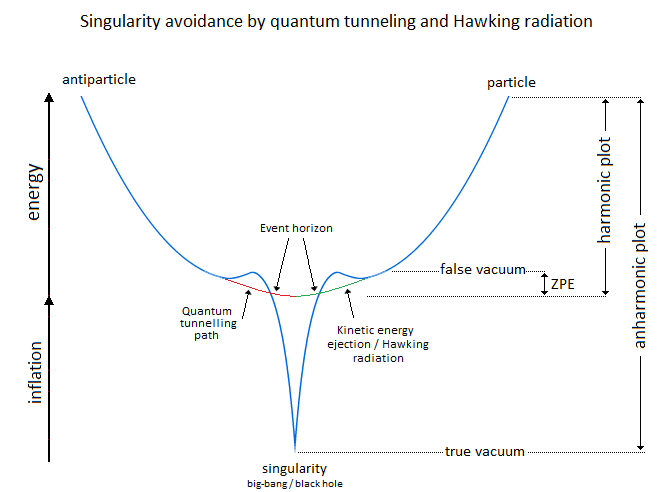
8. Graviton & Potential Energy
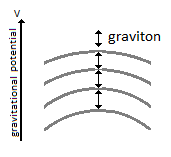 Figure 16. Relationship between number of gravitons in relation to the Potential Energy.
Figure 16. Relationship between number of gravitons in relation to the Potential Energy.9. Asymmetry Matter Antimatter
10. Symmetry Breaking CP & Arrow of Time T
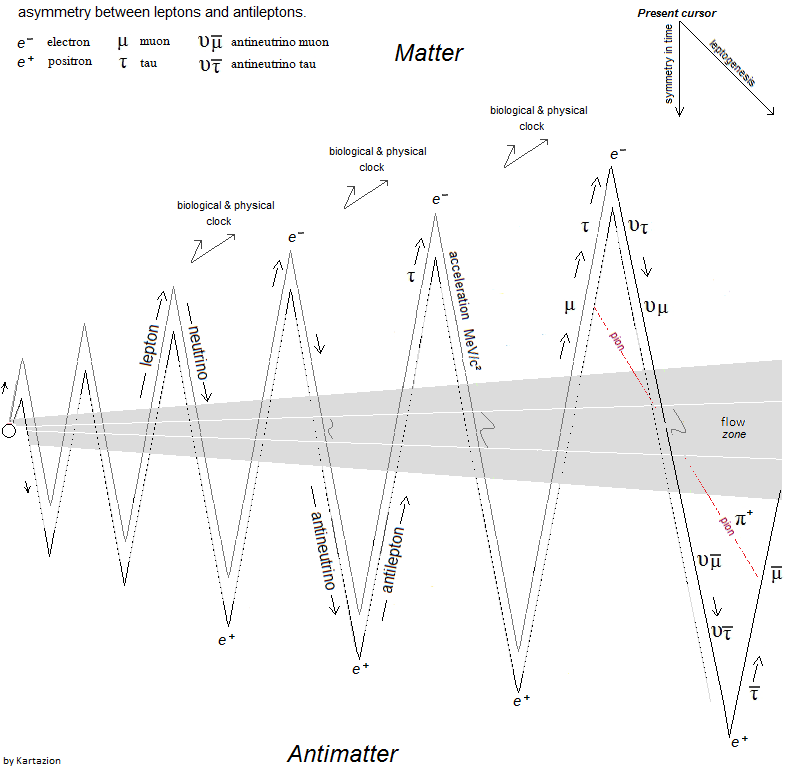
11. Scalar & Vector Interpretation of the Particle
11.1. Invariant Transformation
 Figure 18. Anharmonic oscillation & probability of the Particle by scalar densiy.
Figure 18. Anharmonic oscillation & probability of the Particle by scalar densiy.11.2. Cosmic Inflation & Stress Energy Tensor
12. Path of the Particle, Quantum Fluctuation & Dark Matter
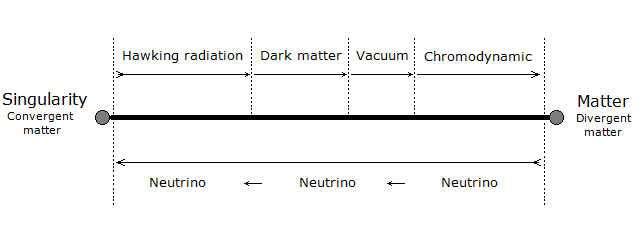 Figure 19. Absolute path taken by the particle through the oscillation.
Figure 19. Absolute path taken by the particle through the oscillation.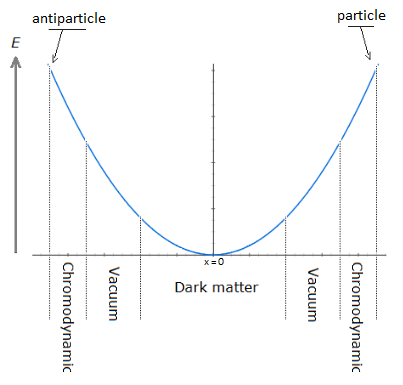
13. Dark Energy
14. Quantum Superposition
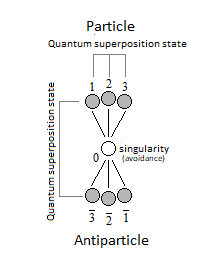 Figure 21. Combination of quantum superposition states.
Figure 21. Combination of quantum superposition states.15. Quantum ChromoDynamics
15.1. Coupling Constant & Asymptotic Freedom
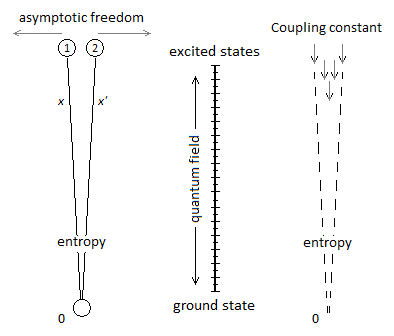
15.2. Gluon & Quark
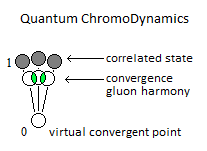
16. Particle Radiation & Boson
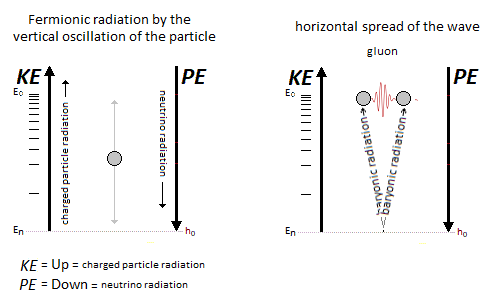 Figure 24. Fermionic radiation and Bosonic radiation.
Figure 24. Fermionic radiation and Bosonic radiation.16.1. Stimulated Emission & Boson Emission
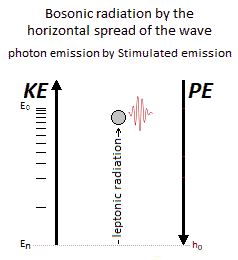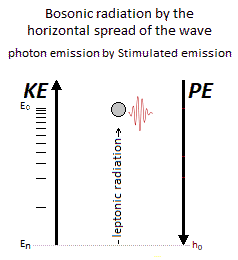 Figure 25. Stimulated emission and photon emission in relation to its orbitals.
Figure 25. Stimulated emission and photon emission in relation to its orbitals.17. Atom & Quantum Atom
The atomic model described in Figure 26 represents the synopsis of the logical sequence of the oscillation mechanism of the particle through to the anharmonic characteristic. Its oscillation is located between matter and antimatter, where between two its acceleration would then be almost instantaneous by singularity avoidance. We can see by the anharmonic oscillator the classic version of the internuclear distance followed by the morse potential to be able to give the energy wanted to the particle.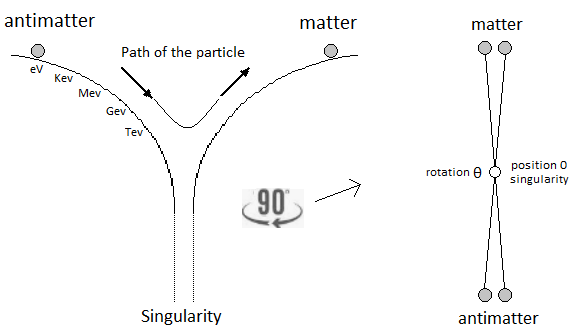 Figure 26. The anharmonic characteristic of the oscillator by the internuclear distance follow by the morse potential, makes it possible to give by the quantity of kinetic energy received from the particle its mass in term of electron-volt.
Figure 26. The anharmonic characteristic of the oscillator by the internuclear distance follow by the morse potential, makes it possible to give by the quantity of kinetic energy received from the particle its mass in term of electron-volt.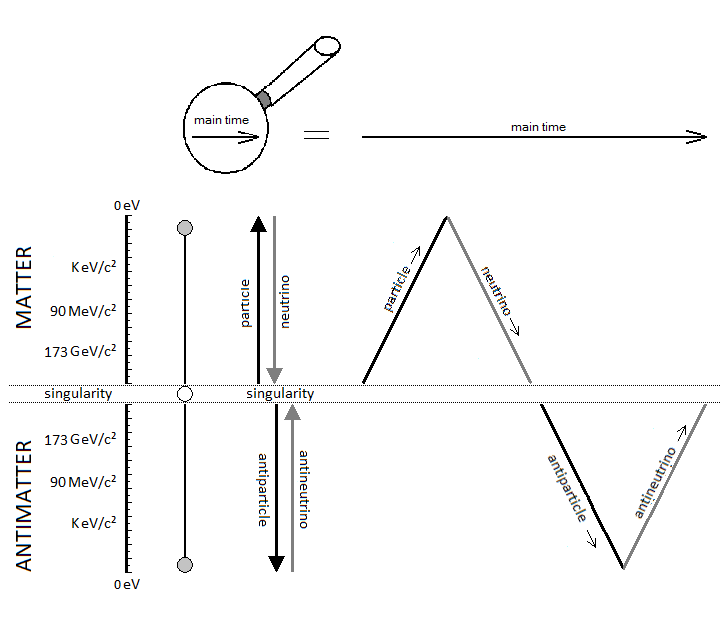
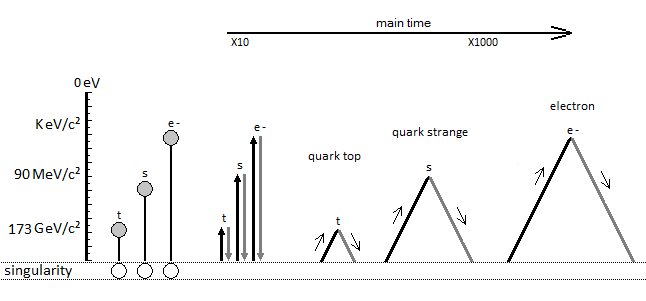
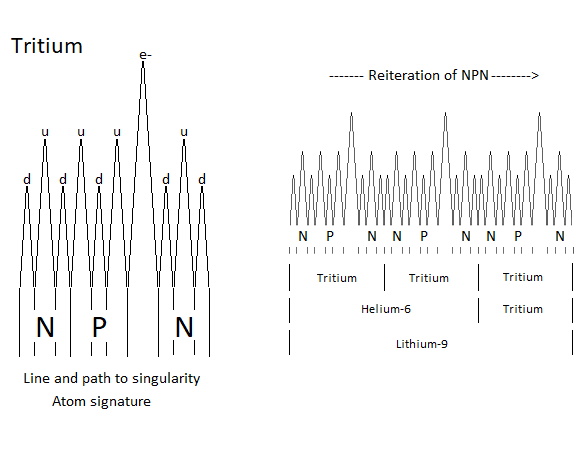
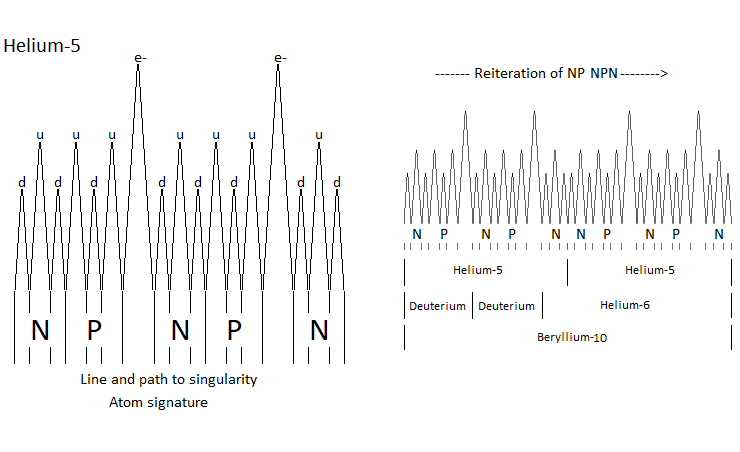
Thanks to the principle of reiteration, and if you had the choice between neutron and proton, the probability of finding an N neutron followed by a P proton like NP or NPN in the atomic nuclei is substantial. Which brings us, and in relation to the atomic signature, to the conclusion of a composition rich in Deuterium, Tritium and Helium 4-5-6 (Figure 29, Figure 30, Figure 31).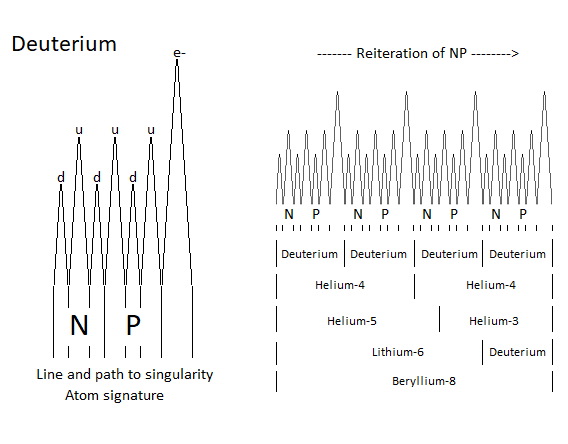
18. Example Structures & Conclusion
18.1. Example Structures
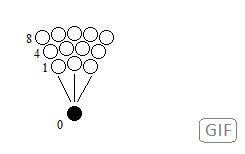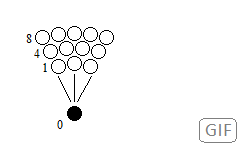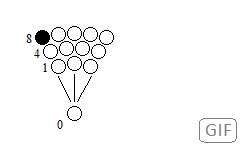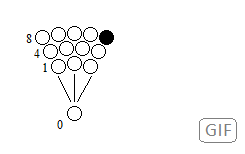 Figure 32. Reiteration by oscillation of the particle in its position in several places.
Figure 32. Reiteration by oscillation of the particle in its position in several places.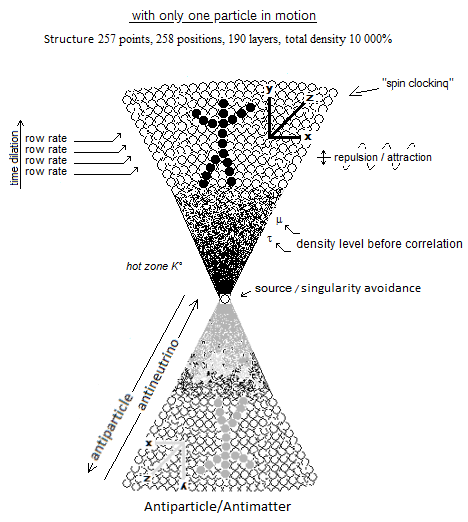 Figure 33. Example structure of the oscillation of the single particle. The field that guides the particle is responsible for the elements known.
Figure 33. Example structure of the oscillation of the single particle. The field that guides the particle is responsible for the elements known.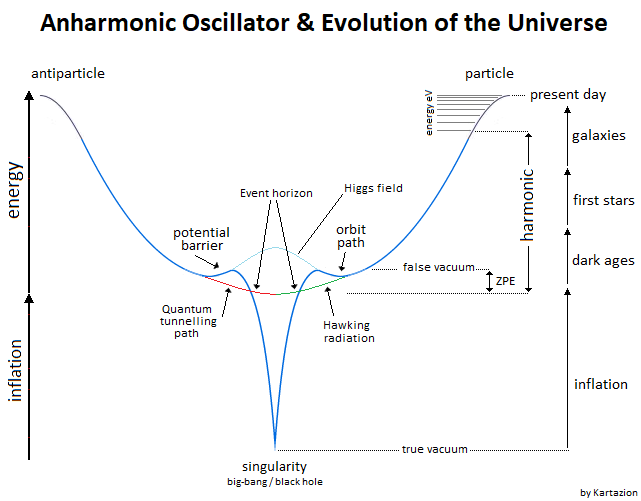 Figure 34. Anharmonic Oscillator and the evolution of the universe.
Figure 34. Anharmonic Oscillator and the evolution of the universe.18.2. Simulation by Programming
18.3. Virtual Particles
18.4. Conclusion
References
- John. D. Barrow; Mariusz. P. Dabrowski; Oscillating universes. Monthly Notices of the Royal Astronomical Society 1995, 275, 850-862, 10.1093/mnras/275.3.850.
- Yun-Song Piao; Yuan-Zhong Zhang; Inflation in oscillating universe. Nuclear Physics B 2005, 725, 265-274, 10.1016/j.nuclphysb.2005.07.021.
- Itzhak Goldman; Nathan Rosen; Gravitation Theory and Oscillating Universe. Physical Review D 1972, 5, 1285-1287, 10.1103/physrevd.5.1285.
- Roy A. Briere; LHCb Collaboration; Observing Matter-Antimatter Oscillations. Physics 2013, 6, 1-3, 10.1103/physics.6.26.
- M.K. Parida; Natural mass scales for observable matter-antimatter oscillations in SO(10). Physics Letters B 1983, 126, 220-224, 10.1016/0370-2693(83)90594-4.
- Iberê Kuntz; Roberto Casadio; Singularity avoidance in quantum gravity. Physics Letters B 2020, 802, 135219, 10.1016/j.physletb.2020.135219.
- V Husain; Singularity avoidance, lattices, and quantum gravity. Canadian Journal of Physics 2008, 86, 583-586, 10.1139/p07-201.
- J Brunnemann; T Thiemann; On (cosmological) singularity avoidance in loop quantum gravity. Classical and Quantum Gravity 2006, 23, 1395-1427, 10.1088/0264-9381/23/5/001.
- Paul R. Anderson; Carmen Molina-París; Emil Mottola; Short distance and initial state effects in inflation: Stress tensor and decoherence. Physical Review D 2005, 72, 043515, 10.1103/physrevd.72.043515.
- Andrew J. Simoson; Falling down a Hole through the Earth. Mathematics Magazine 2004, 77, 171, 10.2307/3219113.
- Journey through the center of the Earth . Hyperphysics. Retrieved 2022-7-28
- C. A. Coulson; R. P. Bell; Kinetic energy, potential energy and force in molecule formation. Trans. Faraday Soc. 1945, 41, 141-149, 10.1039/tf9454100141.
- Robert C. Hilborn; Galilean Transformations of Kinetic Energy, Work, and Potential Energy. The Physics Teacher 2019, 57, 40-43, 10.1119/1.5084927.
- William D. Harkins; The Change of Molecular Kinetic Energy into Molecular Potential Energy. Proceedings of the National Academy of Sciences 1919, 5, 539-546, 10.1073/pnas.5.12.539.
- R. H. Schwendeman; Comparison of Experimentally Derived and Theoretically Calculated Derivatives of the Energy, Kinetic Energy, and Potential Energy for CO. The Journal of Chemical Physics 1966, 44, 2115-2119, 10.1063/1.1726989.
- R. F. Snider; Conversion between kinetic energy and potential energy in the classical nonlocal Boltzmann equation. Journal of Statistical Physics 1995, 80, 1085-1117, 10.1007/bf02179865.
- Rory O. Rafi Y. Thompson; Efficiency of conversion of kinetic energy to potential energy by a breaking internal gravity wave. Journal of Geophysical Research 1980, 85, 6631, 10.1029/jc085ic11p06631.
- Timothy H Boyer; Quantum zero-point energy and long-range forces. Annals of Physics 1970, 56, 474-503, 10.1016/0003-4916(70)90027-8.
- Hristu Culetu; The zero point energy and gravitation. arXiv 2004, 1, 1-18, 10.48550/arXiv.hep-th/0410133.
- Jevgenijs Kaupuzs; Energy fluctuations and the singularity of specific heat in a 3D Ising model. Second International Symposium on Fluctuations and Noise 2004, 1, 480-491, 10.1117/12.546493.
- John D. Barrow; Robert J. Scherrer; Constraining density fluctuations with big bang nucleosynthesis in the era of precision cosmology. Physical Review D 2018, 98, 043534, 10.1103/physrevd.98.043534.
- M. Giovannini; M. E. Shaposhnikov; Primordial Magnetic Fields, Anomalous Matter-Antimatter Fluctuations, and Big Bang Nucleosynthesis. Physical Review Letters 1998, 80, 22-25, 10.1103/physrevlett.80.22.
- Kouji Nakamura; Shigelu Konno; Yoshimi Oshiro; Akira Tomimatsu; Quantum Fluctuations of Black Hole Geometry. Progress of Theoretical Physics 1993, 90, 861-870, 10.1143/ptp.90.861.
- Jianwei Mei; Fluctuating black hole horizons. Journal of High Energy Physics 2013, 2013, 195, 10.1007/jhep10(2013)195.
- Tomohiro Takahashi; Jiro Soda; Hawking radiation from fluctuating black holes. Classical and Quantum Gravity 2010, 27, 1-35, 10.1088/0264-9381/27/17/175008.
- Gilad Gour; A J M Medved; Thermal fluctuations and black-hole entropy. Classical and Quantum Gravity 2003, 20, 3307-3326, 10.1088/0264-9381/20/15/303.
- The hydrogen atom with an origin centred singularity . ResearchGate. Retrieved 2022-7-28
- Don N Page; Hawking radiation and black hole thermodynamics. New Journal of Physics 2005, 7, 203-203, 10.1088/1367-2630/7/1/203.
- Ondřej Kopáček; Vladimír Karas; Near-horizon Structure of Escape Zones of Electrically Charged Particles around Weakly Magnetized Rotating Black Hole. II. Acceleration and Escape in the Oblique Magnetosphere. The Astrophysical Journal 2020, 900, 119, 10.3847/1538-4357/ababa8.
- A Marasco; G Cresci; L Posti; F Fraternali; F Mannucci; A Marconi; F Belfiore; S M Fall; A universal relation between the properties of supermassive black holes, galaxies, and dark matter haloes. Monthly Notices of the Royal Astronomical Society 2021, 507, 4274-4293, 10.1093/mnras/stab2317.
- Andrew King; The Supermassive Black Hole—Galaxy Connection. null 2013, 49, 427-451, 10.1007/978-1-4939-2227-7_21.
- Luca Fabbri; Black Hole singularity avoidance by the Higgs scalar field. The European Physical Journal C 2018, 78, 1028, 10.1140/epjc/s10052-018-6505-6.
- V. Aldaya; Manuel Calixto; Francisco F. López Ruiz; A QUANTIZABLE MODEL OF MASSIVE GAUGE VECTOR BOSONS WITHOUT HIGGS. Modern Physics Letters A 2009, 24, 2731-2740, 10.1142/s0217732309032034.
- Marcelo Gleiser; Metastability in the early Universe. Sally Dawson; T. Han; Wai Kin Lai; Adam Leibovich; I. Lewis; Resummation effects in vector-boson and Higgs associated production. Physical Review D 201990, 42, 3350-3361, 10.1103/physrevd.42.3350.2, 86, 1-25, 10.1103/physrevd.86.074007.
- Katherine J. Mack; Robert McNees; Bounds on extra dimensions from micro black holes in the context of the metastable Higgs vacuum. Marcelo Gleiser; Metastability in the early Universe. Physical Review D 20 199, 99, 063001, 10.1103/physrevd.99.063001.0, 42, 3350-3361, 10.1103/physrevd.42.3350.
- Itzhak Bars; Paul J. Steinhardt; Neil Turok; Cyclic cosmology, conformal symmetry and the metastability of the Higgs. Katherine J. Mack; Robert McNees; Bounds on extra dimensions from micro black holes in the context of the metastable Higgs vacuum. Physicsal Letters B Review D 2013, 726, 50-55, 10.1016/j.physletb.2013.08.071.9, 99, 063001, 10.1103/physrevd.99.063001.
- Nikolaos Tetradis; Black holes and Higgs stability. Journal of Cosmology and Astroparticle Itzhak Bars; Paul J. Steinhardt; Neil Turok; Cyclic cosmology, conformal symmetry and the metastability of the Higgs. Physics Letters B 2016, 3, 72016, 036-036, 10.1088/1475-7516/2016/09/036., 50-55, 10.1016/j.physletb.2013.08.071.
- J A Santiago; G Chacón-Acosta; O González-Gaxiola; Effective potentials in geodesic curves on surfaces. Nikolaos Tetradis; Black holes and Higgs stability. Journal of PhCosmologysics: Conference Serie and Astroparticle Physics 2014, 545, 012014, 10.1088/1742-6596/545/1/012014.6, 2016, 036-036, 10.1088/1475-7516/2016/09/036.
- Bernhard Haisch; Alfonson Rueda; H.E. Puthoff; Physics of the zero-point field: implications for inertia, gravitation and mass. SpecJ A Santiago; G Chacón-Acosta; O González-Gaxiola; Effective potentials in geodesic curves on surfaces. Journalations in Science and Technology of Physics: Conference Series 201997, 20, 99-114, 10.1023/a:1018516704228.4, 545, 012014, 10.1088/1742-6596/545/1/012014.
- Bo Song; Shovan Dutta; Shaurya Bhave; Jr-Chiun Yu; Edward Carter; Nigel Cooper; Ulrich Schneider; Realizing discontinuous quantum phase transitions in a strongly correlated driven optical lattice. NBernhard Haisch; Alfonson Rueda; H.E. Puthoff; Physics of the zero-point field: implications for inertia, gravitation and mass. Speculaturions in Science Phand Technologysics 2022, 18, 259-264, 10.1038/s41567-021-01476-w. 1997, 20, 99-114, 10.1023/a:1018516704228.
- Are We on the Brink of the Higgs Abyss? . Physcis. Retrieved 2022-7-31Bo Song; Shovan Dutta; Shaurya Bhave; Jr-Chiun Yu; Edward Carter; Nigel Cooper; Ulrich Schneider; Realizing discontinuous quantum phase transitions in a strongly correlated driven optical lattice. Nature Physics 2022, 18, 259-264, 10.1038/s41567-021-01476-w.
- E.M Henley; High energy diffractive dissociation of pions and the A1. Annals of Physics 1971, 63, 541-548, 10.1016/0003-4916(71)90027-3.Are We on the Brink of the Higgs Abyss? . Physcis. Retrieved 2022-7-31
- Krishnanand Sinha; On the oscillator strength and the dissociation energy of CN molecules. ReE.M Henley; High energy diffractive dissociation of pions and the A1. Annals of PhysearichGate s 1986, 1, 1-6.71, 63, 541-548, 10.1016/0003-4916(71)90027-3.
- J. Hussels; N. Hölsch; C.-F. Cheng; E. J. Salumbides; H. L. Bethlem; K. S. E. Eikema; Ch. Jungen; M. Beyer; F. Merkt; W. Ubachs; et al. Improved ionization and dissociation energies of the deuterium molecule. PhyKrishnanand Sinha; On the oscillator strength and the dissociation energy of CN molecules. Resiearcal RhGateview A 2022, 1986, 105, 022820, 10.1103/physreva.105.022820., 1-6.
- C. H. L. Goodman; Ionic-Covalent Bonding in Crystals. NJ. Hussels; N. Hölsch; C.-F. Cheng; E. J. Salumbides; H. L. Bethlem; K. S. E. Eikema; Ch. Jungen; M. Beyer; F. Merkt; W. Ubachs; et al. Improved ionization and dissociation energies of the deuterium molecule. Physicaturl Revie 196w A 20, 22, 187, 590-591, 10.1038/187590a0.05, 022820, 10.1103/physreva.105.022820.
- John Bannister Goodenough; First-order changes in ionic/covalent bonding. FerC. H. L. Goodman; Ionic-Covalent Bonding in Crystals. Naturoelectrics 1992, 60, 130, 77-86, 10.1080/00150199208019535.87, 590-591, 10.1038/187590a0.
- E.V. Kolontsova; Å.â. Êîëîíöîâà; Radiation-induced states in crystals with ionic-covalent bonds. UspJohn Bannister Goodenough; First-order changes in ionic/covalent bonding. Ferroelekhctri Fizichecskih Nauk 19987, 2, 151, 149-172, 10.3367/ufnr.0151.198701g.0149.30, 77-86, 10.1080/00150199208019535.
- Weizhang Huang; Weishi Liu; Yufei Yu; Permanent charge effects on ionic flow: a numerical study of flux ratios and their bifurcation. E.V. Kolontsova; Å.â. Êîëîíöîâà; Radiation-induced states in crystals with ionic-covalent bonds. Uspekhi Fizicheskih NarXiv 2020, uk 1987, 151, 1-31, 10.48550/arXiv.2003.11223., 149-172, 10.3367/ufnr.0151.198701g.0149.
- Giulia L. Celora; Matthew G. Hennessy; Andreas Münch; Barbara Wagner; Sarah L. Waters; The dynamics of a collapsing polyelectrolyte gel. null Weizhang Huang; Weishi Liu; Yufei Yu; Permanent charge effects on ionic flow: a numerical study of flux ratios and their bifurcation. arXiv 2021, 0, 1, 1-34, 10.48550/arXiv.2105.06495., 1-31, 10.48550/arXiv.2003.11223.
- M. B. Fröb; C. Rein; R. Verch; Graviton corrections to the Newtonian potential using invariant observables. JoGiulia L. Celora; Matthew G. Hennessy; Andreas Münch; Barbara Wagner; Sarah L. Waters; The dynamics of a collapsing polyelectrolyte gel. nurnall of High Energy Physics 2022, 2022, 1-29, 10.1007/jhep01(2022)180.1, 1, 1-34, 10.48550/arXiv.2105.06495.
- Lintao Tan; Nikolaos Christos Tsamis; Richard Paul Woodard; How Inflationary Gravitons Affect the Force of Gravity. UM. B. Fröb; C. Rein; R. Verch; Graviton corrections to the Newtonian potential using invariant observables. Journal of Hiverse gh Energy Physics 2022, 8, 376, 10.3390/universe8070376., 2022, 1-29, 10.1007/jhep01(2022)180.
- Mark Kowitt; Gravitational repulsion and Dirac antimatter. ILintao Tan; Nikolaos Christos Tsamis; Richard Paul Woodard; How Inflationary Gravitons Affect the Force of Gravity. Unternational Journal of Theorversetical Physics 1996, 35, 605-631, 10.1007/bf02082828. 2022, 8, 376, 10.3390/universe8070376.
- Tong Bor Tang; Li Zhi Fang; The cosmic asymmetry in matter-antimatter. VisMark Kowitt; Gravitational repulsion and Dirac antimatter. Internas in Astronomtional Journal of Theoretical Phy sics 19984, 27, 1-23, 10.1016/0083-6656(84)90010-2.6, 35, 605-631, 10.1007/bf02082828.
- Anonymous; Universe Preceded by an Antiuniverse?. PhyTong Bor Tang; Li Zhi Fang; The cosmic asymmetry in matter-antimatter. Vistas icn As 20tronomy 198, 11, 1, 10.1103/physics.11.s147.4, 27, 1-23, 10.1016/0083-6656(84)90010-2.
- S.J. Robles-Pérez; Quantum Creation of a Universe–Antiuniverse Pair. Acta Anonymous; Universe Preceded by an Antiuniverse?. Physica Polonica B Proceedings Supplement 2020, 18, 113, 1-7, 10.5506/aphyspolbsupp.13.325., 1, 10.1103/physics.11.s147.
- R. L. Jaffe; Casimir effect and the quantum vacuum. S.J. Robles-Pérez; Quantum Creation of a Universe–Antiuniverse Pair. Acta Physica Pol Review D onica B Proceedings Supplement 20205, 72, 021301, 10.1103/physrevd.72.021301., 13, 1-7, 10.5506/aphyspolbsupp.13.325.
- Gilles Cohen-Tannoudji; The de Broglie universal substratum, the Lochak monopoles and the dark universe. R. L. Jaffe; Casimir effect and the quantum vacuum. PhysicarXl Reviv ew D 20105, 1, 1-20, 10.48550/arXiv.1507.00460., 72, 021301, 10.1103/physrevd.72.021301.
- Four reasons why the quantum vacuum may explain dark matter . PhysOrg.com. Retrieved 2022-7-28Gilles Cohen-Tannoudji; The de Broglie universal substratum, the Lochak monopoles and the dark universe. arXiv 2015, 1, 1-20, 10.48550/arXiv.1507.00460.
- Antonio Capolupo; Quantum Vacuum, Dark Matter, Dark Energy, and Spontaneous Supersymmetry Breaking. Advances in High Energy Physics 2018, 2018, 1-7, 10.1155/2018/9840351.Four reasons why the quantum vacuum may explain dark matter . PhysOrg.com. Retrieved 2022-7-28
- Dragan Slavkov Hajdukovic; Quantum vacuum and dark matter. Antonio Capolupo; Quantum Vacuum, Dark Matter, Dark Energy, and Spontaneous Supersymmetry Breaking. Astrophysidvancs and Space Science es in High Energy Physics 2011, 337, 9-14, 10.1007/s10509-011-0938-9.8, 2018, 1-7, 10.1155/2018/9840351.
- Davide Castelvecchi; New type of dark energy could solve Universe expansion mystery. NaDragan Slavkov Hajdukovic; Quantum vacuum and dark matter. Asturophysics and Space Science 20211, 1, 1, 10.1038/d41586-021-02531-5., 337, 9-14, 10.1007/s10509-011-0938-9.
- Simeon Bird; Andrea Albert; Will Dawson; Yacine Ali-Haimoud; Adam Coogan; Alex Drlica-Wagner; Qi Feng; Derek Inman; Keisuke Inomata; Ely Kovetz; et al.Alexander KusenkoBenjamin V. LehmannJulian B. MunozRajeev SinghVolodymyr TakhistovYu-Dai Tsai Snowmass2021 Cosmic Frontier White Paper:Primordial Black Hole Dark Matter. Davide Castelvecchi; New type of dark energy could solve Universe expansion mystery. NaturXiv e 2022, 1, 1, 1-22, 10.48550/arXiv.2203.08967., 1, 10.1038/d41586-021-02531-5.
- Eric V. Linder; Dark Energy, Expansion History of the Universe, and SNAP. PROCEEDINGS OF THE INTERNATIONAL CONFERENCE “PHYSICAL MESOMECHANICS. MATERIALS WITH MULTILEVEL HIERARCHICAL STRUCTURE AND INTELLIGENT MANUFACTURING TECHNOLOGY” Simeon Bird; Andrea Albert; Will Dawson; Yacine Ali-Haimoud; Adam Coogan; Alex Drlica-Wagner; Qi Feng; Derek Inman; Keisuke Inomata; Ely Kovetz; et al.Alexander KusenkoBenjamin V. LehmannJulian B. MunozRajeev SinghVolodymyr TakhistovYu-Dai Tsai Snowmass2021 Cosmic Frontier White Paper:Primordial Black Hole Dark Matter. arXiv 2003, 655, 193-207, 10.1063/1.1543500.22, 1, 1-22, 10.48550/arXiv.2203.08967.
- Jacob Schaf; dark energy expansion. Eric V. Linder; Dark Energy, Expansion History of the Universe, and SNAP. PROCEEDINGS OF THE INTERNATIONAL CONFERENCE “PHYSICAL MESOMECHANICS. MATERIALS WITH MUniversalLTILEVEL Journal of Physics and Application HIERARCHICAL STRUCTURE AND INTELLIGENT MANUFACTURING TECHNOLOGY” 20015, 9, 182-187, 10.13189/ujpa.2015.090403.3, 655, 193-207, 10.1063/1.1543500.
- Dragan Huterer; David Kirkby; Rachel Bean; Andrew Connolly; Kyle Dawson; Scott Dodelson; August Evrard; Bhuvnesh Jain; Michael Jarvis; Eric Linder; et al.Rachel MandelbaumMorgan MayAlvise RaccanelliBeth ReidEduardo RozoFabian SchmidtNeelima SehgalAnže SlosarAlex van EngelenHao-Yi WuGongbo Zhao Growth of cosmic structure: Probing dark energy beyond expansion. AJacob Schaf; dark energy expansion. Universtal Jouroparticlenal of Physics and Application 2014, 63, 23-41, 10.1016/j.astropartphys.2014.07.004.5, 9, 182-187, 10.13189/ujpa.2015.090403.
- Gang Xin; Peng Wang; Exploring superposition state in multi-scale quantum harmonic oscillator algorithm. Dragan Huterer; David Kirkby; Rachel Bean; Andrew Connolly; Kyle Dawson; Scott Dodelson; August Evrard; Bhuvnesh Jain; Michael Jarvis; Eric Linder; et al.Rachel MandelbaumMorgan MayAlvise RaccanelliBeth ReidEduardo RozoFabian SchmidtNeelima SehgalAnže SlosarAlex van EngelenHao-Yi WuGongbo Zhao Growth of cosmic structure: Probing dark energy beyond expansion. Astropplied Soft Computing article Physics 2021, 107, 107398, 10.1016/j.asoc.2021.107398.4, 63, 23-41, 10.1016/j.astropartphys.2014.07.004.
- Eva Zakka-Bajjani; François Nguyen; Minhyea Lee; Leila R. Vale; Raymond W. Simmonds; Jose Aumentado; Quantum superposition of a single microwave photon in two different ’colour’ states. NaGang Xin; Peng Wang; Exploring superposition state in multi-scale quantum harmonic oscillator algorithm. Applied Soft Compure Physics ting 20211, , 107, 599-603, 10.1038/nphys2035., 107398, 10.1016/j.asoc.2021.107398.
- Martin J. Renner; Časlav Brukner; Computational Advantage from a Quantum Superposition of Qubit Gate Orders. Eva Zakka-Bajjani; François Nguyen; Minhyea Lee; Leila R. Vale; Raymond W. Simmonds; Jose Aumentado; Quantum superposition of a single microwave photon in two different ’colour’ states. Nature Physical Review Letters 2022, 128, 230503, 10.1103/physrevlett.128.230503.11, 7, 599-603, 10.1038/nphys2035.
- P. A. Cook; Meson coupling constants in a quark model. IMartin J. Renner; Časlav Brukner; Computational Advantage from a Quantum Superposition of Qubit Gate Orders. Physical NuoRevo Cimento A Serieiew Letters 2022, 10 1967, 428, 570-572, 10.1007/bf02818032., 230503, 10.1103/physrevlett.128.230503.
- Fujio Takagi; Meson-Baryon Coupling Constants in the Quark Model. PrP. A. Cook; Meson coupling constants in a quark model. Il Nuovogr Cimess of Theoretical Physics nto A Series 10 1967, 37, 1047-1048, 10.1143/ptp.37.1047., 48, 570-572, 10.1007/bf02818032.
- E. M. Henley; T. Oka; J. D. Vergados; Meson-nucleon coupling constants in a quark model. FFujio Takagi; Meson-Baryon Coupling Constants in the Quark Model. Progress of Thew-Body Systemretical Physics 1990, 9, 75-87, 10.1007/bf01091699.67, 37, 1047-1048, 10.1143/ptp.37.1047.
- R. Brout; From asymptotic freedom to quark confinement. NuclE. M. Henley; T. Oka; J. D. Vergados; Meson-nucleon coupling constants in a quark model. Fearw-Body PhysicSystems B 1988, 310, 127-140, 10.1016/0550-3213(88)90057-0.90, 9, 75-87, 10.1007/bf01091699.
- Kei-Ichi Kondo; Abelian-Projected Effective Gauge Theory of QCD with Asymptotic Freedom and Quark Confinement. ProgrR. Brout; From asymptotic freedom to quark confinement. Nucless of Theoaretical Physics Supplement B 19988, 1, 31, 243-255, 10.1143/ptps.131.243.0, 127-140, 10.1016/0550-3213(88)90057-0.
- Kanako Yamazaki; T. Matsui; Gordon Baym; Entropy in the quark–hadron transition. NuKei-Ichi Kondo; Abelian-Projected Effective Gauge Theory of QCD with Asymptotic Freedom and Quark Confinement. Progress of Theoreticalear Physics A 20Supplement 15, 9998, 133, 245-255, 10.1016/j.nuclphysa.2014.10.046.1, 243-255, 10.1143/ptps.131.243.
- David Dudal; Subhash Mahapatra; Thermal entropy of a quark-antiquark pair above and below deconfinement from a dynamical holographic QCD model. Kanako Yamazaki; T. Matsui; Gordon Baym; Entropy in the quark–hadron transition. Nuclear Physicals Review D A 2017, 5, 96, 126010, 10.1103/physrevd.96.126010.33, 245-255, 10.1016/j.nuclphysa.2014.10.046.
- Tri Quoc Truong; Tadashi Tsubone; Munehisa Sekikawa; Naohiko Inaba; Border-collision bifurcations and Arnol’d tongues in two coupled piecewise-constant oscillators. David Dudal; Subhash Mahapatra; Thermal entropy of a quark-antiquark pair above and below deconfinement from a dynamical holographic QCD model. Physical D: Nonlinear Phenomena Review D 2019, 401, 132148, 10.1016/j.physd.2019.132148.7, 96, 126010, 10.1103/physrevd.96.126010.
- D Gabor; Plasma oscillations. BrTri Quoc Truong; Tadashi Tsubone; Munehisa Sekikawa; Naohiko Inaba; Border-collision bifurcations and Arnol’d tongues in two coupled piecewise-constant oscillators. Physitishca D: Journal of Applied Physics Nonlinear Phenomena 201951, 2, 209-218, 10.1088/0508-3443/2/8/301., 401, 132148, 10.1016/j.physd.2019.132148.
- Toshio Nakayama; Irreversibility in Plasmas: Entropy Production. PD Gabor; Plasma oscillations. British Jogress of Theoreticalurnal of Applied Physics 1974, 51, 77-81, 10.1143/ptp.51.77.51, 2, 209-218, 10.1088/0508-3443/2/8/301.
- Ettore Minardi; Minardi, E. Thermodynamics of High Temperature Plasmas. Entropy, 2009, 11, 124-221. EntToshio Nakayama; Irreversibility in Plasmas: Entropy Production. Progress opf Theoretical Phy 200sics 19, 74, 511, 457-462, 10.3390/e11030457., 77-81, 10.1143/ptp.51.77.
- R. Shankar; Determination of the quark-gluon coupling constant. PhEttore Minardi; Minardi, E. Thermodynamics of High Temperature Plasmas. Entropy, 2009, 11, 124-221. Entropysical Review D 1 200977, , 115, 755-758, 10.1103/physrevd.15.755., 457-462, 10.3390/e11030457.
- M. A. Braun; Reggeized gluons with a running coupling constant. R. Shankar; Determination of the quark-gluon coupling constant. Physicsal Letters B Review D 1995, 348, 190-195, 10.1016/0370-2693(95)00101-p.77, 15, 755-758, 10.1103/physrevd.15.755.
- M. Althoff; W. Braunschweig; F.J. Kirschfink; K. Lübelsmeyer; H.-U. Martyn; J. Rimkus; P. Rosskamp; H.G. Sander; D. Schmitz; H. Siebke; et al.W. WallraffH.M. FischerH. HartmannA. JockschG. KnopL. KöpkeH. KolanoskiH. KückV. MertensR. WedemeyerM. WollstadtY. EisenbergA. EskreysK. GatherH. HultschigP. JoosU. KötzH. KowalskiA. LadageB. LöhrD. LükeP. MättigD. NotzR.J. NowakJ. PyrlikM. RushtonW. SchütteD. TrinesG. WolfCh. XiaoR. FohrmannE. HilgerT. KrachtH.L. KrasemannP. LeuE. LohrmannD. PandoulasG. PoelzK.U. PösneckerB.H. WiikR. BeuselinckD.M. BinnieA.J. CampbellP. DornanB. FosterD.A. GarbuttC. JenkinsT.D. JonesW.G. JonesJ. McCardleJ.K. SedgbeerJ. ThomasW.A.T. Wan AbdullahK.W. BellM.G. BowlerP. BullR.J. CashmoreP.E.L. ClarkeR. DevenishP. GrossmannC.M. HawkesS.L. LloydG.L. SalmonT.R. WyattC. YoungmanG.E. FordenJ.C. HartJ. HarveyD.K. HasellJ. ProudfootD.H. SaxonF. BarreiroM. DittmarM. HolderG. KreutzB. NeumannE. DuchovniU. KarshonG. MikenbergR. MirD. RevelE. RonatA. ShapiraG. YekutieliG. BarankoT. BarklowA. CaldwellM. CherneyJ.M. IzenM. MermikidesG. RudolphD. StromM. TakashimaH. VenkataramaniaE. WicklundSau Lan WuG. ZobernigTASSO Collaboration Experimental test of the flavor independence of the quark-gluon coupling constant. M. A. Braun; Reggeized gluons with a running coupling constant. Physics Letters B 19984, 15, 348, 317-324, 10.1016/0370-2693(84)91668-x., 190-195, 10.1016/0370-2693(95)00101-p.
- Lawrence Slifkin; Entropy and the Frequency of a Harmonic Oscillator. American Journal of M. Althoff; W. Braunschweig; F.J. Kirschfink; K. Lübelsmeyer; H.-U. Martyn; J. Rimkus; P. Rosskamp; H.G. Sander; D. Schmitz; H. Siebke; et al.W. WallraffH.M. FischerH. HartmannA. JockschG. KnopL. KöpkeH. KolanoskiH. KückV. MertensR. WedemeyerM. WollstadtY. EisenbergA. EskreysK. GatherH. HultschigP. JoosU. KötzH. KowalskiA. LadageB. LöhrD. LükeP. MättigD. NotzR.J. NowakJ. PyrlikM. RushtonW. SchütteD. TrinesG. WolfCh. XiaoR. FohrmannE. HilgerT. KrachtH.L. KrasemannP. LeuE. LohrmannD. PandoulasG. PoelzK.U. PösneckerB.H. WiikR. BeuselinckD.M. BinnieA.J. CampbellP. DornanB. FosterD.A. GarbuttC. JenkinsT.D. JonesW.G. JonesJ. McCardleJ.K. SedgbeerJ. ThomasW.A.T. Wan AbdullahK.W. BellM.G. BowlerP. BullR.J. CashmoreP.E.L. ClarkeR. DevenishP. GrossmannC.M. HawkesS.L. LloydG.L. SalmonT.R. WyattC. YoungmanG.E. FordenJ.C. HartJ. HarveyD.K. HasellJ. ProudfootD.H. SaxonF. BarreiroM. DittmarM. HolderG. KreutzB. NeumannE. DuchovniU. KarshonG. MikenbergR. MirD. RevelE. RonatA. ShapiraG. YekutieliG. BarankoT. BarklowA. CaldwellM. CherneyJ.M. IzenM. MermikidesG. RudolphD. StromM. TakashimaH. VenkataramaniaE. WicklundSau Lan WuG. ZobernigTASSO Collaboration Experimental test of the flavor independence of the quark-gluon coupling constant. Physics Letters B 1965, 84, 133, 408-408, 10.1119/1.1971569.8, 317-324, 10.1016/0370-2693(84)91668-x.
- N. Fornengo; C. Giunti; C.W. Kim; J. Song; Gravitational effects on the neutrino oscillation in vacuum. NuLawrence Slifkin; Entropy and the Frequency of a Harmonic Oscillator. Americlear n Journal of Physics B - Proceedings Supplements 1999, 70, 264-266, 10.1016/s0920-5632(98)00435-6.65, 33, 408-408, 10.1119/1.1971569.
- Quantum Field and 2nd Quantization (2021 Edition) . universe-review.ca. Retrieved 2022-7-29N. Fornengo; C. Giunti; C.W. Kim; J. Song; Gravitational effects on the neutrino oscillation in vacuum. Nuclear Physics B - Proceedings Supplements 1999, 70, 264-266, 10.1016/s0920-5632(98)00435-6.
- Anharmonic Oscillator . GitHub. Retrieved 2022-8-2 Quantum Field and 2nd Quantization (2021 Edition) . universe-review.ca. Retrieved 2022-7-29
- Damiano Anselmi; Purely Virtual Particles in Quantum Gravity, Inflationary Cosmology and Collider Physics. Symmetry 2022, 14, 521, 10.3390/sym14030521.Anharmonic Oscillator . GitHub. Retrieved 2022-8-2
- Janne Mikael Karimäki; Virtual Particle Interpretation of Quantum Mechanics - a non-dualistic model of QM with a natural probability interpretation. aDamiano Anselmi; Purely Virtual Particles in Quantum Gravity, Inflationary Cosmology and Collider Physics. SymmetrXiv y 20122, 1, 1-8, 10.48550/arXiv.1206.1237.4, 521, 10.3390/sym14030521.
- Janne Mikael Karimäki; Virtual Particle Interpretation of Quantum Mechanics - a non-dualistic model of QM with a natural probability interpretation. arXiv 2012, 1, 1-8, 10.48550/arXiv.1206.1237.
