The functioning of our universe and atomic is based on the oscillation of the particle itself and asymmetrically between matter and antimatter. This mechanism is a classical an-harmonic oscillator and uses a linear oscillation of the particle, where the energy can be represented by the graph of a potential well followed by the principle of energy conservation between kinetic energy and potential energy. This an-harmonic oscillation therefore occurs with an gravitational oscillator (see "hole through the earth simple harmonic motion"), followed by an singularity avoidance. Indeed the important kinetics of the particle leads to an singularity avoidance over the supermassive black hole to plot the Higgs field.
- anharmonic oscillator
- singularity avoidance
- gravitational oscillator
- cyclic model
- oscillating Universe
- oscillating model
- Higgs
- universe
- theory
- kartazion
1. Introduction
The theory and the thought experiment of this paper followed by the observations and calculations already acquired, can lead us to the following reasoning.
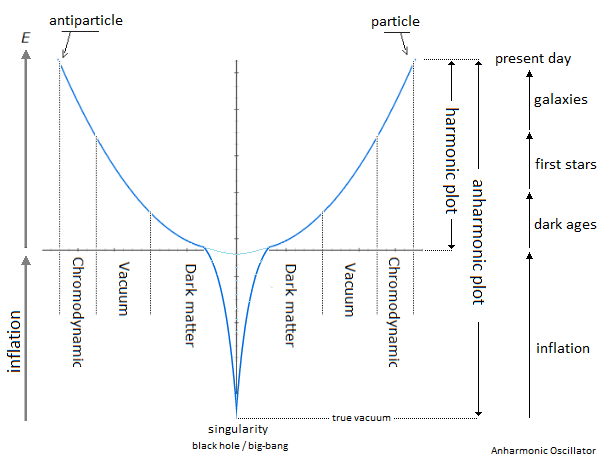
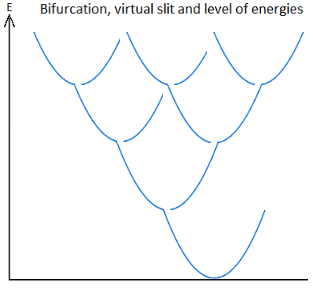
Figure 1. Once Upon a Time the Universe: Anharmonic Oscillator.
The functioning of our universe and atomic is based on the oscillation of the particle itself [1][2][3]. This mechanism is a classical an-harmonic oscillator and uses a linear oscillation of the particle, where the energy can be represented by the graph of a potential well between Kinetic Energy and Potential Energy through an gravitationnal oscillator. This an-harmonic oscillation of there particle therefore occurs between matter and antimatter [4][5], followed by an avoidance of the gravitational singularity. This singularity avoidance [6][7][8] is of the supermassive black hole and/or big-bang type and is due to the high kinetics of the particle. On the other hand, and at total rest, this particle by is at tts energy representation, is at the bottom of the well of potential well, inl, at the lowest level, at the singularity, namely the total collapse of the universe which represents athe state of true vacuum. But again and by a , and through more sustained oscillation, a singularity avoidance occurs in opposite ofcontrast to the rest, and creates the levitation of the particle in's energy to higher energy levels in its potential well. This singularity avoidance allows access to the current vacuum and is due through to to the high Kkinetics and/or inertia of the particle. The role of the singularity in our model is fundamental and implies that it is the source and driver of the actual known result of quantum and cosmological fluctuations in relation to the motion of the particle.
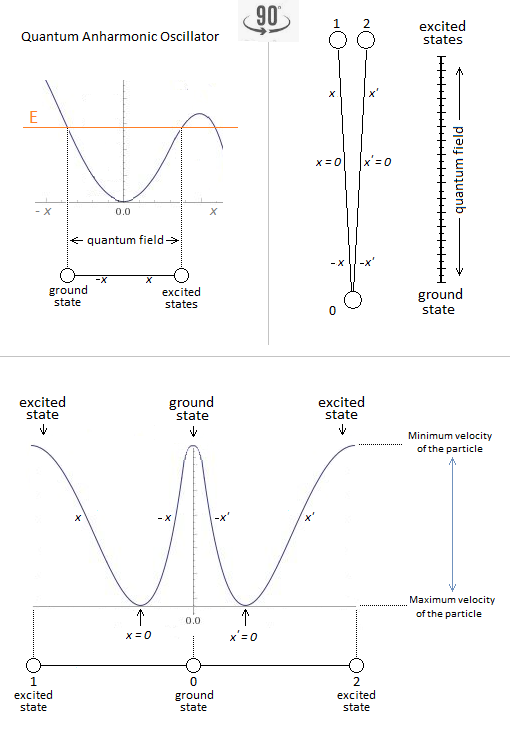
Harmonic Oscillator vs Anharmonic Oscillator. Indeed the difference is made here and is between the ideal harmonic layout and the absolut anharmonic layout of the energy captured in potential well. In the case of singularity avoidance due to the high Kinetic Energy of the particle, the plot of the curve of the potential well tends towards a harmonic shape rather than an anharmonic one. Moreover the anharmonic implication can be double: the variation of speed of the particle followed by the shape of the potential well due to the singularity involves this anharmonicity. More exhaustively we can still imply the internuclear distance and the morse potentials to give an another characteristic of anharmonicity to the oscillator.
In the following illustration Figure 2, Figure 3 an integration of the gravitational singularity disturbs the harmonic shape of the potential well. The greater the kinetics of the particle in its oscillation, the more the shape of the potential well tends towards harmony by avoidance of gravitational singularity. But if the kinetics of the particle isare stopped, then the particle falls at the bottom of this gravitational singularity and traces the anharmonicity of the potential well.
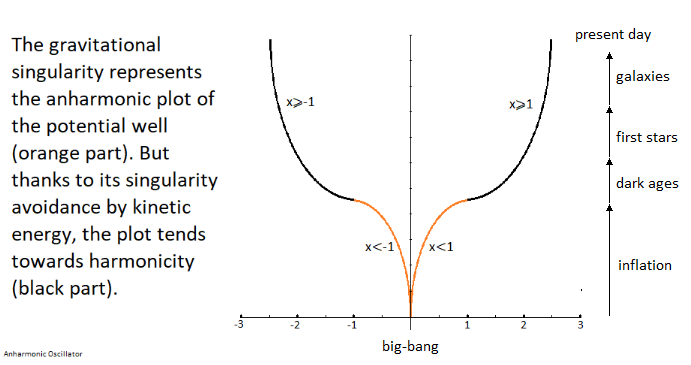
Figure 2. Singularity avoidance by kinetics and harmonicity, and anharmonicity.
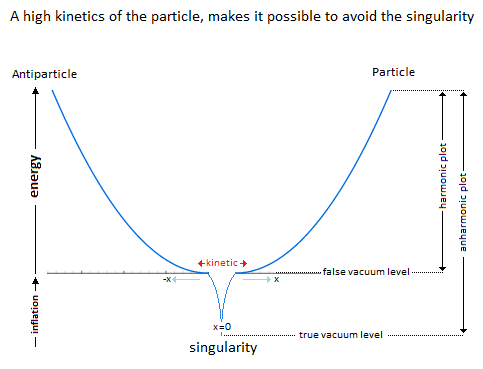
In a second part of this introduction, it is a question of the singularity avoidance where the particle through its potential energy path, traces the Higgs field. This Potential Energy is in relation to the depth of the gravitationnal singularity, because to pass over a black hole would have for value an enormous Potential Energy, and would trace the curve of the potential of Higgs (Figure 4).
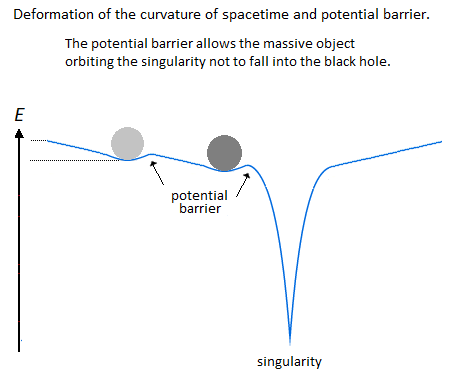
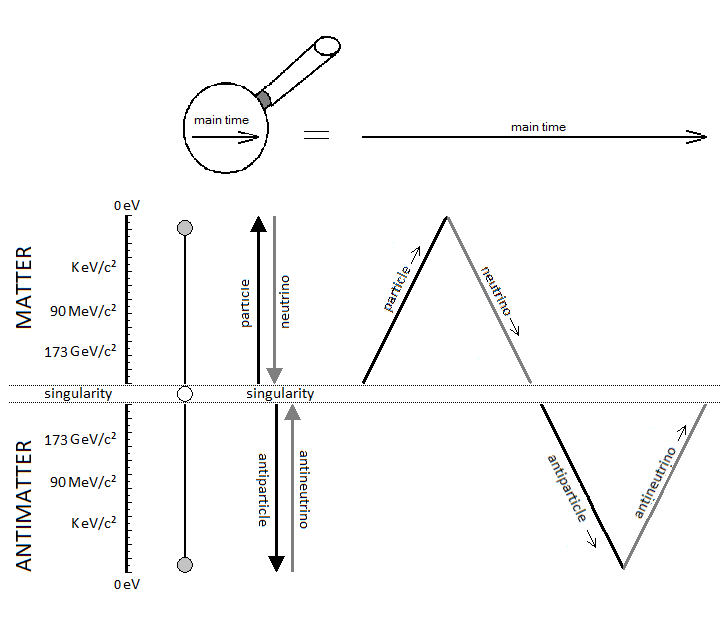
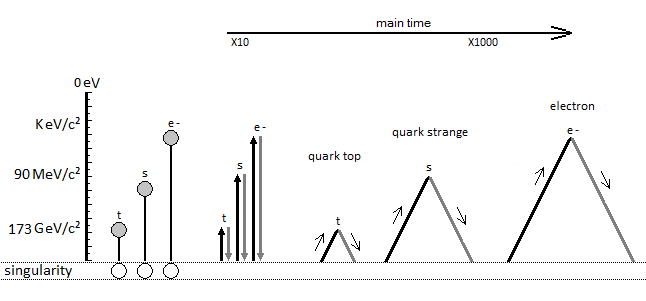
In a second part of this introduction, it is question of the singularity avoidance where the particle by its path of Potential Energy, traces the Higgs field. This Potential Energy is related to the depth of the gravitational singularity, because to pass over a black hole would have for value an enormous Potential Energy, and would trace the curve of the Higgs potential. Perpetual motion is utopian. But in our case it represents an oscillation without mechanical constraint followed by the principle and the law of conservation of energy. In an interpretation of classical mechanics, the an-harmonic oscillation of the particle can be represented through a gravitational oscillator (Figure 54). It is initially used gravity to subject by attraction a movement to the particle. Here is the example chosen of an oscillation of the particle which uses the same direction as the vector of gravity. The acquisition of kinetic energy through potential energy in vacuum condition allows endless continuity of motion. Its description is based on the "Hole Through the Earth Example" [9][10] which does not really have an example in French but which is nevertheless well studied for its principle. Here we have an summary explanation: "If you drilled a hole in the axis of the Earth from pole to pole, and inserted a long, thin vacuum chamber into it, and then dropped an object into one end of that chamber, it would fall into the hole, picking up speed and it would move very fast when it reached the center of the Earth so it would continue until it reached the other pole where it would stop, then fall back "bounce" to come back and start again perpetually." (Search engine and keywords 'hole through the earth simple harmonic motion'). This linear gravitational oscillator in Figure 54 uses a particle of mass m oscillating vertically along the gravity vector G. The oscillation has two phases. The first is the falling phase of the particle with its Potential Energy PE and the second is the reverse phase which corresponds to the Kinetic Energy KE. It is from the center of the Earth that which is in Potential Energy is transformed into Kinetic Energy and is reversed at the level at the point of origine 0 or x=0. In the following illustration in Figure 65, the integration of the gravitationnal singularity is not yet represented. If the energy potential well in Figure 65 has a curved shape, it represents the form of the amount of energy delivered to the particle according to x. Which does not mean that the particle moves in a half-moon. The particle moves nice and well in a straight line in a radiative and linear way. In the Figure 65 we can distinguish three types of possible interpretations of states or/and energy paths due to displacement of the particle. In 1 and at the bottom of the harmonic potential well at x=0, we have the rest of the motionless particle or the ZPE (the lowest possible energy in a quantum system [11][12]). In 2 and with the Kinetic Energy applied to the particle, is at x=0 the maximum speed of the particle and drawing an energy path in a form of harmonic curve. In 3 it should be noted that the ideal trajectory of the energy path is the short circuit type between matter and antimatter and would trace a straight line, namely the shortest energy path in the potential well. This utopian energy path is actually not the conventional form of energy delivered to the particle. However, the annihilation of the electron/positron pair into a gamma photon should indicate this short-circuit type trajectory, and finally defined the characteristic of a boson. In conclusion, for the gravitational oscillator presented in Figure 54, use the distribution of the two energies follows the following Figure 76 and operates according to the linear displacement of the particle, i.e. the alternation of the Potential Energy PE with the Kinetic Energy KE [12][13][14][15][16][17][18]. Potential Energy - Kinetic Energy = 0 In our model the source [1819] and the material existence as we know it, is based on the implication of the singularity of the big-bang type for the universe [1920][2021] and of the supermassive black hole type for the functioning for the galaxies [21][22][23][24], and other theoretical singularity as like that of the center of an atom [2425]. In other words, the divergent evolution of the volume of the singularity is responsible for the presence of the matter that remains in its space-time. As gravity (Potential Energy) pulls the particle towards the core of the singularity, and who approaches it to fall inside, is then suddenly expelled by pure energy emanating from that same singularity [25][26][27][28]. Indeed the singularity generates in 1 the gravitational attraction noted Potential Energy PE. The acquisition of the Kinetic Energy to the particle is accumulates through the movement due to the Potential Energy, and a potential energy barrier allow to deflect the particle out of the singularity. The emanation of this energy complementary to the total Kinetic Energy is in 2 the source of energy by scratching and/or astrophysical relativistic jet or Hawking radiation emanates from this same singularity and to make an avoidance of it. Moreover in 3 it should be noted that the singularity generates eletric charges on the particle. In a more speculative and exotic definition and given our knowledge of the singularity in terms of gravitation followed by its ratio of time dilation, we could associate the center of the earth as such. Indeed for the particle which oscillates in the radiative oscillation from the center to the surface and vice versa, it becomes easy to imagine an gravitationnal singularity at the level of the Earth's core in the same way as the supermassive black hole in relation to its galaxy [2829][2930]. Singularity avoidance [6][7][8] is due to the high Kinetic Energy of the particle. At x=0 when the particle is going as fast as possible, its Kinetic Energy allows it not to fall at the bottom of the well at the level of the gravitational singularity. Gravity (Potential Energy) corresponds to the matter attracted towards this singularity, while energy pushes it back with the Kinetic Energy accumulating through Potential Energy and can also be increased by additional energy due to the emanation of this same singularity [2526][2627]. In our case it is simply a particle rather than a cluster of matter. A significant kinetics of the particle makes it possible to avoid the singularity, and the path takes above this singularity by the particle determines the plot of the Higgs field (vector). Another example of singularity avoidance with the Higgs implication (scalar field) [3031]. In a second time the theoretical junction between the singularity avoidance and the Higgs field can be done by the enormous Potential Energy. Indeed, the Potential Energy being that in relation to the depth of the gravitational singularity gives the particle a much greater mass, or even a maximum value. The Higgs field and potential are also well used to be able to represent the metastability [31][32][33][34] of the universe, as well as its interpretation as a quantum particle for its origin of the mass. Singularity avoidance = enormous Potential Energy = Higgs mechanism = mass link We indicate a Potential Energy barrier around gravitational singularities [3435]. This barrier is due to the deformation of the space-time curvature. At least a difference in level where the Potential Energy is felt around the mass object. Without Kinetic Energy, the inertia of the object (or particle) allows it to slide along the potential barrier that defines the path of the orbit around an even more massive object. In other words, the deformation of the space-time curvature due to an average object is felt at the level of the heights of the energies, and creates a barrier (Figure 120). The ZPE [12] (Zero Point Energy) represents the initial perturbation of the particle. At the quantum level this means that when the particle is at rest at the bottom of the harmonic potential well, the particle undergoes an oscillating disturbance. In cosmology this disturbance represents the inertial movement as an object orbiting around the gravitational singularity/massive object. In other words, the initial quantum disturbance of the Zero Point Energy (ZPE) corresponds to the cosmological movement of the object/particle located in the false vacuum in orbit around the gravitational singularity [3536]. Deformation also occurs for massive objects like stars. It should be understood that in the event of a attempt to stop followed by slowing down of the kinetics of the particle due to the high potential barrier, the particle will then tend to pass through by the tunnel effect, instead of the singularity avoidance by the Higgs field and finds itself at the level of the black hole horizon event. This being said, this does not mean that the particle will finally reach true vacuum because the minimum kinetic/inertia was then send to the particle in order to be able to take the contuinity of its journey throug the event horizon. This contrary scenario of the Kinetic Energy sent or subjected to the particle in order to be able to eject it again into the upper harmonic well of our universe/galaxies, represent the singularity avoidance by Higgs mecanism toward the upper harmonic energy well of our universe/galaxies. This second Interpretation is to be considered as a singularity avoidance at the horizon event of a black hole (Figure 11) instead of the singularity avoidance over it by the Higgs field. Figure 11. Singularity avoidance at the horizon event of a black hole by quantum tunneling and Hawking radiation. Vacuum metastability is determined by the amount of Kinetic Energy applied to the particle to trace its potential field. If the Kinetic Energy of the particle is sufficient and therefore if the range of the energy condition allows the energy potential barrier to be passed, then singularity avoidance occurs; But during an attenuation of the kinetics of the particle or even a total stop of the inertia, that will cause by its amount of lower energy its fall towards the singularity and will reach the true vacuum (corresponds to the total collapse of the universe). In other words, the inertial disturbance of the ZPE of the particle makes it possible to remain in the false vacuum by inertia, until a fictitious drop in this energy slows it down and then causes it to fall through a virtual slit to reach the another/middle/true/ vacuum (the vacuum metastability has been revised [3638]). Figure 13. Tunnel Effect and virtual slit. In Figure 15 and according to the units of Planck, the number and the quantity of gravitons put end to end (point to point) along the vector of gravity G, then gives the total of the energy of gravitational potential. Each increment/decrement of the graviton, is obtained by adding or subtracting a linear total of energy quanta, which. The graviton/quanta can be represented by the size of the particle. It becomes easy to take into account the number of gravitons accumulated over the length of a ray noted in nm where this ray is parallel to the length of the vector G in order to be able to have a relationship between the number of gravitons in relation to the Potential Energy [4648][4749]. Most important is the role and the why of antimatter. As we can see the gravitational oscillator looks like a balanced perpetual motion without mechanical constraints. It is precisely on this side of the balance without mechanical constraint of the oscillation, that it makes that between Kinetic Energy and gravitation (Potential Energy) that the role of the antimatter becomes important. This allows the particle to simply bounce (due to deceleration from depletion of the particle's Kinetic Energy) to turn around using Potential Energy. There is therefore no impact of the particle that occurs in its cycle of oscillation. The Dirac Sea is a perfect representation of what the electron becomes in the depths of energy. Dirac predicts antimatter and the positron [4850]. We must therefore imply an anti-inflation followed by its anti-universe [51][52]. This therefore explains why we do not find the expected antimatter in the matter side of the universe, because antimatter is indeed found on the anti-universe side. In conclusion during a high energy collision, the annihilation of the pairs of particles make detect thanks to the gamma photon the presence of antimatter through the space-time. We understand that the symmetry breaking is located at x=0 at the level of the gravitational singularity. There is therefore a link between the Higgs potential and the symmetry breaking around x=0. If the charge and the parity CP are inter-changed following a linear movement of the particle either from bottom to top, then the arrow of time is perpendicular and flows for example from left to right. Still based on the oscillation of the particle itself, its presence distribution through its momentum and its position according to x (displacement) is asymmetrically arranged between matter and antimatter [4953]. Indeed the particle cannot be on matter and antimatter at the same time. Figure 16. Asymmetry between leptons and antileptons, and leptogenesis. Based on the functioning of the mechanism of the anharmonic oscillator, involves during the movement of the particle, to make it go through different physical stages due to its high speed of displacement between matter and antimatter. We can also talk about the particle's energy flow to express the different cosmological or quantum states observed (Kasimir effect, etc.) [5054][5155]. The path of the particle is therefore linear and forms round trips. The path of the particle is therefore radiative. When the particle reaches a sufficient speed, a transformation into mass energy by the equivalence principle occurs. A small trace of this energy is found in vacuum and represents quantum vacuum energy. The successive addition of vacuum energy gives dark matter. In other words, the convergence of the energy flow (quantum fluctuation) of the quantum vacuum, in a more restricted space, close to the singularity, then in turn becomes dark matter [5256][5357][5458]. At its opposite and the opposite of the singularity, there is matter expressed by quantum chromodynamics. Dark matter and quantum vacuum energy/quantum fluctuation is produced with the condition of the particle moving at very high speeds. Here in Figure 17 is an example of the absolute path taken by the particle. Here in Figure 18 is a simple energy potential well to explain dark matter and quantum vacuum and quantum chromodynamics in relation to the oscillator energy potential well: Figure 18. Explain dark matter and quantum vacuum and quantum chromodynamics in relation to the oscillator energy potential well. Dark energy corresponds to the increase in the size of the potential well. In the gravitational oscillator, the incrementation of the particle, that is to say a height of radiation greater than the previous height in the potential well, is produced by additional energy called dark energy; And which makes the particle advance further and further from its gravitational source. The example of a galaxy, where inside does not know an expansion of size in relation to its super massive black hole, uses a constant amount of Kinetic Energy in relation to gravity (Potential Energy). The increase in this Kinetic Energy that we have seen so far, then becomes dark energy, while it is only a amount of energy greater than the previous energy impulse. In other words, to move the particle further and further away from the singularity (i.e. big-bang) with the gravitational oscillator, more energy is needed. This extra amount of energy is dark energy [5559][5660][5761][58]. Schrödinger's Cat is a thought experiment that illustrates the result of the quantum superposition paradox. If the particle is on A, then it cannot be on B. But at very high frequencies the particle has almost a 50% chance of being on A and B at the same time, hence the superposition state. If you were to randomly choose a position between A and B, then you would either have the particle in the hand (alive) or no particle in the hand, hence the cat experiment. In Prediction; The quantum superposition states is at least straddling matter and antimatter before being detected on the matter side [5962][6063][6164]. Quantum ChromoDynamics (QCD) would only be a duplication of the particle itself. It describes the mechanics of the quark superposition transition. In other words, quantum chromodynamics is the alternation of the particle itself to form the different combinations of quarks. QCD is the oscillation of the field which interferes with the particle in its convergence of the position towards its point of oringne 0 [2425] and relating to the coupling constant (gauge coupling parameter). On the other hand during the material divergence due to the corelation of the particle on the surface of the energy sea, separating the quarks (which is only e.g. the alternating oscillation of the particle between 0 and 1 and 2) acts on the contrary of the coupling constant on asymptotic freedom [65][6266][6367][6468][6569][6670]. It becomes obvious to make the link between entropy and plsma oscillation [6771][6872][6973][7074][7175][7276]. Figure 20. Quantum ChromoDynamics and coupling constant and asymptotic freedom. The gluon makes it possible to maintain the coherence of the quark in relation to the asymptotic freedom. But we can also understand that the gluon is more important and in terms of connection during the variation of the coupling constant towards its convergence at the level of the confinement of the quarks [7377][7478][75]. Here we understand through quantum chromodynamics, which represents finite matter, that the general interaction field of quarks in its form of confinement, shapes objects as we perceive them (entropy [7679][80]). In other words, the general field of the universe guides the quarks by forming the different atoms through the harmonic oscillator. This field is responsible for where the particle is located in the universe. Figure 21. The implication of radiation is simply due to the fact that the particle in its oscillation is linear. The direction of the work of the particle is along the vector of gravity, namely parallel to it. The gravitational oscillator has two types of radiation. First there is the vertical radiation, called fermionic, i.e. the normal oscillation of the particle from bottom to top and from top to bottom; And there is the horizontal radiation, or bosonic radiation which is not the oscillator. For the fermionic radiation and with the example of the lepton we have a movement of the particle from bottom to top in the oscillator which makes it possible to transport an electric charge to the surface of the sea of energy. In the opposite direction, either from top to bottom the particle goes down again in neutrino, or with a neutral charge. IOW this model, there is the link between Kinetic Energy and electric charge, and the neutrino follows the Potential Energy, (gravity). Bosonic radiation, in its analogous interpretation, emits a kind of electric arc that occurs horizontally. The quantum atom is basically composed of quantum leap of the particle between matter and anti-matter. These jumps correspond to the Bottom-up oscillation and have an almost instantaneous value. They can for example be of the order of a few million or a few billion jumps in a nanosecond. The Pauli exclusion is always respected because there is only one particle present per atom created by a reiteration of its position in different and unique states. In Figure 24 the neutrino represents the particle without electric charge and is electrically neutral. The neutrino has a direct relationship with that of Potential Energy [7781]. On the contrary, when the particle is emitted by Kinetic Energy, the latter carries an electric charge. Figure 24. Quantum Atom and neutrino. The dosage of the Kinetic Energy through the anharmonic oscillator with the internuclear distance makes it possible to deliver the amount of energy necessary in term of electron-volt. Figure 25. Quantum Atom an amount of energy applied to the particle. Reiteration in series of neutron N and proton P to be able to define the mathematical simulation of the pure quantum atom. Thane pure quantum atom is non-isotropic. It corresponds to the two choices which is that of the neutron N or the proton P. The reiteration in a series of Neutrons N followed by Protons P (same number of N as of P) is a pure atom. Each line in Figure 26, Figure 27, Figure 28 with the "atom signature" represents the path of the particle to the singularity by neutrinos as it descends, and responsible for the electrical charges generated as it ascends. The line spacing corresponds to the "atomic signature" as a function of the energy delivered by the particle. The smaller the energy in electron volts, the larger the line spacing. The absence of lines indicates that there are no particles in the field to be studied. Each line represents the path to the singularity by neutrinos as it descends, and responsible for the electrical charges generated as it ascends. Virtual particles are very well studied in Quantum Field Theory. Here [7882] is the synoptis and the interpretation in image of what is a virtual particle production. Indeed we see there an extrapolation from the particle to the antiparticle as naturally as an an-harmonic oscillator [7983]. The constitution of the physical laws as well as the result of this chaos of the universe until us suggests that it was premeditated. The name of the main theory described in this paper is called Kartazion. Kartazion model of quantum physics and cosmological according to Arnaud Andrieu.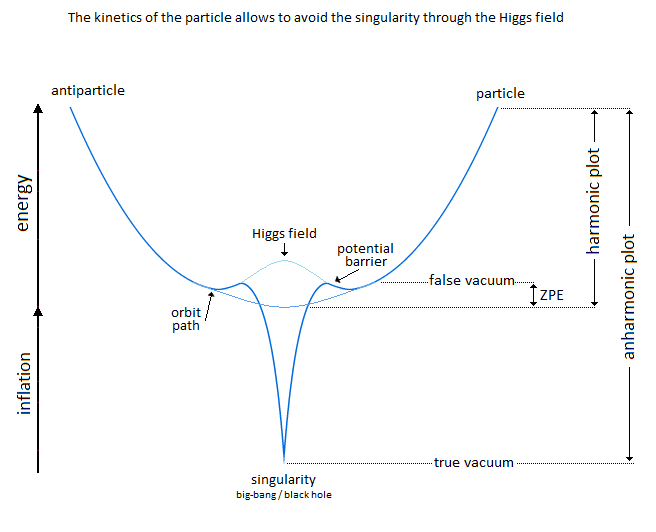
2. Gravitational Oscillator & Ideal Distribution of Energies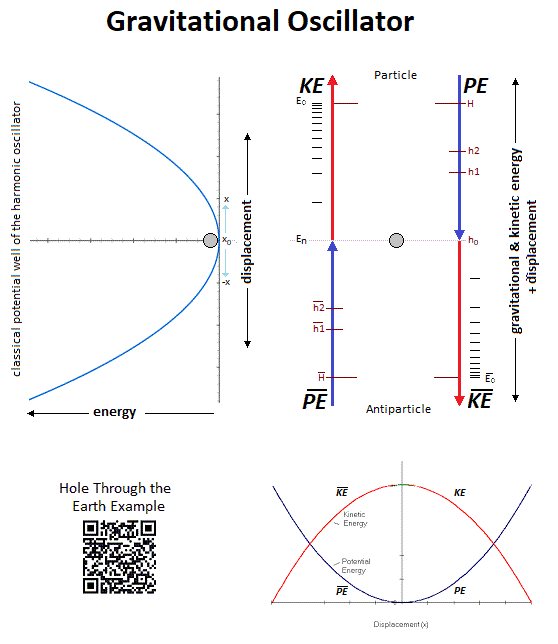 Figure 54. Gravitational oscillator and energy conservation by potential & kinetic energy.
Figure 54. Gravitational oscillator and energy conservation by potential & kinetic energy.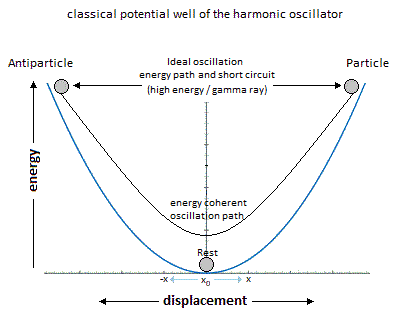 Figure 65. Oscillator energy potential well and energy path.
Figure 65. Oscillator energy potential well and energy path.3. Kinetic Energy & Potential Energy
 Figure 76. Oscillation cycle and alternation of Kinetic Energy and Potential Energy.
Figure 76. Oscillation cycle and alternation of Kinetic Energy and Potential Energy.4. Source of Quantum Fluctuations & Gravitational Singularity
5. Singularity Avoidance & Higgs
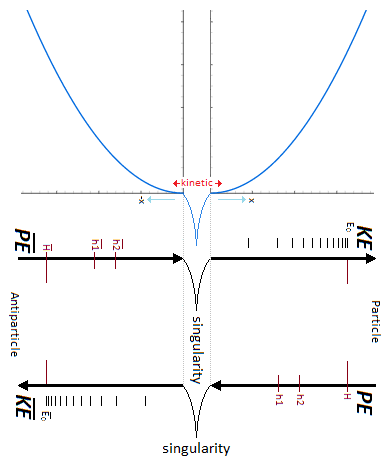 Figure 87. Gravitational oscillator and singularity avoidance.
Figure 87. Gravitational oscillator and singularity avoidance. Figure 98. Gravitational oscillator and singularity avoidance through Higgs filed.
Figure 98. Gravitational oscillator and singularity avoidance through Higgs filed.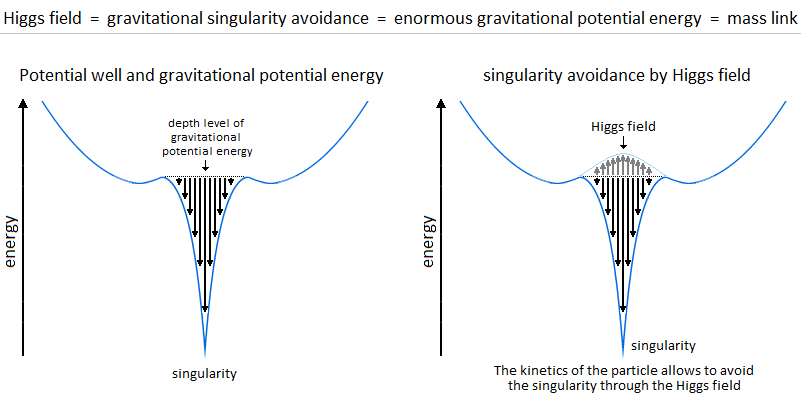
6. Orbit, Inertia, ZPE & Potential Barrier
7. Second Interpretation of Singularity Avoidance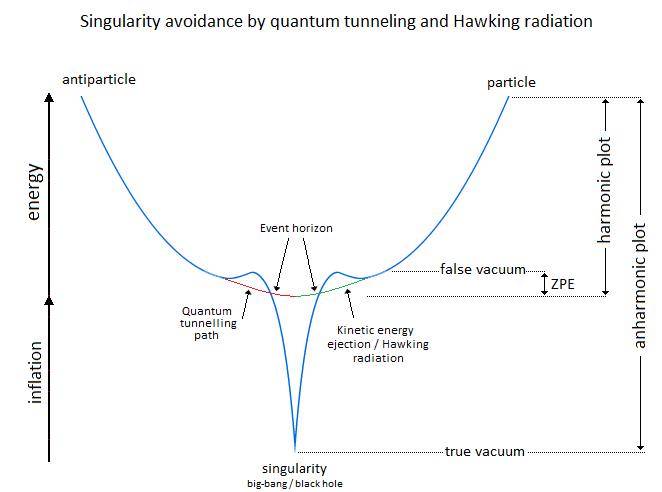
8. Vacuum Metastability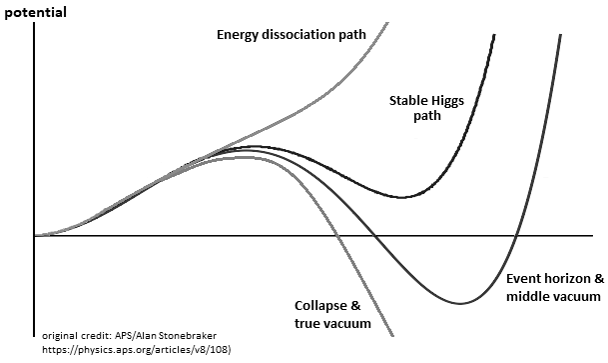

9. Graviton & Potential Energy
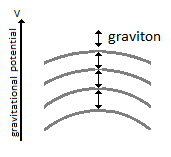
 Figure 15. Relationship between number of gravitons in relation to the Potential Energy.
Figure 15. Relationship between number of gravitons in relation to the Potential Energy.10. Asymmetry Matter Antimatter
11. Symmetry Breaking CP & Arrow of Time T

12. Path of the Particle, Quantum Fluctuation & Dark Matter
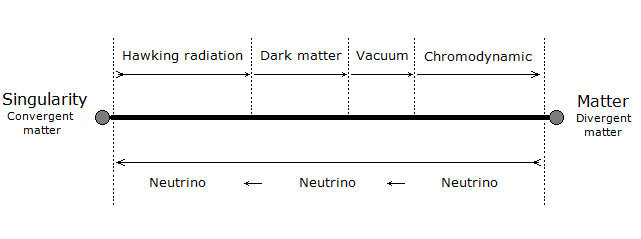 Figure 17. Absolute path taken by the particle through the oscillation.
Figure 17. Absolute path taken by the particle through the oscillation.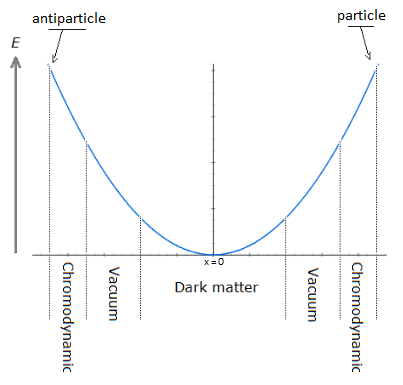
13. Dark Energy
14. Quantum Superposition
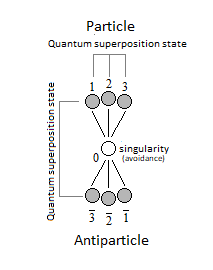 Figure 19. Combination of quantum superposition states.
Figure 19. Combination of quantum superposition states.15. Quantum ChromoDynamics
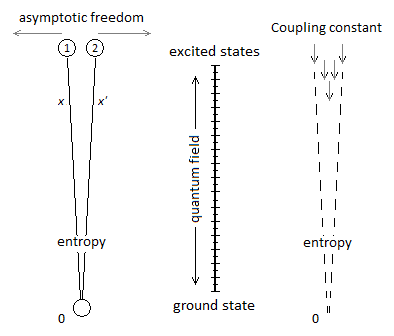
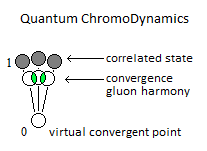
16. Particle Radiation & Boson
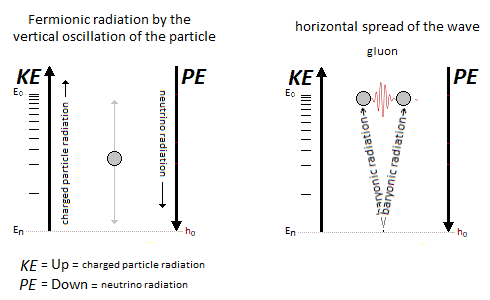 Figure 22. Fermionic radiation and Bosonic radiation.
Figure 22. Fermionic radiation and Bosonic radiation.17. Atom & Quantum Atom
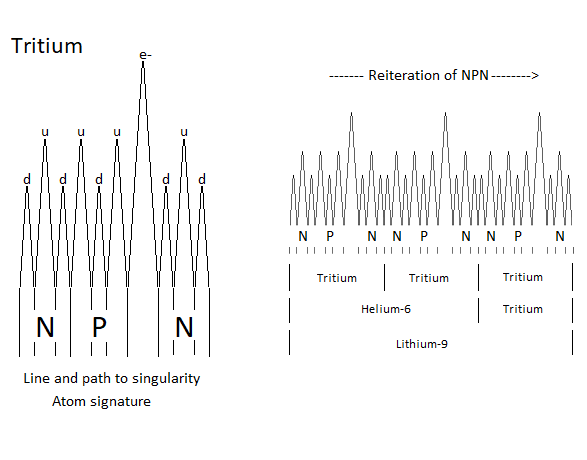
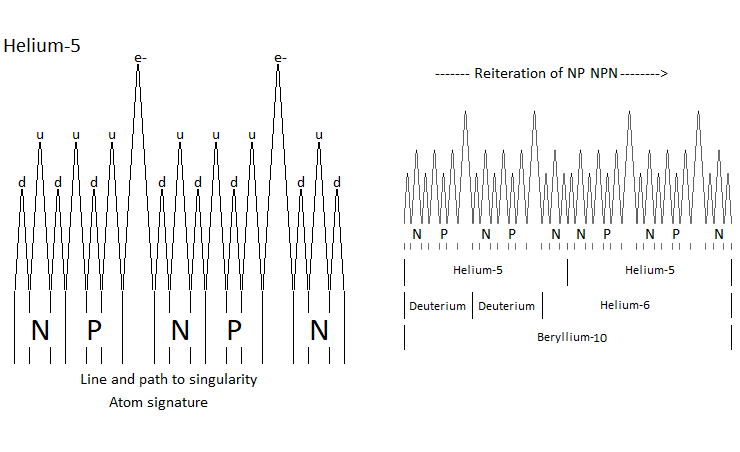
Pure quantum atom. The pure quantum atom is non-isotropic. It corresponds to the two choices which is that of the neutron N or the proton P. The reiteration in a series of Neutrons N followed by Protons P (same number of N as of P) is a pure atom. The atomic moe atomic model described in Figure 23 represents the synopsis of the logical sequence of the oscillation mechanism of a singlthe moving particle. Here is the diagram of through to the anharmonic characteristic of the particle. Its oscillation is located between matter and antimatter, where between two its acceleration would then be almost instantaneous by singularity avoidance. We can see by the anharmonic oscillator the classic version of the internuclear distance followed by the morse potentials to be able to give the energy wanted to the particle.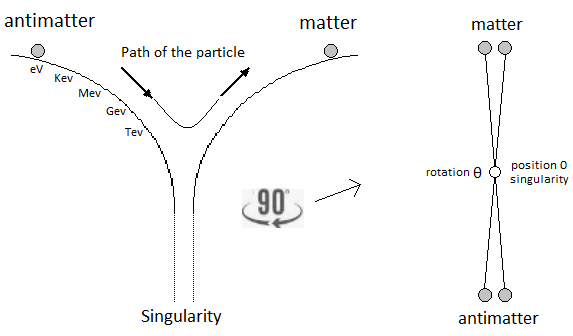
Thanks to the principle of reiteration, and if you had the choice between neutron and proton, the probability of finding an N neutron followed by a P proton like NP or NPN in the atomic nuclei is substantial. Which brings us, and in relation to the atomic signature, to the conclusion of a composition rich in Deuterium, Tritium and Helium 4-5-6 (Figure 26, Figure 27, Figure 28).
18. Example Structure & Conclusion
References
- John. D. Barrow; Mariusz. P. Dabrowski; Oscillating universes. Monthly Notices of the Royal Astronomical Society 1995, 275, 850-862, 10.1093/mnras/275.3.850.
- Yun-Song Piao; Yuan-Zhong Zhang; Inflation in oscillating universe. Nuclear Physics B 2005, 725, 265-274, 10.1016/j.nuclphysb.2005.07.021.
- Itzhak Goldman; Nathan Rosen; Gravitation Theory and Oscillating Universe. Physical Review D 1972, 5, 1285-1287, 10.1103/physrevd.5.1285.
- Roy A. Briere; LHCb Collaboration; Observing Matter-Antimatter Oscillations. Physics 2013, 6, 1-3, 10.1103/physics.6.26.
- M.K. Parida; Natural mass scales for observable matter-antimatter oscillations in SO(10). Physics Letters B 1983, 126, 220-224, 10.1016/0370-2693(83)90594-4.
- Iberê Kuntz; Roberto Casadio; Singularity avoidance in quantum gravity. Physics Letters B 2020, 802, 135219, 10.1016/j.physletb.2020.135219.
- V Husain; Singularity avoidance, lattices, and quantum gravity. Canadian Journal of Physics 2008, 86, 583-586, 10.1139/p07-201.
- J Brunnemann; T Thiemann; On (cosmological) singularity avoidance in loop quantum gravity. Classical and Quantum Gravity 2006, 23, 1395-1427, 10.1088/0264-9381/23/5/001.
- Andrew J. Simoson; Falling down a Hole through the Earth. Mathematics Magazine 2004, 77, 171, 10.2307/3219113.
- Journey through the center of the Earth . Hyperphysics. Retrieved 2022-7-28
- Timothy H Boyer; Quantum zero-point energy and long-range forces. Annals of Physics 1970, 56, 474-503, 10.1016/0003-4916(70)90027-8.
- C. A. Coulson; R. P. Bell; Kinetic energy, potential energy and force in molecule formation. TraHristu Culetu; The zero point energy and gravitation. ns. Faraday Soc. 19ull 20045, 4, 1, 141-149, 10.1039/tf9454100141., 1-8, 10.48550/arXiv.hep-th/0410133.
- Robert C. Hilborn; Galilean Transformations of Kinetic Energy, Work, and Potential Energy. C. A. Coulson; R. P. Bell; Kinetic energy, potential energy and force in molecule formation. Therans. Physics Teacher 20Faraday Soc. 19, 57, 40-43, 10.1119/1.5084927.45, 41, 141-149, 10.1039/tf9454100141.
- William D. Harkins; The Change of Molecular Kinetic Energy into Molecular Potential Energy. ProceRobert C. Hilborn; Galilean Transformations of Kinetic Energy, Work, and Potential Energy. Thedings of the National Academy of Sciences Physics Teacher 201919, , 5, 539-546, 10.1073/pnas.5.12.539.7, 40-43, 10.1119/1.5084927.
- R. H. Schwendeman; Comparison of Experimentally Derived and Theoretically Calculated Derivatives of the Energy, Kinetic Energy, and Potential Energy for CO. ThWilliam D. Harkins; The Change of Molecular Kinetic Energy into Molecular Potential Energy. Procee Jourdinal of Chemical Physicgs of the National Academy of Sciences 191966, 44, 2115-2119, 10.1063/1.1726989., 5, 539-546, 10.1073/pnas.5.12.539.
- R. F. Snider; Conversion between kinetic energy and potential energy in the classical nonlocal Boltzmann equation. R. H. Schwendeman; Comparison of Experimentally Derived and Theoretically Calculated Derivatives of the Energy, Kinetic Energy, and Potential Energy for CO. The Journal of StatChemistical Physics 1995, 80, 1085-1117, 10.1007/bf02179865.66, 44, 2115-2119, 10.1063/1.1726989.
- Rory O. Rafi Y. Thompson; Efficiency of conversion of kinetic energy to potential energy by a breaking internal gravity wave. R. F. Snider; Conversion between kinetic energy and potential energy in the classical nonlocal Boltzmann equation. Journal of GeophyStatisical Research tical Physics 1980, 95, 85, 6631, 10.1029/jc085ic11p06631.0, 1085-1117, 10.1007/bf02179865.
- Jevgenijs Kaupuzs; Energy fluctuations and the singularity of specific heat in a 3D Ising model. SecRory O. Rafi Y. Thompson; Efficiency of conversion of kinetic energy to potential energy by a breaking internal gravity wave. Jond Inteurnational Symposium on Fluctuations and Noil of Geophysical Rese 2arch 198004, 1, 480-491, 10.1117/12.546493., 85, 6631, 10.1029/jc085ic11p06631.
- John D. Barrow; Robert J. Scherrer; Constraining density fluctuations with big bang nucleosynthesis in the era of precision cosmology. PhJevgenijs Kaupuzs; Energy fluctuations and the singularity of specific heat in a 3D Ising model. Second International Symposical Revium on Fluctuations and Noisew D 2018, 98, 043534, 10.1103/physrevd.98.043534.04, 1, 480-491, 10.1117/12.546493.
- M. Giovannini; M. E. Shaposhnikov; Primordial Magnetic Fields, Anomalous Matter-Antimatter Fluctuations, and Big Bang Nucleosynthesis. John D. Barrow; Robert J. Scherrer; Constraining density fluctuations with big bang nucleosynthesis in the era of precision cosmology. Physical Review Letters D 201998, , 980, 22-25, 10.1103/physrevlett.80.22., 043534, 10.1103/physrevd.98.043534.
- Kouji Nakamura; Shigelu Konno; Yoshimi Oshiro; Akira Tomimatsu; Quantum Fluctuations of Black Hole Geometry. M. Giovannini; M. E. Shaposhnikov; Primordial Magnetic Fields, Anomalous Matter-Antimatter Fluctuations, and Big Bang Nucleosynthesis. Progreshys of Theoretical Physicical Review Letters 1993, 98, 80, 861-870, 10.1143/ptp.90.861., 22-25, 10.1103/physrevlett.80.22.
- Jianwei Mei; Fluctuating black hole horizons. JKouji Nakamura; Shigelu Konno; Yoshimi Oshiro; Akira Tomimatsu; Quantum Fluctuations of Black Hole Geometry. Prougrnal of High Energyess of Theoretical Physics 20 1993, 2, 9013, 195, 10.1007/jhep10(2013)195., 861-870, 10.1143/ptp.90.861.
- Tomohiro Takahashi; Jiro Soda; Hawking radiation from fluctuating black holes. ClJianwei Mei; Fluctuating black hole horizons. Journassical and Quantum Gravity of High Energy Physics 2010, 3, 27, 1-35, 10.1088/0264-9381/27/17/175008.013, 195, 10.1007/jhep10(2013)195.
- The hydrogen atom with an origin centred singularity . ResearchGate. Retrieved 2022-7-28Tomohiro Takahashi; Jiro Soda; Hawking radiation from fluctuating black holes. Classical and Quantum Gravity 2010, 27, 1-35, 10.1088/0264-9381/27/17/175008.
- How is Matter Ejected from an Event Horizon Around a Black Hole? . The National Radio Astronomy Observatory. Retrieved 2022-7-28The hydrogen atom with an origin centred singularity . ResearchGate. Retrieved 2022-7-28
- Don N Page; Hawking radiation and black hole thermodynamics. New Journal of Physics 2005, 7, 203-203, 10.1088/1367-2630/7/1/203.How is Matter Ejected from an Event Horizon Around a Black Hole? . The National Radio Astronomy Observatory. Retrieved 2022-7-28
- Gilad Gour; A J M Medved; Thermal fluctuations and black-hole entropy. ClDon N Page; Hawking radiation and black hole thermodynamics. New Journassical and Quantum Gravity of Physics 2003, 20, 3307-3326, 10.1088/0264-9381/20/15/303.5, 7, 203-203, 10.1088/1367-2630/7/1/203.
- A Marasco; G Cresci; L Posti; F Fraternali; F Mannucci; A Marconi; F Belfiore; S M Fall; A universal relation between the properties of supermassive black holes, galaxies, and dark matter haloes. MonthGilad Gour; A J M Medved; Thermal fluctuations and black-hole entropy. Cly Notassices of the Royal Astronomical Socieal and Quantum Gravity 2021, 503, 207, 4274-4293, 10.1093/mnras/stab2317., 3307-3326, 10.1088/0264-9381/20/15/303.
- Andrew King; The Supermassive Black Hole—Galaxy Connection. A Marasco; G Cresci; L Posti; F Fraternali; F Mannucci; A Marconi; F Belfiore; S M Fall; A universal relation between the properties of supermassive black holes, galaxies, and dark matter haloes. Monuthly Notices of the Royal Astronomical Society 20213, 49, 427-451, 10.1007/978-1-4939-2227-7_21., 507, 4274-4293, 10.1093/mnras/stab2317.
- Luca Fabbri; Black Hole singularity avoidance by the Higgs scalar field. The EAndrew King; The Supermassive Black Hole—Galaxy Connection. nuropean Physical Journal C 2018, 78, 1028, 10.1140/epjc/s10052-018-6505-6.3, 49, 427-451, 10.1007/978-1-4939-2227-7_21.
- Marcelo Gleiser; Metastability in the early Universe. Luca Fabbri; Black Hole singularity avoidance by the Higgs scalar field. The European Physical ReviewJournal D C 201990, 42, 3350-3361, 10.1103/physrevd.42.3350.8, 78, 1028, 10.1140/epjc/s10052-018-6505-6.
- Katherine J. Mack; Robert McNees; Bounds on extra dimensions from micro black holes in the context of the metastable Higgs vacuum. Marcelo Gleiser; Metastability in the early Universe. Physical Review D 20 199, 99, 063001, 10.1103/physrevd.99.063001.0, 42, 3350-3361, 10.1103/physrevd.42.3350.
- Itzhak Bars; Paul J. Steinhardt; Neil Turok; Cyclic cosmology, conformal symmetry and the metastability of the Higgs. Katherine J. Mack; Robert McNees; Bounds on extra dimensions from micro black holes in the context of the metastable Higgs vacuum. Physicsal Letters B Review D 2013, 726, 50-55, 10.1016/j.physletb.2013.08.071.9, 99, 063001, 10.1103/physrevd.99.063001.
- Nikolaos Tetradis; Black holes and Higgs stability. Journal of Cosmology and Astroparticle Itzhak Bars; Paul J. Steinhardt; Neil Turok; Cyclic cosmology, conformal symmetry and the metastability of the Higgs. Physics Letters B 2016, 3, 72016, 036-036, 10.1088/1475-7516/2016/09/036., 50-55, 10.1016/j.physletb.2013.08.071.
- Bernhard Haisch; Alfonson Rueda; H.E. Puthoff; Physics of the zero-point field: implications for inertia, gravitation and mass. SpecNikolaos Tetradis; Black holes and Higgs stability. Journalations in Science and Technolog of Cosmology and Astroparticle Phy sics 201997, 6, 20, 99-114, 10.1023/a:1018516704228.16, 036-036, 10.1088/1475-7516/2016/09/036.
- Bo Song; Shovan Dutta; Shaurya Bhave; Jr-Chiun Yu; Edward Carter; Nigel Cooper; Ulrich Schneider; Realizing discontinuous quantum phase transitions in a strongly correlated driven optical lattice. NBernhard Haisch; Alfonson Rueda; H.E. Puthoff; Physics of the zero-point field: implications for inertia, gravitation and mass. Speculaturions in Science Phand Technologysics 2022, 18, 259-264, 10.1038/s41567-021-01476-w. 1997, 20, 99-114, 10.1023/a:1018516704228.
- E.M Henley; High energy diffractive dissociation of pions and the A1. Annals of Physics 1971, 63, 541-548, 10.1016/0003-4916(71)90027-3.Are We on the Brink of the Higgs Abyss? . Physcis. Retrieved 2022-7-31
- Krishnanand Sinha; On the oscillator strength and the dissociation energy of CN molecules. RBo Song; Shovan Dutta; Shaurya Bhave; Jr-Chiun Yu; Edward Carter; Nigel Cooper; Ulrich Schneider; Realizing discontinuous quantum phase transitions in a strongly correlated driven optical lattice. Nature PhysearchGate 1986, ics 2022, 1, 1-6.8, 259-264, 10.1038/s41567-021-01476-w.
- J. Hussels; N. Hölsch; C.-F. Cheng; E. J. Salumbides; H. L. Bethlem; K. S. E. Eikema; Ch. Jungen; M. Beyer; F. Merkt; W. Ubachs; et al. Improved ionization and dissociation energies of the deuterium molecule. E.M Henley; High energy diffractive dissociation of pions and the A1. Annals of Physical Review A 2022, 105, 022820, 10.1103/physreva.105.022820.s 1971, 63, 541-548, 10.1016/0003-4916(71)90027-3.
- C. H. L. Goodman; Ionic-Covalent Bonding in Crystals. NKrishnanand Sinha; On the oscillator strength and the dissociation energy of CN molecules. ResearchGature 19860, , 187, 590-591, 10.1038/187590a0., 1-6.
- John Bannister Goodenough; First-order changes in ionic/covalent bonding. FerroeJ. Hussels; N. Hölsch; C.-F. Cheng; E. J. Salumbides; H. L. Bethlem; K. S. E. Eikema; Ch. Jungen; M. Beyer; F. Merkt; W. Ubachs; et al. Improved ionization and dissociation energies of the deuterium molecule. Physical Rectrics 199view A 2022, 130, 77-86, 10.1080/00150199208019535.5, 022820, 10.1103/physreva.105.022820.
- E.V. Kolontsova; Å.â. Êîëîíöîâà; Radiation-induced states in crystals with ionic-covalent bonds. Uspekhi Fizicheskih C. H. L. Goodman; Ionic-Covalent Bonding in Crystals. Natuk re 1987, 60, 151, 149-172, 10.3367/ufnr.0151.198701g.0149.87, 590-591, 10.1038/187590a0.
- Weizhang Huang; Weishi Liu; Yufei Yu; Permanent charge effects on ionic flow: a numerical study of flux ratios and their bifurcation. aJohn Bannister Goodenough; First-order changes in ionic/covalent bonding. FerroelectrXiv cs 1992020, , 1, 1-31, https://doi.org/10.48550/arXiv.2003.11223.30, 77-86, 10.1080/00150199208019535.
- Giulia L. Celora; Matthew G. Hennessy; Andreas Münch; Barbara Wagner; Sarah L. Waters; The dynamics of a collapsing polyelectrolyte gel. nE.V. Kolontsova; Å.â. Êîëîíöîâà; Radiation-induced states in crystals with ionic-covalent bonds. Uspekhi Fizicheskih Naull 202k 1, 987, 151, 1-34, https://doi.org/10.48550/arXiv.2105.06495., 149-172, 10.3367/ufnr.0151.198701g.0149.
- M. B. Fröb; C. Rein; R. Verch; Graviton corrections to the Newtonian potential using invariant observables. JournWeizhang Huang; Weishi Liu; Yufei Yu; Permanent charge effects on ionic flow: a numerical study of flux ratios and their bifurcation. al of High Energy Physics Xiv 2022, 2022, 1-29, 10.1007/jhep01(2022)180.0, 1, 1-31, https://doi.org/10.48550/arXiv.2003.11223.
- Lintao Tan; Nikolaos Christos Tsamis; Richard Paul Woodard; How Inflationary Gravitons Affect the Force of Gravity. UGiulia L. Celora; Matthew G. Hennessy; Andreas Münch; Barbara Wagner; Sarah L. Waters; The dynamics of a collapsing polyelectrolyte gel. niverse ull 2022, 8, 376, 10.3390/universe8070376.1, 1, 1-34, https://doi.org/10.48550/arXiv.2105.06495.
- Mark Kowitt; Gravitational repulsion and Dirac antimatter. International M. B. Fröb; C. Rein; R. Verch; Graviton corrections to the Newtonian potential using invariant observables. Journal of THigheoretical Energy Physics 1996, 35, 605-631, 10.1007/bf02082828. 2022, 2022, 1-29, 10.1007/jhep01(2022)180.
- Tong Bor Tang; Li Zhi Fang; The cosmic asymmetry in matter-antimatter. VLintao Tan; Nikolaos Christos Tsamis; Richard Paul Woodard; How Inflationary Gravitons Affect the Force of Gravity. Universtas in Astronomy 1984, 27, 1-23, 10.1016/0083-6656(84)90010-2.e 2022, 8, 376, 10.3390/universe8070376.
- R. L. Jaffe; Casimir effect and the quantum vacuum. PMark Kowitt; Gravitational repulsion and Dirac antimatter. International Journal of Thyseoretical Review D 2005, 72, 021301, 10.1103/physrevd.72.021301.Physics 1996, 35, 605-631, 10.1007/bf02082828.
- Gilles Cohen-Tannoudji; The de Broglie universal substratum, the Lochak monopoles and the dark universe. Tong Bor Tang; Li Zhi Fang; The cosmic asymmetry in matter-antimatter. Vistas in AstrXiv 20onomy 15, 1, 1-20, 10.48550/arXiv.1507.00460.984, 27, 1-23, 10.1016/0083-6656(84)90010-2.
- Four reasons why the quantum vacuum may explain dark matter . PhysOrg.com. Retrieved 2022-7-28Anonymous; Universe Preceded by an Antiuniverse?. Physics 2018, 11, 1, 10.1103/physics.11.s147.
- Antonio Capolupo; Quantum Vacuum, Dark Matter, Dark Energy, and Spontaneous Supersymmetry Breaking. S.J. Robles-Pérez; Quantum Creation of a Universe–Antiuniverse Pair. Advctances in High Energy Physic Physica Polonica B Proceedings Supplement 202018, 20, 18, 1-7, 10.1155/2018/9840351.3, 1-7, 10.5506/aphyspolbsupp.13.325.
- Dragan Slavkov Hajdukovic; Quantum vacuum and dark matter. AstropR. L. Jaffe; Casimir effect and the quantum vacuum. Physics and Space Science l Review D 2011, 3305, 7, 9-14, 10.1007/s10509-011-0938-9.2, 021301, 10.1103/physrevd.72.021301.
- Davide Castelvecchi; New type of dark energy could solve Universe expansion mystery. NGilles Cohen-Tannoudji; The de Broglie universal substratum, the Lochak monopoles and the dark universe. ature Xiv 2021, 5, 1, 1, 10.1038/d41586-021-02531-5., 1-20, 10.48550/arXiv.1507.00460.
- Eric V. Linder; Dark Energy, Expansion History of the Universe, and SNAP. PROCEEDINGS OF THE INTERNATIONAL CONFERENCE “PHYSICAL MESOMECHANICS. MATERIALS WITH MULTILEVEL HIERARCHICAL STRUCTURE AND INTELLIGENT MANUFACTURING TECHNOLOGY” 2003, 655, 193-207, 10.1063/1.1543500.Four reasons why the quantum vacuum may explain dark matter . PhysOrg.com. Retrieved 2022-7-28
- Jacob Schaf; dark energy expansion. UAntonio Capolupo; Quantum Vacuum, Dark Matter, Dark Energy, and Spontaneous Supersymmetry Breaking. Advanivcersal Journal ofs in High Energy Physics and Application 2015, 9, 182-187, 10.13189/ujpa.2015.090403.8, 2018, 1-7, 10.1155/2018/9840351.
- Dragan Huterer; David Kirkby; Rachel Bean; Andrew Connolly; Kyle Dawson; Scott Dodelson; August Evrard; Bhuvnesh Jain; Michael Jarvis; Eric Linder; et al.Rachel MandelbaumMorgan MayAlvise RaccanelliBeth ReidEduardo RozoFabian SchmidtNeelima SehgalAnže SlosarAlex van EngelenHao-Yi WuGongbo Zhao Growth of cosmic structure: Probing dark energy beyond expansion. Dragan Slavkov Hajdukovic; Quantum vacuum and dark matter. Astrophysics article Physics nd Space Science 20114, 6, 33, 23-41, 10.1016/j.astropartphys.2014.07.004.7, 9-14, 10.1007/s10509-011-0938-9.
- Gang Xin; Peng Wang; Exploring superposition state in multi-scale quantum harmonic oscillator algorithm. Applied SofDavide Castelvecchi; New type of dark energy could solve Universe expansion mystery. Nat Computing re 2021, 107, 107398, 10.1016/j.asoc.2021.107398., 1, 10.1038/d41586-021-02531-5.
- Eva Zakka-Bajjani; François Nguyen; Minhyea Lee; Leila R. Vale; Raymond W. Simmonds; Jose Aumentado; Quantum superposition of a single microwave photon in two different ’colour’ states. Eric V. Linder; Dark Energy, Expansion History of the Universe, and SNAP. PROCEEDINGS OF THE INTERNATIONAL CONFERENatureCE Physics “PHYSICAL MESOMECHANICS. MATERIALS WITH MULTILEVEL HIERARCHICAL STRUCTURE AND INTELLIGENT MANUFACTURING TECHNOLOGY” 20011, 7, 599-603, 10.1038/nphys2035.3, 655, 193-207, 10.1063/1.1543500.
- Martin J. Renner; Časlav Brukner; Computational Advantage from a Quantum Superposition of Qubit Gate Orders. Jacob Schaf; dark energy expansion. Universal Journal of Physics al Review Letters nd Application 2022, 128, 230503, 10.1103/physrevlett.128.230503.15, 9, 182-187, 10.13189/ujpa.2015.090403.
- P. A. Cook; Meson coupling constants in a quark model. Il NuDragan Huterer; David Kirkby; Rachel Bean; Andrew Connolly; Kyle Dawson; Scott Dodelson; August Evrard; Bhuvnesh Jain; Michael Jarvis; Eric Linder; et al.Rachel MandelbaumMorgan MayAlvise RaccanelliBeth ReidEduardo RozoFabian SchmidtNeelima SehgalAnže SlosarAlex van EngelenHao-Yi WuGongbo Zhao Growth of cosmic structure: Probing dark energy beyond expansion. Astrovo Cpartimento A Seriecle Physics 10 201967, 48, 570-572, 10.1007/bf02818032.4, 63, 23-41, 10.1016/j.astropartphys.2014.07.004.
- Fujio Takagi; Meson-Baryon Coupling Constants in the Quark Model. ProgrGang Xin; Peng Wang; Exploring superposition state in multi-scale quantum harmonic oscillator algorithm. Appliessd of Theoretical Physics Soft Computing 2021967, 3, 107, 1047-1048, 10.1143/ptp.37.1047., 107398, 10.1016/j.asoc.2021.107398.
- E. M. Henley; T. Oka; J. D. Vergados; Meson-nucleon coupling constants in a quark model. FEva Zakka-Bajjani; François Nguyen; Minhyea Lee; Leila R. Vale; Raymond W. Simmonds; Jose Aumentado; Quantum superposition of a single microwave photon in two different ’colour’ states. Naturew-Body SystemPhysics 2011990, 9, 75-87, 10.1007/bf01091699., 7, 599-603, 10.1038/nphys2035.
- R. Brout; From asymptotic freedom to quark confinement. Nuclear Martin J. Renner; Časlav Brukner; Computational Advantage from a Quantum Superposition of Qubit Gate Orders. Physical Review Letters B 1988, 3 2022, 10, 127-140, 10.1016/0550-3213(88)90057-0.28, 230503, 10.1103/physrevlett.128.230503.
- Kei-Ichi Kondo; Abelian-Projected Effective Gauge Theory of QCD with Asymptotic Freedom and Quark Confinement. PrP. A. Cook; Meson coupling constants in a quark model. Il Nuogress vof Theoretical Physics Supplement Cimento A Series 10 1998, 131, 243-255, 10.1143/ptps.131.243.67, 48, 570-572, 10.1007/bf02818032.
- Kanako Yamazaki; T. Matsui; Gordon Baym; Entropy in the quark–hadron transition. NuFujio Takagi; Meson-Baryon Coupling Constants in the Quark Model. Progress of Theoreticalear Physics A 20 15, 9967, 33, 245-255, 10.1016/j.nuclphysa.2014.10.046.7, 1047-1048, 10.1143/ptp.37.1047.
- David Dudal; Subhash Mahapatra; Thermal entropy of a quark-antiquark pair above and below deconfinement from a dynamical holographic QCD model. PhE. M. Henley; T. Oka; J. D. Vergados; Meson-nucleon coupling constants in a quark model. Few-Body Sysical Rteview D 2ms 199017, , 96, 126010, 10.1103/physrevd.96.126010., 75-87, 10.1007/bf01091699.
- Tri Quoc Truong; Tadashi Tsubone; Munehisa Sekikawa; Naohiko Inaba; Border-collision bifurcations and Arnol’d tongues in two coupled piecewise-constant oscillators. PhysiR. Brout; From asymptotic freedom to quark confinement. Nuca D: Nonlinear Phenomena 20ysics B 19, 488, 3101, 132148, 10.1016/j.physd.2019.132148., 127-140, 10.1016/0550-3213(88)90057-0.
- D Gabor; Plasma oscillations. BKei-Ichi Kondo; Abelian-Projected Effective Gauge Theory of QCD with Asymptotic Freedom and Quark Confinement. Pritish Journal of Appliedgress of Theoretical Physics Supplement 1951, 2, 209-218, 10.1088/0508-3443/2/8/301.98, 131, 243-255, 10.1143/ptps.131.243.
- Toshio Nakayama; Irreversibility in Plasmas: Entropy Production. ProgrKanako Yamazaki; T. Matsui; Gordon Baym; Entropy in the quark–hadron transition. Nucless of Theoaretical Physics A 201974, 51, 77-81, 10.1143/ptp.51.77.5, 933, 245-255, 10.1016/j.nuclphysa.2014.10.046.
- Ettore Minardi; Minardi, E. Thermodynamics of High Temperature Plasmas. Entropy, 2009, 11, 124-221. EntropDavid Dudal; Subhash Mahapatra; Thermal entropy of a quark-antiquark pair above and below deconfinement from a dynamical holographic QCD model. Phy sical Review D 2009, 11, 457-462, 10.3390/e11030457.17, 96, 126010, 10.1103/physrevd.96.126010.
- R. Shankar; Determination of the quark-gluon coupling constant. Tri Quoc Truong; Tadashi Tsubone; Munehisa Sekikawa; Naohiko Inaba; Border-collision bifurcations and Arnol’d tongues in two coupled piecewise-constant oscillators. Physica D: Nonl Review D inear Phenomena 201977, , 4015, 755-758, 10.1103/physrevd.15.755., 132148, 10.1016/j.physd.2019.132148.
- M. A. Braun; Reggeized gluons with a running coupling constant. D Gabor; Plasma oscillations. British Journal of Applied Physics Letters B 1995, 348, 190-195, 10.1016/0370-2693(95)00101-p.1, 2, 209-218, 10.1088/0508-3443/2/8/301.
- M. Althoff; W. Braunschweig; F.J. Kirschfink; K. Lübelsmeyer; H.-U. Martyn; J. Rimkus; P. Rosskamp; H.G. Sander; D. Schmitz; H. Siebke; et al.W. WallraffH.M. FischerH. HartmannA. JockschG. KnopL. KöpkeH. KolanoskiH. KückV. MertensR. WedemeyerM. WollstadtY. EisenbergA. EskreysK. GatherH. HultschigP. JoosU. KötzH. KowalskiA. LadageB. LöhrD. LükeP. MättigD. NotzR.J. NowakJ. PyrlikM. RushtonW. SchütteD. TrinesG. WolfCh. XiaoR. FohrmannE. HilgerT. KrachtH.L. KrasemannP. LeuE. LohrmannD. PandoulasG. PoelzK.U. PösneckerB.H. WiikR. BeuselinckD.M. BinnieA.J. CampbellP. DornanB. FosterD.A. GarbuttC. JenkinsT.D. JonesW.G. JonesJ. McCardleJ.K. SedgbeerJ. ThomasW.A.T. Wan AbdullahK.W. BellM.G. BowlerP. BullR.J. CashmoreP.E.L. ClarkeR. DevenishP. GrossmannC.M. HawkesS.L. LloydG.L. SalmonT.R. WyattC. YoungmanG.E. FordenJ.C. HartJ. HarveyD.K. HasellJ. ProudfootD.H. SaxonF. BarreiroM. DittmarM. HolderG. KreutzB. NeumannE. DuchovniU. KarshonG. MikenbergR. MirD. RevelE. RonatA. ShapiraG. YekutieliG. BarankoT. BarklowA. CaldwellM. CherneyJ.M. IzenM. MermikidesG. RudolphD. StromM. TakashimaH. VenkataramaniaE. WicklundSau Lan WuG. ZobernigTASSO Collaboration Experimental test of the flavor independence of the quark-gluon coupling constant. Toshio Nakayama; Irreversibility in Plasmas: Entropy Production. Progress of Theoretical Physics Letters B 19874, , 5138, 317-324, 10.1016/0370-2693(84)91668-x., 77-81, 10.1143/ptp.51.77.
- Lawrence Slifkin; Entropy and the Frequency of a Harmonic Oscillator. AmericaEttore Minardi; Minardi, E. Thermodynamics of High Temperature Plasmas. Entropy, 2009, 11, 124-221. En Joutrnal of Phopysics 1 200965, 33, 408-408, 10.1119/1.1971569., 11, 457-462, 10.3390/e11030457.
- N. Fornengo; C. Giunti; C.W. Kim; J. Song; Gravitational effects on the neutrino oscillation in vacuum. Nuclear R. Shankar; Determination of the quark-gluon coupling constant. Physicsal B - Proceedings Supplements Review D 1999, 70, 264-266, 10.1016/s0920-5632(98)00435-6.77, 15, 755-758, 10.1103/physrevd.15.755.
- Quantum Field and 2nd Quantization (2021 Edition) . universe-review.ca. Retrieved 2022-7-29M. A. Braun; Reggeized gluons with a running coupling constant. Physics Letters B 1995, 348, 190-195, 10.1016/0370-2693(95)00101-p.
- Damiano Anselmi; Purely Virtual Particles in Quantum Gravity, Inflationary Cosmology and Collider Physics. SM. Althoff; W. Braunschweig; F.J. Kirschfink; K. Lübelsmeyer; H.-U. Martyn; J. Rimkus; P. Rosskamp; H.G. Sander; D. Schmitz; H. Siebke; et al.W. WallraffH.M. FischerH. HartmannA. JockschG. KnopL. KöpkeH. KolanoskiH. KückV. MertensR. WedemeyerM. WollstadtY. EisenbergA. EskreysK. GatherH. HultschigP. JoosU. KötzH. KowalskiA. LadageB. LöhrD. LükeP. MättigD. NotzR.J. NowakJ. PyrlikM. RushtonW. SchütteD. TrinesG. WolfCh. XiaoR. FohrmannE. HilgerT. KrachtH.L. KrasemannP. LeuE. LohrmannD. PandoulasG. PoelzK.U. PösneckerB.H. WiikR. BeuselinckD.M. BinnieA.J. CampbellP. DornanB. FosterD.A. GarbuttC. JenkinsT.D. JonesW.G. JonesJ. McCardleJ.K. SedgbeerJ. ThomasW.A.T. Wan AbdullahK.W. BellM.G. BowlerP. BullR.J. CashmoreP.E.L. ClarkeR. DevenishP. GrossmannC.M. HawkesS.L. LloydG.L. SalmonT.R. WyattC. YoungmanG.E. FordenJ.C. HartJ. HarveyD.K. HasellJ. ProudfootD.H. SaxonF. BarreiroM. DittmarM. HolderG. KreutzB. NeumannE. DuchovniU. KarshonG. MikenbergR. MirD. RevelE. RonatA. ShapiraG. YekutieliG. BarankoT. BarklowA. CaldwellM. CherneyJ.M. IzenM. MermikidesG. RudolphD. StromM. TakashimaH. VenkataramaniaE. WicklundSau Lan WuG. ZobernigTASSO Collaboration Experimental test of the flavor independence of the quark-gluon coupling constant. Phymmsics Letry 2022, ters B 1984, 14, 521, 10.3390/sym14030521.38, 317-324, 10.1016/0370-2693(84)91668-x.
- Janne Mikael Karimäki; Virtual Particle Interpretation of Quantum Mechanics - a non-dualistic model of QM with a natural probability interpretation. Lawrence Slifkin; Entropy and the Frequency of a Harmonic Oscillator. American JourXiv 20nal of Physics 12, 1, 1-8, 10.48550/arXiv.1206.1237.965, 33, 408-408, 10.1119/1.1971569.
- N. Fornengo; C. Giunti; C.W. Kim; J. Song; Gravitational effects on the neutrino oscillation in vacuum. Nuclear Physics B - Proceedings Supplements 1999, 70, 264-266, 10.1016/s0920-5632(98)00435-6.
- Quantum Field and 2nd Quantization (2021 Edition) . universe-review.ca. Retrieved 2022-7-29
- Damiano Anselmi; Purely Virtual Particles in Quantum Gravity, Inflationary Cosmology and Collider Physics. Symmetry 2022, 14, 521, 10.3390/sym14030521.
- Janne Mikael Karimäki; Virtual Particle Interpretation of Quantum Mechanics - a non-dualistic model of QM with a natural probability interpretation. arXiv 2012, 1, 1-8, 10.48550/arXiv.1206.1237.
