Chaotic Image Encryption: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Vivi Li and Version 1 by Behrouz Zolfaghari.

Chaos is the characteristic of a system whose current state is guaranteed to be highly sensitive to the previous state (spatial chaos), the initial conditions (temporal chaos), or both (spatio-temporal chaos). Such a sensitivity makes the output or the behavior of a chaotic system difficult to predict. Chaos theory justifies and formulates the apparent disorder of chaotic systems on the basis of orderly patterns, structured feedback loops, iterative repetitions, self-organization, self-similarity, fractals, etc. Chaotic maps, attractors, and sequences all refer to the mathematical structures used for this formulation. Chaotic systems, maps, attractors, and sequences have been of great interest to the research community in recent years [12,13]. They have been used for security purposes in a broad variety of applications ranging from smart grids [14] to communication systems [15]. Especially, chaotic encryption has been used for encrypting a variety of content types in addition to images [1,2].

  • image encryption
  • chaos
  • chaotic encryption
  • chaotic image encryption

1. Introduction

Figure 1 illustrates how image encryption converges with chaos theory at chaotic image encryption.
Asi 05 00057 g001 550
Figure 1.
 Chaotic Image Encryption: The Convergence Point of Image Encryption and Chaos Theory.

2. StChate-of-the-Arotic Image Encryption​

Research on chaotic image encryption is going on in three aspects; chaos, image, and encryption. These aspects are shown in Figure 2. The state-of-the-art in each of the mentioned aspects is reviewed below.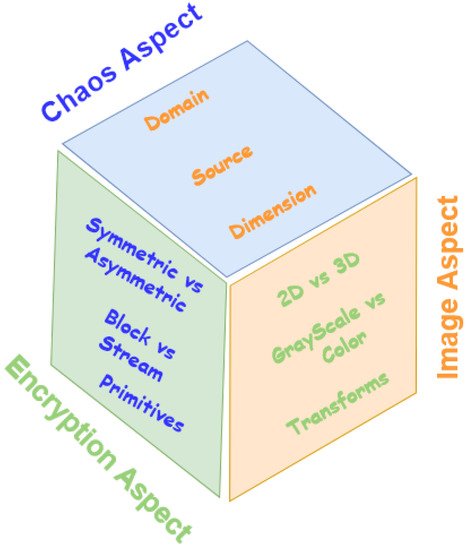
Asi 05 00057 g002 550
Figure 2.
 Aspects of Research on Chaotic Image Encryption.
As seen in Figure 2, the chaos aspect is about chaos domains, sources, and dimensions. The image aspect studies 2D versus 3D images, gray-scale versus color images, and image transforms. Moreover, the encryption aspect is related to symmetric versus asymmetric encryption, block ciphers versus stream ciphers, and cryptographic primitives. The research works reviewed in this section are categorized according to these aspects.

2.1. State-of-the-Art in Chaos Aspect

Researchers focusing on the chaos aspect have tried different chaos domains, sources, and dimensions. These concepts are studied below along with related research works.

2.1.1. Chaos Domains

Chaos is studied in three domains; space domain (spatial chaos), time domain (temporal chaos), and space–time domain (spatio-temporal chaos). All of these domains play roles in chaotic image encryption. These roles are reviewed in the following.

Spatial Chaos

Spatial chaotic systems and maps are functions that only depend on an input value to determine the state. They have many uses in image encryption; for example, ShuTang et al. [35][1] utilized a 2D spatial map in a novel image encryption algorithm that exhibits strong security after applying key sensitivity tests, adjacent pixel correlation analysis, keyspace analysis, and testing against various attacks. Other works in the spatial domain include that performed by Faragallah et al. [36][2], where they compiled a report investigating the effectiveness of several chaotic maps in the spatial domain, those being the Arnold cat map, baker map, and logistic map. The report describes the analysis of the maps’ effectiveness in a novel encryption scheme using visual, entropy, histogram, encryption quality, differential, Known Plain Text (KPA), and Chosen Plain Text (CPT) analysis.

Temporal Chaos

A temporal system only depends on a time index and the state of the system at the previous index to determine the current state. Once such pure temporal chaos system, referred to as a “super-chaotic” map, was utilized by Wang et al. [37][3] in a proposed image encryption algorithm that exhibited strong security properties such as a large keyspace, high key sensitivity, and statistical analysis resistance.

Spatiotemporal Chaos

A spatiotemporal chaotic system depends on both the spatial domain (input) and the time index. Encryption schemes using spatiotemporal chaos have been proposed by Xin et al. [38][4] and Luo et al. [39][5] where the chaos systems were paired with the Discrete Cosine Transform (DCT). The former additionally employs the Propagating Cipher-Block Chaining (PCBC) mode to achieve the image encryption, which contrasts with the work performed by He et al. [40][6], where the basic Cipher Block Chaining (CBC) mode was opted for instead. All three algorithms exhibit strong security when analyzed using encryption analysis methods. Another work in the spatiotemporal domain was performed by Xingyuan et al. [41][7]. In their paper, they proposed a novel spatiotemporal chaos model called the Logistic-Dynamic Coupled Logistic Map Lattice (LDCML). Analysis of the proposed map demonstrated strong chaotic properties, and when applied to image encryption, the further experimental analysis showed high levels of effectiveness.

2.1.2. Chaos Sources

Chaos can be created using mathematical or physical sources. In the following, wresearchers discuss the role of both types in the state-of-the-art of chaotic image encryption.

Mathematical Sources

Well-known mathematical chaos sources commonly used for image encryption purposes are studied below:
  • Chaotic systems and maps
    These are functions originally designed for creating chaos. Chaotic systems and maps play a critical role in chaotic image encryption. To mention a few, one may refer to the following:
  • Optical Chaos
    Our physical world can provide many forms of chaos, with just one example being light. In studies by Xie et al. [76][42] and Lui et al. [77][43], they found success in producing a chaotic base for image encryption algorithms using lasers. Extensive security testing of both algorithms showed them to be highly secure and feasible for practical use.
    –
    Fractional-order chaotic system
    Fractional calculus goes back more than 300 years, with modern studies focusing on systems such as the fractional-order Chen, Lorenz, and Liu systems
    Other studies have also been carried out, such as those by Li et al. [78][44]
    [
    42
    ][8]. A novel switching fractional-order chaos system was proposed by Hou [42][8] and utilizes controlling switches to switch between its sub-systems and achieve a strong chaos source for applying the exclusive Or (XOR) operation against the plaintext image.
    Another algorithm utilizing fractional-order systems was proposed by Wei [43][9], which opts to use a more standard third-order fractional system, as well as a novel Josephus scrambling algorithm and circular diffusion to achieve desirable encryption properties and resilience against common attacks.
    –
    Arnold cat map
    Arnold mapping is a well-know transposition chaotic map that, in the context of cryptography, was used by Ranimol and Gopakumar [44][10], as well as Zhang et al. [45][11] to provide a method of permutating and de-correlating adjacent pixels in their proposed encryption algorithms. Both algorithms were proven to exhibit a large keyspace with high key sensitivity and be capable of resisting common attacks such as brute force, entropy, CPT, and KPT.
    –
    Coupled map lattice
    A Coupled Map Lattice (CML) is a form of spatiotemporal chaos map efficient for random number stream generation. In one use case, Wu [46][12] proposed a novel implementation of the CML to create encryption streams dependent not only on initial values, but also on intermediate cipher images by using said ciphertexts to modify the CML parameters. This adds a layer of plaintext dependency, which aids in the defense against several attacks.
    –
    Lorenz map
    A Lorenz system is a type of differential equation that is highly susceptible to initial conditions. Jiang and Fu [47][13] proposed an image encryption procedure in which the key is composed of the three inputs to a 3D Lorenz system and utilizes the chaotic nature of said system to provide strong security.
    –
    Logistic map
    A logistic map is a relativity simplistic mathematical mapping function, which when influenced by particular control values, acts chaotically. An algorithm proposed by Sharma and Bhargava [48][14] utilizes a two-step interactive logistic map, where the next input is dependent on the previous two outputs, as a source of chaos. Similar work was performed by Li-Hong et al. [49][15], where they used a more standard logistic map and paired it with a hyper-chaos system to improve key generation effectiveness. Likewise, Mu and Lui [50][16] also found success utilizing the logistic map for key generation.
    –
    Tent map
    Wu et al. [51][17] proposed an image encryption algorithm using the CTM, and the rectangular transform was later analyzed by Zhu et al. [52][18] and improved upon to better protect against plaintext attacks such as CPT and KPT. The Chaotic Tent Map (CTM) is a mapping function that, when configured with control values in a particular range, behaves chaotically.
    –
    Lotka–Volterra
    A Lotka–Volterra chaotic system is a third-order differential equation in a similar family to other systems such as Lorenz, Rossler, Shua, and Chen. In a particular case study by Zahir et al. [53][19], an encryption procedure was proposed that utilizes the Lotka–Volterra chaotic system to aid in the creation of Substitution boxes (S-boxes) with strong confusion properties. The resulting S-boxes were found to satisfy the five criteria (bijective, non-linearity, strict avalanche, bit independence, input/output XOR distribution) required for acceptable use in cryptographic algorithms.
    –
    investigated the inefficiencies with single chaos systems and proposed a novel algorithm utilizing LSS and cascade chaos to improve upon said inefficiencies. Experimental analysis through simulation has proven the new algorithm to be highly resilient
    and Liu et al. [79][45]
    Henon map
    The Henon map was first discovered in 1978 and can be described as a 2D mapping function with two control parameters, which, when chosen strategically, enable the map to behave chaotically. Tresor et al.
    [
    54
    ]
    [
    20
    ]
    proposed an image encryption algorithm utilizing Henon maps for shuffling the pixels of the image and 4D Qi hyper-chaos to generate keys for encryption. Experimental analysis of the algorithm demonstrates strong cryptographic properties and resistance against common attacks.
    –
    Logistic-sine system
    A Logistic-Sine System (LSS) is a discrete combination of the logistic and sine maps, both of which exhibit chaotic behavior under particular initial conditions. Zeng and Chen
    [
    55
    ][21] referred to such a combination of the two maps as a compound chaotic map and utilized it in a novel encryption algorithm using XOR and modulus operations.
    Zhao et al. [56][22]
    In another study, Lu et al. [57][23] conducted cryptanalysis on an existing algorithm based on multiple S-boxes, but were able to break it using CPT attacks. A new algorithm was proposed to improve upon the old one and involved only a single S-box constructed utilizing LSS. Further cryptanalysis of the new algorithm showed improvement over the original and was also quite fast.
    Variants of LSS have also been employed in encryption algorithms, such as a 2D Logistic Modulated Sine Coupling Logistic (LSMCL) map proposed by Zhu et al. [58][24], a Logistic Sine Modulation Map (LSIMM) proposed by Zhang et al. [59][25], and a 2D Logistic Adjusted Sine Chaotic Map (LASCM) proposed by Balakrishnan and Mubarak [60][26]. In all cases, theoretical analysis and simulations determined the algorithms to be both secure and efficient.
    –
    Baker map
    The baker map is a bijective permutation function that operates on an MxM matrix by randomizing its cells according to a secret key and is well respected in the image encryption community. Elshamy et al. [61][27] utilized the baker map in an image encryption algorithm to improve upon a classic technique known as Double Random Phase Encoding (DRPE). The proposed algorithm uses the map to pre-process the image before applying DRPE, and experimental analysis showed significant increases in security as opposed to using DRPE alone.
    Another algorithm utilizing the baker map was proposed by Tong et al. [62][28], where high-dimensional dynamical multiple chaos was paired with the baker map to achieve a larger avalanche effect. Experimental results again showed significant increases in security when
    –
    Tinkerbell map
    Krishna [63][29] proposed an encryption algorithm utilizing Tinkerbell maps, a pair of chaotic functions, to inject strong pseudo-random numbers in multiple points during the encryption and decryption process. Differential and correlational analysis of the algorithm showed the proposed method to be highly efficient.
    –
    Cubic map
    A cubic map is a single-dimensional chaotic function that produces values on the interval [0, 1] and can be controlled by a single mapping parameter. Kavinmozhi et al. [64][30] proposed an encryption technique that employs a hybrid chaos source composed of the cubic and tent maps, as well as the Iterative Chaotic Map with Infinite Collapses (ICMICs). The resulting hybrid map is used with the XOR operation to achieve encryption, and an analysis of the algorithm showed that it is suitable for repeated use and is resilient against attacks.
    –
    Gingerbreadman map
    Savitri et al. [65][31] used the Gingerbreadman map, a 2D chaotic map, to generate encrypted keys for use with the well-known Cipher Block Chain (CBC) encryption algorithm. Using the map in this algorithm greatly improves CBC’s performance when applied to images, and a visual comparison demonstrated massive improvements.
    –
    Tangent map
    Moysis et al. [66][32] proposed a Random Number Generation (RNG) algorithm based on the usage of the mathematical hyperbolic tangent function. When the RNG algorithm was applied to image encryption, the resulting procedure demonstrated strong cryptography
    –
    Multiple maps
    Mixing multiple mapping functions in image encryption algorithms can serve multiple purposes. For example, Bisht et al. [67][33] employed a verity of different maps to achieve tasks such as more chaotic permutation, diffusion, and RNG. A similar technique employing various maps in different stages of the encryption procedure was also proposed by Wang et al. [68][34].
    Fu et al. [69][35] proposed a novel keystream generation technique utilizing multiple chaotic maps that incorporates the plaintext itself into the stream. The algorithm was motivated by the need to defend against CPT and KPT attacks, and an analysis of the algorithm showed it is effective in achieving its goal.
    In terms of areas of application, stronger algorithms enforced by the use of multiple chaotic maps are important in numerous fields. For example, Choi et al. [70][36] proposed an algorithm using multiple maps for encrypting colored medical images, which can be seen as unique in their size and sensitivity. Experimental and statistical analysis of the resulting procedure showed it is secure for use with healthcare images.
    , where optical chaos is utilized for encrypting and then transmitting images for storage in the cloud. Experimental results showed both procedures to be secure and safe for production use.
  • Other mathematical sources
    In addition to chaotic systems and maps, some researchers have used the following mathematical designs, which have not been originally defined for chaos creation:
    [
    83
    ]
    [
    49
    ] using a memristive chaotic system. The presented system demonstrates a unique property known as multistability, which further improves the chaoticness of the system. Again, security analysis showed the algorithm to possess strong cryptographic properties.
    –
    –
    Space-filling curves
    Fractal geometry has several intriguing properties, such as self-similarity, composition by iterative methods, and a complex structure. Zhang et al. [71][37] utilized Hilbert curves and H-fractals, types of self-filling curves, in a novel image encryption algorithm. This algorithm alternates the use of both curves to efficiently scramble the pixels of the image.
    –
    Memory cellular automata
    Cellular Automata (CA) can best be described as a grid of cells with a finite set of states and a transition function that governs how cells change state over time. Whereas a standard CA only depends on the generation t-1, Memory Cellular Automata (MCA) depend on more parameters. When the MCA’s rules are defined by chaotic maps, the structure becomes a powerful tool for image encryption. Several algorithms using various-order MCAs have been proposed, for example a 4D MCA by Aslam et al. [72][38], a 2D MCA by Hibibipour et al. [73][39], and an indefinite CA by Hibibipour et al.
  • Chaotic circuits
    –
    Chua circuit
    Some physical electronic circuits such as the Chua circuit can produce chaotic behavior. AlMutairi et al. [80][46] utilized the circuit as a key generator in their proposed image encryption algorithm. By contrast, Lin et al. [81][47] proposed a similar encryption model, but instead utilized a variant of the classic Chua circuit with a PWL memristor. In both cases, analysis showed the algorithms to exhibit strong security properties.
    –
    Memristive circuits
    A memristor is a form of electrical component that is capable of exhibiting chaotic behavior. Liu et al. [82][48] proposed an image encryption algorithm that utilizes 4D memristive hyper-chaos to create chaos matrices. Security analysis showed strong security and cryptographic properties.
    Another image encryption algorithm was proposed by Sun et al.
    [
    74
    ]
    [
    40].
    –
    Transcendental numbers
    In mathematics, a transcendental number has the characteristic that digits to the right of the decimal have no pattern [75][41]. Garcia et al. [75][41] proposed an image encryption algorithm that uses chaos and the transcendental number Pi, dubbed Chaotic Pi Ciphering (CPC). The algorithm uses Pi and a chaos source created using differential equations to generate cipher keys and substitution boxes.

Physical Sources

In addition to mathematical sources, chaos can be created using physical phenomena and used in chaotic image encryption:] proposed an image encryption algorithm utilizing the transform, which has some desirable attack resistances, for example against JPEG compression.

Linear Canonical Transform (LCT)

Li et al. [113][79] proposed an image encryption algorithm utilizing LCT that is both speedy in execution and also boasts a large keyspace to protect against brute-force attacks.

2.3. State-of-the-Art in the Encryption Aspect

The last aspect of chaotic image encryption is the encryption aspect, which is about symmetric versus asymmetric cryptography, block versus stream ciphers, and cryptographic primitives. The state-of-the-art in this aspect is studied below.

2.3.1. Symmetric versus Asymmetric Cryptography

Symmetric key encryption involves the use of the same key in both encryption and decryption and is common in many algorithms such as the Advanced Encryption Standard (AES). Ashtiyani et al. [114][80] proposed an image encryption algorithm for encrypting medical images using a chaotic variant of the Simplified Advanced Encryption Standard (S-AES). Asymmetric key encryption involves the use of different (but related) keys for encryption and decryption. Wu et al. [115][81] proposed an algorithm that utilizes a complex and irreversible function that causes the algorithm to exhibit asymmetric properties.

2.3.2. Block Cipher vs. Stream Cipher

Block and stream ciphers, although common with arbitrary binary encryption, typically fall short when encrypting images. However, when paired with sufficient chaos, they can be used effectively. Some block ciphers used in chaotic image encryption are studied below:
  • Blowflish
    Bora et al. [116][82] proposed a block cipher using the Blowfish algorithm and cross-chaos map. Cryptanalysis results showed strong security.
  • Ecliptic Curve Cryptography (ECC)
    Abbas et al. [117][83] proposed an Ecliptic-Curve (EC)-based algorithm that utilizes pixel-level parallelism for faster encryption speeds. A different proposal by Benssalah and Rhaskali et al. [118
    Physically Unclonable Functions (PUFs)
    True Random Number Generators (TRNGs), although very important in cryptography, are impossible to achieve in software. To counter this fact, Muhammad et al.
    [
    84
    ]
    [50] proposed an encryption algorithm using a hardware device, a form of physically unclonable function, to generate true random numbers. Through extensive experiments and analysis, the TRNG was successful in passing all tests required for safe use in cryptographic algorithms.

2.1.3. Chaos Dimension

The dimension of a chaos map refers to the number of functions (x(t), y(t), etc.) it is composed of. Many image encryption algorithms utilize chaotic functions of varying dimensions. Chaotic functions used in chaotic image encryption can be categorized as follows:
  • ]
  • [
    84] uses ECC combined with the Hill cipher and Arnold cat map to achieve a strong encryption algorithm targeted at medical images.
  • El-Gamal
    El-Gamal is a type of EC commonly utilized in cryptography. For example, Luo et al. [119][85] proposed a public-key-based image encryption algorithm utilizing the El-Gamal EC to address common issues with key management. In another proposal by Yousif et al. [118][84], El-Gamal was used to encrypt images that were first permutated using zigzag and spiral scanning.
  • Rijindal
    Dsouza and Sonawane [120][86] proposed a novel technique of using images as the key to encrypt/decrypt a directory in a file system. This technique employs both AES and Rijideal ciphers, and evaluation results demonstrated its effectiveness.
  • Rivest–Shamir–Adleman Cryptosystem (RSA)
    Nkapkop et al. [121][87] developed a novel asymmetric image encryption algorithm using RSA to solve the issue of key management. This algorithm uses the RSA key pairs to encrypt the initial values and parameters of the chaotic function so that the public key can encrypt images and only the private key can decrypt.
  • Data Encryption Standard (DES)
    Zhang et al. [122][88] proposed an image encryption algorithm utilizing the logistic chaos sequence for chaotic sequence generation and an improved DES algorithm for encryption. Simulation results demonstrated good security and speed, making it suitable for real-time use.
  • Novel block ciphers
    Gupta et al. [123][89] proposed a novel block cipher using two keys where the image is split into four blocks; each is encrypted n times, and finally, the keys are inverted and the blocks further encrypted m more times. Evaluation through standard tests demonstrated strong cryptographic properties, making the algorithm usable for real-time connections.
    Rani and Kumar [124][90] proposed a novel stream cipher using a modified RC4 algorithm. The algorithm converts the image into three vectors for each color channel and uses the modified RC4 stream algorithm to encrypt them. Another algorithm utilizing the RC4 stream cipher was proposed by Ginting and Dillak [125][91]. This algorithm uses the logistic map to generate a keystream for encryption. The algorithm is lossless, which was verified by comparing the hash values of the image before encryption and the image after encrypting, then decrypting.
  • Hybrid ciphers
    A hybrid approach utilizing both block and stream ciphers was proposed by Goumidi and Hachouf [126][92]. This algorithm splits the image into two sub-images and encrypts one using the block cipher and the other using the stream ciphers. The encrypted sub-images are then merged back together to form the final image. The use of two different types of ciphers greatly increases the complexity of the algorithm, leading to stronger cryptographic properties.
  • One-dimensional
    Work with one-dimensional chaos includes that by Wang and Lui [85][51], where the novel 1D Sine Chaotic System (1DSCS) was proposed. This system exhibits a large parameter interval as compared to the standard sine map it was built upon.
    Elghandour et al. [86][52] proposed an image encryption algorithm utilizing the 1D tent map. A similar algorithm also using the tent map was proposed by Tiwari et al. [87][53]. Extensive testing proved both algorithms to be effective at resisting common cryptographic attacks. The former paper also elaborated on the low chaotic range for the tent map and suggested that future work use a variant with a larger range such as the tent-sine map.
  • Two-dimensional
    An image encryption algorithm based on two-dimensional chaos was proposed by Yang and Tong [88][54]. This algorithm uses the 2D logistic chaotic system and a novel block image encryption procedure. Experimental results demonstrated the algorithm to have strong randomness, low pixel correlations, and high key sensitivity.
  • Three-dimensional
    Many image encryption algorithms utilize three-dimensional chaos. One such algorithm was proposed by Qian et al. [89][55], where they utilized the 3D logistic and cat maps. The novel usage of image reconstruction techniques also improved the effectiveness of the algorithm.
    In an algorithm proposed by Asl et al. [90][56], the 2D image was converted into three-dimensional space by creating three streams from the red, green, and blue channels of the image. The 3D modular chaotic map was used as the chaos source for encryption.
    Two other algorithms using three-dimensional chaos systems were proposed by Cao and Fu [91][57] and Xiu-chun and E-Nuo [92][58], respectively. In the former, the Rossler chaos system was used, whereas the latter study opted to use the Lorenz system.
  • Four-dimensional
    Huang et al. [93][59] proposed a novel four-dimensional chaos system based on concepts known as “shape synchronization” and “driver-response”. The complex mathematical underpinnings make the algorithm very difficult to break, and experimental tests in the application of image encryption showed promising results for its effectiveness.
  • Five-dimensional
    Zhu and Zhu [94][60] proposed a novel five-dimensional chaotic map composed of the 2D logistic map and 3D discrete Lorenz map. Experimental simulations of the system when applied to image encryption resulted in high scores in many common encryption strength tests.
  • Multiple dimensional
    Work related to mixing maps of varying dimensions in image encryption has also been performed. For example, Qui and Yan [95][61] proposed an image encryption algorithm using both the 1D logistic map and 3D Lorenz system. Experimental results demonstrated that the algorithm has strong security.
    Parida et al. [96][62] proposed a novel image encryption and transmission procedure based on Elliptic Curve Cryptography (ECC). Encryption is achieved using 3D and 4D Arnold cat maps as chaos sources, and the Elliptic Curve Diffie–Hellman (EDCH) key exchange algorithm is utilized to establish a shared key between parties. Digital signatures allow the algorithm to authenticate the encrypted message before decryption, and experimental results showed the method to be effective.

2.2. State-of-the-Art in the Image Aspect

The image aspect of chaotic image encryption is about 2D versus 3D, color versus gray-scale, and image transforms. In the following, wresearchers discuss each of these topics and show how they are dealt with in research works focusing on chaotic image encryption.

2.2.1. Two-Dimensional versus Three-Dimensional Image

Although 2D images are much more common, 3D images, which can be visualized as 3D meshes, do exist and possess the same encryption requirements as their two-dimensional counterparts. Due to this fact, 3D image encryption algorithms are much less common. However, one such algorithm was proposed by Xu et al. [97][63].

2.2.2. Gray-Scale versus Color Image

Several algorithms that focus specifically on gray-scale image encryption have been proposed such as one that interestingly utilizes the concept of water waves [98][64] and another that uses the integer wavelet transform [99][65]. If color image encryption is required, then gray-scale-specific algorithms will typically not suffice. Algorithms that encrypt color images employ a wide range of techniques such as matrix convolution [100][66] and 4D memristive hyper-chaos [82][48]. An approach for encrypting multiple colored images has also been proposed [101][67], as well as a unique procedure for encrypting and transmitting color images using audio signals [102][68].

2.2.3. Transforms

Image transforms are of critical importance in chaotic image encryption. Some of them are studied below.

Wavelet

The wavelet transform is a popular method of permutating the cells of a 2D matrix and can yield a significant increase in encryption effectiveness [103][69]. To fulfill the chaos requirement of good encryption, several chaos sources have been paired with the wavelet transform including an improved 3D cat map [104][70], a 1D logistic map [105][71], a 3D logistic map [106][72], the Arnold map [107,108][73][74], and a logistic sequence [108][74]. Other algorithms utilizing variations of the standard wavelet transform such as the Integer Wavelet Transform (IWT) have also been proposed [109][75].

Zigzag Transform

The zigzag transform is capable of rearranging the cells of a 2D matrix to heavily decrease the correlation between adjacent pixels, an important property when considering image encryption. Gao et al. [110][76] proposed an algorithm for image encryption utilizing a more complicated implementation of the transform that yields better security.

Cosine Transform

Zhang et al. [111][77] proposed an image encryption algorithm utilizing the Discrete Fraction Cosine Transform (DFrCT), which has additional benefits over the standard Discrete Cosine Transform (DCT) that make it more suitable for image encryption.

Contourlet Transform

The contourlet transform provides a method of decorrelating the cells of a 2D matrix and was designed to improve upon the shortcomings of the wavelet transform when dealing with natural images. Jiang et al. [112][78

2.3.3. Primitives

In the following, wresearchers examine the role of cryptographic primitives such as scrambling, bit shuffling, hashing, secret sharing, one-time key, permutation, substitution, confusion, and diffusion in chaotic image encryption.

Scrambling

Scrambling is the process of permutating the pixels (or even bits in a pixel) so that the new ordering is unrecognizable from the original. Various methods of scrambling have been employed including Latin rectangle [127][93], logistic chaotic [128][94], and spiral [129][95].

Bit Shuffling

Bit shuffling is another method of permutating the pixels of an image, specifically at the bit level. Krishnamoorthi et al. [130][96] proposed a method of bit shuffling in the spatial domain using a tent map.

Hashing

Hashing algorithms are special types of functions that take an input of any length and produce an output that is always the same length. The SHA algorithm specifically also has the added bonus of being highly input sensitive, that is to say, small changes in the input create a very different output. In the context of image encryption, one common use of hash algorithms is to generate the keystream. For example, Bhadke et al. [131][97] utilized SHA-256 and the Lorenz chaos attractor to generate strong key streams. Slimane et al. [132][98] also proposed an algorithm using the Lorenz chaos attractor and a hash algorithm, although they opted to use SHA-1 instead. In a paper by Lui [133][99], a novel encryption algorithm using SHA-3 and stenography was proposed. This algorithm embeds the hash of the plaintext image into the cipher image using stenography. This makes the algorithm very sensitive to the plain image, which in turn yields stronger security.

Permutation, Substitution, Confusion, and Diffusion

  • Permutation and diffusion
    Permutation is the process of rearranging elements in a structure, which, in the context of images, refers to scrambling the pixels. Abd-El-Hafiz et al. [134][100] performed an evaluation on three different permutation methods (discrete chaos, vectors, and Arnold cat map) and found that discrete performed the best.
    Diffusion is the process of ensuring there is no statistical significance to the resulting structure. In the context of images, this refers to scrambling the pixels of the image to eliminate the correlation between adjacent pixels. Ping et al. [135][101] proposed a novel digit-level permeation algorithm that additionally employs a high-speed diffusion algorithm. Evaluation results demonstrated high security and efficiency.
    Combining permutation with diffusion into the same stage of encryption aims to combat hackers who try to break each stage separately [136][102]. Liu et al. [137][103] proposed an algorithm to perform permutation and diffusion simultaneously. The algorithm additionally uses a Hopfield chaotic neural network to perform further diffusion, which gives the algorithm greater key sensitivity.
  • Confusion
    Confusion in encryption refers to the level of dependency elements of the cipher-text have with the key. As seen with permutation, confusion is often integrated with diffusion for the same reasons. For example, Run-he et al. [138][104] proposed an image encryption algorithm that achieves an integration of confusion and diffusion by XORing the plain image with chaotically generated offset matrices.
  • Substitution
    Substitution involves replacing an element with something else in a predictable and invertible manner. The substitution requirement is commonly implemented using S-boxes, which are matrices that define how each input maps to its substituted value.
    For image encryption, chaos-based S-boxes include those generated from the chaotic sine map [139][105] and the logistic map [140][106]. Wang and Zhang [141][107] also proposed an algorithm with multiple S-box substitutions, where the order of the boxes is determined by a random chaos sequence. Another algorithm proposed by Khan et al. [142][108] splits the image into four blocks and applies a different S-box to each block. These S-boxes each originate from a different encryption algorithm (AES, PQL, APL, and Shipjack). Another paper by Lidong et al. [143][109] proposes a dynamic encryption algorithm so that the cipher image is always different even if the same key and plain image are used.

One-Time Key

Rehman et al. [144][110] proposed an image encryption algorithm that uses a one-time-key to generate chaotic maps using the hash of the plaintext image. The algorithm employs a novel concept known as a rotor machine, and through simulation, the results showed that the algorithm possesses strong cryptographic properties.

Secret Sharing

Multiple Secret Sharing (MSS) in the context of image encryption is where k plaintext images are required to create k cipher-text images, and those same k cipher-text images are required to obtain even just one plaintext image [145][111]. Guo et al. [145][111] proposed an MSS algorithm for images that addresses common shortcomings.

References

  1. Liu, S.; Liu, S.; Sun, F.S. Spatial chaos-based image encryption design. Sci. China Ser. Phys. Mech. Astron. 2009, 52, 177–183.
  2. Faragallah, O.S.; Afifi, A.; El-Shafai, W.; El-Sayed, H.S.; Naeem, E.A.; Alzain, M.A.; Al-Amri, J.F.; Soh, B.; El-Samie, F.A. Investigation of chaotic image encryption in spatial and frft domains for cybersecurity applications. IEEE Access 2020, 8, 42491–42503.
  3. Wang, J.; Chen, G. Design of a chaos-based digitlal image encryption algorithm in time domain. In Proceedings of the IEEE International Conference on Computational Intelligence & Communication Technology, Ghaziabad, India, 13–14 February 2015.
  4. Ge, X.; Liu, F.; Lu, B.; Wang, W.; Chen, J. An image encryption algorithm based on spatiotemporal chaos in dct domain. In Proceedings of the 2nd IEEE International Conference on Information Management and Engineering, Chengdu, China, 16–18 April 2010.
  5. Luo, Y.; Du, M.; Liu, D. Jpeg image encryption algorithm based on spatiotemporal chaos. In Proceedings of the Fifth International Workshop on Chaos-fractals Theories and Applications, Dalian, China, 18–21 October 2012.
  6. He, B.; Zhang, F.; Luo, L.; Du, M.; Wang, Y. An image encryption algorithm based on spatiotemporal chaos. In Proceedings of the 2nd International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009.
  7. Wang, X.; Feng, L.; Wang, S.; Chuan, Z.; Zhang, Y. Spatiotemporal chaos in coupled logistic map lattice with dynamic coupling coefficient and its application in image encryption. IEEE Access 2018, 6, 2169–3536.
  8. Hou, J.; Xi, R.; Liu, P.; Liu, T. The switching fractional order chaotic system and its application to image encryption. IEEE/CAA J. Autom. Sin. 2017, 4, 381–388.
  9. Wei, J.; Zhang, M.; Tong, X. Image encryption algorithm based on fractional order chaotic system. In Proceedings of the IEEE 12th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 20–22 August 2021.
  10. George, R.T.; Gopakumar, K. Spatiotemporal chaos in globally coupled nca map lattices using 3-d arnold cat map for digital image encryption. In Proceedings of the First International Conference on Computational Systems and Communications (ICCSC), Trivandrum, India, 17–18 December 2014.
  11. Zhang, Y.; Xie, J.; Sun, P.; Huang, L. A new image encryption algorithm based on arnold and coupled chaos maps. In Proceedings of the International Conference on Computer and Communication Technologies in Agriculture Engineering, Chengdu, China, 12–13 June 2010.
  12. Wu, X. A novel chaos-based image encryption scheme using coupled map lattices. In Proceedings of the 10th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Shenyang, China, 23–25 July 2013.
  13. Jiang, H.Y.; Fu, C. An image encryption scheme based on lorenz chaos system. In Proceedings of the Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008.
  14. Sharma, M.; Bhargava, A. Chaos based image encryption using two step iterated logistic map. In Proceedings of the International Conference on Recent Advances and Innovations in Engineering (ICRAIE), Jaipur, India, 23–25 December 2016.
  15. Lei, L.-H.; Bai, F.-M.; Han, X.-H. New image encryption algorithm based on logistic map and hyper-chaos. In Proceedings of the International Conference on Computational and Information Sciences, Shiyang, China, 21–23 June 2013.
  16. Mu, Z.; Liu, H. Research on digital media image encryption algorithm based on logistic chaotic map. In Proceedings of the International Conference on Robots & Intelligent System (ICRIS), Sanya, China, 7–8 November 2020.
  17. Wu, X.; Zhu, B.; Hu, Y.; Ran, Y. A novel color image encryption scheme using rectangular transform-enhanced chaotic tent maps. IEEE Access 2017, 5, 6429–6436.
  18. Zhu, C.; Sun, K. Cryptanalyzing and improving a novel color image encryption algorithm using rt-enhanced chaotic tent maps. IEEE Access 2018, 6, 18759–18770.
  19. Muhammad, Z.M.Z.; Özkaynak, F. A cryptographic confusion primitive based on lotka–volterra chaotic system and its practical applications in image encryption. In Proceedings of the IEEE 15th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 25–29 February 2020.
  20. Tresor, L.O.; Sumbwanyambe, M. A selective image encryption scheme based on 2d dwt, henon map and 4d qi hyper-chaos. IEEE Access 2019, 7, 103463–103472.
  21. Zeng, H.; Chen, D. Image encryption algorithm based on logistic-sine compound chaos. In Proceedings of the International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery (CyberC), Chongqing, China, 29–30 October 2020.
  22. Zhao, F.; Li, C.; Liu, C.; Zhang, J. Image encryption algorithm based on sine-logistic cascade chaos. In Proceedings of the 5th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 19–22 April 2019.
  23. Lu, Q.; Zhu, C.; Deng, X. An efficient image encryption scheme based on the lss chaotic map and single S-box. IEEE Access 2020, 8, 25664–25678.
  24. Zhu, H.; Zhao, Y.; Song, Y. 2d logistic-modulated-sine-coupling-logistic chaotic map for image encryption. IEEE Access 2019, 7, 14081–14098.
  25. Zhang, H.; Zhu, J.; Zhao, S.; He, Q.; Zhong, X.; Liu, J. A new image encryption algorithm based on 2d-lsimm chaotic map. In Proceedings of the 12th International Conference on Advanced Computational Intelligence (ICACI), Dali, China, 14–16 August 2020.
  26. Balakrishnan, B.; Mubarak, D.M.N. An improved image encryption using 2d logistic adjusted sine chaotic map with shuffled index matrix. In Proceedings of the International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 19–20 February 2021.
  27. Elshamy, A.M.; Rashed, A.N.Z.; Mohamed, A.E.-N.A.; Faragalla, O.S.; Mu, Y.; Alshebeili, S.A.; El-Samie, F.E.A. Optical image encryption based on chaotic baker map and double random phase encoding. J. Light. Technol. 2013, 31, 2533–2539.
  28. Tong, X.; Liu, Y.; Zhang, M.; Wang, Z. A novel image encryption scheme based on dynamical multiple chaos and baker map. In Proceedings of the 11th International Symposium on Distributed Computing and Applications to Business, Engineering & Science, Guilin, China, 19–22 October 2012.
  29. Krishna, P.R.; Surya Teja, C.V.M.; Renuga, D.S.; Thanikaiselvan, V. A chaos based image encryption using tinkerbell map functions. In Proceedings of the Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 29–31 March 2018.
  30. Kavinmozhi, G.; Premkumar, R.; Anand, S.; Robinson, S. A hybrid chaos approach for image encryption using ctic map. In Proceedings of the International Conference on Current Trends towards Converging Technologies (ICCTCT), Coimbatore, India, 1–3 March 2018.
  31. Savitri, N.; Johan, A.W.S.B.; Islama, F.A.; Utaminingrum, F. Efficient technique image encryption with cipher block chaining and gingerbreadman map. In Proceedings of the International Conference on Sustainable Information Engineering and Technology (SIET), Lombok, Indonesia, 28–30 September 2019.
  32. Moysis, L.; Kafetzis, I.; Volos, C.; Tutueva, A.V.; Butusov, D. Application of a hyperbolic tangent chaotic map to random bit generation and image encryption. In Proceedings of the IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), St. Petersburg and Moscow, Russia, 26–29 January 2021.
  33. Bisht, A.; Jaroli, P.; Dua, M.; Dua, S. Symmetric multiple image encryption using multiple new one-dimensional chaotic functions and two-dimensional cat man. In Proceedings of the International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 11–12 July 2018.
  34. Wang, X.; Zhu, X.; Zhang, Y. An image encryption algorithm based on josephus traversing and mixed chaotic map. IEEE Access 2018, 6, 23733–23746.
  35. Fu, C.; Li, W.; Meng, Z.; Wang, T.; Li, P. A symmetric image encryption scheme using chaotic baker map and lorenz system. In Proceedings of the Ninth International Conference on Computational Intelligence and Security, Emeishan, China, 14–15 December 2013.
  36. Choi, U.S.; Cho, S.J.; Kang, S.W. Color image encryption algorithm for medical image by mixing chaotic maps. In Proceedings of the 12th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Porto, Portugal, 20–22 July 2020.
  37. Zhang, X.; Wang, L.; Zhou, Z.; Niu, Y. A chaos-based image encryption technique utilizing hilbert curves and h-fractals. IEEE Access 2019, 7, 74734–74746.
  38. Aslam, M.N.; Belazi, A.; Kharbech, S.; Talha, M.; Xiang, W. Fourth order mca and chaos-based image encryption scheme. IEEE Access 2019, 7, 66395–66409.
  39. Habibipour, M.; Maarefdoust, R.; Yaghobi, M.; Rahati, S. An image encryption system by 2d memorized cellular automata and chaos mapping. In Proceedings of the 6th International Conference on Digital Content, Multimedia Technology and Its Applications, Seoul, Korea, 16–18 August 2010.
  40. Habibipour, M.; Yaghobi, M.; Rahati-Q, S.; souzanchi k, Z. An image encryption system by indefinite cellular automata and chaos. In Proceedings of the 2nd International Conference on Signal Processing Systems, Dalian, China, 5–7 July 2010.
  41. García, V.M.S.; Ramírez, M.D.G.; Carapia, R.F.; Vega-Alvarado, E.; Escobar, E.R. A novel method for image encryption based on chaos and transcendental numbers. IEEE Access 2019, 7, 163729–163739.
  42. Xie, Y.; Li, J.; Kong, Z.; Zhang, Y.; Liao, X.; Liu, Y. Exploiting optics chaos for image encryption-then-transmission. J. Light. Technol. 2016, 34, 5101–5109.
  43. Liu, X.; Guo, R.; Li, M.; Wei, Z. Research on image encryption in secure communication system of space laser chaos keying. In Proceedings of the International Conference on Wireless Communications and Smart Grid (ICWCSG), Qingdao, China, 12–14 June 2020.
  44. Li, L.; Xie, Y.; Liu, Y.; Liu, B.; Ye, Y.; Song, T.; Zhang, Y.; Liu, Y. Exploiting optical chaos for color image encryption and secure resource sharing in cloud. IEEE Photonics J. 2019, 11, 1–11.
  45. Liu, B.; Xie, Y.; Zhang, Y.; Ye, Y.; Song, T.; Liao, X.; Liu, Y. Arm-embedded implementation of a novel color image encryption and transmission system based on optical chaos. IEEE Photonics J. 2020, 12, 1–12.
  46. AlMutairi, F.; Bonny, T. Image encryption based on chua chaotic oscillator. In Proceedings of the International Conference on Signal Processing and Information Security (ICSPIS), Dubai, United Arab Emirates, 25–26 November 2020.
  47. Lin, Z.H.; Wang, H.X. Image encryption based on chaos with pwl memristor in chua’s circuit. In Proceedings of the International Conference on Communications, Circuits and Systems, Milpitas, CA, USA, 23–25 July 2009.
  48. Liu, Z.; Wu, C.; Wang, J.; Hu, Y. A color image encryption using dynamic dna and 4-d memristive hyper-chaos. IEEE Access 2019, 7, 78367–78378.
  49. Sun, J.; Li, C.; Lu, T.; Akgul, A.; Min, F. A memristive chaotic system with hypermultistability and its application in image encryption. IEEE Access 2020, 8, 139289–139298.
  50. Muhammad, A.S.; Özkaynak, F. Siea: Secure image encryption algorithm based on chaotic systems optimization algorithms and pufs. Symmetry 2021, 13, 824.
  51. Wang, X.; Liu, P. A new image encryption scheme based on a novel one-dimensional chaotic system. IEEE Access 2020, 8, 174463–174479.
  52. Elghandour, A.N.; Salah, A.M.; Elmasry, Y.A.; Karawia, A.A. An image encryption algorithm based on bisection method and one-dimensional piecewise chaotic map. IEEE Access 2021, 9, 43411–43421.
  53. Tiwari, H.; Satish, K.N.; Harshitha, R.; Shilpa, N.; Rakshatha, S.; Archana, K.N. Ensuring confidentiality in bsn with 1-d chaos based image encryption scheme. In Proceedings of the International Conference on Advances in Computing, Communication Control and Networking (ICACCCN), Greater Noida, India, 12–13 October 2018.
  54. Yang, S.; Tong, X. A block image encryption algorithm based on 2d chaotic system. In Proceedings of the IEEE 12th International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 20–22 August 2021.
  55. Qian, X.; Yang, Q.; Li, Q.; Liu, Q.; Wu, Y.; Wang, W. A novel color image encryption algorithm based on three-dimensional chaotic maps and reconstruction techniques. IEEE Access 2021, 9, 61334–61345.
  56. Asl, A.M.; Broumandnia, A.; Mirabedini, S.J. Scale invariant digital color image encryption using a 3d modular chaotic map. IEEE Access 2021, 9, 102433–102449.
  57. Cao, Y.y.; Fu, C. An image encryption scheme based on high dimension chaos system. In Proceedings of the International Conference on Intelligent Computation Technology and Automation (ICICTA), Changsha, China, 20–22 October 2008.
  58. Mu, X.; E-Nuo, S. A new color image encryption algorithm based on 3d lorenz chaos sequences. In Proceedings of the First International Conference on Pervasive Computing, Signal Processing and Applications, Harbin, China, 17–19 September 2010.
  59. Huang, Y.; Huang, L.; Wang, Y.; Peng, Y.; Yu, F. Shape synchronization in driver-response of 4-d chaotic system and its application in image encryption. IEEE Access 2020, 8, 135308–135319.
  60. Zhu, S.; Zhu, C. Plaintext-related image encryption algorithm based on block structure and five-dimensional chaotic map. IEEE Access 2019, 7, 147106–147118.
  61. Qiu, W.C.; Yan, S.J. An image encryption algorithm based on the combination of low-dimensional chaos and high-dimensional chaos. In Proceedings of the 3rd International Conference on Electronic Information Technology and Computer Engineering (EITCE), Xiamen, China, 18–20 October 2019.
  62. Parida, P.; Pradhan, C.; Gao, X.; Roy, D.S.; Barik, R.K. Image encryption and authentication with elliptic curve cryptography and multidimensional chaotic maps. IEEE Access 2021, 9, 76191–76204.
  63. Xu, J.; Zhao, C.; Mou, J. A 3d image encryption algorithm based on the chaotic system and the image segmentation. IEEE Access 2020, 8, 145995–146005.
  64. Firdous, A.; Rehman, A.U.; Missen, M.M.S. A gray image encryption technique using the concept of water waves, chaos and hash function. IEEE Access 2021, 9, 11675–11693.
  65. Ravichandran, D.; Balasubramanian, V.; Fathima, S.; Banu, A.; Anushiadevi; Amirtharajan, R. Chaos and iwt blended image encryption for grey scale image security. In Proceedings of the International Conference on Vision Towards Emerging Trends in Communication and Networking (ViTECoN), Vellore, India, 30–31 March 2019.
  66. Hu, X.; Wei, L.; Chen, W.; Chen, Q.; Guo, Y. Color image encryption algorithm based on dynamic chaos and matrix convolution. IEEE Access 2020, 8, 12452–12466.
  67. Sun, Y.J.; Zhang, H.; Wang, C.P.; Li, Z.Y.; Wang, X.Y. Networked chaotic map model and its applications in color multiple image encryption. IEEE Photonics J. 2020, 12, 1–18.
  68. Yin, P.; Min, L. A color image encryption algorithm based generalized chaos synchronization for bidirectional discrete systems for audio signal communication. In Proceedings of the International Conference on Intelligent Control and Information Processing, Dalian, China, 13–15 August 2010.
  69. Wang, J. Image encryption algorithm based on 2-d wavelet transform and chaos sequences. In Proceedings of the International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 11–13 December 2009.
  70. Zhang, Q.; Shen, M.; Li, B.; Fang, R. Chaos-based color image encryption scheme in the wavelet domain. In Proceedings of the 7th International Congress on Image and Signal Processing, Dalian, China, 14–16 October 2014.
  71. Wang, Q.; Ding, Q.; Zhang, Z.; Ding, L. Digital image encryption research based on dwt and chaos. In Proceedings of the Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008.
  72. Zhang, S.; Cai, R.; Jiang, Y.; Guo, S. An image encryption algorithm based on multiple chaos and wavelet transform. In Proceedings of the 2nd International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009.
  73. Macovei, C.; Răducanu, M.; Datcu, O. Image encryption algorithm using wavelet packets and multiple chaotic maps. In Proceedings of the International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 5–6 November 2020.
  74. Li, X.; Zhang, Y. Digital image encryption and decryption algorithm based on wavelet transform and chaos system. In Proceedings of the IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 3–5 October 2016.
  75. Karmakar, J.; Mandal, M.K. Chaos-based image encryption using integer wavelet transform. In Proceedings of the 7th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 27–28 February 2020.
  76. Gao, H.; Wang, X. Chaotic image encryption algorithm based on zigzag transform with bidirectional crossover from random position. IEEE Access 2021, 9, 105627–105640.
  77. Zhang, L.; Wu, J.; Zhou, N. Image encryption with discrete fractional cosine transform and chaos. In Proceedings of the Fifth International Conference on Information Assurance and Security, Xi’an, China, 18–20 August 2009.
  78. Jiang, A.; Yu, J.; Cang, X. Image encryption algorithm based on chaos and contourlet transform. In Proceedings of the First International Conference on Pervasive Computing, Signal Processing and Applications, Harbin, China, 17–19 September 2010.
  79. Li, X.M.; Dai, L. Reality-preserving image encryption assosiated with the chaos and the lct. In Proceedings of the 3rd International Congress on Image and Signal Processing, Yantai, China, 16–18 October 2010.
  80. Ashtiyani, M.; Birgani, P.M.; Hosseini, H.M. Chaos-based medical image encryption using symmetric cryptography. In Proceedings of the 3rd International Conference on Information and Communication Technologies: From Theory to Applications, Damascus, Syria, 7–11 April 2008.
  81. Wu, Z.; Zhang, X.; Zhong, X. Generalized chaos synchronization circuit simulation and asymmetric image encryption. IEEE Access 2019, 7, 37989–38008.
  82. Bora, S.; Sen, P.; Pradhan, C. Novel color image encryption technique using blowfish and cross chaos map. In Proceedings of the International Conference on Communications and Signal Processing (ICCSP), Melmaruvathur, India, 2–4 April 2015.
  83. Abbas, A.M.; Alharbi, A.A.; Ibrahim, S. A novel parallelizable chaotic image encryption scheme based on elliptic curves. IEEE Access 2021, 9, 54978–54991.
  84. Yousif, S.F.; Abboud, A.J.; Radhi, H.Y. Robust image encryption with scanning technology, the el-gamal algorithm and chaos theory. IEEE Access 2020, 8, 155184–155209.
  85. Luo, Y.; Ouyang, X.; Liu, J.; Cao, L. An image encryption method based on elliptic curve elgamal encryption and chaotic systems. IEEE Access 2019, 7, 38507–38522.
  86. Dsouza, C.A.; Sonawane, K. Securing folder directory using image encryption by chaos and rijndael algorithm. In Proceedings of the International Conference on Communication information and Computing Technology (ICCICT), Mumbai, India, 25–27 June 2021.
  87. Nkapkop, J.D.D.; Effa, J.Y.; Toma, A.; Cociota, F.; Borda, M. Chaos-based image encryption using the rsa keys management for an efficient web communication. In Proceedings of the 12th IEEE International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 27–28 October 2016.
  88. Zhang, Y.; Liu, W.; Cao, S.; Zhai, Z.; Nie, X.; Dai, W. Digital image encryption algorithm based on chaos and improved des. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009.
  89. Gupta, K.; Gupta, R.; Agrawal, R.; Khan, S. An ethical approach of block based image encryption using chaotic map. Int. J. Secur. Appl. 2015, 9, 105–122.
  90. Rani, M.; Kumar, S. A novel and efficient approach to encrypt images using chaotic logistic map and stream cipher. In Proceedings of the International Conference on Green Computing and Internet of Things (ICGCIoT), Greater Noida, India, 8–10 October 2015.
  91. Ginting, R.U.; Dillak, R.Y. Digital color image encryption using rc4 stream cipher and chaotic logistic map. In Proceedings of the International Conference on Information Technology and Electrical Engineering (ICITEE), Yogyakarta, Indonesia, 7–8 October 2013.
  92. Goumidi, D.E.; Hachouf, F. Hybrid chaos-based image encryption approach using block and stream ciphers. In Proceedings of the 8th International Workshop on Systems, Signal Processing and Their Applications (WoSSPA), Algiers, Algeria, 12–15 May 2013.
  93. Chapaneri, S.; Chapaneri, R. Chaos based image encryption using latin rectangle scrambling. In Proceedings of the Annual IEEE India Conference (INDICON), Pune, India, 11–13 December 2014.
  94. Qu, J. Image encryption algorithm based on logistic chaotic scrambling system. In Proceedings of the IEEE 3rd International Conference on Information Systems and Computer Aided Education (ICISCAE), Dalian, China, 11–13 September 2020.
  95. Zhang, P.; Chen, M.; Zhang, J. Image encryption algorithm of hyper-chaotic system based on spiral scrambling. In Proceedings of the IEEE International Symposium on Product Compliance Engineering-Asia (ISPCE-CN), Chongqing, China, 6–8 November 2020.
  96. Krishnamoorthi, R.; Murali, P. Chaos based image encryption with orthogonal polynomials model and bit shuffling. In Proceedings of the International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 20–21 February 2014.
  97. Bhadke, A.A.; Kannaiyan, S.; Kamble, V. Symmetric chaos-based image encryption technique on image bit-planes using sha-256. In Proceedings of the Twenty Fourth National Conference on Communications (NCC), Hyderabad, India, 25–28 February 2018.
  98. Slimane, N.B.; Bouallegue, K.; Machhout, M. A novel image encryption scheme using chaos, hyper-chaos systems and the secure hash algorithm sha-1. In Proceedings of the International Conference on Control, Automation and Diagnosis (ICCAD), Hammamet, Tunisia, 19–21 January 2017.
  99. Liu, J. A novel sensitive chaotic image encryption algorithm based on sha-3 and steganography. In Proceedings of the IEEE 3rd International Conference of Safe Production and Informatization (IICSPI), Chongqing City, China, 28–30 November 2020.
  100. Abd-El-Hafiz, S.K.; AbdElHaleem, S.H.; Radwan, A.G. Permutation techniques based on discrete chaos and their utilization in image encryption. In Proceedings of the 13th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Mai, Thailand, 28 June–1 July 2016.
  101. Ping, P.; Fan, J.; Mao, Y.; Xu, F.; Gao, J. A chaos based image encryption scheme using digit-level permutation and block diffusion. IEEE Access 2018, 6, 59108–59130.
  102. Liu, L.; Lei, Y.; Wang, D. A fast chaotic image encryption scheme with simultaneous permutation-diffusion operation. IEEE Access 2020, 8, 27361–27374.
  103. Liu, L.; Zhang, L.; Jiang, D.; Guan, Y.; Zhang, Z. A simultaneous scrambling and diffusion color image encryption algorithm based on hopfield chaotic neural network. IEEE Access 2021, 7, 185796–185810.
  104. Koduru, S.C.; Chandrasekaran, V. Integrated confusion-diffusion mechanisms for chaos based image encryption. In Proceedings of the IEEE 8th International Conference on Computer and Information Technology Workshops, Sydney, NSW, Australia, 8–11 July 2008.
  105. Rehman, M.U.; Shafique, A.; Khalid, S.; Hussain, I. Dynamic substitution and confusion-diffusion-based noise-resistive image encryption using multiple chaotic maps. IEEE Access 2021, 9, 52277–52291.
  106. Hassan, J.M.; Kadhim, F.A. New S-box transformation based on chaotic system for image encryption. In Proceedings of the 3rd International Conference on Engineering Technology and Its Applications (IICETA), Najaf, Iraq, 6–7 September 2020.
  107. Wang, D.; Zhang, Y. Image encryption algorithm based on S-boxes substitution and chaos random sequence. In Proceedings of the International Conference on Computer Modeling and Simulation, Macau, China, 20–22 February 2009.
  108. Khan, J.S.; Rehman, A.U.; Ahmad, J.; Habib, Z. A new chaos-based secure image encryption scheme using multiple substitution boxes. In Proceedings of the Conference on Information Assurance and Cyber Security (CIACS), Rawalpindi, Pakistan, 18 December 2015.
  109. Lidong, L.; Jiang, D.; Wang, X.; Zhang, L.; Rong, X. A dynamic triple-image encryption scheme based on chaos, S-box and image compressing. IEEE Access 2020, 8, 210382–210399.
  110. Rehman, A.U.; Firdous, A.; Iqbal, S.; Abbas, Z.; Shahid, M.M.A.; Wang, H.; Ullah, F. A color image encryption algorithm based on one time key, chaos theory, and concept of rotor machine. IEEE Access 2020, 8, 172275–172295.
  111. Guo, J.; Riyono, D.; Prasetyo, H. Improved beta chaotic image encryption for multiple secret sharing. IEEE Access 2018, 6, 46297–46321.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback