Map Projections Classification: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Rita Xu and Version 1 by Miljenko Lapaine.

Many books, textbooks and papers have been published in which the classification of map projections is based on auxiliary (developable) surfaces and projections are divided into conic, cylindrical and azimuthal projections.

  • map projections
  • developable surfaces
  • classification

1. Background

So far, many books and textbooks of general, thematic and even mathematical cartography have been published, as well as articles in journals, in which one of the classifications of map projections is based on auxiliary (developable) surfaces and projections are divided into conic, cylindrical and azimuthal projections. This classification is illustrated by images in which the surface of a cone and the surface of a cylinder or a plane touch or intersect the Earth’s sphere (Figure 1).
Geographies 02 00019 g001
Figure 1. The three developable projection surfaces: cylinder, cone and plane. (Only half of the cylinder and cone are shown.) By permission of Charles Preppernau, the author of the image.

2. History

  • The authors of the oldest known cylindrical and conic projections did not define their projections using indirect, developable surfaces. For example, Mercator, in the 16th century, did not use a cylindrical surface to define the projection now called Mercator’s cylindrical projection, or Lambert, in the 18th century, did not use a conical surface to define the projection now called Lambert’s conformal conic projection. On the contrary, after deriving the equations of that projection, Lambert [13][1] mentioned that the map made in that projection could be folded into a cone.
  • It seems that developable surfaces related to map projections appear for the first time in the second half of the 19th century. D’Avezac-Macaya [4][2] referred to “les projections perspectives, les developements de surfaces osculatrices ou pénétrantes”, that is, tangent or secant surfaces, specifically “les développements cylindriques” and “cóniques”, and the catch-all “les systèmes conventionneles”. Snyder [3] did not find any earlier cartographic references to developable surfaces. Let uresearchers mention the famous older authors who dealt with map projections, not to mention developable surfaces: Lambert [13][1], Euler [14][4], Lagrange [15][5], Gauss [16][6] and Tissot [17][7].

3. Conceptuality

  • One of the most common classifications, and the one principally used by Snyder [3], is based on association, at least conceptually, to a developable surface.
  • Map projections are mappings of a curved surface, most often a sphere or ellipsoid, into a plane. The introduction of developable surfaces as intermediate surfaces and the interpretation according to which a sphere or ellipsoid is first mapped to such a surface which then develops into a plane is a fabrication that generally does not correspond to reality. It is usually justified by the term conceptual [2][8] and explained by the claim that map projections are easier to interpret in this way.
  • “The reference globe and developable surfaces are conceptual aids that help illustrate the projection process, but they are not used to create projections today. Rather, the field of mathematics is utilized to create projections, and so it is important to understand some of the basic mathematical manipulations used to project the Earth onto a map.” [9]. The first part of the first sentence is questionable because developable surfaces are not used in the projection process, in general. The rest of the quotation wresearchers fully accept. As everybody can see, there are no developable surfaces in the whole chapter 8.3 of the cited book.
  • “The classification of projections according to developable surfaces (cylinder, cone, and plane) is useful for the comprehension of selecting projections and their parameters. However, while developable surfaces are a useful conceptual tool, it needs to be emphasized that most map projections cannot be constructed geometrically but are instead defined mathematically” [18][10]. It remains unclear why Šavrič et al. [18][10] mentioned the classification of map projections using developable surfaces when they are not used in their Projection Wizard.
  • “While the concept of developable surfaces provides a nice way to visualize the basics of map projections, as stated before, the transformation is really driven by mathematical equations” [10][11]. The basics of map projections are not connected to developable surfaces at all.

4. Prior Warning

  • This approach to the classification of map projections is common. Map projections are typically classified according to the geometric surface from which they are derived: cylinder, cone or plane. However, such an approach is only correct at first glance. In fact, the opposite is true. Cylindrical projections are not called so because of the mapping on a cylindrical surface but because the map made in such a projection can be bent into a cylinder. Similarly, conic projections are not called so because of mapping to a conical surface but because a map made in a conic projection can be bent into a cone. More than 100 years ago, in a paper on map projections, Close and Clarke [19][12] wrote: “Conical projections are those in which the parallels are represented by concentric circles and the meridians by equally spaced radii. There is no necessary connexion between a conical projection and any touching or secant cone. The name conical is given to the group embraced by the above definition, because as is obvious, a projection so drawn can be round to form a cone.” In a well-known paper on the nomenclature and classification of map projections, Lee [20][13] explained: “Cylindric: projections in which the meridians are represented as a system of equidistant parallel straight lines, and the parallels by a system of parallel straight lines at right angles to the meridians.
    • Conic: projections in which the meridians are represented as...
    • Azimuthal: projections in which the meridians are represented as...
No reference has been made in the above definitions to cylinders, cones or planes. The projections are termed cylindric or conic because they can be regarded as developed on a cylinder or cone, as the case may be, but it is as well to dispense with picturing cylinders and cones, since they have given rise to much misunderstanding.”

5. Isometry

  • Authors who nowadays describe map projections in great detail with the help of developable surfaces may not even be aware of the fact that, in this way, they introduce double mappings into the theory of map projections. First, the Earth’s sphere is mapped to the auxiliary developable surface, and then it is transformed in some way, e.g., by development, into a map in the plane. Double mappings have their role in the theory of map projections in some special cases, not in general. One should know that developing into a plane is isometry, i.e., such a mapping that preserves distances.
  • The use of development surfaces in the definition of map projection is justified only for a small number of projections, projections in which the mapping is real and not conceptual to the corresponding developable surface. Namely, in addition to cylindrical and conic projections, there are many others, such as azimuthal, pseudocylindrical, pseudoconic, conditional, etc., which cannot be interpreted by mapping to a cylinder or cone surface. There are some attempts in that direction. For example, it is said that a pseudocylindrical projection is a mapping to a pseudocylinder but without saying what a pseudocylinder is [7][14]. Or that such a projection is interpreted as a mapping to an oval surface, without noticing that it is not a developable surface [8][15].
  • In the context of the classification of projections into conical, cylindrical and azimuthal/plane, it is unnatural to use a plane as a developable surface. Namely, developing is isometry, and thus wresearchers see no purpose in developing plane into plane.
  • Developing the auxiliary surface into a plane (Figure 2) preserves distances (isometry). This would then mean that the two selected parallels as standard parallels in all normal aspect projections are mapped to parallels that are at the same distance from each other. Is that possible? Of course not.
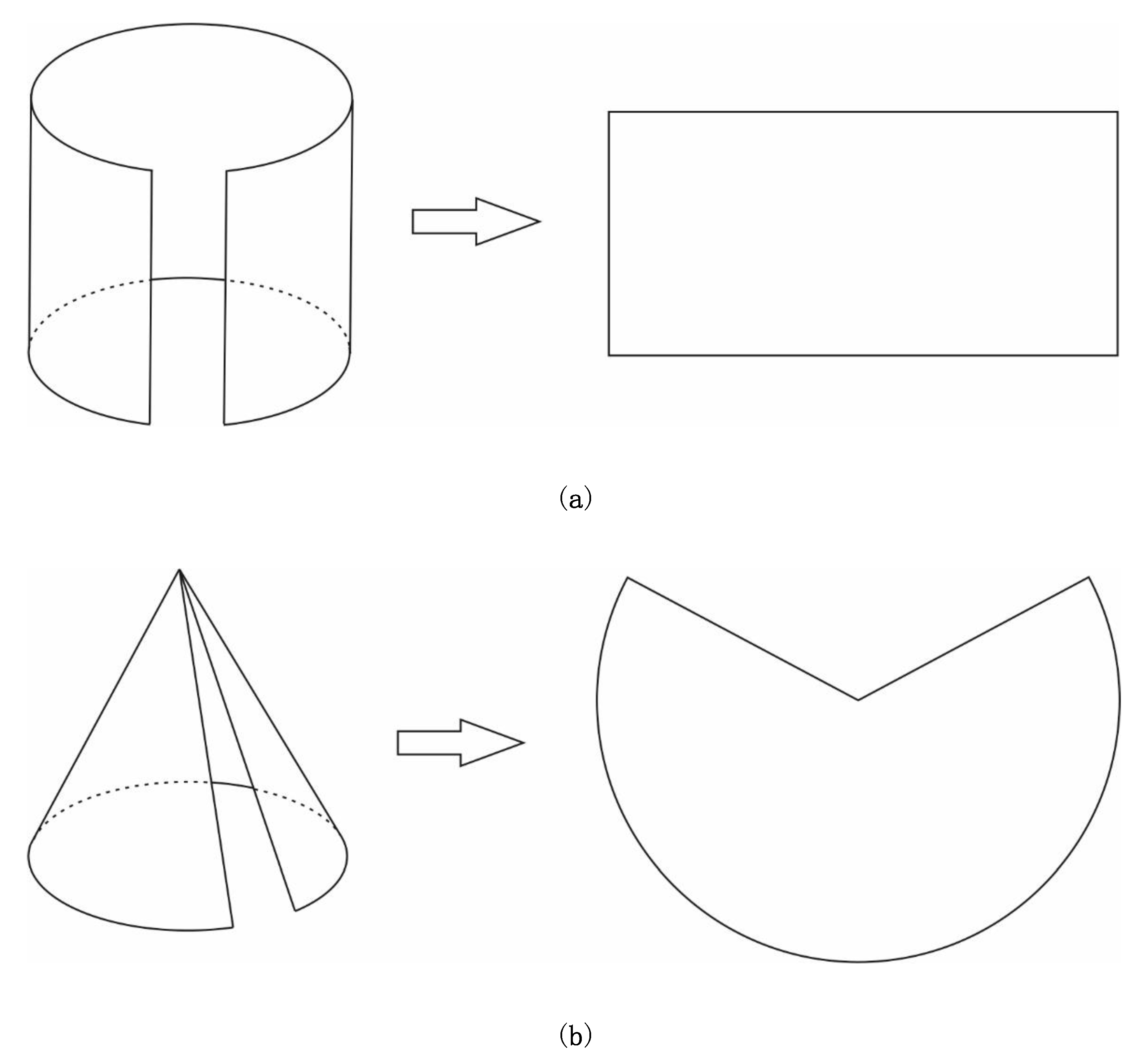
Geographies 02 00019 g002
Figure 2. (a) Cylindrical surface cut from base to base and development of the cylindrical surface. (b) Conical surface cut from base to apex and development of the conical surface.

6. Standard vs. Secant Parallels

  • Authors who perceive map projections as mappings with the help of an auxiliary surface regularly distinguish the case of touching and cutting. For them, as a rule, the cross-sectional curve is also a curve without deformations. They take that fact for granted, without proof. However, it has been shown that standard parallels and secant parallels are two different concepts and that they generally do not coincide
  • [
  • ,
  • 22,23][16][17][18].
  • “Where the ellipsoid and the map projection surface touch, in this case, intersect, there is no distortion. However, between the standard lines the map is under the ellipsoid and outside of them the map is above it.” [5,6][19][20]. From this quote, it is clear that van Sickle did not distinguish between secant and standard parallels.
  • The use of developable surfaces leads to secant projections, i.e., mappings on the auxiliary developable surface that intersects the mapped surface and thence the conclusion that azimuthal projections can have at most one standard parallel and conic at most two. This is wrong because there are azimuthal and conic projections with several standard parallels [24,[2125]][22].
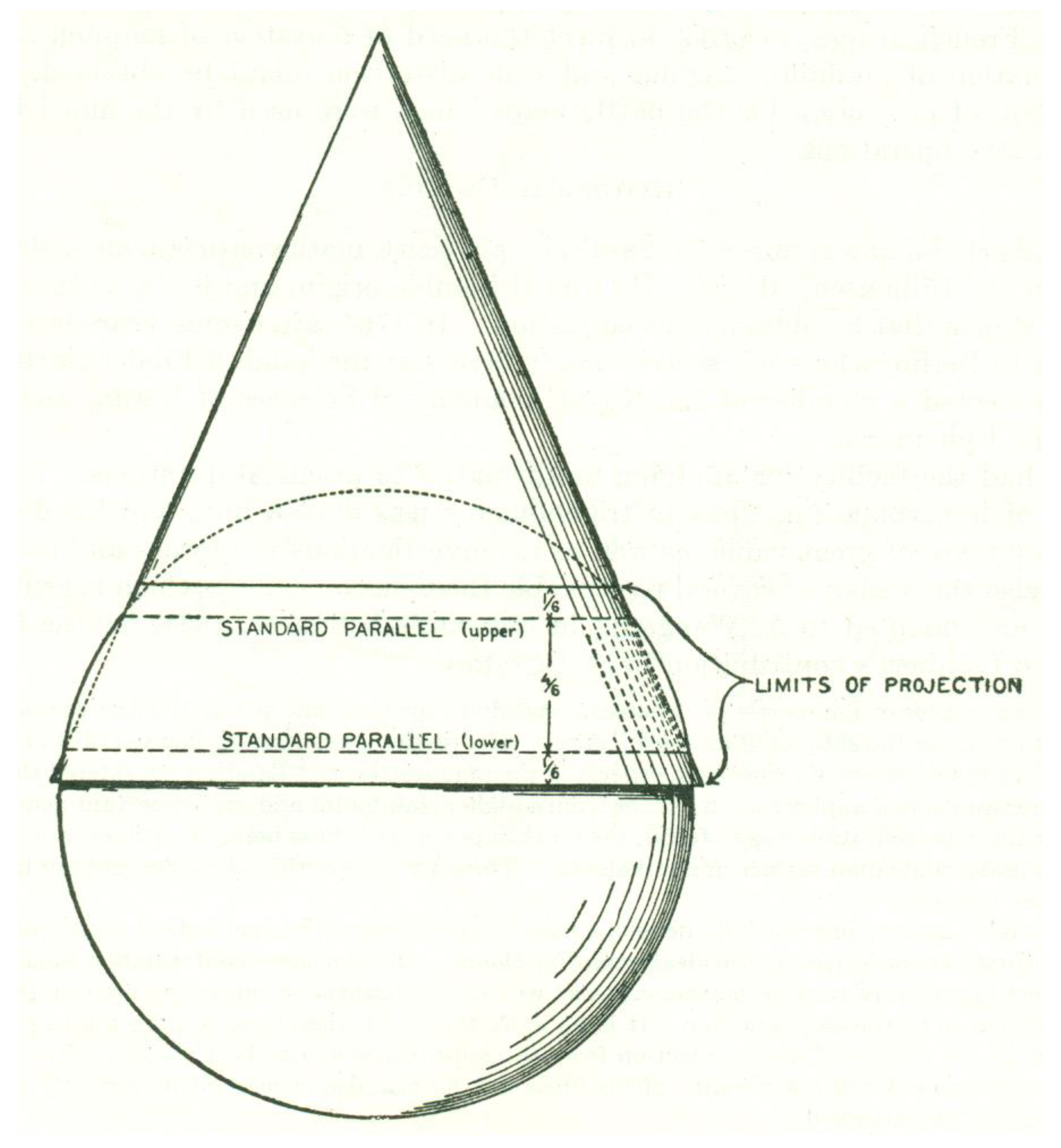
  • It is generally accepted that a secant projection is a mapping on an auxiliary surface that intersects a sphere or an ellipsoid and that the intersections of the secant conic and cylindrical projection are without deformations (Figure 3). Thus, for example, in ESRI’s dictionary [11][23], wresearchers were able to read: “Secant projection: A projection whose surface intersects the surface of a globe. A secant conic or cylindrical projection, for example, is recessed into a globe, intersecting it at two circles. At the lines of intersection, the projection is free from distortion.” This definition is not good. First, the intersection of two second-order surfaces is a fourth-order curve that generally does not consist of two circles. However, this shortcoming could be corrected by specifying the mutual position of the surface of the cone or cylinder and the sphere. However, the claim that the line of intersection of two surfaces is free of deformation cannot be an integral part of the definition because, in addition to being a claim, it is generally erroneous. However, it is so ingrained that it is almost regularly taken as true without evidence. The cited webpage is no longer available, but ESRI retains the term secant projection within the definitions of cylindrical and conical projections [11][23].
Geographies 02 00019 g003
Figure 3. Illustration of standard parallels as secant parallels. Source: Deetz and Adams [26][24], page 80. This is a misguided approach accompanied by the caption: "Diagram illustrating the intersection of a cone and sphere along two standard parallels". In other words, for Deetz and Adams (and many others) standard parallels and secant parallels are identical. The proof is missing, and this is a fake.

References

  1. Lambert, J.H. Part III, Section 6: Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten. In Beiträge zum Gebrauche der Mathematik und deren Anwendung; Verlag der Buchhandlung der Realschule: Berlin, Germany, 1772; Translated into English and introduced by W. R. Tobler as Notes and comments on the composition of terrestrial and celestial maps: Ann Arbor, Univ. Michigan, 1972, Mich. Geographical Publication no. 8, 125 p. Also reprinted in German, 1894, Ostwald’s Klassiker der Exakten Wissenschaften, no. 54: Leipzig, Wilhelm Engelmann, with editing by Albert Wangerin.
  2. d’Avezac, M.A.P. Coup d’oeil historique sur la projection des cartes de géographie: Société de Géographie. Bulletin 1863, 5, 257–361; discussion 438–485, Reprinted in Acta Cartographica, 1977, 25, 21–173.
  3. Snyder, J.P. Flattening the Earth: Two Thousand Years of Map Projections; The University of Chicago Press: Chicago, IL, USA; London, UK, 1993.
  4. Euler, L. De Repraesentatione Superficiei Sphaericae Super Plano; Academia Scientiarum Imperialis Petropolitanae: St. Petersburg, Russia, 1777; pp. 107–132, Latin. Translated into German as one of Drei Abhandlungen über Kartenprojection, in Ostwald’s Klassiker der Exakten Wissenschaften, no. 93: Leipzig, Wilhelm Engelmann, 1898, with editing by Albert Wangerin, pp. 3–37.
  5. De Lagrange, J.L. Sur la Construction des Cartes Géographiques: Nouveaux mémoires de l’Académie Royale des Sciences et Belles-Lettres de Berlin; 1779; pp. 161–210, Also in Oeuvres de Lagrange, 1869: Paris, Gauthier-Villars, v. 4, p. 635-692. Also in German, 1894, as Ueber die Construction geographischer Karten: Ostwald’s Klassiker der Exakten Wissenschaften, no. 55: Leipzig, Wilhelm Engelmann, p. 1-56, with editing by Albert Wangerin, pp. 82–97.
  6. Gauss, C.F. 1825, Allgemeine Auflösung der Aufgabe: Die Theile einer gegebnen Fläche auf einer andern gegebnen Fläche so abzubilden, daß die Abbildung dem Abgebildeten in den kleinsten Theilen ähnlich wird: Preisarbeit der Kopenhagener Akademie 1822. In Schumachers Astronomische Abhandlungen; Altona: Hamburg, Germany, 1825; pp. 5–30, Reprinted, 1894, Ostwald’s Klassiker der Exakten Wissenschaften, no. 55: Leipzig, Wilhelm Engelmann, pp. 57–81, with editing by Albert Wangerin, pp. 97–101.
  7. Tissot, N.A. Die Netzentwürfe Geographischer Karten, German ed.; Ernst Hammer: Stuttgart, Germany, 1887.
  8. Kraak, M.-J.; Roth, R.E.; Ricker, B.; Kagawa, A.; Le Sourd, G. Mapping for a Sustainable World; The United Nations: New York, NY, USA, 2020; Available online: https://unite.un.org/news/mapping-sustainable-world (accessed on 6 February 2021).
  9. Slocum, T.A.; McMaster, R.B.; Kessler, F.C.; Howard, H.H. Thematic Cartography and Geovisualization; Pearson Prentice Hall: London, UK, 2009.
  10. Šavrič, B.; Jenny, B.; Jenny, H. Projection Wizard—An Online Map Projection Selection Tool. Cartogr. J. 2016, 53, 177–185.
  11. Battersby, S. Map Projections. In The Geographic Information Science & Technology Body of Knowledge, 2nd Quarter 2017 ed.; Wilson, J.P., Ed.; USGIS: Ithaca, NY, USA, 2017. Available online: https://gistbok.ucgis.org/bok-topics/map-projections (accessed on 5 May 2022).
  12. Close, C.F.; Clarke, A.R. Map Projections. Encyclopaedia Britannica; Horace Everett Hooper: USA, 1911, 11th ed. Volume 17, pp. 653–663. Available online: https://www.gutenberg.org/files/42638/42638-h/42638-h.htm#ar1 (accessed on 25 May 2021).
  13. Lee, L.P. The Nomenclature and Classification of Map Projections. Emp. Surv. Rev. 1944, 7, 190–200.
  14. Škrlec, D. Geografski Informacijski Sustavi; Script, Faculty of Electrical Engineering and Computing; University of Zagreb: Zagreb, Croatia, 2000. (In Croatian)
  15. Clarke, K.C. Maps & Web Mapping; Kindle, Ed.; Pearson: London, UK, 2015.
  16. Lapaine, M. Behrmann Projection. In Proceedings of the 7th International Conference on Cartography and GIS, Sozopol, Bulgaria, 18–23 June 2018; pp. 226–235.
  17. Lapaine, М. Sekushchie paralleli v azimutal’nyh proektsiyah . Geod. Cartogr. Geod. I Kartogr. 2019, 80, 39–54. (In Russian)/Лапэн М.: Секущие параллели в азимутальных прoекциях // Геoдезия и картoграфия.–2019.–Т. 80.–No. 4.–С. 39–54.
  18. Lapaine, M.; Menezes, P. Standard, secant and equidistant parallels/Standardne, presječne i ekvidistantne paralele. Kartogr. I Geoinformacije/Cartogr. Geoinf. 2020, 19, 40–62.
  19. Van Sickle, J. GPS for Land Surveyors, 4th ed.; CRC Press: Boca Raton, FL, USA, 2015.
  20. Van Sickle, J. Map Projection, GEOG 862: GPS and GNSS for Geospatial Professionals, PennState College of Earth and Mineral Sciences, Department of Geography. 2017. Available online: https://www.e-education.psu.edu/geog862/node/1808 (accessed on 5 May 2022).
  21. Lapaine, M. Multi Standard-Parallels Azimuthal Projections. In Cartography—Maps Connecting the World; Robbi Sluter, C., Madureira Cruz, C.B., Leal de Menezes, P.M., Eds.; Springer International Publishing: Cham, Switzerland, 2015.
  22. Lapaine, M. Conic Projections with Three or More Standard Parallels. In Proceedings of the International Cartographic Association, 30th International Cartographic Conference, Florence, Italy, 14–18 December 2021; pp. 1–6.
  23. ESRI. GIS Dictionary. Available online: https://support.esri.com/en/other-resources/gis-dictionary (accessed on 14 March 2022).
  24. Deetz, C.H.; Adams, O.S. Elements of Map Projection with Application to Map and Chart Construction; U. S. Coast and Geodetic Survey Special Publication 68: Washington, DC, USA, 1934.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback