With the launch of Landsat 9 in September 2021, an optimal opportunity for in-flight cross-calibration occurred when Landsat 9 flew underneath Landsat 8 while being moved into its final orbit. Since the two instruments host nearly identical imaging systems, the underfly event offered ideal cross-calibration conditions. The purpoUse of this work was to use ing the underfly imagery collected by the instruments to estimate cross-calibration parameters for Landsat 9 for a calibration update scheduled at the end of the on-orbit initial verification (OIV) period was studied. Three types of uncertainty were considered: geometric, spectral, and angular (bidirectional reflectance distribution function—BRDF). Differences caused by geometric uncertainty were found to be negligible for this application.
- Operational Land Imager (OLI)
- Landsat
- ETM+
- PICS
- EPICS
- cross-calibration
- spectral band adjustment factor (SBAF)
- bidirectional reflectance distribution function (BRDF)
1. Introduction
1.1. Landsat 8 and 9 Characteristics
1.2. Cross-Calibration Based on Underfly Events
2. Sources of Uncertainty
The great advantage of an underfly maneuver is that the signal paths for the energy received by the sensors are nearly identical and, when the two sensors are also nearly identical, uncertainties in the measurements are minimized. However, they do still exist. From a signal-path perspective, the two sources of uncertainty are the pointing errors that may occur, and the differences in viewing/illumination geometry. Instrument errors are primarily due to spectral differences between the sensors. Each of these sources of uncertainty will be considered briefly in this section, and the quantified effects will help drive the data acquisition in the methodology section and the data analysis in the results section.2.1. Spectral Uncertainty
As the spectral filters for OLI and OLI-2 came from the original lot of filters developed for OLI, uncertainty from spectral differences was expected to be quite low. Figure 1 compares the spectral bandpasses, or relative spectral response (RSR) functions, for OLI and OLI-2 for several representative bands. It is clear that differences, though small, do exist.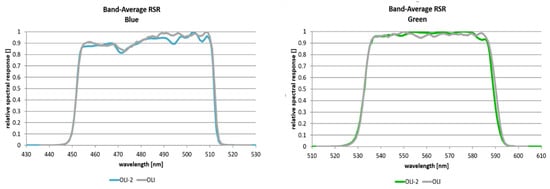
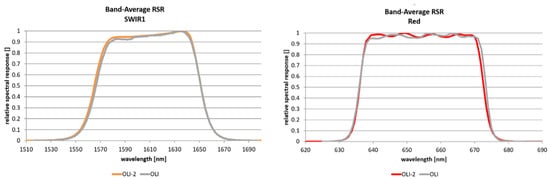

2.2. Geometric Uncertainty
Pointing differences between the two sensors systems were analyzed to determine the degree of uncertainty that would occur for this situation. An analysis was performed using Landsat 7/8 underfly data using pixel shifts between the scene pairs to determine how much any error in pointing would change the cross-calibration ratio. Results from this analysis are shown in Figure 3. In this figure, pixel shift between the images is on the horizontal axis while the resulting ratio of reflectances between the two images is plotted along the vertical axis. As pixel shift increases from zero to three, a small change in the calibration ratio occurs; it is largest in band 7, ranging from approximately 0.895 to 0.925 or a change of about 3.3%. To understand how much shift might occur between Landsat 8 and Landsat 9 images, experts on Landsat geometry were consulted at USGS EROS (Choate, Michael. Interview. Conducted by Dennis Helder, 23 June 2021). Results of that discussion indicated that image-to-image errors would be on the order of 5 m. Since Landsat GSD is 30 m, this represents a pixel shift of 0.16. As can be seen from Figure 3, this leads to a very small change in cross-calibration ratio. Thus, uncertainties due to pointing errors were deemed to be negligible for this application.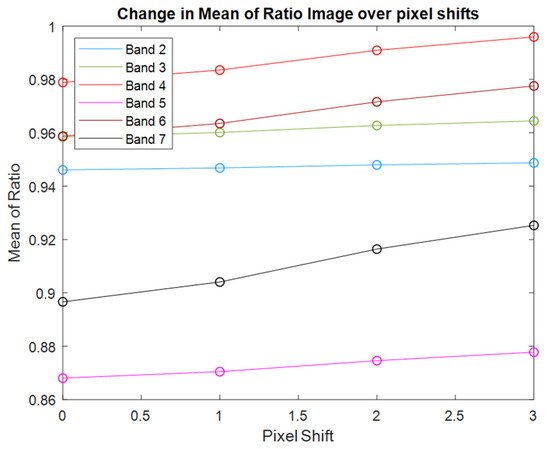
2.3. Angular Uncertainty
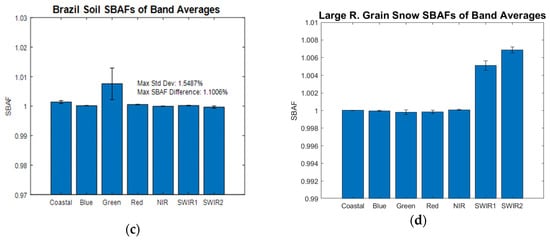
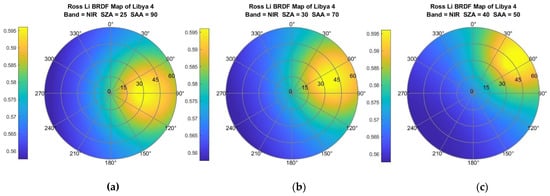
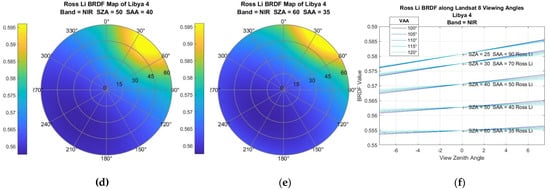
Even slight differences in viewing and illumination angles when observing a target will result in the sensors capturing slightly different reflectances. Reflectance of surfaces as function of viewing/illumination angle is modeled by target-specific bidirectional reflectance distribution functions (BRDF). Thus, to understand the uncertainty due to viewing angle differences, it was necessary to use a BRDF modeling approach. The Ross–Li BRDF model as used by the MODIS sensors was chosen, since it is broadly accepted by the remote-sensing community and a large amount of data exists [13,14,15][13][14][15]. However, drawbacks of this approach include the fact that the Ross–Li model was developed primarily for vegetation and the spatial resolution of the MODIS sensors is much larger than Landsat’s. To understand the impact of BRDF on the uncertainty for the underfly maneuver, a simple analysis was performed on two land cover types—a grassy pasture in east central South Dakota (well known to one of the authors) and desert sand (from the well-known Libya 4 calibration site). Examples of the BRDF models obtained from MODIS observations (the MCD43A1 MODIS product) of these locations in summer of 2021 are shown in Figure 4 and Figure 5. From these figures, wresearchers see that the hot spot (the yellow region indicating higher reflectance) follows the location of the sun azimuthally and moves away from the origin as the SZA increases. Note that Landsat viewing angles are restricted to a region well within the 15° annular ring (±7.5°) and lie along a line roughly from 98° to 278°. If one extracts the data along this line and plots them as a function of VZA, the plot in the lower-right corner of the figure results. The key results to note here are that when VZA is restricted to the narrow range of Landsat angles, the curves are very linear. Secondly, as the VAA moves further from the principal plane, the slope of the lines decreases. Conversely, even for small VZA differences, the change in BRDF becomes large very quickly. Analysis of these VZA differences indicated that when the VZA difference reaches 7°, the change in BRDF value can reach 6% or more depending on SZA and relative azimuth angle. Clearly, BRDF uncertainty is unacceptably large for cross-calibration purposes! Similar results were obtained for the Libya 4 site, which is much more Lambertian in nature than a vegetative site. Figure 5 shows the same type of linear relationship (graph in lower right), and also less sensitivity—in this case, BRDF uncertainty only reached 1.5% at a VZA difference of 7°.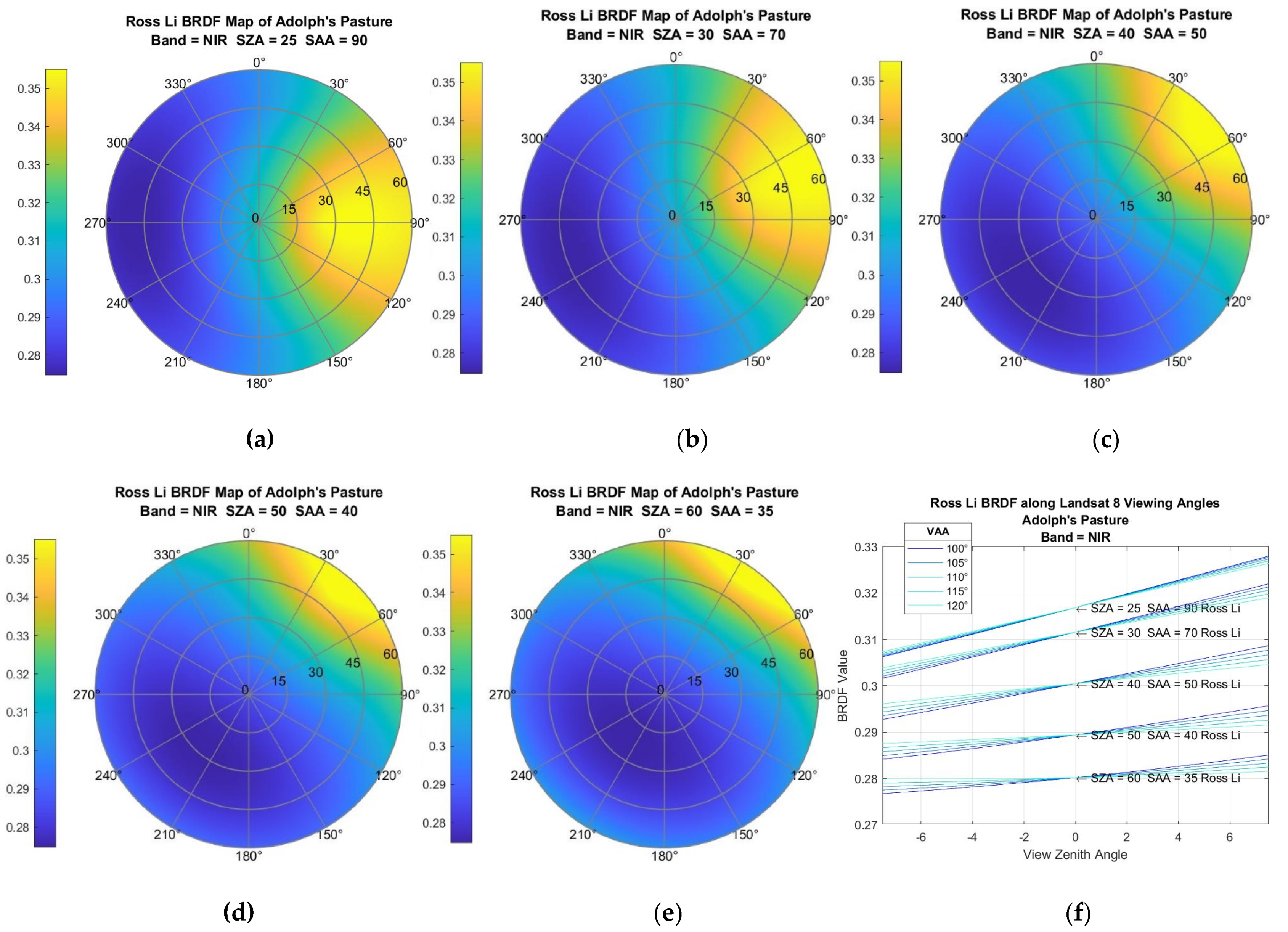

References
- Masek, J.G.; Wulder, M.A.; Markham, B.; McCorkel, J.; Crawford, C.J.; Storey, J.; Jenstrom, D.T. Landsat 9: Empowering open science and applications through continuity. Remote Sens. Environ. 2020, 248, 111968.
- MarkhamM, B.; McCorkel, J.; Montanaro, M.; Morland, E.; Pearlman, A.; Pedelty, J.; Wenny, B.; Barsi, J.; Donley, E.; Efremova, B.; et al. Landsat 9: Mission Status and Prelaunch Instrument Performance Characterization and Calibration. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5788–5791.
- Metzler, M.D.; Malila, W.A. Characterization and comparison of Landsat-4 and Landsat-5 Thematic Mapper data. Photogramm. Eng. Remote Sens. 1985, 51, 1315–1330.
- Teillet, P.M.; Markham, B.L.; Barker, J.L.; Storey, J.C.; Irish, R.R.; Seiferth, J.C. Landsat sensor cross-calibration using nearly coincidental matching scenes. In Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VI; SPIE: Bellingham, WA, USA, 2000; Volume 4049.
- Mishra, N.; Haque, M.O.; Leigh, L.; Aaron, D.; Helder, D.; Markham, B. Radiometric Cross Calibration of Landsat 8 Operational Land Imager (OLI) and Landsat 7 Enhanced Thematic Mapper Plus (ETM+). Remote Sens. 2014, 6, 12619–12638.
- Teillet, P.M.; Fedosejevs, G.; Thome, K.J.; Barker, J.L. Impacts of spectral band difference effects on radiometric cross-calibration between satellite sensors in the solar-reflective spectral domain. Remote Sens. Environ. 2007, 110, 393–409.
- Chander, G.; Mishra, N.; Helder, D.L.; Aaron, D.; Choi, T.; Angal, A.; Xiong, X. Use of EO-1 Hyperion data to calculate spectral band adjustment factors (SBAF) between the L7 ETM+ and Terra MODIS sensors. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010.
- Thenkabail, P.; Aneece, I. Global Hyperspectral Imaging Spectral-Library of Agricultural Crops for Conterminous United States V001 . NASA EOSDIS Land Processes DAAC, 2019. Available online: https://lpdaac.usgs.gov/products/ghisaconusv001 (accessed on 20 March 2021).
- Meerdink, S.K.; Hook, S.J.; Roberts, D.A.; Abbott, E.A. The ECOSTRESS spectral library version 1.0. Remote Sens. Environ. 2019, 230, 111196.
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER Spectral Library Version 2.0. Remote Sens. Environ. 2009, 113, 711–715.
- World Agroforestry (ICRAF); International Soil Reference and Information Centre (ISRIC). ICRAF-ISRIC Soil VNIR Spectral Library. In World Agroforestry—Research Data Repository, V1; World Agroforestry (ICRAF): Nairobi, Kenya, 2021.
- Salvatori, R.; Salzano, R.; Franco, S.D.; Fontinovo, G.; Plini, P. SISpec 2.0 Snow-Ice Spectral Library; National Research Council of Italy, Institute of Polar Sciences: Rome, Italy, 2020.
- Wanner, W.; Li, X.; Strahler, A.H. On the derivation of kernels for kernel-driven models of bidirectional reflectance. J. Geophys. Res. Atmos. 1995, 100, 21077–21089.
- Wanner, W.; Strahler, A.H.; Hu, B.; Lewis, P.; Muller, J.-P.; Li, X.; Schaaf, C.L.B.; Barnsley, M.J. Global retrieval of bidirectional reflectance and albedo over land from EOS MODIS and MISR data: Theory and algorithm. J. Geophys. Res. Atmos. 1997, 102, 17143–17161.
- Lucht, W.; Schaaf, C.B.; Strahler, A.H. An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote Sens. 2000, 38, 977–998.
