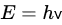Quantum mechanics is a mathematical formalism that models the dynamics of physical objects. It deals with the elementary constituents of matter (atoms, subatomic and elementary particles) and of radiation. It is very accurate in predicting observable physical phenomena, but has many puzzling properties. The foundations of quantum mechanics are a domain in which physics and philosophy concur in attempting to find a fundamental physical theory that explains the puzzling features of quantum mechanics, while remaining consistent with its mathematical formalism. Several theories have been proposed for different interpretations of quantum mechanics. However, there is no consensus regarding any of these theories.
Quantum mechanics began in 1900, when Max Planck found a formula that fit the experimental data of the radiation emitted by a black body. Contrary to classical physics, Planck’s formula suggests that radiation is emitted in definite packets of energy called ‘quanta’. Whether discontinuity of radiation is clearly implied by black-body radiation is still debated; see Passon and Grebe-Ellis [1] and the references therein for this debate. What is relevant here is that the energy, E, of each packet is proportional to the frequency, ν, of the radiation, and the constant of proportionality is a fundamental constant, called Planck’s constant, h [2]. Planck’s formula is defined as follows:
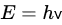
Quantum mechanics clarifies many startling features usually encountered in the microcosmic realm. These astonishing features were best illustrated by the double-slit experiment. It involves the firing of particles, such as electrons, one by one on a plate in which there are two slits, A and B. The particles arrive one by one, such that single random impacts are registered on a detecting screen beyond the plate. However, the collective outcome of a large number of impacts on the detecting screen reveals an interference pattern of alternating dark and light bands. Such a collective pattern is characteristic of particles behaving as incoming waves from both slits. Meanwhile, the interference pattern has been built up out of a succession of separate and independent individual impacts.
Once detectors are placed at slits A and B to determine the slit through which each particle goes, the interference pattern ceases to exist. This strange feature seems to unintuitively suggest that each particle passes through both slits when there are no detectors and through only one slit when detectors are present
[3][4][3,4].
Thus, it seems impossible to observe interference and simultaneously determine which slit the particle has passed through.
The formal explanation of such phenomena, as well as many others, started in 1925 with the advent of matrix mechanics developed by Werner Heisenberg, and several months later, with that of wave mechanics developed by Erwin Schrödinger. Matrix mechanics and wave mechanics are mathematically equivalent, although the mathematical formalism of the latter was more familiar to physicists at that time. Matrix mechanics interprets the states of a physical system by matrices that evolve in time, whereas wave mechanics interprets these states by wavefunctions governed by a linear differential equation.