Mechanics and Mathematics in Ancient Greece

Mechanics and Mathematics in Ancient Greece: Comparison

Please note this is a comparison between Version 4 by Vicky Zhou and Version 3 by Vicky Zhou.

This entry presents an overview on how mechanics in Greece was linked to geometry. In ancient Greece, mechanics was about lifting heavy bodies, and mathematics almost coincided with geometry. Mathematics interconnected with mechanics at least from the 5th century BCE and became dominant in the Hellenistic period. The contributions by thinkers such as Aristotle, Euclid, and Archytas on fundamental problems such as that of the lever are sketched. This entry can be the starting point for a deeper investigation on the connections of the two disciplines through the ages until our present day.

mechanics
mathematics
natural philosophy
Aristotle
Euclid

1. Introduction

The link of mathematics with mechanics is ancient and complex enough to be given a thorough and neat explanation. The same terms ‘mechanics’ and ‘mathematics’ today have a very different meaning with respect to that in ancient times. In particular, herein, we focus on their meaning and relations in classical and Hellenistic Greece.

Actually, the ancient Greek term μεχανη meqanh (‘mechane’) indicated the discipline that dealt with equipments, in particular those for lifting weights. However, the meaning is not limited to this and in general also encompasses other inventions. As for mathematics, the question is more complex: as a matter of fact, it is not even clear how Pythagoras and Thales, for example, intended their discipline; moreover, there are no mathematical treatises before Plato (4th century BCE), even though during the last half of the 5th century BCE, there were meaningful testimonials of a handful of mathematicians intensely concerned with geometrical problems. This period is named the Heroic Age of Mathematics in ^[1] (p. 42.): its main characters were Archytas of Tarentum (b. c. 428 BCE), Hippasus of Metapontum (f. c. 480 BCE), Democritus of Abdera (b. c. 460 BCE), and Hippocrates of Chios (b. c. 470 BCE). In any case, the mathematicians of the 4th century that attended Plato’s Academy also left no written epistemological considerations: Taethetus of Athen (c. 314-c. 369 BCE), Theodorus of Cyrene (b. c. 390 BCE), Eudoxus of Cnidus (d. c. 355 BCE), Menaechmus (f. c. 350 BCE), and Autolycus of Pitane (f. c. 330 BCE), see for instance ^[1][2].

On the other hand, Aristotle’s position is clear, probably interpreting the thought of the important mathematicians of his time:

[.] as the mathematician investigates abstractions (for before beginning his investigation he strips off all the sensible qualities, e.g., weight and lightness, hardness and its contrary, and also heat and cold and the other sensible contrarieties, and leaves only the quantitative and continuous, sometimes in one, sometimes in two, sometimes in three dimensions, and the attributes of these qua [i.e., inasmuch] quantitative and continuous, and does not consider them in any other respect, and examines the relative positions of some and the attributes of these, and the commensurabilities and incommensurabilities of others, and the ratios of others; but yet we say there is one and the same science of all these things—geometry), the same is true with regard to being.

^[3] (11, 3. 27)

Here, mathematics seems to be identified with geometry, but in other passages of Aristotle’s writings, the meaning of the term is broader and also applies to optics, astronomy, and music, which Aristotle considered subordinate to geometry (optics and astronomy) and arithmetic (music):

Similar evidence is supplied by the more physical of the branches of mathematics, such as optics, harmonics, and astronomy. These are to some extent the converse of geometry. While geometry investigates physical lines but not qua physical, optics investigates mathematical lines, but qua physical, not qua mathematical.

^[4] (II, 194a, 7 ff.)

In another point of Aristotle’s writings mechanics as well appears as a subordinate science, thus another form of mathematics:

The same account may be given of harmonics and optics; for neither considers its objects qua sight or qua voice, but qua lines and numbers; but the latter are attributes proper to the former. And mechanics too proceeds in the same way.

^[3] (M, 3, 1078a)

It is not known why Aristotle exposed this thesis, as the mathematical treatment of mechanics was for sure more recent to him than that of the other subordinate sciences. It is probable that Archytas of Tarentum was the first to introduce a geometric study of mechanics, perhaps limited to the lever. This is what Diogenes Laertius (c. 200 CE) wrote on the subject much time later:

He was the first to bring mechanics to a system by applying mathematical principles; he also first employed mechanical motion in a geometrical construction, namely, when he tried, by means of a section of a half-cylinder, to find two mean proportionals in order to duplicate the cube. In geometry, too, he was the first to discover the cube, as Plato says in the Republic.

^[5] (volume 2, book 8, 83, pp. 395–396)

It is unlikely that Aristotle was referring to his own studies as the Mechanica problemata (see below): indeed, it is true that this treatise employs geometry, but it is also of dubious attribution and of uncertain dating.

2. Aristotle’s Mechanica Problemata

The first mathematical treatise on mechanics known today is precisely the Mechanica Problemata ^[6]. It has been proved that the Arab world knew the treatise or at least a part of it ^[7]. During the Middle Ages and the Renaissance, the attribution to Aristotle was substantially undisputed; an investigation on the Renaissance is in ^[8], while for more recent periods see ^[9]. It is worth noticing that Fritz Kraft considers the Mechanica Problemata to be an early work by Aristotle, when he had not yet fully developed his physical concepts ^[10], while a recent paper by Thomas Nelson Winter considers Archytas of Tarentum as the author of the Mechanica Problemata ^[11]; some more investigations are in ^[12]. This last attribution is suggestive, though not very convincing. A possibility, not exploited indeed in the literature, is that the Mechanica Problemata is based on a previous text written by Archytas of Tarentum and subsequently elaborated in an Aristotelian environment. Here, we do not enter into the merit of this attribution, and for the sake of simplicity, we consider the Mechanica Problemata as an Aristotelian work instead of a pseudo-Aristotelian one, as it is frequently seen. For the same reasons of simplicity, we do not comment the great relevance assumed by the Aristotelian treatise in the Renaissance and the role it had in the history of mechanics; for this, reference can be made to ^[9][13].

The treatise can be divided into two parts: one theoretical and one applicative. In the theoretical initial part, the law of the lever is proved, and geometry openly insinuates into Aristotle’s physics, leading to a proof based on intuition and analogy more than on a rigorous argumentation, as was customary among the mathematicians of the time. Starting from the law of the lever, the second part presents the qualitative and quantitative behavior of simple machines: the screw, the pulley, the wedge, and the winch (according to how they have been called subsequently in history).

In the following section, we go into some detail in the demonstration of the law of the lever, trying to understand its weaknesses and strengths without being influenced by modern notions. However, before commenting the treatise, we consider noteworthy to reproduce its incipit in the form we know:

One marvels at things that happen according to nature, to the extent the cause is unknown, and at things happening contrary to nature, done through art for the advantage of humanity. Nature, so far as our benefit is concerned, often works just the opposite to it. For nature always has the same bent, simple, while use gets complex. So whenever it is necessary to do something counter to nature, it presents perplexity on account of the difficulty, and art [τεχνη, techne] is required. We call that part of art solving such perplexity a mechane.

^[11] (p. 1)

This incipit is quite ‘exotic’ for a modern mathematician, and we suppose also for mathematicians contemporary to Aristotle, who is much more sober in his philosophical writings. Indeed, Aristotle’s basic idea on moving bodies is:

Now if of two objects moving under the influence of the same force one suffers more interference, and the other less; it is reasonable to suppose that the one suffering the greater interference should move more slowly than that suffering less.

^[6] (p. 341)

In this argument, the two terms force and interference have a vague meaning, which is fine only for a natural philosopher wishing to provide qualitative explanations but not for a mathematician. The locution more slowly refers to a motion along the arc of circle and means that in a given finite time the arc of circle passed is shorter. To make this argument more precise and susceptible of a quantitative treatment, Aristotle, or whoever for him, introduced geometry to explain the meaning of the term ‘interference’. Note that this is the first written testimonial in which mathematics was used in mechanics.

The proof is based on Figure 1, where we report two representations of Aristotle’s argument, since we do not have original drawings but only graphical interpretations provided by translators and commentators, see for instance ^[14]. Figure 1a is the more interesting one for us, as commented hereinafter; Figure 1b is the one more commonly found in the Renaissance editions of the Mechanica Problemata. Aristotle assumes a clockwise motion on the circumference starting from B and labels the motions Z

Θ

and KH, parallel to the tangent to the circumference, as ‘according to nature’; he labels the motions XZ, BY along the radius of the same circumference, as ‘against nature’. This denomination makes it natural in referring to Figure 1a, where the ‘natural’ motion is vertical and directed downward, just like that of a falling weight, to which Aristotle referred constantly in his philosophy of nature.

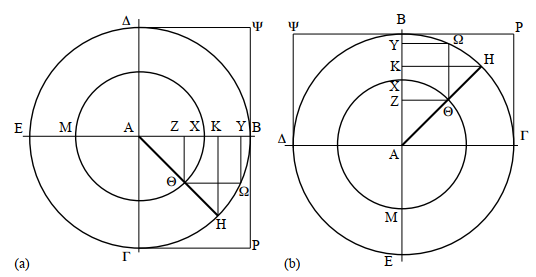
Figure 1. Vertical (a) and horizontal (b) motion according to nature

Geometry proves that, in correspondence with the same natural motion Z, themotion against nature decreases as the radius of the circle increases, since YB < ZX. Basically, what Aristotle said is that a body under a given force and constrained to move along a circumference moves faster the greater the radius of the circumference, because the deviation (the interference to motion) is smaller.

The other term that needs to be justified is force (ισχν'ος). The term used by Aristotle seems to refer to muscular force but on some occasions, more or less explicitly, identifies weight, which, like muscular force, exerts a dragging action. One can then paraphrase Aristotle saying that “a body of given weight constrained to move along a circumference moves faster the greater the radius of the circumference”.

So far the reasoning is quite rigorous, but rigor fails when Aristotle tried to apply this result for a quantitative law of the lever, proposed in Problem 3 (the numbering of problems is different from edition to edition; here, we chose in ^[6]), where he states:

[.] the ratio of the weight moved to the weight moving it is the inverse ratio of the distances from the centre.

^[6] (p. 353)

This is the quantitative formulation of the law of equilibrium for the lever; however, Aristotle added nothing to common man knowledge, since that law was for sure known since a long time, based on simple observations and the knowledge of a little mathematics. More interesting is the explanation:

The reason has been given before that the point further from the centre describes the greater circle, so that by the use of the same force, when the motive force is farther from the lever [sic! correct: fulcrum], it will cause a greater movement.

^[6] (p. 353)

To a modern reader this does not seem like a rigourous explanation but simply a kinematical description of the phenomenon, which becomes causal and dynamical if one admits that there is a dragging effect of the weight that increases with its distance from the fulcrum. This can be suggested by the use of the term ‘motive force’ for one of the two weights of the lever; more explicitly, Winter translated the last part of the previous quotation as: “So by the same force, the mover will manage more the farther from the fulcrum” ^[11] (p. 11).

However, also accepting this view, one can correctly formulate only this rule: “a weight p located at a distance d > D from the fulcrum can raise a weight P > p located at a distance D”, which is an indeterminate law, as remarked by Bernardino Baldi (1553-1617 CE):

Thus when Aristotle discloses the reason for which the lever moves a weight more easily, he says that this happens because of the greater length on the side of the power that moves; and this [accords] quite well with his first principle, in which he assumes that things at the greater distance from the centre are moved more easily and with greater force, from which he finds the principal cause in the velocity with which the greater circle overpowers the lesser. So the cause is correct, but it is indeterminate; for I still do not know, given a weight and a lever and a force, how I must divide the lever at the fulcrum so that the given force may balance the given weight. Therefore Archimedes, assuming the principle of Aristotle, went on beyond him; nor was he content that the force be on the longer side of the lever, but he determined how much [longer] it must be, that is, with what proportion it must answer the shorter side so that the given force should balance the given weight.

^[15] (pp. 54–55. Translation by ^[16], p. 14)

For the indeterminate law to become determinate, one needs to replace the relations of greater or lesser with an equality and to allow the variation of the value of the moving weight, so as to give: “a heavy body P brings about an action on another body Q, located on the opposite side of a lever, which is directly proportional to its distance d from thefulcrum and to its weight p”; in modern terms, it is the product dp that actually counts.

It is worth remarking that in the explanation of the law of the lever the circumstance that “the mover will manage more the farther from the fulcrum” is stressed more than the balance between the tendency to go down of the two weights on the lever. This is the same occurring in the Middle Age treatise Ration

attributed to Jordanus Nemorarius (13th century CE) ^[13] (p. 84).

Assuming the lever of Figure 2, one can accept that there is an equilibrium when two weights G are located at the same distance from the fulcrum A (that is, AB = AM) for symmetry reasons. However, the weight G at M can be replaced by a weight D at a distance AE such that AE × D = AM × G = AB × G, which is the law of the lever in its standard formulation.

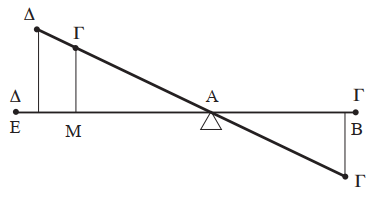
Figure 2. The law of the lever.

3. Euclid’s Book on the Balance

We present the proof of the law of the lever contained in The Book of the Balance which can be attributed, with much reserve, to Euiclid Age

of AlMathexandria matics

^[171]

(p. 42.): its main characters were Archytas of Tarentum (b. c. 428 BCE), Hippasus of Metapontum (f. c. 480 BCE), Democritus of Abdera (b. c. 460 BCE), and Hippocrates of Chios (b. c. 470 BCE). In any case, the mathematicians of the 4th century that attended Plato’s Academy also left no written epistemological considerations: Taethetus of Athen (c. 314-c. 369 BCE), Theodorus of Cyrene (b. c. 390 BCE), Eudoxus of Cnidus (d. c. 355 BCE), Menaechmus (f. c. 350 BCE), and Autolycus of Pitane (f. c. 330 BCE), see for instance

^[181]. Doubts arise as no work by Euclid on mechanics exists in Greek, nor is he credited with any mechanical work by ancient writers. In 1851, Woepcke published an Arabic fragment that he had discovered in Paris under the title Le livre d’Euclide sur la balance ^[192], attributing it to Euclid. If that were a treatise of Euclid, it would be the first on mechanics after the Mechanica Problemata, less than one century later, and would be worthy to be commented on here, as we do.

Euclid’s treatise has received little attention from the historians, most probably because of the dubious attribution; when speaking about the Greek proof of the law of the lever, reference is made only to the Equilibrium of Planes by Archimedes ^[20]. A recent discussion on The Book of the Balance can be found in ^[21], but the most interesting account is still due to a Pierre Duhem at the beginning of the 20th century ^[22] (volume 1, pp. 62–67). Duhem criticized Euclid’s proof bitterly for his confusing argumentations; however, we do not agree with this position and consider the proof as interesting and smart as that proposed by Archimedes at least. In addition, it has the advantage of not requiring notions that cannot be found in the treatise, as it is instead the case for the notion of center of gravity, necessary in the Equilibrium of Planes.

On the other hand, Aristotle’s position is clear, probably interpreting the thought of the important mathematicians of his time:

The treatise is very terse, completely different from the wordy Mechanica Problemata. As usual in Greek writings on geometry, there are definitions (1), axioms (2), and propositions (4), not present in the Aristotelian treatise. Apart from the logical structure, the main difference with the Mechanica Problemata is that here there are no references to principles of a pre-established philosophy of nature, as it occurs also for a modern treatise on physical mathematics, after two thousand years. Moreover, the axioms in The Book of the Balance, although not necessarily shared by everyone at a first reading, are verifiable with simple experiments, even mental ones.

The definition and the axioms are referred to below:

Definition 1. Weight is the measure of the heaviness and lightness of one thing compared to another by means of a balance.

Axiom 1. When there is a straight beam of uniform thickness, and there are suspended on its extremities two equal weights, and the beam is suspended on an axis at the middle point between the two weights, then the beam will beparallel to the plane of the horizon.

Axiom

[.] as the mathematician investigates abstractions (for before beginning his investigation he strips off all the sensible qualities, e.g., weight and lightness, hardness and its contrary, and also heat and cold and the other sensible contrarieties, and leaves only the quantitative and continuous, sometimes in one, sometimes in two, sometimes in three dimensions, and the attributes of these qua 2

. When two weights—either equal or unequal—are placed on theextremities of a beam, and the beam is suspended by an axis on some position of it such that the two weights keep the beam on the plane of the horizon, then if one of the two weights is left in its position on the extremity of the beam and from the other extremity of the beam a straight line is drawn at a right angle to the beam in any direction at all, and the other weight is suspended on any point at all of this line, then the beam will be parallel to the plane of the horizon as before [. . . ]

[i.e., inasmuch] quantitative and continuous, and does not consider them in any other respect, and examines the relative positions of some and the attributes of these, and the commensurabilities and incommensurabilities of others, and the ratios of others; but yet we say there is one and the same science of all these things—geometry), the same is true with regard to being.

^[193] (p. 220. Translation into English in ^[18])

(11, 3. 27)

At least two other axioms, very intuitive indeed, are implicit:

Axiom

Similar evidence is supplied by the more physical of the branches of mathematics, such as optics, harmonics, and astronomy. These are to some extent the converse of geometry. While geometry investigates physical lines but not qua 3’

. Suspending any weight at the fulcrum, if the balance is horizontal it will remain horizontal.

Axiom

physical, optics investigates mathematical lines, but qua 4’.

Weight is an additive measure. That is, given two heavy bodies with equal weight, the heavy body composed by the two bodies has a double weight.

The lack of Axiom 3’ is also noticed in ^[22] (volume 1, p. 65).

Before moving on to the analysis of the propositions, a short comment is necessary. For instance, it should be noted that the axioms refer explicitly to weights and they do not contain the term force, which, on the other hand, was used frequently in the Mechanica problemata, thus reducing the ambiguity of the Aristotelian treatise. Then, at first sight for a modern reader, Axiom 1 seems to be a simple reformulation of the Definition, because it can be immediately derived from it; however, this is not the case. Actually, in the Definition, the equality of the measure of the two weights is verified operationally and can be carried out with whatever a balance, even with one having different lever arms: two heavy bodies are considered to be of equal weight (that is, of the same degree of heaviness) if and only if when placed on the same plate of a scale they are balanced by the same heavy body placed on the other plate.

Moreover, Axiom 1 is not self-evident as it might seem at first sight; in fact, although the arms of the balance are equal, the two heavy bodies at the extremities can be of different shape and material, even if with the same weight: therefore, the principle of symmetry cannot be invoked. It could be said that Axiom 1 has the function of establishing that as far as equilibrium is concerned, the only relevant characteristic of a body is its weight.

Axiom 2 is somewhat complex and unpredictable: it states that if the axis of a balance is in a horizontal position under the action of some weights, it remains in that position even if the weights it supports are moved in any direction perpendicular to it. Figure 3 illustrates two possibilities of displacing the weights: in Figure 3a, the displacement is vertical, and the statement of Axiom 2 can be easily accepted. The case of Figure 3b is different; here, the fact that the axis-weight system is not in equilibrium, since there is a moment that tends to make the axis of the scale rotate around itself, is disturbing somehow. However, Axiom 2 does not say that the balance is in equilibrium but only that it remains horizontal.

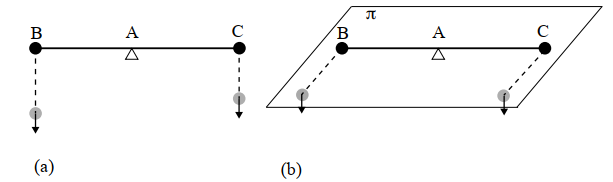
Figure 3. Displacement of weights orthogonal to the beam in a vertical (a) and a horizontal (b) plane.

As for the propositions, we focus mainly on the first:

physical, not qua mathematical.

Proposition 1. This being assumed, we pose a straight line AB (see Figure 4) as a beam of a balance whose axis is at point C, and we draw CE at a right angle to line AB, and we extend it in a straight line to point D, and we make line CD equal to CE, and we complete the square CH by drawing parallels. Then we place equal weights at points A, H and E. And so I say that these three weights keep lines AB, ED parallel to the horizon.

The proof is this: tne weight has been placed on one of the extremities of line AB at point A. From the other extremity we have drawn a line at right angles, the line BH, and we have placed on it a weight equal to the weight which is at point A. And so the two weights maintain the line AB parallel to the horizon [by Axiom II]. For the same reason it is necessary that the two weights which are at points E, H keep line ED parallel to the horizon. Thus weights A, E, H will keep lines AB, ED parallel to the horizon.

It is clear that if the weight which is at point H is removed to point B from which the line BH was drawn at right angles, then with weight A it maintains line AB parallel to the horizon, just as it was necessary when the weight was at point H. The line ED will accordingly not be in equilibrium, since the weight E will make it incline on its side. But if weight E is moved to point C, or if weight E is left on its place and a weight equal to it is placed at point D, then the weight E balances the line ED and it will be parallel to the horizon. We conclude from this that the weight which is at point H was one weight which stood in place of two weights at points B, D, each of which was equal to it.

^[194] (p. 221. Translation into English in ^[18])
(II, 194a, 7 ff.)

Figure 4 illustrates the configuration of the lines ACB, CDE, BH, and DH drawn on a horizontal plane, so that the direction of gravity is perpendicular to the same plane. The proof of Proposition 1 is simple, even if it is not clear what its role is in the proof of the law of the lever. This approach is different from that in Aristotle’s text and is typical of Greek geometry, in which without an initial comment explaining the strategy, a series of propositions are shown, the purpose of which is revealed only at the end.

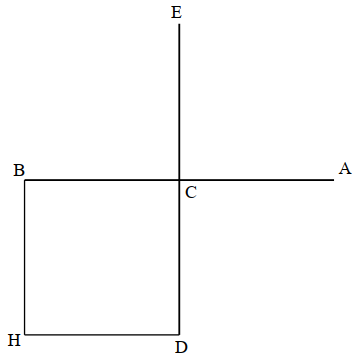
In another point of Aristotle’s writings mechanics as well appears as a subordinate science, thus another form of mathematics:

Figure 4. Equilibrium of a beam in the space. Redrawn from [19], p. 221.

Proposition 2 follows immediately from Proposition 1 and states that the equal arm balance of Figure 5a, with the fulcrum in C, is in equilibrium under three equal weights, one placed at the free end H, one at a distance CZ from the fulcrum, and the last at a distance TW from the free end H, so that CZ = WT. Then, since CZ and WT are arbitrary, the proposition allows us to affirm more generally that in a balance in equilibrium under three equal weights such as that in Figure 5a, the two weights hanging from the same arm can be shifted in opposite directions by the same amount (notice that if there is equilibrium for CZ = WT, there cannot be equilibrium for CZ 6= WT).

Figure 5. Equilibrium of a beam under three weights: (a) a modern interpretation; (b) appealing to the law of the lever; (b) is redrawn from ^[19], p. 222.

The proof refers to Figure 5b, in which the lines are supposed as drawn on a horizontal plane. Three equal weights are hung at points A, E, and H, where A can be thought as belonging to the equal arm balance ACB. The circles serve only to facilitate the reading of the drawing. According to Proposition 1, the three weights are in equilibrium: indeed, even if Proposition 1 was proved when the quadrilateral BCDH of Figure 4 is a square, it is easy to prove it holds also valid for a rectangle such as ATEC in Figure 5b. If the three equal weights are in equilibrium with respect to the balance ACB, the plane to which they belong is also in equilibrium. Thus, the straight line HT can be considered the axis of a balance with fulcrum in C to which the weights in A, E, and H are somehow hung, and is also in equilibrium. By Axiom 2, the two weights in A and E can be translated orthogonally to HCT, respectively, to Z and W, and HT remains horizontal: thus, the balance HCT with weights in H, Z, and W is in equilibrium.

Proposition 2 is not completely sufficient to prove the law of the lever; however, it suggests the following generalization, which can be assumed as a further axiom:

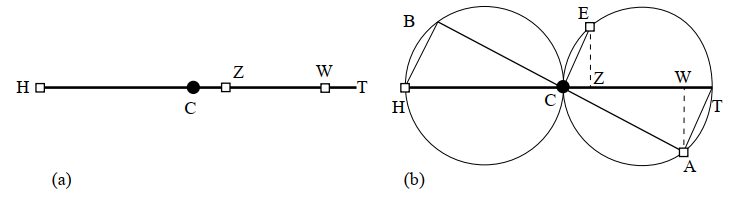
Axiom 5’. If any number of weights keep a balance in the horizontal position and two weights hanging at one of the two arms are moved in the opposite direction of the same amount, the balance still remains in the horizontal position.

This should be considered as an axiom because Proposition 2 proves a similar statement for the case of three weights only, two of them on one arm of the balance. Duhem considered Propositions 1 and 2 useless, referring to them as “parasitic and vicious” ^[22] (p. 65), and assumed only Axiom 5’. Actually, Propositions 1 and 2 are very interesting, because they show how a mathematician can tackle a mechanical proof: without them, Axiom

The same account may be given of harmonics and optics; for neither considers its objects qua sight or qua voice, but qua 5’

could be hardly imagined. Moreover, Proposition 2 let the law of the lever be proved at least for a ratio 1 : 2 of weights at the ends. Indeed, if the straight lines ACB and TCH are at p/4, the weights in Z and W coalesce in the middle of the arm CD, providing a weight double than that in A.

At this point, the law of the lever can be easily proved in Proposition 4, with reference to Figure 6a. The balance HCE is in equilibrium by Axiom 1 if two equal weights p are hung at H and E and two weights are suspended below the fulcrum C.

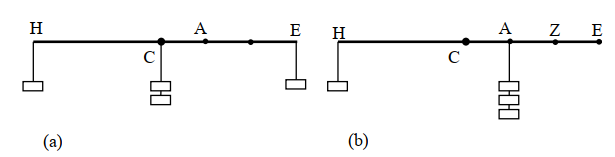
Figure 6. The law of the lever for a particular case: (a) first step of the proof; (b) second step of the proof; (b) is redrawn from ^[18], p. 27.

Due to Proposition 2, we can move the weight p in C to position A and the weight p in E to position Z without altering equilibrium (we could already start from the position with the weights in A and Z, in equilibrium according to Proposition 2). Then, one can repeat the operation moving another weight p from C to A and the weight p from Z to A; this can be performed in accordance with Axiom 5’ but not with Proposition 2, because on the arm CE, there are more than two weights. Thus, we obtain the configuration of Figure 6b with three equal weights in A, which for Axiom 4’ are equivalent to a weight having a triple value of the weight in B. The law is thus proved for a weight ratio of 3 : 1, and Euclid leaves to the reader the generalization of the law of the lever to the more general case of the ratio of weights expressed by any pair of integers.

A separate discussion is needed for Proposition 3, which is enunciated and proven by means of Figure 7, illustrating a balance BCA of equal arms with fulcrum in C, in equilibrium under three equal weights applied in B, Z, and D. The 10 segments into which BA is divided are all equal.

Figure 7. The force of weight. Redrawn from [19], p. 223.

Proposition 3 states that one can shift the weight at B onto T and the weight at D onto E, still keeping the balance horizontal. It is in fact a shorter balance than the previous one, for which Proposition 2 still holds. The same holds good if one displaces the weight at T onto H and the weight at D into E. The proposition expresses the fact, which is proved for the particular case of Figure 7, that in a balance with three weights it is possible to move each of two equal weights hanging from different arms in opposite directions along the arms, without altering the horizontality of the balance.

At first sight, Proposition 3 seems uninteresting because it concerns only a particular case and is not necessary for the proof of the law of the lever. Its usefulness can be seen from what is written later: in its essence, indeed, it wants to provide a causal justification of the efficiency of a weight on a balance, by introducing the term force of weight to indicate the tendency that a weight has to make the arm of a scale move, recalling to the modern concept of moment of a force; see this significative quotation:

lines and numbers; but the latter are attributes proper to the former. And mechanics too proceeds in the same way.

It is then clear that the diminution of force of weight when the weight is moved from B to T is equal to the diminution that occurs when a weight is moved from T to H. The same reasoning applies to all the quantities of equal lengths taken from CB.

^[193] (p. 225. Translation into English in ^[18])
(M, 3, 1078a)

This statement suggests to generalize Axiom 5’, by removing the clause “hung at one of the two arms”, to become: “If any number of weights keep a balance in the horizontal position, if any two weights are moved along the balance in opposite directions of the same amount, the balance still remains in the horizontal position”.

4. Concluding Remarks

Although this work has the main purpose of illustrating the way in which mathematics was used in ancient Greek mechanics, we believe it appropriate to make some considerations on the merits of the treatment of the law of the lever. In the interpretation provided above of the Mechanica Problemata, one starts from the idea that a force is the more effective the faster the movement of its point of application. In other words, to establish whether the lever is in a state of rest, reference is made to its possible motion, that is, to its kinematics. The formulations of the Hellenistic mathematicians concerning mechanics, of Euclid and Archimedes in primis, do not refer to kinematics; for this, they are labeled as purely static approaches.

Sometimes, it is improperly spoken of the Aristotelian way and the Archimedean way to equilibrium. While the attribution to Archimedes of the purely static approach can be accepted, that to Aristotle is much more problematic. Meanwhile, there are doubts about the attribution, but mainly, the ideas reported therein are very confused. The so-called Aristotelian way is actually the medieval way that was made explicit in the 13th century treatises ^[13]. In the Renaissance, this way was considered not very rigorous by mathematicians with a humanistic background.

Apart from the correct criticism regarding the lack of rigor of medieval treatises, there is also a criticism that lasted at least until the 19th century: what could be the meaning of investigating rest, that is, the absence of motion, by checking what motion is possible? Here is what Bernardino Baldi writes about this:

The power acquires forces from the length of the arm and therefore from the consequent speed; in fact, the longer the arms, the more they are fast at their ends [.].
He was the first to bring mechanics to a system by applying mathematical principles; he also first employed mechanical motion in a geometrical construction, namely, when he tried, by means of a section of a half-cylinder, to find two mean proportionals in order to duplicate the cube. In geometry, too, he was the first to discover the cube, as Plato says in the Republic.

This assertion is certainly true and abundantly substantiated. But we do not agree that the cause of this wonderful effect is the speed resulting from the length of the arm. What speed in fact can an immobile thing have? In fact, the lever and the balance are immobile as long as they are kept in balance and nothing but a small one power bears great weight.

^[235] (p. 126)
(volume 2, book 8, 83, pp. 395–396)

It is worth remarking that Baldi attributed the idea of a dragging effect due to the speed of the moving weight to Aristotle, while such idea is actually difficult to find in the Mechanica problemata. The so-called Aristotelian way to statics began to revive in the 17th and 18th century with Johann Bernoulli and with Lagrange, and in the 19th century, it took on a sufficiently rigorous form accepted by all mathematicians.

References

Merzbach, U.; Boyer, C. A History of Mathematics; Wiley: Hoboken, NJ, USA, 1969.
Heath, T.L. A History of Greek Mathematics: From Aristarchus to Diophantus; Clarendon Press: Oxford, UK, 1921.
Aristotle. Metaphysica; Smith, J.A.; Ross, W.D., Translators; Clarendon Press: Oxford, UK, 1908.
Aristotle. Physica. In The Internet Classical Archive; Hardie, R.P.; Gaye, R.K., Translators; Available online: http://classics.mit.edu/Aristotle/physics.mb.txt (accessed on 27 December 2021).
Laertius, D. Lives of the Eminent Philosophers (2 Vols); Hicks, R.D., Translator; Heinemann: London, UK, 1925.
Aristotle. Mechanical problems. In Aristotle. Minor Works; Hett, W., Ed.; Heinemann: London, UK, 1955.
Abattouy, M. Nutaf Min Al-HiYal: A partial Arabic version of pseudo-Aristotle’s Problemata mechanica. Early Sci. Med. 2001, 6, 96–122.
Rose, P.; Drake, S. The pseudo-Aristotelian questions of mechanics in Renaissance culture. Stud. Renaiss. 1971, 18, 65–104.
Aristotle. Problemi Meccanici; Bottecchia Dheò, M.E., Ed.; Rubbettino: Catanzaro, Italy, 2000.
Kraft, F. Dynamische und Statische Betrachtungsweise in der Antiken Mechanik; Steiner: Wiesbaden, Germany, 1970.
Winter, T. The Mechanical Problems in the Corpus of Aristotle; University of Nebraska: Lincoln, NE, USA, 2007.
McLaughlin, P. The Question of the Authenticity of the Mechanical Problems. 2013. Available online: https://www.uni-heidelberg.de/md/philsem/personal/mclaughlin_authenticity_2013_2.pdf (accessed on 27 December 2021).
Capecchi, D. History of Virtual Work Laws; Birkhäuser: Milan, Italy, 2012.
Leeuwen, J. The Aristotelian Mechanics. Text and Diagrams; Springer: Cham, Switzerland, 2012.
Baldi, B. Vita di Archimede. In Vite Inedite dei Matematici Italiani Scritte da Bernardino Baldi; Narducci, E., Ed.; Tipografia Delle Scienze Matematiche e Fisiche: Rome, Italy, 1887.
Drake, S.; Drabkin, I.E. Mechanics in Sixteenth-Century Italy; University of Wisconsin Press: Madison, WI, USA, 1969.
Bulmer-Thomas, I.; Murdoch, J. Euclid. In Complete Dictionary of Scientific Biography; Gillispie, C.C., Ed.; Scribner: New York, NY, USA, 1971; Volume 4.
Clagett, M. The Science of Mechanics in the Middle Ages; The University of Wisconsin Press: Madison, WI, USA, 1959.
Woepcke, F. Notice sur des traductions de deux ouvrages perdus d’Euclide. Philos. Trans. R. Soc. Lond. 1851, 18, 217–232.
Archimedes. On the equilibrium of planes. In The Works of Archimedes; Heath, T., Ed.; Dover: New York, NY, USA, 2002.
Renn, J.; Damerow, P.; McLaughlin, P. Aristotle, Archimedes, Euclid, and the origin of mechanics: The perspective of historical epistemology. In Symposium Arquímedes. Fundación Canaria Orotava de Historia de la Ciencia; Montesino-Sirera, J., Ed.; Preprint 239; Max-Planck-Institut für Wissenschaftsgeschichte: Berlin, Germany, 2003; pp. 43–59.
Duhem, P. Études sur Leonard de Vinci (3 Vols); Hermann: Paris, France, 1906.
Baldi, B. Bernardini Baldi Urbinatis Guastallae Abbatis in Mechanica Aristotelis Problemata Exercitationes; Albini: Mainz, Germany, 1621.