Surrogate-Based Optimisation | Encyclopedia MDPI

Surrogate-Based Optimisation: Comparison

Please note this is a comparison between Version 1 by Laurens Bliek and Version 4 by Peter Tang.

Surrogate-based optimisation (SBO) algorithms are a powerful technique that combine machine learning and optimisation to solve expensive optimisation problems. This type of problem appears when dealing with computationally expensive simulators or algorithms. By approximating the expensive part of the optimisation problem with a surrogate, the number of expensive function evaluations can be reduced.

surrogate-based optimisation
surrogate model
sequential model-based optimisation
Bayesian optimisation
Green AI
machine learning
sustainable AI
: surrogate-based optimisation

1. Introduction

While undergoing the climate crisis with no easy global solution in sight, some have turned their attention to Artificial Intelligence (AI) as a key technology in the pathway towards a sustainable future ^[1][2][1,2], causing the rise of new AI initiatives such as Climate Change AI [3] and AI for Good [4]. Though it is unlikely that any one technology will be the solution to one of humanity’s greatest challenges, Machine Learning (ML) in particular is seen as a technique with potentially a large positive impact on the United Nations’ Sustainable Development Goals [5] (SDGs), for example in forecasting extreme weather events, balancing supply and demand of renewable energy systems, designing zero-emission transportation systems, identifying woodlands from satellite data, and fault detection in wind turbines ^{[1][6][7][8][9]}[1,6,7,8,9]. This does not come without cost, however, as it turns out ML is a technology with a substantial carbon footprint ^[2][10][2,10]. This has also been recognised in several sub-fields of ML such as natural language processing [11] and Automated ML [12] (AutoML). However, one sub-field of ML, namely, Surrogate-Based Optimisation (SBO), has not yet achieved similar positive or negative attention, even though it is particularly suitable for reducing energy consumption. In fact, SBO techniques are often especially designed to avoid having to run computationally expensive software. This is done by using an ML model as a surrogate of an expensive part of an optimisation problem.

2. Surrogate-Based Optimisation

Motivated by the need for efficiently solving expensive optimisation problems, SBO algorithms such as efficient global optimisation ^[13][14] and Bayesian optimisation ^[14][15] have been developed. These algorithms make use of ML to guide the search for good solutions. The expensive optimisation problems they are designed for can involve computationally demanding simulators, or problems that depend on the outcome of other ML or optimisation algorithms. The problems are also considered ‘black-box’, meaning that no exact mathematical formulation is available that could be exploited. Examples are designing heat pump systems ^[15][16] and diabetes drug manufacturing ^[16][17]. The expensive part of the optimisation problem is approximated with a surrogate model in order to reduce the number of expensive computations. The surrogate model is obtained using ML on the available data of the expensive optimisation problem, and is typically updated during the optimisation process as more data becomes available; see Figure 1. The surrogate model is used inside the optimisation process, which makes SBO a powerful combination of ML and optimisation. A recent textbook introduction to SBO can be found in chapter 10 of ^[17][18].

Figure 1. Simplified framework of a typical SBO algorithm. Optimisation is applied to the surrogate model instead of the expensive simulator or algorithm, giving a candidate solution. This solution is evaluated by the simulator or algorithm. The resulting outcome is given to the surrogate model to be updated using machine learning, making it more accurate over time. This gives better candidate solutions and therefore better outcomes.

As there are many synonyms of ‘surrogate model’ to be found in the literature, such as ‘response surface model’ or ‘metamodel’, and many related terms as well, such as ‘sequential model-based optimisation’, ‘Bayesian optimisation’, or ‘AutoML’, it should come as no surprise that an exact definition of SBO is lacking. This work assumes the following broad definition:

Definition 1.

Surrogate-based optimisation (SBO) is an optimisation technique that makes use of a surrogate model obtained using machine learning, usually to replace an expensive part of the optimisation problem.

Note that this definition makes no distinction between iterative and non-iterative methods, or between surrogate-based and surrogate-assisted methods. The corresponding optimisation problem is given as

where $f : R^{d} \to R^{m}$ :Rd→Rm consists of m objectives that are the outcome of an expensive simulator or algorithm, $x \in R^{d}$ ∈Rd consists of the decision variables, and $X \subseteq R^{d}$ ⊆Rd consists of the search space for the decision variables, including any constraints.

The expensive part of the optimisation Equation (1), which is usually f itself, is approximated with a machine learning model g, called the surrogate model. This is done using the outcomes obtained so far:

where L is a loss function such as the mean squared error or negative log-likelihood, and n is the current iteration of the SBO algorithm. Common surrogate models are Gaussian Processes ^[14][15] and random forests ^[18][19], among others. The surrogate model g is used to provide a candidate solution by finding the maximum of a so-called acquisition function $α$ :

This problem is much easier to solve than the original Equation (1) due to g having a closed form that is easy to evaluate; therefore, traditional optimisation methods such as derivative-based methods can be used. The acquisition function α is used to balance the trade-off between exploration and exploitation. Example acquisition functions are Expected Improvement, Upper Confidence Bound, Thompson sampling, and Entropy Search ^[14][19][15,20]. While the details of SBO algorithms can differ, they all contain a learning part as in (2) and an optimisation part as in (3).

3. Sustainability and Surrogate-Based Optimisation

This section proposes three definitions concerning the intersection of sustainability and SBO. Together, they are called Sustainable SBO (SSBO). Following the terminology of [2], where the distinction is made between AI for Sustainability, i.e., using AI as a tool to achieve sustainability, and Sustainability of AI, i.e., taking carbon footprints and energy consumption into account when developing AI methods, one can define similar notions for SSBO:

Definition 2.

SBO for sustainability is concerned with applying SBO to sustainable applications, for example those that work towards the United Nations SDGs.

Definition 3.

Sustainability of SBO is concerned with making sure the SBO algorithm itself is sustainable, e.g., does not significantly contribute to greenhouse gas emissions, has low energy consumption, is transparent about its computation costs, etc. This holds for both the ML part and the optimisation part of SBO.

However, unlike in AI or ML in general, SBO is concerned with another aspect related to sustainability. As SBO is often used to prevent the prohibitive costs of running computationally expensive simulators multiple times, these ‘savings’ can be considered part of SSBO as well. The following definition is used in this work, where the name Sustainability with SBO is chosen to stay in line with the existing terminology:

Definition 4.

Sustainability with SBO is concerned with the prevention of running computationally expensive software, such as simulators or algorithms, more times than necessary.

‘More times than necessary’ is ill-defined here, but a comparison can be made with any method that would be used if SBO algorithms did not exist, for example randomly searching for good outcomes of a simulator or algorithm, or applying other black-box optimisation techniques that do not make use of ML surrogates, e.g., metaheuristic algorithms.

It is this last aspect of SBO that sets it apart from other AI techniques, as the main goal of SBO is to reduce the number of expensive function evaluations for some objective function. In fact, Definition 4 is the actual purpose for which SBO has been developed in the first place, starting with algorithms such as EGO for expensive black-box optimisation ^[13][14]. At the same time, such types of ‘energy savings’ that are the result of using less expensive function evaluations, must be considered carefully when compared to the other SSBO definitions, so as to prevent falling into the trap of Jevons’ paradox ^[20][21]. This paradox, when translated to the case of SSBO, could counter-intuitively result in using SBO with the same or an even higher number of function evaluations than any other algorithm because it is so efficient, which results in no savings of computational resources.

All in all, the three SSBO definitions must be carefully weighed against each other, similar to the weighing of sustainable AI notions according to Wynsberghe [2]: “to assess whether training or tuning of an AI model for a particular task is proportional to the carbon footprint, and general environmental impact, of that training and/or tuning”. While such a ‘proportionality framework’ [2] is beyond the scope of this paper, Definition 2 is the main focus of this research, though the other SSBO definitions get some attention as well.

4. Surrogate-Based Optimisation for Sustainable Applications

4.1. Year

Due to the search terms used in this survey, all years are covered in full: the year 2022 is not over at the time of writing this paper, but this year was not included in the survey. The number of studies included in this survey increased from 2 in 2017, to 4 in 2018, 8 in 2019, 14 in 2020, and finally 17 in 2021. Even though there is room for other search queries than the one used in this work, and therefore quantitative results could be subject to bias, this does give the indication that interest in applying SBO to sustainable applications has increased over the surveyed time period. A potential explanation for this is that both sustainability and AI were popular topics in this time period, not only in public but also in private sectors. Looking at AI investments for example: “From 2015 to 2020, the total yearly corporate global investment in AI increased by 55 billion U.S. dollars” ^[21][32]. It is likely that research on SBO, as a subset of AI, has benefited from this popularity. At the same time, the surveyed period closely follows the adoption of the Paris Agreement ^[22][33] and the United Nations SDGs [5], which have likely had a significant impact on the research focus of the time period under consideration.

4.2. Framework

While SBO methods such as Bayesian optimisation typically use an iterative approach, where surrogate models are constantly updated and used to search for better candidate solutions, this was not the only framework in which surrogate models found here were used. Non-iterative or direct approaches were more common, probably due to not including terms like ‘Bayesian optimisation’ or ‘sequential model-based optimisation’ in the search query.

4.3. Surrogate Model

The type of surrogate model used in the included studies varied a lot, mostly depending on the framework. Artificial Neural Networks (ANNs) are very popular in PtO, while Gaussian Processes (GPs) or Radial Basis Functions (RBFs) are more common in other frameworks such as SMBO or BlO. As noted in one of the included studies ^[23][52], the popularity of ANNs can likely be explained by the success of deep learning in the last decade and by researchers having access to more powerful hardware that allows more complex models. Other surrogate models were Multivariate Adaptive Regression Spline (MARS), Support Vector Machine (SVM) or Support Vector Regression (SVR), linear and polynomial regression, piece-wise linear models, Random Forest (RF), Recurrent Neural Network (RNN), and ensembles of multiple models. A general explanation of how to use ML models such as ANNs or GPs in SBO can be found in, e.g., ^[17][18].

4.4. Application and Domain

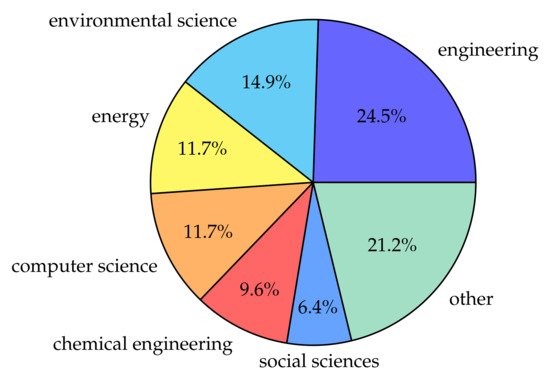
The range of applications is quite broad, from groundwater management to electric vehicles. The terms in the ‘application’ column of Table 1 were chosen manually after reading the studies, and might be subject to bias, especially considering the broad range of topics. Therefore, the domains of the application are also mentioned: these are retrieved from SCOPUS directly. A broad list of domains is covered, but engineering, environmental science, energy and computer science were the most common domains, covering over half of all included studies as seen in Figure 2. While the prominence of energy and environmental science is to be expected when searching for sustainability-related studies, the engineering domain is likely well-represented due to SBO being considered a subset of engineering optimisation ^[17][18]. Similarly, SBO is considered part of AI, which can be considered part of the computer science domain.

Figure 2.

Domains of the studies encountered in this literature survey.

Table 1. Properties of the surveyed literature. SSBO = Sustainable Surrogate-Based Optimisation, SMBO = Sequential Model-Based Optimisation, PtO = Predict then Optimise, OtP = Optimise then Predict, PtI = Predict then Interact, BlO = Bi-level Optimisation, AutoML = Automated Machine Learning.

Study	Year	Framework	Surrogate	Application	Domain	SSBO	Open Questions
^[24][62]	2017	PtO	MARS	groundwater extraction	engineering	✓	parallelisation
^[25][44]	2017	PtO	ANN	aviation	engineering	✓	dimension reduction
^[26][38]	2018	PtO	ANN	food production	chemical engineering; computer science	-	assumptions
^[27][42]	2018	BlO	unknown	land development	chemical engineering; computer science	-	-
^[28][55]	2018	SMBO	ANN	production systems	chemical engineering; chemistry	✓	sustainability in objective
^[29][63]	2018	PtO	SVR	groundwater extraction	environmental science; earth and planetary sciences	-	hyperparameter optimization
^[30][64]	2019	PtO	SVR	groundwater extraction	environmental science; social sciences	-	-
^[31][39]	2019	OtP	polynomial, RBF, GP	electric vehicles	energy; engineering	-	high dimensionality
^[32][47]	2019	PtO	polynomial	outdoor thermal comfort	social sciences; engineering	-	many objectives
^[33][65]	2019	PtO	GP	thermal comfort	environmental science	-	-
^[34][36]	2019	review	multiple	building design	engineering	✓	high dimensionality; smoothness; efficiency; interpretability
^[35][66]	2019	PtO	SVR	groundwater management	environmental science	-	multiple objectives
^[16][17]	2019	SMBO	RBF	drug manufacturing	chemical engineering; chemistry; energy; environmental science	-	multiple objectives
^[36][51]	2019	OtP	ANN	building renovation	engineering	✓	generalisation; efficient sampling
^[37][67]	2020	BlO	ANN	water management	environmental science	-	multiple and fuzzy objectives
^[38][48]	2020	PtO	ANN	solar heat system	energy; engineering; environmental science; business, management and accounting	-	-
^[23][52]	2020	review	multiple	building design	engineering	-	incorporate behavioural data; reproducibility
^[39][40]	2020	PtI	RF; ensemble ANN	building design	engineering	-	multiple objectives; multiple users
^[40][41]	2020	PtI; PtO	RF	building design	social sciences; computer science; arts and humanities	✓	multiple users
^[41][68]	2020	SMBO	GP	sea transport	engineering; computer science	-	parallelisation
^[42][35]	2020	SMBO	ANN	water management	environmental science; engineering	-	many objectives
^[43][69]	2020	OtP	linear	cooling tower	engineering; environmental science	-	-
^[44][70]	2020	PtO	ANN	building energy management	engineering	-	efficiency
[45]	2020	PtO	ANN	air conditioning	energy	-	transfer learning
^[46][54]	2020	SMBO	GP	material discovery	chemical engineering; materials science	-	include historic data
^[47][71]	2020	SMBO	polynomial	public transport	mathematics; computer science	-	complex variable interactions; visualisation
^[48][72]	2020	review	multiple	hydro-cracking	energy; environmental science; social sciences	✓	multidisciplinarity
^[49][73]	2020	BlO	RBF; GP; polynomial	transportation networks	engineering; social sciences; decision sciences	-	hyperparameter optimisation; model selection
^[50][74]	2021	PtO	linear; SVM	product design	engineering; chemical engineering	-	robustness
^[51][46]	2021	PtO	multiple	urban logistics	mathematics; computer science	✓	robustness
^[52][75]	2021	review; PtO	multiple	process design; material design	chemical engineering; computer science; energy; engineering; environmental science; materials science	✓	high dimensionality; generalisation
^[53]^[54][30,31]	2021	PtO	ANN	building design	energy; materials science	✓	high dimensionality and constraints
^[55][53]	2021	SMBO	RBF	soil health	agriculture and biological sciences; computer science	✓	variable reduction
^[56][49]	2021	SMBO	ANN	hydropower reservoir	engineering; computer science	-	high dimensionality; parallelisation
^[57][50]	2021	BlO	RBF	electric vehicles	business, management and accounting; engineering; social sciences	✓	mixed variables and constraints
^[58][56]	2021	SMBO	GP ensemble	chemical process	business, management and accounting; energy; engineering; environmental science	✓	high dimensionality; multimodality
^[59][43]	2021	AutoML	RBF; GP	groundwater management	computer science; decision sciences; mathematics	✓	generalisation
^[60][76]	2021	PtO	ANN	urban drainage systems	environmental science	✓	divide problem into subproblems
^[61][77]	2021	PtO	RNN	bridge maintenance	business, management and accounting; engineering	-	-
^[62][78]	2021	PtO	ANN	chemical process	chemical engineering; chemistry; engineering	-	robustness
^[63][79]	2021	PtO	RBF ensemble	concrete barriers	computer science; engineering; mathematics	-	-
^[64][80]	2021	PtO	ANN	water management	energy	-	multiple objectives; accuracy
^[15][16]	2021	SMBO	RBF	heat pump system	energy	-	multiple objectives; constraints; robustness; discrete variables
^[65][81]	2021	PtO	ANN	thermal comfort	engineering	✓	generalisation
^[66][82]	2021	PtO	piece-wise linear	agricultural system	energy; chemistry; chemical engineering; environmental science	✓	high dimensionality; nonlinearity; nonconvexity

4.5. Sustainable SBO

As explained in Section 3, this work considers three types of Sustainable SBO (SSBO). SBO for Sustainability is about the sustainability aspects of the application itself. This work assumes that all the included studies cover this aspect in some way or another: e.g., ^[55][53] uses SBO to increase soil health by 7.6%, while ^[46][54] finds several new stable chemical compounds for sustainable energy applications using SBO. This assumption is made in order to reduce bias, and because of the wide range of applications which requires expertise in many different science domains to fully understand the sustainability aspects of the applications. The corresponding column in Table 1 ignores this aspect of SSBO and only reveals whether other SSBO aspects were covered. This was done by manually inspecting the studies and is therefore still subject to bias, so only examples and general insights are given here.

Sustainability with SBO is about the prevention of running computationally intensive simulators or algorithms. Since this is the main reason for using SBO, it is assumed that all included studies take this aspect into account when choosing their methods. However, most studies do not quantify this aspect, which makes it difficult to determine whether the benefits (SBO for Sustainability and Sustainability with SBO) are worth the computational resources of SBO itself (Sustainability of SBO). An example of an included study that does quantify this is ^[28][55], where the total time of the SBO approach was estimated at 15 h for evaluating the expensive simulator and 1 000 s for the ML and optimisation parts of the SBO approach, while directly optimising the expensive simulator using the same optimisation procedure without a surrogate model was estimated to take 330 h. In other words, SBO has lead to approximately a 95% reduction in computational resources for this application, when compared to other optimisation techniques that do not make use of ML. Similar savings in computation time were reported for sustainable building design in one of the included reviews ^[34][36], with 97% as the largest reported number. Studies that quantify this aspect of SSBO get a checkmark in the corresponding column in Table 1.

Finally, studies that discuss Sustainability of SBO itself, for example by mentioning the trade-off in computational resources between expensive optimisation problem and SBO framework, or by quantifying the computation time or energy usage of their SBO framework, get a checkmark in the corresponding column. An example is ^[25][44], where computation times for training the ANN surrogate, using the surrogate for optimisation, and evaluating the expensive simulator are all reported. The study estimates that the surrogate model is 4000 times faster than the expensive simulator after performing the ‘predict’ step of the PtO framework. If the entire PtO framework is taken into account, the study estimates that the SBO framework is more efficient than a regular optimisation framework (in this case the gradient descent or Nelder–Mead simplex algorithm) in the situation that the expensive simulator is called more than 168,000 times. The authors conclude that “the use of ANN in multidisciplinary optimization frameworks transfers the computational cost of the aircraft optimization task to the ANN training process”.

It should be noted that the above study was an exception: almost none of the studies included in this work mentioned this last aspect of SSBO, i.e., the computational resources of the SBO framework. What was usually mentioned is the number of samples used to train the surrogate model, but not the time used to train or optimise the surrogate. In some studies, computation times of the SBO framework were reported in the supplementary material, e.g., ^[53][30]. In others, such as ^[58][56], the ML and optimisation parts of the SBO framework were considered to be negligible, so only the total computation time of using the SBO framework and evaluating the expensive simulator together were mentioned. While it is indeed the case for many applications that the SBO framework has negligible computation time compared to the expensive simulator, this is certainly not the case for all applications, as seen with the study ^[25][44] earlier. Therefore, it is important to keep track of both the computation time of the SBO framework itself and the computation time spent on calling the expensive simulator, and to separate these.