Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 3 by Norherdawati Kasim and Version 9 by Amina Yu.
Non-sieving mechanism is a particle removal process in which particles smaller than the membrane pores are captured by adsorption at the pore surface. The non-sieving mechanism plays an important role for charged solute. There are three accepted non-sieving mechanisms: Donnan exclusion, dielectric exclusion, and hydration mechanism.
- nanofiltration
- size exclusion
- Donnan exclusion
- membrane separation
1. Non-Sieving Mechanism
Non-sieving mechanism is a particle removal process in which particles smaller than the membrane pores are captured by adsorption at the pore surface. NF membrane is considered unique as it lies between non-porous RO membranes (where transport is governed by a solution-diffusion mechanism) and porous UF membranes (where separation occurs as a result of size exclusion and charge effects) [1]. The non-sieving mechanism plays an important role for charged solute. As mentioned earlier, the Nernst–Planck model has been used to investigate the steric effect between uncharged solutes. Geraldes and Alves introduced NanoFiltran, an open-source program for modeling transport of multi-ionic solutions through NF membranes based on the extended Nernst–Planck equation [2]. The results show that NanoFiltran is a valuable tool for accurate and robust prediction of the mass transfer in nanofiltration of multi-ionic solutions. Next, Epsztein et al. [3] incorporated NanoFiltran in their work investigating the role of ionic charge density on Donnan exclusion (a non-sieving mechanism). A brief analysis of open-source codes has included in this paper as Supplementary Data.
It has been concluded that NF membrane has a complicated exclusion mechanism, which involves combining both sieving and non-sieving mechanisms. Supporting evidence of this statement can be found in various studies that have concluded that steric hindrance plays a predominant role in the rejection mechanism and that electrostatic effect also has a significant role during the separation process of TrOCs [4][5][6][7]. In addition, T. Fujioka et al. [8] compared the ceramic membrane and polymeric NF membrane by evaluating the rejection of TrOCs. The researchers determined that hydrophobicity influenced the interaction between TrOCs and the polymeric NF membrane during the rejection process, suggesting additional rejection mechanisms other than size exclusion. To the best of our knowledge, there are three accepted non-sieving mechanisms: Donnan exclusion, dielectric exclusion, and hydration mechanism. Donnan exclusion and dielectric exclusion mechanisms are illustrated in Figure 1. ThisFigure 1 figure briefly explains both sieving (steric exclusion) and non-sieving mechanisms (Donnan exclusion and dielectric exclusion).

Figure 1. Schematic representation of solute exclusion mechanisms in nanofiltration as per the Donnan steric pore model with dielectric exclusion (DSPM–DE). Reprinted with permission from Yagnaseni Roy, David M. Warsinger, John H. Lienhard (2017). Copyright 2021 Copyright Elsevier [9].
1.1. Donnan Exclusion
Donnan exclusion occurs when ions partition into a material that contains high density of charge [10]. NF membrane is mainly governed by Donnan exclusion and size exclusion [11]. Emamjomeh et al. [12] also determined that the separation mechanism in NF membrane mainly involved the size of the molecules and the electrical response between the surface of the membrane and the ions in the feed. Furthermore, Donnan exclusion occurs due to electrostatic interactions between ionic solutes and the membrane matrix’s fixed electric charges [13]. Based on these claims from various researchers, one can conclude that NF membrane rejection is not solely determined by the size exclusion; it is also determined by Donnan exclusion. Figure 2 illustrates how Donnan exclusion works for both negatively and positively charged membranes. Negatively charged membranes reject negative ions (yellow ball) but allow positive ions (red ball) to pass through the membrane by transport of various solutes and entraps some of the ions in between the channel pore of the membrane. Solutes are transported by diffusion (movement of solute down a concentration gradient), by convection (solute transported by bulk fluid motion), and by electromigration (ion movement due to the membrane potential gradient [9]. The same law is depicted in reverse in Figure 2b.
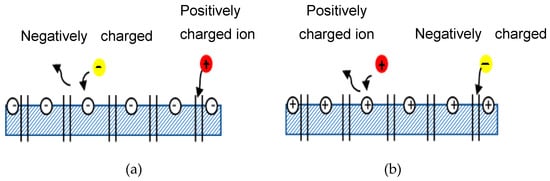
Figure 2. Schematic diagram of Donnan exclusion. (a) Negatively charged membrane, (b) Positively charged membrane.
To investigate the role of Donnan exclusion in the removal of arsenic by nanofiltration, Seidel et al. [14] evaluated surface charge, pore size, and rejection behaviour for salt solutions such as sodium chloride (NaCl), calcium chloride (CaCl2), and sodium sulphate (Na2SO4). They determined that the order of rejection rate for these salts is Na2SO4 > NaCl > CaCl2. These findings are consistent with Donnan exclusion. According to Donnan exclusion principle, the rejection of ions increases with co-ions that have higher charges and decreases with counter-ions that have higher charges. Na2SO4 has the highest rejection rate because it contains co-ions with the greatest negative charge, which is sulphate (SO42−) ions. Simultaneously, CaCl2 has the lowest rejection since it has higher charge of counterions which is calcium (Ca2+). The rejection trends shown in their study demonstrate that the ion separation is governed by size exclusion and Donnan exclusion, as the observed trends do not correspond to the size of the hydrated ions.
Donnan exclusion is also more pronounced on divalent ions [15][16]. Nicolini and colleagues evaluated the performance of NF membrane by measuring the saline rejection. The saline rejection for the NF membrane decreases in the following sequence: Na2SO4 > K2SO4 > CaSO4 > MgSO4 > NaCl. The saline rejection sequence is a result of anionic electrostatic repulsion and the preferred attraction of divalent cations.
Furthermore, the performance of fabricated polyamide (PA) NF membranes via interfacial polymerisation using m-xylylenediamine (m-XDA) and polyethyleneimine (PEI) as aqueous monomers were evaluated [16]. Liu and co-researchers controlled the concentration ratio of m-XDA and PEI from 1:0, 4:1, 3:2, 2:3, and 1:4 to 0:1 and named them M1, M2, M3, M4, M5, and M6. The researchers also investigated the selectivity of Na+ and Mg2+. The results showed that the addition of PEI to aqueous solution increased the rejection of NF membrane to magnesium chloride (MgCl2) and magnesium sulphate (MgSO4), but not to NaCl or Na2SO4. This is because both MgSO4 and MgCl2 have divalent cations (Mg2+), while NaCl and Na2SO4 only have monovalent cations (Na+). Therefore, Mg2+ rejection is determined by Donnan exclusion, whereas monovalent Na+ rejection is determined by steric hindrance (since Na+ has weak electrostatic repulsion).
However, the Donnan exclusion mechanism is not sufficiently explained only by the rejection of ionic solutes. A model is needed to describe the rejection of ions by NF membranes. Consequently, a model to calculate ion rejection in single and mixed electrolyte solutions in RO and NF membranes has been proposed [17]. The researchers designed the model based on the extended Nernst–Plank equation and combined it with Teorell–Meyer–Sievers (TMS) model [18]. Bowen and Mukhtar proposed in 1996 that an ideal quantitative model for membrane processes should consider the physical properties of the membrane to predict separation behaviour under specified conditions [19]. The physical properties of the membranes that have been utilized are effective membrane thickness and charge density. They used a hybrid model (HM), which was initially developed for glomerular filtration and incorporated the extended Nernst–Planck equation and Donnan partitioning between the solution and membrane [20]. Next, in 1997, a new model called the Donnan steric pore model (DSPM) based on the hybrid model was developed by Bowen et al. [21]. This model has been widely used and evaluated because it describes Donnan exclusion sufficiently. For example, Donnan exclusion was used to predict the movement of ions (containing Ca2+, K+, and Cl−) through a negatively charged membrane.
Schaep et al. evaluated the DSPM model using four commercial NF membranes to investigate the influences of molecular size, polarity, and charge on the retention of organic molecules. The researchers also evaluated the selected membrane with single-species salt solutions such as NaCl, Na2SO4, MgCl2, and MgSO4 [22]. The results showed that the membrane charge density was inconsistent and depended solely on salt type and concentration. Furthermore, due to divalent cations in the feed solution, the agreement between DSPM fitting and actual results was less than adequate. The model predicted an unreasonably high membrane charge density, and the presence of divalent cations changed the sign of the membrane charge density from negative to positive [23]. As a result, dielectric exclusion (DE) is used here as a secondary partitioning effect at the membrane-external solution interfaces, which will be discussed in greater detail in the following section.
1.2. Dielectric Exclusion
As mentioned in a previous section, it has been determined that there is an additional separation mechanism due to the unrealistic magnitude of membrane charge density predicted by DSPM. Therefore, Yaroshcuk et al. [24] introduced dielectric exclusion during the separation process by providing an in-depth analysis of this exclusion mechanism. The researchers stated that dielectric exclusion occurs when an ion interacts with the bound electrical charges generated by the ion at the interface of two materials with different dielectric constants: in this case, the membrane matrix and the solvent. It was determined that the ion polarizes the two media in accordance with their relative dielectric constants, forming a polarisation charge distribution at the discontinuity surface. This phenomenon is called as production of image forces and is illustrated in Figure 3. This figure shows that if the membrane's dielectric constant is less than the solvent's, this image force will always be repulsive for both anions and cations.
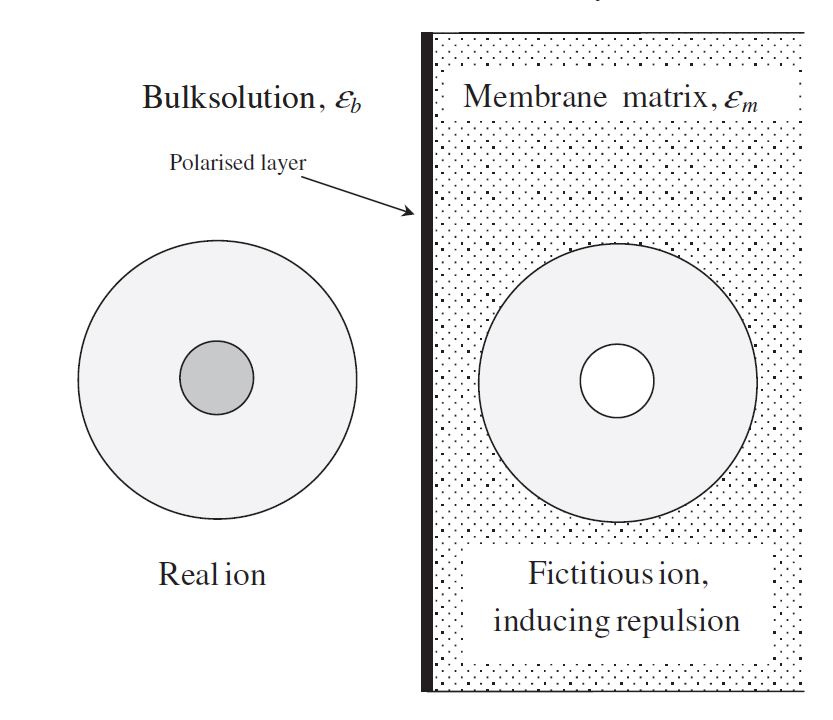
Figure 3. An ionic species approaching the NF membrane surface induces a repulsive image force.
In addition, Bowen and Welfoot widened the scope of the DSPM by incorporating more complex phenomena into their latest model [25]. Their study compared the effects of the solvent viscosity and the dielectric constant inside the pore. The results showed that variation of the solvent was insignificant, but the variation of the dielectric constant inside the pore was significant. It is believed that when the dielectric constant inside the pores decreases, it becomes smaller than the dielectric exclusion of bulk solution. Therefore, changes of the dielectric constant in the pores induced an excess energy barrier for ion solvation, preventing charged ions from partitioning into the pores. The effect was named dielectric exclusion (DE) and a Born equation was proposed to quantify it (Born effect). The researchers discovered that the dielectric effect reduced the charge density (extracted from experimental data) to a more reasonable number and improved model fitting when divalent salts were used. By incorporating the dielectric effect into the DSPM, this model is referred to as the Donnan steric pore model with dielectric exclusion (DSPM–DE) model. More recently, this model has been used widely by various researchers [26][27][28][29]. One of the highlighted studies explored the effect of dielectric constant in NF membrane [30]. The results showed that when the dielectric constant is decreased, the rejection performance is increased. As depicted in Figure 43, the dielectric constant was lowered from 80 to 60 and the rejection performance was increased as dielectric constant decreased. Therefore, it can be concluded that the dielectric constant holds an important role in the rejection performance of NF membrane.
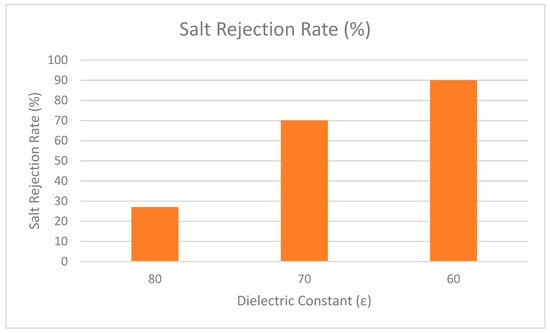
Figure 43.
Rejection performance of salt at different dielectric constant.
However, in practice, the DSPM–DE model is inconsistent because dielectric effects are based on slit-like pores, while the transport model is based on cylindrical pores. Later, Szymczyk and Fievet (2005) developed a steric, electric, and dielectric exclusion (SEDE) model. The researchers utilized both effects of dielectric exclusion mechanisms, which are the Born effect and image forces contribution [31]. The researchers stated that the SEDE model can be used to predict transport via cylindrical or slit-shaped pores. Later that year, Bouranene et al. [32] studied whether dielectric exclusion should be represented by the Born effect, the image force, or both. The modelling findings demonstrate that the experimental rejection rates are not adequately characterised when the two types of dielectric exclusion mechanisms are included. Hence, the researchers stated that the DSPM–DE developed by Bowen et al. (2002) was adequate for practical applications. Furthermore, as mentioned by Wang, researchers have made many modifications for various scenarios. However, the original DSPM–DE framework remains the most often utilized due to its capabilities of fitting experimental data in most cases [23].
1.3. Hydration Mechanism
As stated by Yaroshcuk, the hydration mechanism is not well understood [13]. It has been proposed that a loss of water dissolving capability of the membrane is likely caused by the changes to the dielectric properties of that particular membrane. The researcher also mentioned that multiple-charged ions should be considerably better excluded from the pores than single-charged ions which are sodium (Na+) and potassium ion (K+) [33]. Chen et al. concluded that the rejection of Na+ is higher even though K+ has a smaller hydration radius than Na+. This is because the diffusion coefficient of K+ calculated using Stokes’ law and Zwanzig’s theory is larger than that of Na+. Furthermore, the relationship between water molecules and hydrated cations passing through the graphene oxide (GO) membrane in a temperature-assisted system was studied [34]. Cha-umpong and others studied temperature-assisted systems as the driving force instead of pressure-assisted systems since theoretically, temperature as the driving force should not compromise salt rejection.
The researchers discussed why the rejection of Ca2+ is stronger than Mg2+ in terms of hydration radius. The first hydration radius of Ca2+ is bigger than that of Mg2+. The unique feature of divalent ions is their structure, as two layers of hydration shell surround the ions. The first layer is dense while the second layer (outer layer) is elastic, and this layer weakly connects with nuclear ions. If ions have a radius larger than the pore size, the ions can still pass through the pore because the water molecules adjust its outer hydration shell so that the inner hydration shell can pass through the pore. Figure 5 explains the mechanism of ions passing through the pore despite having a larger radius than the pore. Figure 5 displays several water molecules from the outer hydration shell being replaced and resulting the first hydration shell can easily pass through the pore. After passing through the pore, the second hydration shell will attract some other water molecules in the permeated region to form a new hydration shell.
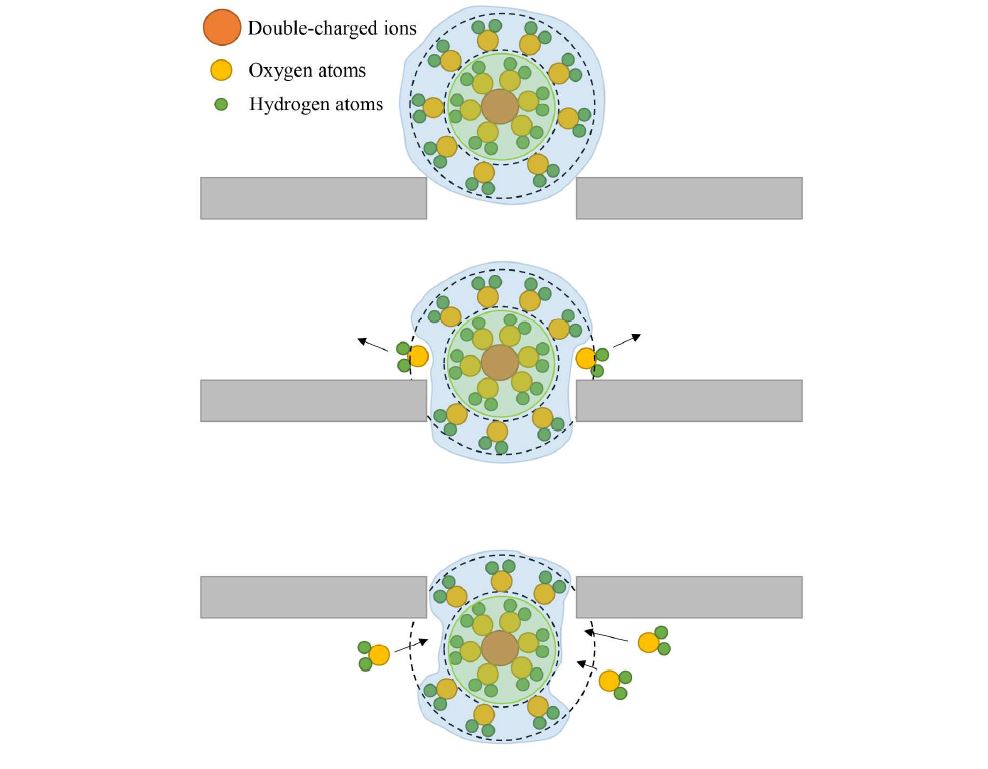
Figure 5. The schematic diagram of ions that have larger radius passing through the pore.
2. Donnan Exclusion as the Main Non-Sieving Rejection Mechanism
Nanofiltration membrane can be considered to have a negative charge on its surface. This was verified in a study done by Macnaughton et al. [35], who determined that most of the nanofiltration membranes are negatively charged at a neutral pH. The researchers stated that one of the factors that determined the surface membrane to be negatively charged or positively charged is the membrane functional group. Negatively charged membranes generally contain sulfonic acid groups (R−S(=O)2−OH), while positively charged membranes contain amine (−NH2) or imine groups. By changing the functional groups of the membrane, we can enhance the membrane selectivity. Hence, many researchers have devoted studies to fabricating NF membranes with tuning the charges on or in the selective layer to enhance the selectivity processes. Table 1 provides a summary of recent studies concerning the role of the surface charge of membrane.
Table 1. List of published studies regarding NF membrane and their results for the rejection of salt.
| Membrane Charged | Results | Refs. | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NF-2012-250, polyamide thin-film composite membranes were used for the rejection of high divalent salt | Negative | CaSO4 > Na2SO4 > MgSO4 > MgCl2 > NaCl | [36] | |||||||||||||||
| Chitosan (CTS) and 1,3,5-triglycidyl isocyanurate (TGIC) were gradiently cross-linked on the polyethersulfone ultrafiltration membrane (PES) |
Positive | MgCl | 2 | > MgSO | 4 | > NaCl > Na | 2 | SO | 4 | [37] | ||||||||
| Polyamide (PA) nanofiltration membranes with high solute-solute selectivity were prepared via a pre-diffusion interfacial polymerization (PDIP) process |
Negative | Na | 2 | SO | 4 | > MgSO | 4 | > MgCl | 2 | > CaCl | 2 | > NaCl | [38] | |||||
| Poly (vinyl alcohol) (PVA)/polydopamine (PDA) hybrid nanofiltration membrane was fabricated through aqueous electrospraying |
Negative | Na | 2 | SO | 4 | > MgSO | 4 | > NaCl | [39] | |||||||||
| A polyvinyl chloride (PVC)-based nanofiltration membrane was fabricated from polyvinyl chloride- | graft | -poly( | N | , | N | -dimethylaminoethyl methacrylate) by heating and crosslinking treatment |
Positive | MgCl | 2 | > CaCl | 2 | > NaCl > MgSO | 4 | > Na | 2 | SO | 4 | [40] |
| Nanofiltration membranes were prepared by polydopamine (PDA) deposition followed by crosslinking on the polyethersulfone (PES) ultrafiltration (UF) membrane substrate. |
Positive | MgCl | 2 | > CaCl | 2 | > NaCl > MgSO | 4 | > Na | 2 | SO | 4 | [41] | ||||||
| A membrane was fabricated via introducing 2, 5 diaminobenzenesulfonic acid (DABSA) into the polyamide layer | Negative | Na | 2 | SO | 4 | > MgSO | 4 | > NaCl > MgCl | 2 | [42] | ||||||||
| Polyamide (PA) thin film composite (TFC) membranes were prepared by interfacial polymerisation (IP) technique with trimesoyl chloride (TMC) and three acyl chloride groups |
Negative | MgSO | 4 | > Na | 2 | SO | 4 | > MgCl | 2 | > NaCl | [43] | |||||||
| Thermally cross-linked branched-polyethyleneimine (b-PEI) layer was introduced to a loose polyethersulfone NF membrane by dip-coating b-PEI and an epoxy linker and heat treatment in a sealed oven with a high-humidity atmosphere | Positive | MgCl | 2 | > | MgSO | 4 | > | NaCl | > | Na | 2 | SO | 4 | [44] |
In Table 12, it can be seen that the rejection of salt for both negatively and positively charged membranes were mainly governed by Donnan exclusion mechanism. As discussed in Section 4.1, if the NF membrane is negatively charged, the rejection is increased for co-ions that have higher negative charge. Hence, the results for the rejection of salt by the negatively charged NF membrane in the constructed table were almost the same. The order of the rejection is Na2SO4 > MgSO4 > MgCl2 > CaCl2 > NaCl. The rejection of Na2SO4 is higher than that of MgSO4 even though both salts consist of sulphate (SO42−) ions, which are the co-ions with the greatest negative charge. This is because Na2SO4 has the counter-ions with the lowest positive charge, sodium (Na+) ions, unlike MgSO4, which has magnesium (Mg2+) ions. The rejection is followed by MgCl2 since the salt consists of chloride (Cl−) ions.
For the positively charged NF membrane, the order of the rejection of salt is MgCl2 > MgSO4 > NaCl > Na2SO4. As stated earlier, the principle of Donnan exclusion is that rejection increases if the salt consists of greatest charge of co-ions and smallest charge of counter ions. Since the membranes were positively charged, the co-ions were cations and the counter-ions were anions. Based on the order MgCl2 > MgSO4 > NaCl > Na2SO4, the rejection of MgCl2 was higher than that of MgSO4 since chloride (Cl−) ions are smaller than sulphate (SO42−) ions. This principle also applies to NaCl and Na2SO4. Hence, it can be concluded that Donnan exclusion is the main non-sieving rejection mechanism in the charge status of the membranes.
References
- Shon, H.K.; Phuntsho, S.; Chaudhary, D.S.; Vigneswaran, S.; Cho, J. Nanofiltration for water and wastewater treatment—A mini review. Drink. Water Eng. Sci. 2013, 6, 47–53.
- Geraldes, V.; Brites Alves, A.M. Computer program for simulation of mass transport in nanofiltration membranes. J. Membr. Sci. 2008, 321, 172–182.
- Epsztein, R.; Shaulsky, E.; Dizge, N.; Warsinger, D.M.; Elimelech, M. Role of Ionic Charge Density in Donnan Exclusion of Monovalent Anions by Nanofiltration. Environ. Sci. Technol. 2018, 52, 4108–4116.
- Bellona, C.; Drewes, J.E.; Xu, P.; Amy, G. Factors affecting the rejection of organic solutes during NF/RO treatment—A literature review. Water Res. 2004, 38, 2795–2809.
- Kong, F.-X.; Yang, H.-W.; Wang, X.-M.; Xie, Y.F. Assessment of the hindered transport model in predicting the rejection of trace organic compounds by nanofiltration. J. Membr. Sci. 2016, 498, 57–66.
- Wang, X.-M.; Li, B.; Zhang, T.; Li, X.-Y. Performance of nanofiltration membrane in rejecting trace organic compounds: Experiment and model prediction. Desalination 2015, 370, 7–16.
- Dong, L.X.; Huang, X.C.; Wang, Z.; Yang, Z.; Wang, X.M.; Tang, C.Y. A thin-film nanocomposite nanofiltration membrane prepared on a support with in situ embedded zeolite nanoparticles. Sep. Purif. Technol. 2016, 166, 230–239.
- Fujioka, T.; Khan, S.J.; McDonald, J.A.; Nghiem, L.D. Nanofiltration of trace organic chemicals: A comparison between ceramic and polymeric membranes. Sep. Purif. Technol. 2014, 136, 258–264.
- Roy, Y.; Warsinger, D.M.; Lienhard, J.H. Effect of temperature on ion transport in nanofiltration membranes: Diffusion, convection and electromigration. Desalination 2017, 420, 241–257.
- Tang, C.; Bruening, M.L. Ion separations with membranes. J. Polym. Sci. 2020, 58, 2831–2856.
- Ng, L.Y.; Mohammad, A.W.; Ng, C.Y. A review on nanofiltration membrane fabrication and modification using polyelectrolytes: Effective ways to develop membrane selective barriers and rejection capability. Adv. Colloid Interface Sci. 2013, 197–198, 85–107.
- Emamjomeh, M.M.; Torabi, H.; Mousazadeh, M.; Alijani, M.H.; Gohari, F. Impact of independent and non-independent parameters on various elements’ rejection by nanofiltration employed in groundwater treatment. Appl. Water Sci. 2019, 9, 71.
- Yaroshcuk, A.E. Rejection mechanisms of NF membranes. Membr. Technol. 1998, 1998, 9–12.
- Seidel, A.; Waypa, J.J.; Elimelech, M. Role of charge (Donnan) exclusion in removal of arsenic from water by a negatively charged porous nanofiltration membrane. Environ. Eng. Sci. 2001, 18, 105–113.
- Nicolini, J.V.; Borges, C.P.; Ferraz, H.C. Selective rejection of ions and correlation with surface properties of nanofiltration membranes. Sep. Purif. Technol. 2016, 171, 238–247.
- Liu, Y.; Lin, B.; Liu, W.; Li, J.; Gao, C.; Pan, Q. Preparation and characterization of a novel nanofiltration membrane with chlorine-tolerant property and good separation performance. RSC Adv. 2018, 8, 36430–36440.
- Tsuru, T.; Nakao, S.-I.; Kimura, S. Calculation of ion rejection by extended nernst-planck Equation with charged reverse osmosis membranes for single and mixed electrolyte solutions. J. Chem. Eng. Jpn. 1991, 24, 511–517.
- Teorell, T. Transport Processes and Electrical Phenomena in Ionic Membranes. Prog. Biophys. Biophys. Chem. 1953, 3, 305–369.
- Bowen, W.R.; Mukhtar, H. Characterisation and prediction of separation performance of nanofiltration membranes. J. Membr. Sci. 1996, 112, 263–274.
- Deen, W.M.; Satvat, B.; Jamieson, J.M. Theoretical model for glomerular filtration of charged solutes. Am. J. Physiol. 1980, 7, 126–139.
- Bowen, W.R.; Mohammad, A.W.; Hilal, N. Characterisation of nanofiltration membranes for predictive purposes—Use of salts, uncharged solutes and atomic force microscopy. J. Membr. Sci. 1997, 126, 91–105.
- Van Der Bruggen, B.; Schaep, J.; Wilms, D.; Vandecasteele, C. Influence of molecular size, polarity and charge on the retention of organic molecules by nanofiltration. J. Membr. Sci. 1999, 156, 29–41.
- Wang, R.; Lin, S. Pore model for nanofiltration: History, theoretical framework, key predictions, limitations, and prospects. J. Membr. Sci. 2021, 620, 118809.
- Yaroshchuk, A.E. Dielectric exclusion of ions from membranes. Adv. Colloid Interface Sci. 2000, 85, 193–230.
- Bowen, W.R.; Welfoot, J.S. Modelling the performance of membrane nanofiltration-critical assessment and model development. Chem. Eng. Sci. 2002, 57, 1121–1137.
- Fadaei, F.; Hoshyargar, V.; Shirazian, S.; Ashrafizadeh, S.N. Mass transfer simulation of ion separation by nanofiltration considering electrical and dielectrical effects. Desalination 2012, 284, 316–323.
- Roy, Y.; Sharqawy, M.H.; Lienhard, J.H. Modeling of flat-sheet and spiral-wound nanofiltration configurations and its application in seawater nanofiltration. J. Membr. Sci. 2015, 493, 360–372.
- Ghorbani, A.; Bayati, B.; Drioli, E.; Macedonio, F.; Kikhavani, T.; Frappa, M. Modeling of nanofiltration process using dspm-de model for purification of amine solution. Membranes 2021, 11, 230.
- Deepak, D.; Arthanareeswaran, G. Modeling and Performance Characteristics of Nanofiltration by DSPM and ARX Model. J. Appl. Membr. Sci. Technol. 2017, 18, 1–7.
- Zhu, Y.; Zhu, H.; Li, G.; Mai, Z.; Gu, Y. The effect of dielectric exclusion on the rejection performance of inhomogeneously charged polyamide nanofiltration membranes. J. Nanopart. Res. 2019, 21, 217.
- Szymczyk, A.; Fievet, P. Investigating transport properties of nanofiltration membranes by means of a steric, electric and dielectric exclusion model. J. Membr. Sci. 2005, 252, 77–88.
- Saliha, B.; Patrick, F.; Anthony, S. Investigating nanofiltration of multi-ionic solutions using the steric, electric and dielectric exclusion model. Chem. Eng. Sci. 2009, 64, 3789–3798.
- Chen, B.; Jiang, H.; Liu, X.; Hu, X. Molecular Insight into Water Desalination across Multilayer Graphene Oxide Membranes. ACS Appl. Mater. Interfaces 2017, 9, 22826–22836.
- Cha-Umpong, W.; Hosseini, E.; Razmjou, A.; Zakertabrizi, M.; Korayem, A.H.; Chen, V. New molecular understanding of hydrated ion trapping mechanism during thermally-driven desalination by pervaporation using GO membrane. J. Membr. Sci. 2020, 598, 117687.
- MacNaughton, S.J.; McCulloch, J.K.; Marshall, K.; Ring, R.J. Application of nanofiltration to the treatment of uranium mill effluents. In Technologies for the Treatment of Effluents from Uranium Mines, Mills and Tailings, Proceedings of a Technical Committee Meeting, Vienna, Austria, 1–4 November 1999; IAEA: Vienna, Austria, 2002; pp. 55–65.
- Ali, M.E.A. Nanofiltration process for enhanced treatment of RO brine discharge. Membranes 2021, 11, 212.
- Yang, B.; Gu, K.; Wang, S.; Yi, Z.; Zhou, Y.; Gao, C. Chitosan nanofiltration membranes with gradient cross-linking and improved mechanical performance for the removal of divalent salts and heavy metal ions. Desalination 2021, 516, 115200.
- Zhang, L.; Zhang, R.; Ji, M.; Lu, Y.; Zhu, Y.; Jin, J. Polyamide nanofiltration membrane with high mono/divalent salt selectivity via pre-diffusion interfacial polymerization. J. Membr. Sci. 2021, 636, 119478.
- Geng, X.; Wang, J.; Ding, Y.; Zhang, W.; Wang, Y.; Liu, F. Poly(vinyl alcohol)/polydopamine hybrid nanofiltration membrane fabricated through aqueous electrospraying with excellent antifouling and chlorine resistance. J. Membr. Sci. 2021, 632, 119385.
- Fang, L.F.; Zhou, M.Y.; Cheng, L.; Zhu, B.K.; Matsuyama, H.; Zhao, S. Positively charged nanofiltration membrane based on cross-linked polyvinyl chloride copolymer. J. Membr. Sci. 2019, 572, 28–37.
- Mi, Z.; Liu, Z.; Jin, S.; Zhang, D.; Wang, D. Positively charged nanofiltration membrane prepared by polydopamine deposition followed by crosslinking for high efficiency cation separation. Polym. Test. 2021, 93, 107000.
- Wei, X.Z.; Gan, Z.Q.; Shen, Y.J.; Qiu, Z.L.; Fang, L.F.; Zhu, B.K. Negatively-charged nanofiltration membrane and its hexavalent chromium removal performance. J. Colloid Interface Sci. 2019, 553, 475–483.
- Tian, J.; Chang, H.; Gao, S.; Zhang, R. How to fabricate a negatively charged NF membrane for heavy metal removal via the interfacial polymerization between PIP and TMC? Desalination 2020, 491, 114499.
- Yun, T.; Kwak, S.Y. Recovery of hydrochloric acid using positively-charged nanofiltration membrane with selective acid permeability and acid resistance. J. Environ. Manag. 2020, 260, 110001.
More
