Coverage Path Planning Methods Focusing on Energy Efficient: Comparison
View Latest Version
Please note this is a comparison between Version 3 by Rita Xu and Version 2 by Georgios Fevgas.

The coverage path planning (CPP) algorithms aim to cover the total area of interest with minimum overlapping. The goal of the CPP algorithms is to minimize the total covering path and execution time. Significant research has been done in robotics, particularly for multi-unmanned unmanned aerial vehicles (UAVs) cooperation and energy efficiency in CPP problems. This paper presents a review of the early-stage CPP methods in the robotics field. Furthermore, we discuss multi-UAV CPP strategies and focus on energy-saving CPP algorithms. Likewise, we aim to present a comparison between energy-efficient CPP algorithms and directions for future research.

  • coverage path planning
  • unmanned aerial vehicle
  • cell decomposition
  • decomposition methods
  • energy-aware approaches
  • energy optimal path
  • multi-robot systems
  • multi-UAV

1. Introduction

In recent years, due to rapid technological development, UAVs and sensors they can carry have been developed to the extent that they can cover a wide range of applications [1] that cannot be satisfied by other types of robots [2]. Some of the applications are precision agriculture [3[3][4],4], search and rescue [5], firefighting [6], law enforcement [7], powerline inspection [8], oil and gas [9], disaster management [10], and cell network expansion [11]. However, a fundamental problem is the optimal use of autonomous aircraft in terms of time and space [2].
Recently, CPP algorithms have been developed, considering the parameters required for more efficient data retrieval from remote sensing sensors [12,13][12][13]. In addition, algorithms have been developed that use multi-UAV to cover the area, thus reducing the coverage time of the area of interest [14,15][14][15]. The way to cover an area with autonomous robots differs depending on the algorithm [2,16,17][2][16][17]. In the literature, CPP algorithms use different methods (e.g., grids, graphs, and neural networks) with calculations performed online or offline for known or unknown areas [18].
The CPP algorithms can be classified into two main categories: offline and online [19]. Offline algorithms need to know the environment and the information included, such as obstacles and the geometry of the area of interest. Of course, in a real-life environment, many dynamic parameters cannot be known in advance. Offline algorithms have prior knowledge of the coverage area environment [20]. They also provide more efficient and convenient route plans and use less central processing unit (CPU) power than online algorithms [21].
The online algorithms are based on real-time environment data retrieved from onboard sensors to cover the area of interest. Online algorithms do not fully understand the coverage area environment, and the coverage path is executed in real-time by the UAV after processing the data using the sensors it carries. The benefits of online algorithms are the design of the in-flight route to complete the mission regardless of unforeseen situations and the unnecessary prior detailed knowledge of the coverage area [20,22][20][22].
Furthermore, there are two categories of problems in area coverage: single coverage and repeat coverage. The goal of single coverage is to cover the entire area of interest and, at the same time, minimize the time and distance traveled by the coverage route [23]. On the other hand, repetitive coverage aims to repeatedly cover all points of interest in the area, maximize the frequency of visits to points of interest, and minimize time and total coverage [24].

2. Methods

For t

2. No Decomposition

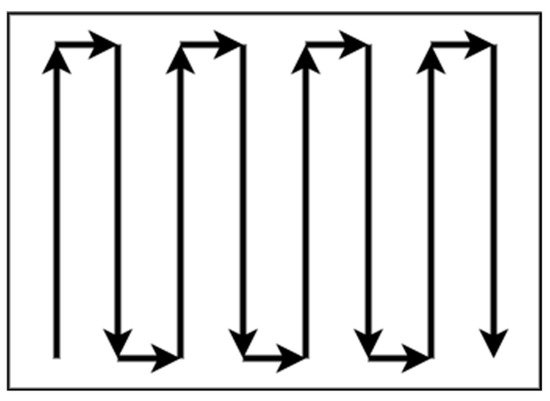
The present work, a systematic review research methodology was adopted. In that context, a range of platforms was sourced for information. Most of the sources cited in this survey were found in (a) the IEEE Xplore digital library, (b) the Google scholar platform, (c) the online Elsevier platform, and is no need for decomposition in areas with regular shapes and without complexity, such as rectangular areas. Patterns with simple path planning, such as boustrophedon or square, are adequate for total coverage of a non-complex area without overlapping. The boustrophedon method, which means “the way of the ox,” is a pattern of simple back and forth motion along the longest side of the polygon, as shown in d)Figure 1 t[25][26][27].
Sensors 22 01235 g001 550
Figure 1. Boustrophedon pattern.
The online MDPI platform. Kterature assumeywords utilized were: “Coverage Path Planning”, “Decomposition methods”, “CPPthat the actual path is closely true to the plan when this methods”, “Multi-robot CPP methods”, “Cell decomposition”, “Unmanned Aerial Vehicles”, “Energy optimal path”, “Energy-aware approaches”, “Multi-robot systems”, “Robot coverage”, “Robot kine is executed from a ground vehicle. On the other hand, UAVs are aerodynamically directly affected by the direction and intensity of the wind, which means that the actual trajectory of the flight in most cases is not close to that planned.
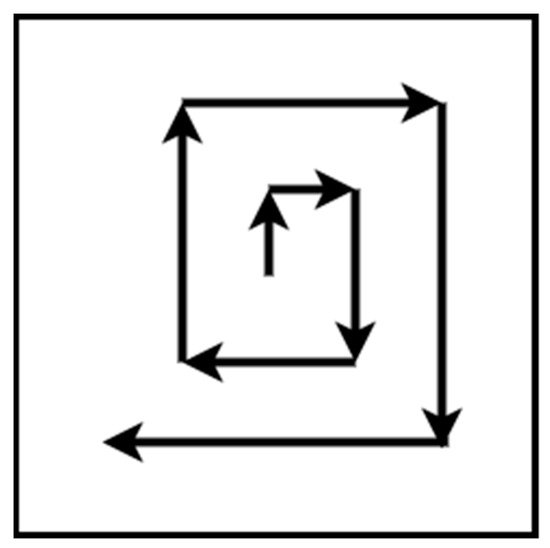
The square maetics”hod is represented by Andersen [28], and “UAVit is a Remote Sensing”. Initially, the resulting papers (approximately 170) were filtered by choosingpattern for a search and rescue mission. The flight path is straight lines with right 90 degrees turns. The pattern starts from the center of the area of interest and expands until the borders, as shown in tFigure 2.
Sensors 22 01235 g002 550
Figure 2. Square pattern.

3. Exact Cellular Decomposition

The cellular decones referring to CPP algorithms,mposition methods are based on dividing an irregular space into cells. One class of these methods is the exact one. The exact cellular decomposition methods, multi-robotd decomposes the irregular space into cells, and multi-UAV coverage path strategies, and energy-awareness CPP algorithmstheir connections produce an accurate free space composition. Accurate methods are complete because they guarantee the finding of an accessible path, if any [29]. The 170 sub-aforementioned publications reviewed forreas that arise from the decomposition methods,n can be covered from a single UAV or multi-robot CPP strategies, multi-UAV CPP methods, and UAV energy-saving algorithms. From the 170 papers, 128 were classified according to thple UAVs. There are patterns for a single UAV, such as boustrophedon and spiral for polygon and concave areas. Nevertheless, there are strategies for the cooperation of multiple UAVs in order to minimize the coverage time [30].

4. Trapezoidal Decomposition

One exact cellular decomposition technique for irregular spaces that can give a complete coverage path is trapezoidal decomposition. This method is classified in the offline category of algorithms because it does not use remote-sensing information [31][32]. Each cell is a trapezoid in this method, and simple methods such as back and forth can be used to cover every cell. The coverage can be achieved by an exhaustive walk that generates a path to cover each cell to execute the path using back and forth motions such as boustrophedon, as shown in Figure 3. Often, this method is used for agriculture applications where the fields are polygonal and clear from obstacles. Oksanen and Visala [33] introduced an algorithm for CPP in agricultural fields and used the path cost function to optimize the final path.

Sensors 22 01235 g003 550
Figure 3. Trapezoidal decomposition.

5. Boustrophedon Decomposition

Trapelevance of the survey’s scope and their overlapping information. In the end, 128 papers were analyzed for their approaches and their correlation to categorize in sub-sectionzoidal decomposition produces many cells, some of which can be merged. This characteristic is a disadvantage because as many cells exist, the coverage path will be longer. To overcome this limitation, a method that creates nonconvex cells is needed. The boustrophedon cellular decomposition is similar to trapezoidal decomposition but considers vertices in the area called critical points [25][27]. The bofustrophedon decomposition methods, CPP methods, and energy-saving algorithm, of reduces the number of cells compared with trapezoidal decomposition, which 88 made it into means shorter path planning, as shown in Figure 4. As the trefined versionapezoidal decomposition, this method is for polygonal areas, and the environment of the present surveycoverage area should be known.

3. Results

C For thoiset [19] reason, it can be classified theas CPP algorithms accordian offline method.
Sensors 22 01235 g004 550
Figure 4. Boustrophedon decomposition.

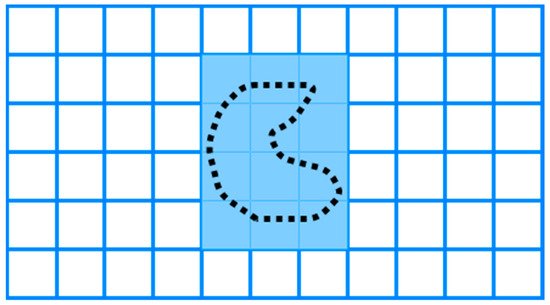
6. Morse-Based Decomposition

Ang to the ther cellular decomposition usedmethod proposed by Acar et al. [34] is based on Morste functions CPP[35]. The algMorithmsse-based decompose the area of interest in cells. This method is preferable forition method has the advantage of different cells shapes such as circular and can be applied in any dimensional space, such as concave, polygon, and irregular areas. On the other hand, whenspace. The cell decomposition is succeeded with a slice that sweeps through the area of interest is a regular shape, it does not require any decomposition for single coverage of UAV. Table 1 a. A slice is discontinued at the critical point of the Morse function, which is restricted from the the end ofobstacle boundaries, as shown in Figure 5. tThis section summarizes the decomposition method uses information concerning the area during motion planning. For this reason, the methods and can be classified as online [36][37].
Sensors 22 01235 g005 550
Figure 5. Morse-based decomposition.

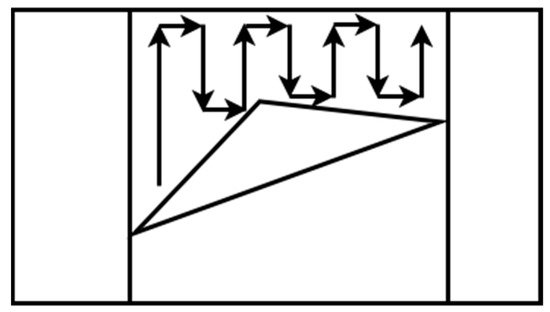
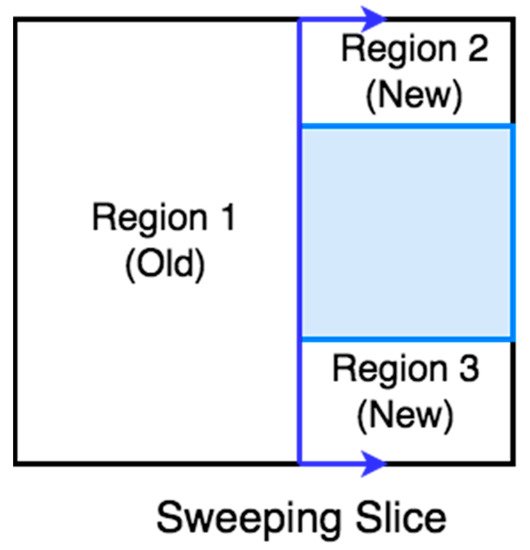
7. Online Topological Coverage Algorithm

Wong [38] presented an algorithm that finds the CPP approach, thcell boundaries online using slice decomposition. Slice decomposition is a method, the algorithm processing, the shape of for determining the cell boundaries using a sweeping line over the area of interest, and the corresponding reference.

3.1. No Decomposition

There is no need for decomposition in areas with regular shapes and without complexity, such as rectangular areas. Patterns with simple path planning, such as boustrophedon or square, are adequate for total coverage of a non-complex area without overlapping. The boustrophedon method, which means “the way of the ox,” is a pattern of simple back and forth motion along the longest side of the polygon, as shown in
. As the line sweeps over the area, it separates the obstacles and free space in two regions or more, as shown in
Figure 1 [33,34,35].
6. The algorithm constructs a topological map using the slice decomposition on the area of interest [39].
Sensors 22 01235 g006 550
Figure 16. BoustrophSlicedon patter decomposition.
The literature assumes that the actual path is closely true to the plan when this method is executed from a ground vehicle. On the other hand, UAVs are aerodynamically directly affected by the direction and intensity of the wind, which means that the actual trajectory of the flight in most cases is not close to that planned.
The square method is represented by Andersen [36], and it is a pattern for a search and rescue mission. The flight path is straight lines with right 90 degrees turns. The pattern starts from the center of the area of interest and expands until the borders, as shown in Figure 2.
Sensors 22 01235 g002 550
Figure 2. Square pattern.

3.2. Exact Cellular Decomposition

The cellular decomposition methods are based on dividing an irregular space into cells. One class of these methods is the exact one. The exact cellular decomposition method decomposes the irregular space into cells, and their connections produce an accurate free space composition. Accurate methods are complete because they guarantee the finding of an accessible path, if any [37]. The sub-areas that arise from the decomposition can be covered from a single UAV or multiple UAVs. There are patterns for a single UAV, such as boustrophedon and spiral for polygon and concave areas. Nevertheless, there are strategies for the cooperation of multiple UAVs in order to minimize the coverage time [38].

3.3. Trapezoidal Decomposition

O

8. Contact Sensor-Based Coverage of Rectilinear Environments

Butler et al. [40] present ane exact cellular decomposition technique for irregular spaces that can give a complete coveragealgorithm for contact sensor-based robots for online coverage of the rectilinear environment. In contact sensor-based coverage, the robot’s path is cycling with retracing, while at the same time it repeatedly constructs a cellular decomposition of the area of interest. When a robot’s full-cycle path is unsuccessful, it chooses a new path is trapezoidabased on its position and environment. The robot’s motion depends on the area’s cell decomposition. Th state, updated as the CPP progresses.

9. Grid-Based Methods

Grid-based method iss are classified in the offline category of algorithms bec as approximate cellular decomposition due to the restriction of the grid’s shape, which is uniform in space. It is impossible to represent precisely the shape of the target space and its obstacles [19]. The grid-bause it does not use remote-sensingd methods decomposed the space into uniform grid cells, which can be squares or other shapes, as shown in Figure 7. Moravec ianfd Elfes [41] proposed a grmation [39,40].id map presentation based on a Esonach cell is a trapezoid inr mounted on a mobile robot mapping an indoor environment.
Sensors 22 01235 g007 550
Figure 7. Grid-based decomposition.

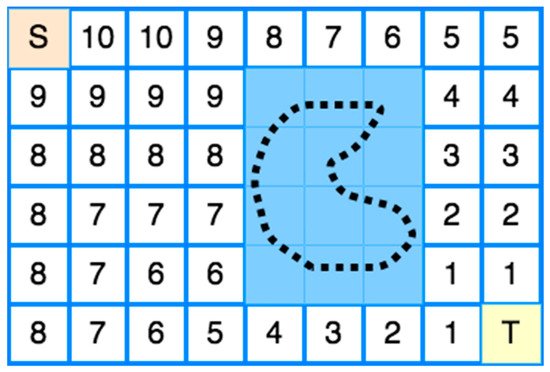
9.1. Wavefront Algorithm

The firsthis CPP’s grid-based method, and simpl was proposed by Zelinsky et al. [42]. Their methods such as back and forth can be used to cover every has a start cell and a goal cell. A grid represents the coverage area, and a wavefront algorithm is used from the goal cell to the start cell. The coverage can be achieved by an exhaustive walk that geneIts operation is based on propagating a “wavefront” from the target cell passing through the free cells and bypassing all obstacles to the starting cell.
Morates a path to cover each specifically, the transmission of the “wavefront” from the target cell to execute the path using back and forth motions such as boustrophedonthe starting cell is used to assign specific numbers to each cell of the grid, as shown in Figure 38. OfFirsten, this method is used for agriculture applications where the fields are polygonal and clear from obstacles. Oksanen and Visala [41]ly, 0 is assigned to the target cell and then 1 to all adjacent cells. Then, all the other adjacent cells of 1 to which no number has been assigned are assigned 2. The intproduced an algorithm for CPP in agriculturalcess repeats incrementally until the wavefront reaches the starting point [13][20]. The fenvields and used the path cost function to optimize the final pathronment should be known in this method, so the method can be classified offline.
Sensors 22 01235 g003 550
Figure 3. Trapezoidal decomposition.

3.4. Boustrophedon Decomposition

Trapezoidal decomposition produces many cells, some of which can be merged. This characteristic is a disadvantage because as many cells exist, the coverage path will be longer. To overcome this limitation, a method that creates nonconvex cells is needed. The boustrophedon cellular decomposition is similar to trapezoidal decomposition but considers vertices in the area called critical points [33,35]. The boustrophedon decomposition reduces the number of cells compared with trapezoidal decomposition, which means shorter path planning, as shown in Figure 4. As the trapezoidal decomposition, this method is for polygonal areas, and the environment of the coverage area should be known. For this reason, it can be classified as an offline method.
Sensors 22 01235 g004 550
Figure 4. Boustrophedon decomposition.

3.5. Morse-Based Decomposition

Another cellular decomposition method proposed by Acar et al. [42] is based on Morse functions [43]. The Morse-based decomposition method has the advantage of different cells shapes such as circular and can be applied in any dimensional space, such as concave, polygon, and irregular space. The cell decomposition is succeeded with a slice that sweeps through the area of interest. A slice is discontinued at the critical point of the Morse function, which is restricted from the obstacle boundaries, as shown in Figure 5. This method uses information concerning the area during motion planning. For this reason, the method can be classified as online [44,45].
Sensors 22 01235 g005 550
Figure 5. Morse-based decomposition.

3.6. Online Topological Coverage Algorithm

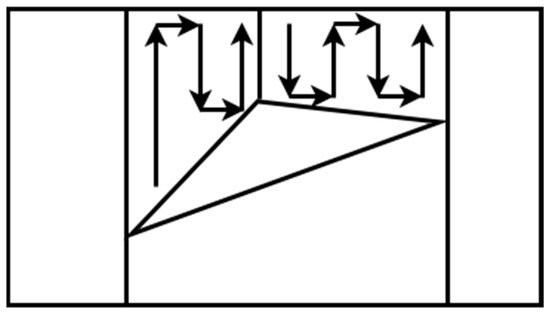
Wong [46] presented an algorithm that finds the cell boundaries online using slice decomposition. Slice decomposition is a method for determining the cell boundaries using a sweeping line over the area of interest. As the line sweeps over the area, it separates the obstacles and free space in two regions or more, as shown in Figure 6. The algorithm constructs a topological map using the slice decomposition on the area of interest [47].
Sensors 22 01235 g006 550
Figure 6. Slice decomposition.

3.7. Contact Sensor-Based Coverage of Rectilinear Environments

Butler et al. [48] present an exact cell decomposition algorithm for contact sensor-based robots for online coverage of the rectilinear environment. In contact sensor-based coverage, the robot’s path is cycling with retracing, while at the same time it repeatedly constructs a cellular decomposition of the area of interest. When a robot’s full-cycle path is unsuccessful, it chooses a new path based on its position and environment. The robot’s motion depends on the area’s cell decomposition state, updated as the CPP progresses.

3.8. Grid-Based Methods

Grid-based methods are classified as approximate cellular decomposition due to the restriction of the grid’s shape, which is uniform in space. It is impossible to represent precisely the shape of the target space and its obstacles [19]. The grid-based methods decomposed the space into uniform grid cells, which can be squares or other shapes, as shown in Figure 7. Moravec and Elfes [49] proposed a grid map presentation based on a sonar mounted on a mobile robot mapping an indoor environment.
Sensors 22 01235 g007 550
Figure 7. Grid-based decomposition.

3.8.1 Wavefront Algorithm

The first CPP’s grid-based method was proposed by Zelinsky et al. [50]. Their method has a start cell and a goal cell. A grid represents the coverage area, and a wavefront algorithm is used from the goal cell to the start cell. Its operation is based on propagating a “wavefront” from the target cell passing through the free cells and bypassing all obstacles to the starting cell.
More specifically, the transmission of the “wavefront” from the target cell to the starting cell is used to assign specific numbers to each cell of the grid, as shown in Figure 8. Firstly, 0 is assigned to the target cell and then 1 to all adjacent cells. Then, all the other adjacent cells of 1 to which no number has been assigned are assigned 2. The process repeats incrementally until the wavefront reaches the starting point [13,20]. The environment should be known in this method, so the method can be classified offline.
Sensors 22 01235 g008 550
Figure 8. Wavefront Transmission from starting cell (S) to target cell (T).
Nevertheless, Shivashankar et al. [51] proposed a wavefront algorithm to accomplish an online CPP with a mobile robot in an unknown spatial environment.
Nevertheless, Shivashankar et al. [43] proposed a wavefront algorithm to accomplish an online CPP with a mobile robot in an unknown spatial environment.

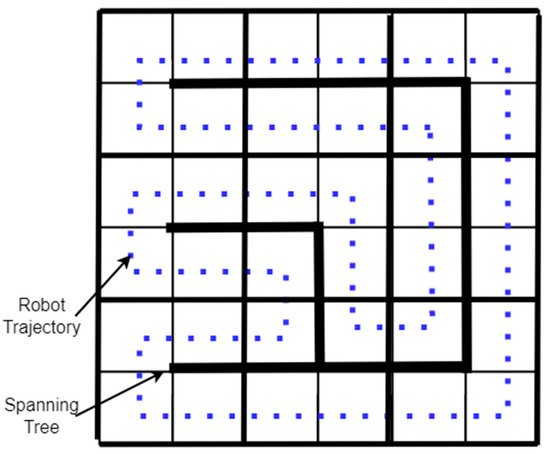
3.8.2 Spanning Tree Coverage

9.2. Spanning Tree Coverage

The spanning tree coverage (STC) algorithm solves the problem of covering an area using a robot [38]. The method used by the STC algorithm is first to decompose the region into cells and calculate a connecting tree of the resulting graph. Finally, the robot’s path starts near the “connecting tree” and follows its perimeter, as shown in
The spanning tree coverage (STC) algorithm solves the problem of covering an area using a robot [30]. The method used by the STC algorithm is first to decompose the region into cells and calculate a connecting tree of the resulting graph. Finally, the robot’s path starts near the “connecting tree” and follows its perimeter, as shown in
Figure 9 [37]. A Spiral-STC algorithm was proposed by Gabriely and Rimon [52]. This online method converts the space into a grid map. The mobile robots execute a spanning tree-generated spiral path using onboard sensors.
[29]. A Spiral-STC algorithm was proposed by Gabriely and Rimon [44]. This online method converts the space into a grid map. The mobile robots execute a spanning tree-generated spiral path using onboard sensors.
Sensors 22 01235 g009 550
Figure 9. Spanning Tree-based coverage.

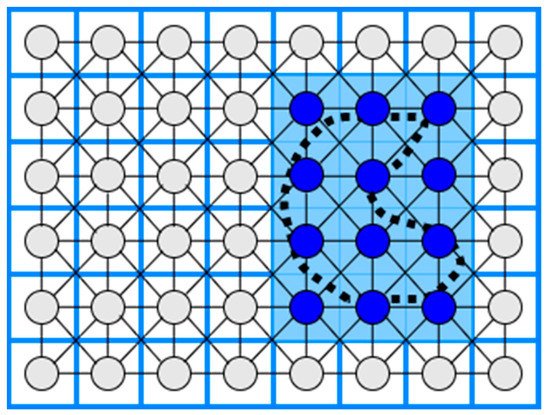
3.9. Neural Network-Based Coverage on Grid Maps

10. Neural Network-Based Coverage on Grid Maps

The CPP using a neural network is an online coverage method. First, in a 2D coverage area, a grid map is constructed where the length of the diagonal of each cell is equal to the coverage radius of the robot (e.g., the coverage radius of a robotic broom), and then a neuron is associated with each cell in the grid. Each neuron is connected to the eight primary neighboring neurons, as shown in
Figure 10. Finally, the robot’s path to the coverage area is executed by knowing each output value of each neuron at a given time, so that the robot is attracted to cells it has not visited while at the same time being rejected by cells it has visited [53,54].
. Finally, the robot’s path to the coverage area is executed by knowing each output value of each neuron at a given time, so that the robot is attracted to cells it has not visited while at the same time being rejected by cells it has visited [45][46].
Table 1. CPP and decomposition methods.
CPP Approach Decomposition Method Algorithm Processing Shape of Area Reference
Boustrophedon None Offline Rectangular [33,34,35][25][26][27]
Square None Offline Square [36][28]
Boustrophedon, Spiral Exact cellular Offline Polygon, Concave [37][29]
Back and Forth Trapezoidal Offline Polygon [39,40][31][32]
Boustrophedon Boustrophedon Offline Polygon [33,35][25][27]
Boustrophedon Morse-based Online Any dimensional [42][34]
Online Topological Slice Online Polygon [46][38]
Contact Sensor-based Exact cellular Online Rectilinear [48][40]
Wavefront Approximate cellular Offline Polygon, Concave [50][42]
Wavefront Approximate cellular Online Polygon, Concave [51][43]
STC Approximate cellular Offline Polygon, Concave [37][29]
Spiral-STC Approximate cellular Online Polygon, Concave [52][44]
Neural Network-based Approximate cellular Online Polygon, Concave [53,54][45][46]
Sensors 22 01235 g010 550
Figure 10. Neural Network-based coverage.

11. Multi-Robot CPP Strategies

3.10. Multi-Robot CPP Strategies

Multiple robots have an advantage over single robotic systems [24]. The use of multiple robots accelerates coverage of an area of interest. The problem of covering an area with multiple robots lies in the calculation of optimal routes in order to minimize the coverage time [38]. Using multiple robots in a CPP work reduces the completion time due to workload division [20]. This section discusses multi-robot coverage methods based on single robot approaches, multi-robot strategies, and multiple UAVs to cover an area of interest. Some drawbacks of multiple UAV strategies are spatial orientation and communication difficulties. Table 2 at the end of this section summarizes the multi-robot CPP strategies and presents the CPP approach, the decomposition method, the algorithm processing, and the corresponding reference.

3.11. Multi-Robot Boustrophedon Decomposition

Rekleitis et al. [16] presented a set of online algorithms for solving the CPP using a group of mobile robots in an unknown environment. The algorithms employ the same planar cellular decomposition as the Boustrophedon single robot coverage algorithm, with additions to manage how robots cover a single cell and distribute among cells. Their solution takes into account the team members’ communication limitations. The robots serve two roles to accomplish coverage where some members, known as explorers, cover the boundaries of the actual target cell, while others, known as coverers, conduct basic back-and-forth motions to cover the cell.

3.12. Multi-Robot Spanning Tree Coverage

Their experimental data reveal that their technique outperforms multi-robot spanning tree coverage (MSTC) by a significant margin. Nevertheless, the coverage time of an area with the multi-robot forest coverage (MFC) algorithm is shorter than the MSTC algorithm [38]. Moreover, an online, robust version of MSTC was provided by Hazon et al. [55]. They show that the approach is robust analytically, providing as much coverage as a single robot can.

3.13. Multi-Robot Neural Network-Based Coverage

A neural network approach for multi-robot coverage where each robot sees all the others as obstacles and the avoidance ability of stalemate situations was proposed by Luo and Yang [54,56,57]. The multi-robot neural-network based coverage is inspired by single robot neural-network coverage. During the coverage of the irregular-shaped area of interest, the robots see each other as moving obstacles.

3.14. Multi-Robot Graph-Based and Boundary Coverage

Easton and Burdick [58] presented a two-dimensional boundary coverage method for multiple robots. A team of robots must inspect all points on the boundary of the two-dimensional target environment, and each robot’s inspection routes are planned to use a heuristic search. The planned paths cover the entire boundary. Moreover, the algorithm has been validated by simulations. The multi-robot boundary coverage is inspired by the need to inspect the blade surfaces inside a turbine.
Table 2. Multi-robot CPP strategies.
CPP ApproachDecomposition MethodAlgorithm ProcessingReference
BoustrophedonExact cellularOnline[16]
Spanning Tree CoverageApproximate cellularOnline[55]
Neural network-basedApproximate cellularOnline[54,56,57]
Graph-based and BoundaryApproximate cellularOffline[58]

3.15. Multi-UAV CPP Methods

The number of applications where UAVs can be used is increasing as remote-sensing technology is developed. In the literature, there are a lot of multi-UAV CPP methods using different coverage algorithms with heterogeneous or homogeneous UAVs that were used in a variety of applications, such as agriculture [59], surveillance [60], mapping [61], and search and rescue missions [62]. Table 3 at the end of this section summarizes the multi-UAV CPP strategies and presents the CPP approach, the type of UAVs, the algorithm processing, the evaluation metrics, and the corresponding reference.

3.16. Multi-UAV Coverage

In the agricultural sector, Barrientos et al. [13] proposed a method for area coverage using a fleet of mini aerial robots. Their method divides the area of interest in k non-overlapping subtasks and assigns them in k UAVs. A decentralized method for surveillance missions using homogeneous UAVs was proposed by Acevedo et al. [63]. This method’s primary goal is to minimize latency, which means a short sharing time of information between the UAVs. In a later work, Acevedo et al. [64] developed a method for surveillance in urban environments with heterogeneous UAVs that fly at low altitudes and avoid obstacles. Finally, in their most recent work, Acevedo et al. [65] developed a method based on grid-shape area partition, which can readjust the area shape and UAVs’ capacity.
A terrain coverage method using a fleet of heterogeneous UAVs was presented by Maza and Ollero [61]. Their method divides the irregular-shaped area of interest per each UAV capability, such as total flight time. Each partition is assigned to a UAV that plans a zig-zag covering pattern according to the area’s characteristics to minimize the number of turns. The method was validated in simulation.
A coverage algorithm for fixed-wing UAVs with the ability for obstacle and previously scanned regions avoidance was presented by Xu et al. [23,66]. Their method uses boustrophedon cellular decomposition [33], an exact cellular decomposition, and presents better accuracy than trapezoidal decomposition. The method can be classified as online in the phase of region scanning and offline in the coverage phase.

3.17. Back-and-Forth

Maza and Ollero [61] present a cooperative technique using heterogeneous UAVs in a convex polygonal area. A ground control station divides the area into sub-regions and assigns them to every UAV by the capability and starting position. Every UAV calculates back-and-forth patterns according to the camera footprint to reduce the number of turns.

3.18. Spiral

Balampanis et al. [67,68] present a spiral CPP algorithm using multiple heterogeneous UAVs. The area of interest is divided according to UAVs sensing capabilities using a constrained Delaunay triangulation (CDT) [69]. The CDT generates triangle cells that match almost exactly the shape of the area of interest. To make the triangles more uniform, they applied Lloyd optimization [70]. Then, a spiral algorithm generates the coverage pattern for each sub-area. This method can generate smoother trajectories considering avoiding no-fly zones and the shape of the coverage area. However, it generates more extensive coverage paths and a higher number of turns than classical grid decomposition and motion methods [71,72].

3.19. Multi-Objective Path Planning (MOPP) with Genetic Algorithm (GA)

Hayat et al. [73] propose multi-objective path planning (MOPP) with a genetic algorithm (GA) for search and rescue missions using multiple UAVs. The mission is divided into two phases: search and response. The search phase monitors an event to guarantee the total coverage in a given area, and the response phase spreads detection updates on the network. The MOPP algorithm performs the planning task during the search, while the GA minimizes the mission completion time. As a result, the method can be classified as offline in the search phase and online in the response phase.

3.20. Genetic Algorithm (GA) with Flood Fill Algorithm

Based on the Trujillo et al. [74] approach, Darrah et al. [75] present a CPP method for missions over more extensive areas using multi-UAVs. The method produces equitable sub-areas of the area of interest to cover by multi-UAVs or several flights performed by a single UAV. The flood fill algorithm integrated with game theory was applied to partition the area of interest. Each UAV is a player and has a starting position. According to a predefined pattern in a diamond shape, the UAVs take turns flooding the neighbor cells. The UAVs cannot fly over building cells or cells previously occupied by other UAVs. The partitioning method guarantees an approximate amount of work for each assigned UAV by balancing the tasks. An improved version of the approach proposed by Trujillo et al. [74] was used for each sub-area’s coverage trajectories. The method can be classified initially as offline and then as online.

 

Table 3. Multi-UAV CPP strategies.

CPP ApproachType of UAVsAlgorithm ProcessingEvaluation MetricsReference
Sub-perimeter methodHomogeneousOnlineMinimize latency[63]
Back-and-ForthHomogeneousOnline/OfflineTotal path length

Time coverage		[23,66]
Back-and-ForthHeterogeneousOfflineNumber of turns[61]
SpiralHeterogeneousOfflineCoverage path, Number of turns[67,68]
Multi-Objective Path Planning with GAHomogeneousOffline/OnlineMission Completion Time[73]
GA with flood fill algorithmHomogeneousOffline/OnlinePath length[74,75]

3.21. Energy-Saving CPP Algorithms

In the literature, there are a lot of CPP strategies for energy saving. One method for energy saving proposed by Lawrance and Sukkarieh [25] is the energy exploitation of the wind using a small gliding UAV. The authors present an algorithm that generates energy gain paths according to the UAV’s constraints, the field’s wind conditions, and static and dynamic soaring. One of the limitations of this method is the requirement for prior knowledge of the field’s wind conditions. In future research, an online stochastic wind estimation and planning method using current wind conditions of the field should be developed.
Another method for minimizing the power consumption of a UAV is reducing the number of turns of the CPP. Torres et al. [76] present an algorithm that reduces the number of turns and the total flying path to minimize battery consumption.
The effect of wind direction and intensity on the time of mission completion was presented by Coombes et al. [77]. The authors used a fixed-wing UAV and the boustrophedon method to cover the area of interest. Their simulated experiments used a constant direction of the wind and six different speeds, and for the coverage path used different directions of the fixed-wing UAV motion from 0 to 360 degrees in increments of 10 degrees. The results showed that the direction of the coverage path should be 90 degrees to the wind direction to minimize the coverage time. Furthermore, the direction of the turns is directly affected by the vertical component of the wind. In a later work, Coombes et al. [78] presented the flight time in wind (FTIW) function, which computes the total flight time for a total coverage of the area of interest. The flight time needed for the total coverage of the area is less than the previous methods. Their approach was validated after simulations and real flights.
An energy-efficient back and forth CPP algorithm proposed by Di Franco and Buttazzo [18] computes the best motion trajectory and the maximum altitude according to the ground sample distance (image resolution) to minimize the number of turns. Another approach for energy efficiency is to find an optimal constant speed according to the coverage path. An energy-aware spiral CPP algorithm uses wider angle turns to minimize the acceleration and deceleration to maintain an optimal constant speed Cabreira et al. [79]. After simulated and real flights, the most energy-efficient CPP method between energy-efficient back and forth CPP [18] and the energy-aware spiral CPP approach proposed by Cabreira et al. [79] for a convex area was the energy-aware spiral CPP method which adopted the energy model proposed by Di Franco and Buttazo [80].
Another energy-aware CPP algorithm for UAVs was proposed by Li et al. [81], where the algorithm has three stages. In the first stage, the algorithm builds a 3D terrain model. In the second stage, constant power consumption is computed by total take-off weight, flight speed, and air friction. In the third stage, a genetic algorithm generates an energy-optimal coverage path, which represents the amount of energy consumption in every part of the path.
Another problem concerning UAV energy consumption is the deceleration and acceleration at every turn of a conventional trajectory such as boustrophedon. Artemenko et al. [82] present an algorithm that modifies conventional trajectories using Bézier curves, smoothing the turns on a given path to minimize deceleration and acceleration before and after the turning point. The authors concluded that their algorithm could reduce energy spending compared to conventional algorithms. Restrictions, such as the UAV motion and camera’s location, can be overcome using integer linear programming. Ahmadzadeh et al. [83] present a cooperative coverage technique with critical time for rectangular areas utilizing several fixed-wing heterogeneous UAVs, some carrying a frontal camera, flying circular paths and some of them carrying a camera on the left side, flying straight lines with left turn paths. Their proposed method uses four fixed-wing UAVs covering 100% of the area of interest instead of the simple methods covering 80%. The proposal was validated in simulation tests and real flights.
Araujo et al. [84] propose an algorithm where the workspace is divided into sub-areas assigned to each UAV according to its relative capability. According to the kinematics constraints of the UAVs, the algorithm generates an optimal number of stripes to minimize the number of stripes and eventually the number of turns, which means less energy consumption.
Majeed and Lee [85] present a CPP method for UAV low-altitude navigation in three-dimensional urban areas with fixed convex obstacles based on footprint sweeps fitting and a sparse waypoint graph. The primary goals of the proposed approach are to reduce computational time, the number of turns, and path overlapping while minimizing the total coverage path of the area of interest. The suggested method outperforms the similarly related CPP approaches according to simulation findings.
In a later work, Majeed and Hwang [86] present a CPP algorithm for UAV navigation to cover areas of interest (AOIs) surrounded by obstacles in three-dimensional urban areas with fixed obstacles. The proposed method is applicable in a wide range of practical applications that involve computing a low-cost coverage for spatially distributed AOIs in an urban environment. However, the proposed algorithm has not incorporated and tested for constraints and limitations, such as image resolution and UAV battery.
Cheng et al. [87] present a bio-inspired method for cooperative coverage. This method represents the trajectory of each UAV as the B-spline curve containing control points. This optimization problem aims to maximize the desirability of a path by combining four variables: path distance, minimum turning angle, maximum pitch rate, and superposition of the actual trajectory over different UAV trajectories. According to the authors, the beginning and last control points are at the area’s borders because the UAV always travels from left to right. The ant colony optimization (ACO) algorithm was adapted for coverage with multiple UAVs by Kuiper and Nadjm-Tehrani [88]. The y-axis in the intermediate control points is optimized using the ACO algorithm to maximize the coverage. Several ants are launched during the algorithm repetitions, passing through the starting, intermediate, and endpoints.
Table 4 summarizes the energy-saving CPP methods reviewed in this paper according to the method used for energy saving. The table presents the CPP method, the energy-saving factor, the type of UAV, and the corresponding reference.

Table 4. CPP energy-aware methods.

CPP MethodEnergy-Saving ApproachType of UAVReference
Energy gain pathEnergy exploitation of the windFixed-wing[25]
Back and ForthReducing the number of turns and the total flying pathRotorcraft[76]
BoustrophedonThe direction of the UAV path and the turns according to the wind directionFixed-wing[77]
Back and ForthAltitude maximization according to the Ground Sample Distance to reduce the number of turnsRotorcraft[18]
SpiralWider angle turns to minimize the acceleration and decelerationRotorcraft[79]
Three stages energy optimal pathAn energy-aware algorithm computes the take-off weight, flight speed, and air friction to generate an energy-optimal pathRotorcraft[81]
Smoothing turnsSmoothing the turns on a given path to minimize deceleration and acceleration before and after the turning pointRotorcraft/Fixed-wing[82]
Circular and straight lines with left turns pathsCooperative coverage algorithm with critical timeMultiple Fixed-wing[83]
Back and ForthMinimizing the number of stripes and eventually the number of turnsMultiple Fixed-wing[84]
Back and ForthReduce computational time, the number of turns, and path overlapping while minimizing the total coverage pathRotorcraft[85]
Back and ForthReducing the computational time and path length for the inter-regional path, the number of turning maneuvers, and path overlappingRotorcraft[86]
ACO with Gaussian distribution functionsPath length, rotation angle, and area overlapping rateRotorcraft/Fixed-wing[87]

4. Discussion

TMultiple robots have CPP probleman advantage over single robotic systems [24]. The use of multing UAVs iple robots accelerates coverage of an areas of interest with different shapes and environmental co. The problem of covering an area with multiple robots lies in the calculation of optimal routes in order to minimize the coverage time [30]. Usindg multitions has been studiple robots in a CPP work reduces the completion time due to workload division [20]. This section d by several authors. Standard-shaped areasiscusses multi-robot coverage methods based on single robot approaches, multi-robot strategies, and multiple UAVs to cover an area of interest, such as polygons and rectangles,. Some drawbacks of multiple UAV strategies are spatial orientation and communication difficulties. Table 2 at the endo not require of this section summarizes the multi-robot CPP strategies and presents the CPP approach, the decomposition and can be covmethod, the algorithm processing, and the corresponding reference.

12. Multi-Robot Boustrophedon Decomposition

Rekleitis et al. [16] presented by boustrophedon and spiral patterns. Generally, no a set of online algorithms for solving the CPP using a group of mobile robots in an unknown environment. The algorithms employ the same planar cellular decomposition methods, such as back-and-forth, require low computational cost to find the path trajectory. The main issueas the Boustrophedon single robot coverage algorithm, with additions to manage how robots cover a single cell and distribute among cells. Their solution takes into account the team members’ communication limitations. The robots serve two roles to accomplish coverage where some members, known as explorers, cover the boundaries of these patterns is not cons actual target cell, while others, known as coverers, conduct basic back-and-forth motions to cover the cell.

13. Multi-Robot Spanning Tree Coverage

Theidr experingmental data reveal that the UAVs are directly aerodynamicallyir technique outperforms multi-robot spanning tree coverage (MSTC) by a significant margin. Nevertheless, the coverage time of an area with the multi-robot forest coverage (MFC) algorithm is shorter than the MSTC algorithm [30]. Moreover, affn onlinected by t, robust version of MSTC was provided by Hazon et al. [47]. They environmentashow that the approach is robust analytically, providing as much coverage as a single robot can.

14. Multi-Robot Neural Network-Based Coverage

A neural network approaconditions, which meansh for multi-robot coverage where each robot sees all the others as obstacles and the actual trajectory ofvoidance ability of stalemate situations was proposed by Luo and Yang [46][48][49]. tThe flight in most cases is not close to that planned.
Imulti-robot neural-network based coverage is inspired by single robot neural-network coverage. During the coverage of the irregular-shaped area of interest, more complexthe robots see each other as moving obstacles.

15. Multi-Robot Graph-Based and Boundary Coverage

Easton and Burdick [50] presented a two-dimensional boundaregular areas of interest, a cellular decomposition method may be applied to split the area of interest into subregionsy coverage method for multiple robots. A team of robots must inspect all points on the boundary of the two-dimensional target environment, and each robot’s inspection routes are planned to use a heuristic search. The planned paths cover the entire boundary. Moreover, the algorithm has been validated by simulations. The multi-robot boundary coverage is inspired by the need to inspect the blade surfaces inside a turbine.
Table 2. Multi-robot CPP strategies.
CPP ApproachDecomposition MethodAlgorithm ProcessingReference
BoustrophedonExact cellularOnline[16]
Spanning Tree CoverageApproximate cellularOnline[47]
Neural network-basedApproximate cellularOnline[46][48][49]
Graph-based and BoundaryApproximate cellularOffline[50]

16. Multi-UAV CPP Methods

The snubregions mber of applications where UAVs can be covered by differentused is increasing as remote-sensing technology is developed. In the literature, there are a lot of multi-UAV CPP methods to obtain the optimum path to minimize the totalusing different coverage algorithms with heterogeneous or homogeneous UAVs that were used in a variety of applications, such as agriculture [51], surveillance [52], mapping [53], atnd search and the torescue missions [54]. Table 3 atal coverage flight time. Mthe end of this section summarizes the multi-UAV cooperative strategies are also being studied using CPP strategies and presents the CPP approach, the type of UAVs, the algorithm processing, the evaluation metrics, and the corresponding reference.

17. Multi-UAV Coverage

In the dagricultural secomposititor, Barrientos et al. [13] proponsed a method according to the capabilities of thefor area coverage using a fleet of mini aerial robots. Their method divides the area of interest in k non-overlapping subtasks and assigns them in k UAVs.
Wh A decentralized the vehicle used for themethod for surveillance missions using homogeneous UAVs was proposed CPP alby Acevedo et al. [55]. This method’s primary goral is to minimithms is a UAV, tze latency, which means a short sharing time of information between the UAVs. In a later work, Acevedo et al. [56] developed a method for survere is the limitation of thillance in urban environments with heterogeneous UAVs that fly at low altitudes and avoid obstacles. Finally, in their most recent work, Acevedo et al. [57] developed a motion constraints, such as the feasibleethod based on grid-shape area partition, which can readjust the area shape and UAVs’ capacity.
A terajectory of fixed-wing UAVs. However,rain coverage method using a fleet of heterogeneous UAVs was presented by Maza and Ollero [53]. tThe CPP methods plan their method divides the irregular-shaped area of interest per each UAV capability, such as total flight time. Each partition is assigned to a UAV that plans a zig-zag coverage pathing pattern according to a performance metric. These approaches do not the area’s characteristics to minimize the number of turns. The method was validated in simulation.
A considver the UAVs’ environmental factors and aerodynamic and flight lage algorithm for fixed-wing UAVs with the ability for obstacle and previously scanned regions avoidance was presented by Xu et al. [23][58]. Their mitations.
Aethod uses fbourther studystrophedon cellular decomposition is[25], anecessary for the area of CPP exact cellular decomposition, and presents better accuracy than trapezoidal decomposition. The methods using UAVs. T can be classified as online in the phase of region scanning and offline in the coverage aphase.

18. Back-and-Forth

Maza and Ollgero [53] present a cooperithms should consider the constraints of the aerial vehicles, such as the actual path trajectory rather thative technique using heterogeneous UAVs in a convex polygonal area. A ground control station divides the area into sub-regions and assigns them to every UAV by the capability and starting position. Every UAV calculates back-and-forth patterns according to the camera footprint to reduce the number of turns.

19. Spiral

Balampanis thaet al. [59][60] present a planned. Moreover, the environmspiral CPP algorithm using multiple heterogeneous UAVs. The area of interest is divided according to UAVs sensing capabilities using a constrained Delaunay triangulation (CDT) [61]. The CDT generatal factors ines triangle cells that match almost exactly the shape of the area of interest that affect the path, the time, and. To make the triangles more uniform, they applied Lloyd optimization [62]. tThe actual flight path should also ben, a spiral algorithm generates the coverage pattern for each sub-area. This method can generate smoother trajectories considered. According to all these mutable factors, an offline CPP method will not achieve optiming avoiding no-fly zones and the shape of the coverage area. However, it generates more extensive coverage paths and a higher number of turns than classical grid decomposition and motion methods [63][64].

20. Multi-Objective Path Planning (MOPP) with Genetic Algorithm (GA)

Hayat et al. [65] propose multi-objective path planning, but an online CPP method considering all these factors (MOPP) with a genetic algorithm (GA) for search and rescue missions using multiple UAVs. The mission is divided into two phases: search and re-planningsponse. The search phase monitors an event to guarantee the trajectory will achieve the optimal coverage path withinotal coverage in a given area, and the response phase spreads detection updates on the network. The MOPP algorithm performs the planning task during the search, while the GA minimum time.
Iizes the mission recent years, many new CPP algorithms have been ompletion time. As a result, the method can be classified as offline in the search phase and online in the response phase.

21. Genetic Algorithm (GA) with Flood Fill Algorithm

Based on thevel Trujillo et al. [66] approach, Darrah et al. [67] present a CPP method for energy-efficiency and awarenesmissions over more extensive areas using multi-UAVs. The approach using a glider UAV for soaring limits early knowledge of the field’s wind conditions. Otherwise, the method is less effectivemethod produces equitable sub-areas of the area of interest to cover by multi-UAVs or several flights performed by a single UAV. The flood fill algorithm integrated with game theory was applied to partition the area of interest. Each UAV is a player and has a starting position. According to a predefined pattern in a situation where the knowledge of wind conditions is limited [25].diamond shape, the UAVs take turns flooding the neighbor cells. The UAVs cannot fly over building cells or cells previously occupied by other UAVs. The partitioning method guarantees Ian approaches where engine-drivenximate amount of work for each assigned UAV by balancing the tasks. An improved version of the approach proposed by Trujillo et al. UAVs[66] ware used, there are soms used for each sub-area’s coverage trajectories. The methods or combin can be classified initially as offline and then as online.

Table 3. Multi-UAV CPP strategies.

CPP ApproachType of UAVsAlgorithm ProcessingEvaluation MetricsReference
Sub-perimeter methodHomogeneousOnlineMinimize latency[55]
Back-and-ForthHomogeneousOnline/OfflineTotal path length

Time coverage		[23][58]
Back-and-ForthHeterogeneousOfflineNumber of turns[53]
SpiralHeterogeneousOfflineCoverage path, Number of turns[59][60]
Multi-Objective Path Planning with GAHomogeneousOffline/OnlineMission Completion Time[65]
GA with flood fill algorithmHomogeneousOffline/OnlinePath length[66][67]

22. Energy-Saving CPP Algorithms

In the literature, there are a lot of CPP strategiones for energy saving. AOne method for powerenergy saving in non-complex areasproposed by Lawrance and Sukkarieh [68] is the enereducing the number of turns in tgy exploitation of the wind using a small gliding UAV. The authors present an algorithm that generates energy gain paths according to the UAV’s trajectory to minimize the total path and the accelconstraints, the field’s wind conditions, and static and dynamic soaring. One of the limitations of this method is the requirement for prior knowledge of the field’s wind conditions. In future research, an online stochastic wind estimation and planning method using current wind conditions of the field should be developed.
Anothera metion’shod for minimizing the power consumption after ev of a UAV is reducing the number of turns of the CPP. Torres et al. [69] present an algorithm that reduces the numbery of turn, and eventually the tots and the total flying path to minimize battery consumption.
The effect of wind direction and intensity on the time of mission compl covetion was presented by Coombes et al. [70]. The authorage time ofs used a fixed-wing UAV and the boustrophedon method to cover the area of interest [20,76]. InTheir approaches for energy saving, considering the direction and intensity of the wind was validated as the UAV’ssimulated experiments used a constant direction of the wind and six different speeds, and for the coverage path used different directions of the fixed-wing UAV motion from 0 to 360 degrees in increments of 10 degrees. The results showed that the direction of the coverage path should be vertical in the wind90 degrees to the wind direction to minimize the coverage time. Furthermore, the direction, and of the turning maneuvers against s is directly affected by the vertical component of the wind . In a later work, Coombes et al. [71] presented the flirection [77ght time in wind (FTIW) function,78]. Twhis approach can be combined withch computes the total flight time for a total coverage of the area of interest. The flight time needed for the total coverage of the area is less than the previous method for greater es. Their approach was validated after simulations and real flights.
An energy saving.
Tw-efficient back and forth more approaCPP algorithm proposed by Di Franco and Buttazzo [18] computes thes that can be used in combination with the previous methods for further best motion trajectory and the maximum altitude according to the ground sample distance (image resolution) to minimize the number of turns. Another approach for energy saving include minimizing the UAV’s turnsefficiency is to find an optimal constant speed according to the GSD [18]coverage path. An energy-aware spiral CPP algorithm uses wider angle turns to maintain a inimize the acceleration and deceleration to maintain an optimal constant speed [67]Cabreira et al. [72]. oAfter an algorithm forsimulated and real flights, the most energy-efficient CPP method between energy-efficient back and forth CPP [18] and conventional trajectthe energy-aware spiral CPP approach proposed by Cabreira et al. [72] fory that modifiea convex area was the turns for smoother motion [70] energy-aware spiral CPP method which adopted the energy model proposed by Di Franco and Buttazo mi[73].
Animize othe deceleration and accelr energy-aware CPP algorithm for UAVs was proposed by Li et al. [74], where the ation before and after the turning point. Another energy-aware algorithmlgorithm has three stages. In the first stage, the algorithm builds a 3D terrain model. In the second stage, constant power consumption is computes thed by total take-off weight, flight speed, and air friction ton. In the third stage, a genetic algorithm generates an energy-optimal path [81].
Icoverage path, which represents the amount of energy convex areas, sumption in every part of the path.
Anothere are approaches using multiple UAVs to divide into sub-areasproblem concerning UAV energy consumption is the deceleration and assign each sub-area according to the UAV’s capability,cceleration at every turn of a conventional trajectory such as motion, sensoboustrophedon. Artemenko et al. [75] pres onboard, and total endurance flight time [83ent an algorithm that modifies conventional trajectories using Bézier curves,84].
T smoothing the pturoposed energy-efficient UAV CPP methods aim ns on a given path to minimize the total flight timdeceleration and acceleration before and the coverage path length to save energy. However, the performance metrics are based on the path trajectory without considering other constraintafter the turning point. The authors concluded that their algorithm could reduce energy spending compared to conventional algorithms. Restrictions, such as UAV aerodynamics and environmental conditions. For examthe UAV motion and camera’s location, can be overcome using integer linear programming. Ahmadzadeh et al. [76] plrese, in a convex area, a CPP methodnt a cooperative coverage technique with a performance metric for minimum path trajectory may produce very sharp turns. Meanwhile, it is infeasible for a critical time for rectangular areas utilizing several fixed-wing heterogeneous UAVs, some carrying a frontal camera, flying circular paths and some of them carrying a camera on the left side, flying straight lines with left turn paths. Their proposed method uses four fixed-wing UAV to obtain the planned ts covering 100% of the area of interest instead of the simple methods covering 80%. The proposal was validated in simulation tests and real flights.
Araujeo et al. [77] propose an algorithm where the workspace is divided intory due sub-areas assigned to each UAV according to its aerodynamrelative capability. According to the kinematics constraints. Another variable affecting the UAV’s actual trajecto of the UAVs, the algorithm generates an optimal number of stripes to minimize the number of stripes and eventually the number of turns, which means less energy consumption.
Majeed and Lee [78] pryesent a is the wind’s direction and intensityCPP method for UAV low-altitude navigation in three-dimensional urban areas with fixed convex obstacles based on footprint sweeps fitting and a sparse waypoint graph. The UAV will consume more energy than a more extensivprimary goals of the proposed approach are to reduce computational time, the number of turns, and path overlapping while minimizing the total coverage path length with smoother turns consideringof the area of interest. The suggested method outperforms the similarly related CPP approaches according to simulation findings.
In a llater work, Majeed and Hwang [79] thprese limitations.
Ant a CPP algorithm for UAV navigation to cover areas ofurther study is necessary to combine all of the above constraints to develop new energy-efficient UAV CPP methods that consider variable interest (AOIs) surrounded by obstacles in three-dimensional urban areas with fixed obstacles. The proposed method is applicable in a wide range of practical applications that involve computing a low-cost coverage for spatially distributed AOIs in an urban environment. However, the proposed algorithm has not incorporated and tested for constraints and limitations, such as the vehicle kinematics and enviroimage resolution and UAV battery.
Chenmg entalt al. co[80] presenditions offline and online. A research direction to develop UAV CPP method a bio-inspired method for cooperative coverage. This method represents the trajectory of each UAV as the B-spline curve containing control points. This optimization problem aims to maximize energy-saving should combine machine learning or deep learthe desirability of a path by combining four variables: path distance, minimum turning angle, maximum pitch rate, and superposition of the actual trajectory over different UAV trajectories. According to the authors, the beginning and IoT onboard sensors in order to develop a CPP approach that will plan last control points are at the area’s borders because the UAV always travels from left to right. The ant colony optimization (ACO) algorithm was adapted for coverage with multiple UAVs by Kuiper and Nadjm-Tehrani offl[81]. The y-axis in the and adapt onlinintermediate control points is optimized using the ACO algorithm to maximize the coverage path trajectory according to the main performance met. Several ants are launched during the algorithm repetitions, passing through the starting, intermediate, and endpoints.
Table 4 summariczes, such as UAV kinematics constraints, and the information retrieved from onboard sensors such as wind conditions the energy-saving CPP methods reviewed in this paper according to the method used for energy saving. The table presents the CPP method, the energy-saving factor, the type of UAV, and the corresponding reference.

 Table 4. CPP energy-aware methods.

 

CPP MethodEnergy-Saving ApproachType of UAVReference
Energy gain pathEnergy exploitation of the windFixed-wing[68]
Back and ForthReducing the number of turns and the total flying pathRotorcraft[69]
BoustrophedonThe direction of the UAV path and the turns according to the wind directionFixed-wing[70]
Back and ForthAltitude maximization according to the Ground Sample Distance to reduce the number of turnsRotorcraft[18]
SpiralWider angle turns to minimize the acceleration and decelerationRotorcraft[72]
Three stages energy optimal pathAn energy-aware algorithm computes the take-off weight, flight speed, and air friction to generate an energy-optimal pathRotorcraft[74]
Smoothing turnsSmoothing the turns on a given path to minimize deceleration and acceleration before and after the turning pointRotorcraft/Fixed-wing[75]
Circular and straight lines with left turns pathsCooperative coverage algorithm with critical timeMultiple Fixed-wing[76]
Back and ForthMinimizing the number of stripes and eventually the number of turnsMultiple Fixed-wing[77]
Back and ForthReduce computational time, the number of turns, and path overlapping while minimizing the total coverage pathRotorcraft[78]
Back and ForthReducing the computational time and path length for the inter-regional path, the number of turning maneuvers, and path overlappingRotorcraft[79]
ACO with Gaussian distribution functionsPath length, rotation angle, and area overlapping rateRotorcraft/Fixed-wing[80]

 

References

  1. Lagkas, T.; Argyriou, V.; Bibi, S.; Sarigiannidis, P. UAV IoT Framework Views and Challenges: Towards Protecting Drones as “Things”. Sensors 2018, 18, 4015.
  2. Azpúrua, H.; Freitas, G.M.; Macharet, D.G.; Campos, M.F.M. Multi-Robot Coverage Path Planning Using Hexagonal Segmentation for Geophysical Surveys. Robotica 2018, 36, 1144–1166.
  3. Maes, W.H.; Steppe, K. Perspectives for Remote Sensing with Unmanned Aerial Vehicles in Precision Agriculture. Trends Plant Sci. 2019, 24, 152–164.
  4. Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A Compilation of UAV Applications for Precision Agriculture. Comput. Netw. 2020, 172, 107148.
  5. Silvagni, M.; Tonoli, A.; Zenerino, E.; Chiaberge, M. Multipurpose UAV for Search and Rescue Operations in Mountain Avalanche Events. Geomat. Nat. Hazards Risk 2017, 8, 18–33.
  6. Yuan, C.; Liu, Z.; Zhang, Y. Aerial Images-Based Forest Fire Detection for Firefighting Using Optical Remote Sensing Techniques and Unmanned Aerial Vehicles. J. Intell. Robot. Syst. 2017, 88, 635–654.
  7. Straub, J. Unmanned Aerial Systems: Consideration of the Use of Force for Law Enforcement Applications. Technol. Soc. 2014, 39, 100–109.
  8. Deng, C.; Wang, S.; Huang, Z.; Tan, Z.; Liu, J. Unmanned Aerial Vehicles for Power Line Inspection: A Cooperative Way in Platforms and Communications. J. Commun. 2014, 9, 687–692.
  9. Cho, J.; Lim, G.; Biobaku, T.; Kim, S.; Parsaei, H. Safety and Security Management with Unmanned Aerial Vehicle (UAV) in Oil and Gas Industry. Procedia Manuf. 2015, 3, 1343–1349.
  10. Erdelj, M.; Natalizio, E. UAV-assisted disaster management: Applications and open issues. In Proceedings of the 2016 International Conference on Computing, Networking and Communications (ICNC), Kauai, HI, USA, 15–18 February 2016; pp. 1–5.
  11. Pliatsios, D.; Goudos, S.K.; Lagkas, T.; Argyriou, V.; Boulogeorgos, A.A.A.; Sarigiannidis, P. Drone-Base-Station for Next-Generation Internet-of-Things: A Comparison of Swarm Intelligence Approaches. IEEE Open J. Antennas Propag. 2021, 3, 32–47.
  12. Ballesteros, R.; Ortega, J.F.; Hernández, D.; Moreno, M.A. Applications of Georeferenced High-Resolution Images Obtained with Unmanned Aerial Vehicles. Part I: Description of Image Acquisition and Processing. Precis. Agric. 2014, 15, 579–592.
  13. Barrientos, A.; Colorado, J.; del Cerro, J.; Martinez, A.; Rossi, C.; Sanz, D.; Valente, J. Aerial Remote Sensing in Agriculture: A Practical Approach to Area Coverage and Path Planning for Fleets of Mini Aerial Robots. J. Field Robot. 2011, 28, 667–689.
  14. Maza, I.; Capitán, J.; Merino, L.; Ollero, A. Multi-UAV cooperation. In Encyclopedia of Aerospace Engineering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2015; pp. 1–10.
  15. Spyridis, Y.; Lagkas, T.; Sarigiannidis, P.; Zhang, J. Modelling and Simulation of a New Cooperative Algorithm for UAV Swarm Coordination in Mobile RF Target Tracking. Simul. Model. Pract. Theory 2021, 107, 102232.
  16. Rekleitis, I.; New, A.P.; Rankin, E.S.; Choset, H. Efficient Boustrophedon Multi-Robot Coverage: An Algorithmic Approach. Ann. Math. Artif. Intell. 2008, 52, 109–142.
  17. Nolan, P.; Paley, D.A.; Kroeger, K. Multi-UAS path planning for non-uniform data collection in precision agriculture. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; pp. 1–12.
  18. Di Franco, C.; Buttazzo, G. Coverage Path Planning for UAVs Photogrammetry with Energy and Resolution Constraints. J. Intell. Robot. Syst. 2016, 83, 445–462.
  19. Choset, H. Coverage for Robotics—A Survey of Recent Results. Ann. Math. Artif. Intell. 2001, 31, 113–126.
  20. Galceran, E.; Carreras, M. A Survey on Coverage Path Planning for Robotics. Robot. Auton. Syst. 2013, 61, 1258–1276.
  21. Valente, J.; Del Cerro, J.; Barrientos, A.; Sanz, D. Aerial Coverage Optimization in Precision Agriculture Management: A Musical Harmony Inspired Approach. Comput. Electron. Agric. 2013, 99, 153–159.
  22. Paull, L.; Thibault, C.; Nagaty, A.; Seto, M.; Li, H. Sensor-Driven Area Coverage for an Autonomous Fixed-Wing Unmanned Aerial Vehicle. IEEE Trans. Cybern. 2014, 44, 1605–1618.
  23. Xu, A.; Viriyasuthee, C.; Rekleitis, I. Optimal complete terrain coverage using an unmanned aerial vehicle. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2513–2519.
  24. Fazli, P.; Davoodi, A.; Mackworth, A.K. Multi-Robot Repeated Area Coverage. Auton. Robots 2013, 34, 251–276.
  25. Choset, H.; Pignon, P. Path Planning: The Boustrophedon Cellular Decomposition. In Proceedings of the International Conference on Field and Service Robotics, Canberra, Australia, 12 October 1997; pp. 1311–1320.
  26. Choset, H.; Pignon, P. Coverage path planning: The boustrophedon cellular decompositio. In Field and Service Robotics; Springer: London, UK, 1998; pp. 203–209.
  27. Choset, H.; Acar, E.; Rizzi, A.A.; Luntz, J. Exact cellular decompositions in terms of critical points of Morse functions. In Proceedings of the 2000 ICRA. Millennium Conference, IEEE International Conference on Robotics and Automation, Symposia Proceedings (Cat. No.00CH37065), San Francisco, CA, USA, 24–28 April 2000; Volume 3, pp. 2270–2277.
  28. Andersen, H.L. Path Planning for Search and Rescue Mission Using Multicopters. 2014. 135. Available online: https://ntnuopen.ntnu.no/ntnu-xmlui/handle/11250/261317 (accessed on 12 December 2021).
  29. LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006.
  30. Zheng, X.; Jain, S.; Koenig, S.; Kempe, D. Multi-robot forest coverage. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 3852–3857.
  31. Choset, H.; Lynch, K.M.; Hutchinson, S.; Kantor, G.A.; Burgard, W. Principles of Robot Motion: Theory, Algorithms, and Implementations; MIT Press: Cambridge, MA, USA, 2005.
  32. Latombe, J.-C. Robot Motion Planning; Stanford University, Kluwer Academic Publishers: New York, NY, USA, 1991.
  33. Oksanen, T.; Visala, A. Coverage Path Planning Algorithms for Agricultural Field Machines. J. Field Robot. 2009, 26, 651–668.
  34. Acar, E.U.; Choset, H.; Rizzi, A.A.; Atkar, P.N.; Hull, D. Morse Decompositions for Coverage Tasks. Int. J. Robot. Res. 2002, 21, 331–344.
  35. SStein, E.; Milnor, J.W.; Spivak, M.; Wells, R.; Wells, R.; Mather, J.N. Morse Theory; Princeton University Press: Princeton, NJ, USA, 1963; ISBN 978-0-691-08008-6.
  36. Acar, E.U.; Choset, H.; Atkar, P.N. Complete sensor-based coverage with extended-range detectors: A hierarchical decomposition in terms of critical points and Voronoi diagrams. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems, Expanding the Societal Role of Robotics in the the Next Millennium (Cat. No.01CH37180), Maui, HI, USA, 29 October–3 November 2001; Volume 3, pp. 1305–1311.
  37. Acar, E.U.; Choset, H. Sensor-Based Coverage of Unknown Environments: Incremental Construction of Morse Decompositions. Int. J. Robot. Res. 2002, 21, 345–366.
  38. Wong, S. Qualitative Topological Coverage of Unknown Environments by Mobile Robots; The University of Auckland: Auckland, New Zealand, 2006.
  39. Wong, S.C.; MacDonald, B.A. Complete coverage by mobile robots using slice decomposition based on natural landmarks. In PRICAI 2004: Trends in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2004; pp. 683–692.
  40. Butler, Z.J.; Rizzi, A.A.; Hollis, R.L. Contact sensor-based coverage of rectilinear environments. In Proceedings of the 1999 IEEE International Symposium on Intelligent Control Intelligent Systems and Semiotics (Cat. No.99CH37014), Cambridge, MA, USA, 17 September 1999; pp. 266–271.
  41. Moravec, H.; Elfes, A. High resolution maps from wide angle sonar. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation Proceedings, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 116–121.
  42. Zelinsky, A.; Jarvis, R.A.; Byrne, J.C.; Yuta, S. Planning Paths of Complete Coverage of an Unstructured Environment by a Mobile Robot. In Proceedings of the International Conference on Advanced Robotics, Tsukuba, Japan, 11 September 1993; Volume 13, pp. 533–538.
  43. Shivashankar, V.; Jain, R.; Kuter, U.; Nau, D. Real-Time Planning for Covering an Initially-Unknown Spatial Environment. In Proceedings of the Twenty-Fourth International FLAIRS Conference, Palm Beach, FL, USA, 20 March 2011.
  44. Gabriely, Y.; Rimon, E. Spiral-STC: An on-Line Coverage Algorithm of Grid Environments by a Mobile Robot. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 1, pp. 954–960.
  45. Luo, C.; Yang, S.X.; Stacey, D.A.; Jofriet, J.C. A Solution to Vicinity Problem of Obstacles in Complete Coverage Path Planning. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 1, pp. 612–617.
  46. Yang, S.X.; Luo, C. A Neural Network Approach to Complete Coverage Path Planning. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2004, 34, 718–724.
  47. Hazon, N.; Mieli, F.; Kaminka, G.A. Towards Robust On-Line Multi-Robot Coverage. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, ICRA 2006, Orlando, FL, USA, 15–19 May 2006; pp. 1710–1715.
  48. Luo, C.; Yang, S.X. A real-time cooperative sweeping strategy for multiple cleaning robots. In Proceedings of the of the IEEE Internatinal Symposium on Intelligent Control, Vancouver, BC, Canada, 30 October 2002; pp. 660–665.
  49. Luo, C.; Yang, S.X.; Stacey, D.A. Real-time path planning with deadlock avoidance of multiple cleaning robots. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), Taipei, Taiwan, 14–19 September 2003; Volume 3, pp. 4080–4085.
  50. Easton, K.; Burdick, J. Inspection’. In Proceedings of the Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 727–734.
  51. Ju, C.; Son, H. Multiple UAV Systems for Agricultural Applications: Control, Implementation, and Evaluation. Electronics 2018, 7, 162.
  52. Vincent, P.; Rubin, I. A framework and analysis for cooperative search using UAV swarms. In Proceedings of the 2004 ACM symposium on Applied Computing, New York, NY, USA, 14 March 2004; pp. 79–86.
  53. Maza, I.; Ollero, A. Multiple UAV cooperative searching operation using polygon area decomposition and efficient coverage algorithms. In Distributed Autonomous Robotic Systems 6; Springer: Tokyo, Japan, 2007; pp. 221–230.
  54. Alotaibi, E.T.; Alqefari, S.S.; Koubaa, A. LSAR: Multi-UAV Collaboration for Search and Rescue Missions. IEEE Access 2019, 7, 55817–55832.
  55. Acevedo, J.J.; Arrue, B.C.; Maza, I.; Ollero, A. Cooperative Large Area Surveillance with a Team of Aerial Mobile Robots for Long Endurance Missions. J. Intell. Robot. Syst. 2013, 70, 329–345.
  56. Acevedo, J.J.; Arrue, B.C.; Maza, I.; Ollero, A. Distributed Approach for Coverage and Patrolling Missions with a Team of Heterogeneous Aerial Robots under Communication Constraints. Int. J. Adv. Robot. Syst. 2013, 10, 28.
  57. Acevedo, J.J.; Arrue, B.C.; Diaz-Bañez, J.M.; Ventura, I.; Maza, I.; Ollero, A. One-to-One Coordination Algorithm for Decentralized Area Partition in Surveillance Missions with a Team of Aerial Robots. J. Intell. Robot. Syst. 2014, 74, 269–285.
  58. Xu, A.; Viriyasuthee, C.; Rekleitis, I. Efficient Complete Coverage of a Known Arbitrary Environment with Applications to Aerial Operations. Auton. Robots 2014, 36, 365–381.
  59. Balampanis, F.; Maza, I.; Ollero, A. Area Decomposition, Partition and Coverage with Multiple Remotely Piloted Aircraft Systems Operating in Coastal Regions. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 275–283.
  60. Balampanis, F.; Maza, I.; Ollero, A. Coastal Areas Division and Coverage with Multiple UAVs for Remote Sensing. Sensors 2017, 17, 808.
  61. Kallmann, M.; Bieri, H.; Thalmann, D. Fully Dynamic Constrained Delaunay Triangulations. In Geometric Modeling for Scientific Visualization; Springer: Berlin/Heidelberg, Germany, 2004; pp. 241–257.
  62. Shewchuk, J.R. Mesh generation for domains with small angles. In Proceedings of the Sixteenth Annual Symposium on Computational Geometry, New York, NY, USA, 1 May 2000; pp. 1–10.
  63. Balampanis, F.; Maza, I.; Ollero, A. Spiral-like coverage path planning for multiple heterogeneous UAS operating in coastal regions. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 617–624.
  64. Balampanis, F.; Maza, I.; Ollero, A. Area Partition for Coastal Regions with Multiple UAS. J. Intell. Robot. Syst. 2017, 88, 751–766.
  65. Hayat, S.; Yanmaz, E.; Brown, T.X.; Bettstetter, C. Multi-objective UAV path planning for search and rescue. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5569–5574.
  66. Trujillo, M.M.; Darrah, M.; Speransky, K.; DeRoos, B.; Wathen, M. Optimized flight path for 3D mapping of an area with structures using a multirotor. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016; pp. 905–910.
  67. Darrah, M.; Trujillo, M.M.; Speransky, K.; Wathen, M. Optimized 3D mapping of a large area with structures using multiple multirotors. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 716–722.
  68. Lawrance, N.; Sukkarieh, S. Wind Energy Based Path Planning for a Small Gliding Unmanned Aerial Vehicle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, American Institute of Aeronautics and Astronautics, Chicago, IL, USA, 10–13 August 2009.
  69. Torres, M.; Pelta, D.A.; Verdegay, J.L.; Torres, J.C. Coverage Path Planning with Unmanned Aerial Vehicles for 3D Terrain Reconstruction. Expert Syst. Appl. 2016, 55, 441–451.
  70. Coombes, M.; Chen, W.-H.; Liu, C. Boustrophedon Coverage Path Planning for UAV Aerial Surveys in Wind. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1563–1571.
  71. Coombes, M.; Fletcher, T.; Chen, W.-H.; Liu, C. Optimal Polygon Decomposition for UAV Survey Coverage Path Planning in Wind. Sensors 2018, 18, 2132.
  72. Cabreira, T.M.; Franco, C.D.; Ferreira, P.R.; Buttazzo, G.C. Energy-Aware Spiral Coverage Path Planning for UAV Photogrammetric Applications. IEEE Robot. Autom. Lett. 2018, 3, 3662–3668.
  73. Di Franco, C.; Buttazzo, G. Energy-Aware Coverage Path Planning of UAVs. In Proceedings of the 2015 IEEE International Conference on Autonomous Robot Systems and Competitions, Vila Real, Portugal, 8–10 April 2015; pp. 111–117.
  74. Li, D.; Wang, X.; Sun, T. Energy-Optimal Coverage Path Planning on Topographic Map for Environment Survey with Unmanned Aerial Vehicles. Electron. Lett. 2016, 52, 699–701.
  75. Artemenko, O.; Dominic, O.J.; Andryeyev, O.; Mitschele-Thiel, A. Energy-aware trajectory planning for the localization of mobile devices using an unmanned aerial vehicle. In Proceedings of the 2016 25th International Conference on Computer Communication and Networks (ICCCN), Waikoloa, HI, USA, 1–4 August 2016; pp. 1–9.
  76. Ahmadzadeh, A.; Keller, J.; Pappas, G.; Jadbabaie, A.; Kumar, V. An optimization-based approach to time-critical cooperative surveillance and coverage with UAVs. In Experimental Robotics: The 10th International Symposium on Experimental Robotics; Khatib, O., Kumar, V., Rus, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 491–500.
  77. Araujo, J.F.; Sujit, P.B.; Sousa, J.B. Multiple UAV area decomposition and coverage. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence for Security and Defense Applications (CISDA), Singapore, 16–19 April 2013; pp. 30–37.
  78. Majeed, A.; Lee, S. A New Coverage Flight Path Planning Algorithm Based on Footprint Sweep Fitting for Unmanned Aerial Vehicle Navigation in Urban Environments. Appl. Sci. 2019, 9, 1470.
  79. Majeed, A.; Hwang, S.O. A Multi-Objective Coverage Path Planning Algorithm for UAVs to Cover Spatially Distributed Regions in Urban Environments. Aerospace 2021, 8, 343.
  80. Cheng, C.-T.; Fallahi, K.; Leung, H.; Tse, C.K. Cooperative Path Planner for UAVs Using ACO Algorithm with Gaussian Distribution Functions. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 173–176.
  81. Kuiper, E.; Nadjm-Tehrani, S. Mobility Models for UAV Group Reconnaissance Applications. In Proceedings of the 2006 International Conference on Wireless and Mobile Communications (ICWMC’06), Bucharest, Romania, 29–31 July 2006; p. 33.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback