You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is a comparison between Version 3 by Bruce Ren and Version 2 by Bruce Ren.
Carbon materials, such as graphene nanoflakes, carbon nanotubes, and fullerene, can be widely used to store hydrogen, and doping these materials with lithium (Li) generally increases their H2-storage densities. Unfortunately, Li is expensive; therefore, alternative metals are required to realize a hydrogen-based society. Sodium (Na) is an inexpensive element with chemical properties that are similar to those of lithium.
- DFT
- biding energy
- electronic states
- coordination number
1. Introduction
Measures that counter climate change are of considerable international urgency [1][2][3][4][5]. Decarbonization is an effective method for reducing greenhouse gas emissions and achieving carbon neutrality [6][7][8][9][10]. In particular, the use of hydrogen energy is the key to decarbonized fuel [11][12].
The establishment of appropriate transportation methods is an important factor when socially implementing hydrogen energy [13][14]. Carbon materials can safely store hydrogen [15][16]; in particular, lithium (Li)-doped graphene and carbon nanotubes (CNTs) have been used as effective storage materials [17][18]. Unfortunately, lithium is expensive because it is generally shipped from various international locations to China for processing into various products; therefore, alternative metals are required to realize a hydrogen-based society. In this regard, sodium (Na) is an inexpensive metal with chemical properties similar to those of Li.
Interactions between sodium with carbon materials have been investigated both theoretically and experimentally. Moon et al. used density functional theory (DFT) calculations to investigate the adsorption of Na by graphene and graphene oxide, which are used as anode materials in sodium-ion batteries [19]. The adsorption energy for Na on graphene was found to be −0.507 eV at hollow sites, which is indicative of favorable adsorption, while Na atoms were found to separately adsorb at the epoxide and hydroxyl functional groups of graphene oxide; indeed, Na is more strongly adsorbed at the epoxide sites of graphene oxide (adsorption energy: −1.024 eV) than on pristine graphene.
Zhu and Lu used DFT calculations to investigate the adsorptions of Li, Na, and K on graphene surfaces [20]; all three metal atoms were found to preferentially adsorb at hexagonal graphene sites, with Na more-weakly bound than Li or K because the singly occupied molecular orbital (SOMO) of the Na atom lies exactly halfway in energy between the HOMO and the LUMO of the graphite layer.
Dimakis et al. investigated the multiple adsorption of Na onto a graphene surface using DFT calculations [21], which revealed that multiply adsorbed Na atoms are not stable on graphene at high coverages; however, the presence of defects on the graphene support was found to stabilize the adsorbed Na. Higher Na coverage results in metal nucleation that weakens adsorption. Consequently, alkali-metal-doped graphene nanoflakes have been extensively investigated.
H2 adsorption onto Na-decorated materials has also been investigated. Kassaoui et al. used DFT calculations to investigate the adsorption of H2 on Na-decorated tetragonal silicon carbide (t-SiC) [22] and found that Na-decoration enhances the hydrogen-storage properties of t-SiC.
Previously, the researchers investigated the mechanism of hydrogen storage in a graphene nanoflake (GR) doped by a lithium atom or lithium ion (i.e., the GR-M-(H2)n system, where M = Li or Li+, and n = 0–10) by DFT [23]. The binding energies of H2 to GR were calculated to be 3.83 kcal/mol (GR-Li) and 4.13 kcal/mol (GR-Li+), which suggests that the GR-Li system can be used to store H2. The researchers showed that electron transfer from Li to graphene plays an important role in the adsorption of H2. In addition, the researchers demonstrated that the graphene–lithium system can effectively store molecular H2. Analogously, the magnesium-based GR-Mg-H2 system has reportedly been used in a reversible hydrogen-storage device [24].
2. Hydrogen Storage Mechanism in Sodium-Based Graphene Nanoflakes
2.1. Structures of Na Doped-Graphene Nanoflakes
The optimized structures of GR-Na and GR-Na+ are shown in Figure 1, respectively. Both Na and Na+ are bound to hexagonal sites on the GR surface. The Na-surface distance, Na-GR binding energy, and NPA-determined atomic charge of Na are listed in Table 1 together with those of Na+, Li, and Li+. The distances between Na, Na+, and the GR surface were calculated to be 2.247 and 2.288 Å, respectively; Na is slightly closer to the surface than Na+. The binding energies of Na and Na+ were calculated to be 4.4 and 37.5 kcal/mol, respectively, which indicates that Na+ is bound about nine times more strongly than Na.
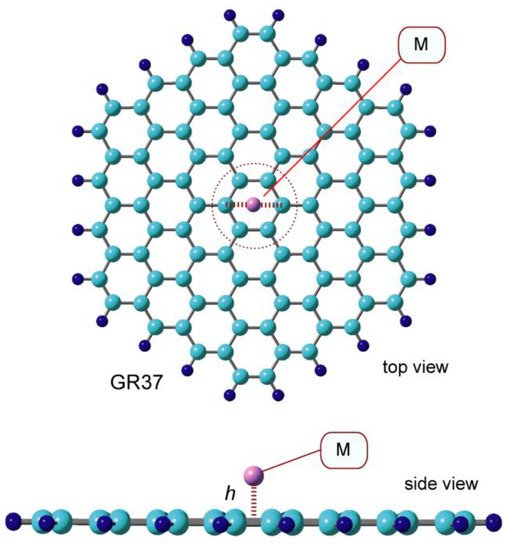

Figure 1. CAM-B3LYP/6-311G(d,p)—optimized structure of GR-Na (atom) with a GR composed of 37 benzene rings.
Table 1. M-GR and M+-GR binding energies (Ebind in kcal/mol, M = Li, Na), M-GR-surface distances (h in Å), and NPA-determined atomic charges for M on GR, calculated at the CAM-B3LYP/6-311G(d,p) level.
| Ebind | Height (h) | NPA | |
|---|---|---|---|
| GR-Na | 4.4 | 2.247 | +0.978 |
| GR-Na+ | 37.5 | 2.288 | +0.979 |
| GR-Li | 17.1 | 1.736 | +0.929 |
| GR-Li+ | 52.8 | 1.771 | +0.937 |
The NPA-determined atomic charges on Na and Na+ are +0.978 and +0.979, respectively; clearly, the net charge of Na is very similar to that of Na+, which suggests that significant Na-to-GR electron transfer occurs during binding (0.98e). These features are in good agreement with the GR-Li and GR-Li+ systems, as summarized in Table 1, where the NPA-determined atomic charges on Li and Li+ are +0.929 and +0.937, respectively.
2.2. Structures of Molecular Hydrogen Bound to GR-Na
The geometries of the GR-Na-(H2)n systems (n = 1–12) were fully optimized at the CAM-B3LYP/6-311G(d,p) level. Figure 2 shows the structures of H2 bound to GR-Na (n = 1–6). H2 is bound to Na with a side-on structure when n = 1, in which the two hydrogen atoms of H2 are equivalently connected to Na (distances are almost identical: R1 = 2.445, R1′ = 2.415 Å). The GR(X)-Na-H2 (center-of-mass) angle is 113.2°, which indicates that the bound structure is bent. The distance (h) between Na and GR is 2.262 Å, which is slightly elongated from that observed for GR-Na devoid of H2 (h = 2.247 Å; n = 0). The second H2 molecule, (H2)2 is bound to Na with a similar side-on arrangement when n = 2; (H2)1 and (H2)2 are bound in a similar to each other. The third and fourth H2 molecules are similarly bound to Na when n = 3 and 4. The average H2-Na distances were calculated to be 2.262, 2.436, 2.456, and 2.502 Å for n = 1–4, respectively, which indicates that the distance increases slightly with increasing number of H2 molecules (n). The fifth H2 molecule, (H2)5, binds to Na in a manner orthogonal to the surface (vertical in Figure 2) when n = 5, with a distance of 2.833 Å, which is longer than those of (H2)1–4; clearly, the first coordination shell is saturated at n = 4. The sixth H2 molecule interacts with a H2 molecule in the first coordination shell and is not directly bound to Na (the distances between the sixth H2 molecule and Na and the nearest H2 molecule are 5.037 and 3.625 Å, respectively. Larger clusters (n = 7–12) were also optimized. Side-on coordination structures were observed in all cases.


Figure 2. CAM-B3LYP/6-311G(d,p)-optimized structures of GR-Na (atom)-(H2)n (n = 1–6).
Similar binding structures were obtained for Na+, in which inner-shell H2 molecules bind to GR-Na+ in side-on orientations.
To understand these binding structures in more detail, the distances between the hydrogen atoms in H2 and the Na atom, R(Na-H) are plotted as functions of the number of H2 molecules (n) (Figure 3). The R(Na-H) distance is 2.445 Å (1st shell) when n = 1, and all hydrogen atoms are located at similar distances from Na up to n = 4, although the distance increased slightly with increasing n (2.415 Å for n = 1; 2.482 Å for n = 4). In contrast, the fifth H2 (n = 5) is much further away from Na (2.833 Å) (2nd shell) compared to the others (n = 1–4; 2.45 Å), indicating that the first coordination shell is saturated by four hydrogen molecules (n = 4). The fifth H2 binds to Na in an orthogonal direction and is located in a pocket composed of the other four H2 molecules ((H2)1–4). The second coordination shell is saturated at n = 5; hence, the sixth hydrogen molecule, (H2)6, binds to GR-Na-(H2)5 as a ligand in the third coordination shell. The distances associated with n = 6–12 clearly reveal that the second coordination shell consists of only one H2 molecule, (H2)5 and is saturated at n = 5, with the third coordination shell beginning at n = 6.
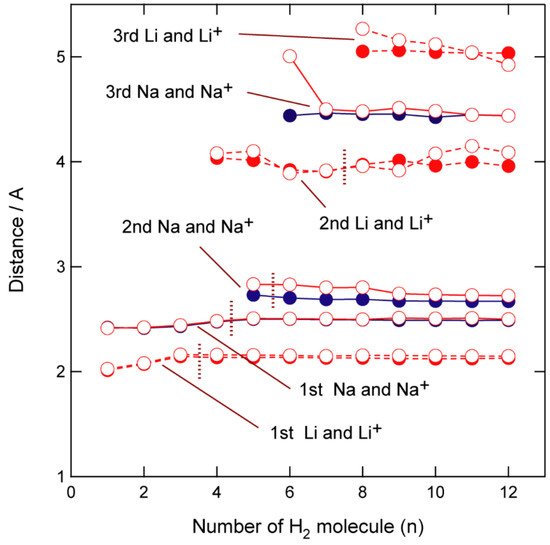

Figure 3. CAM-B3LYP/6-311G(d,p)-calculated M-H interatomic distances in GR-M-(H2)n (n = 1–12, M = Li, Li+, Na, and Na+) as functions of the number of H2 molecules (n).
The analogous distances in GR-Li+-(H2)n (n = 1–12) are shown in Figure 3. The H2 coordination structures in GR-Li-H2 are different to those in GR-Na-H2; when n = 4, the Na-H2 distance results in a large binding energy for GR-Na-H2.
2.3. Electronic States
The NPA-determined charges on Na, GR, and H2 (summation of molecular charges over all H2 molecules) are plotted in Figure 4 as functions of n. The Na and GR charges were calculated to be +0.978 and −0.978, respectively, when n = 0 (without any H2 molecule), which indicates that the unpaired electron of Na is fully transferred to GR, and that the electronic state can be expressed as (Na)+0.98-(GR)−0.98. The charges on Na were determined by NPA to be 0.953, 0.834, 0.707, and 0.707 for n = 1, 3, 5, and 6, respectively, which indicates that the charge decreases linearly to n = 5 and is then saturated. In contrast, the (H2)n charge was observed to increase to n = 5 and saturate. The electrons of H2 are gradually transferred into Na when H2 is added to GR-Na in a stepwise manner (to n = 5). A similar electron-transfer trend was observed for GR-Li to n = 3. The first coordination shells of Na and Li contain four and three H2 molecules, respectively, and electron transfer from H2 to Na (or Li) occurs only in the first coordination shell.
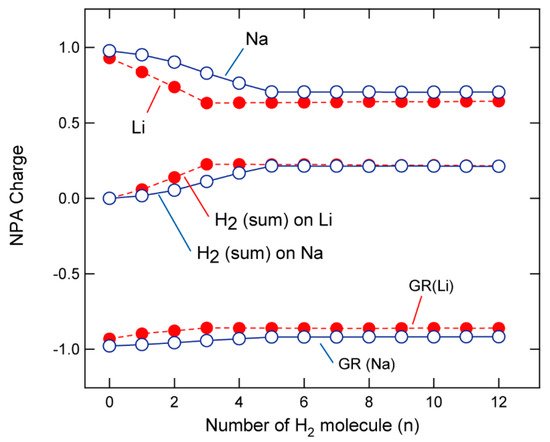

Figure 4. NPA-determined atomic charges of Li, Na, and GR as functions of n. Summed H2 charges are also plotted. Calculations were performed at the CAM-B3LYP/6-311G(d,p) level.
Distance (h) between Na and the GR surface are plotted in Figure 5 as functions of n; h was observed to increase with increasing n for both Na and Na+ to the second shell (n = 5) and became saturated at 2.35 Å (Na) and 2.42 Å (Na+). For lithium, the saturated distances were determined to be 1.85 Å (Li) and 1.89 Å (Li+) (from n = 5).
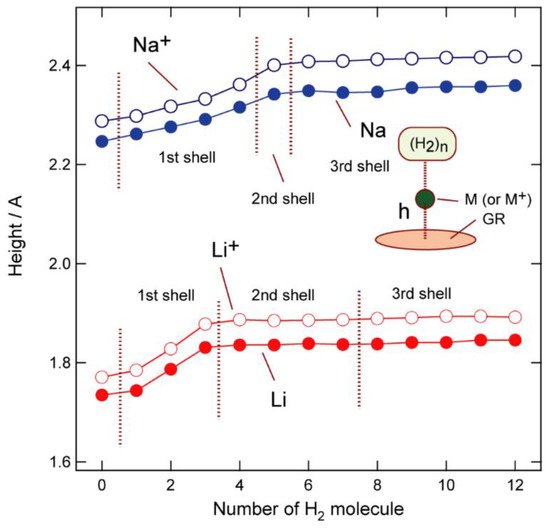

Figure 5. Distances between M and the GR surface (in Å) as functions of n (M = Li, Li+, Na, and Na+).
The Na and Li atoms are always closer to the surface than their corresponding ions (Na+ and Li+). Electrons are transferred from M to GR to form separate M(+1.0)-GR(−1.0) electronic states in the GR-M (atom) systems. Significant attractive interactions (positive-negative) operate in these GR-M systems that result in shorter M(h) distances.
2.4. H2 Binding Energies to GR-Na
The binding energy of H2 to GR-Na (per H2 molecule) is plotted in Figure 6 as a function of n. The binding energy associated with the addition of the first H2 molecule to GR-Na was calculated to be 2.72 kcal/mol (n = 1), which gradually decreased with increasing n; binding energies of 2.67, 2.50, 2.34, and 2.01 kcal/mol were calculated for n = 2–5, respectively. On the other hand, binding energies of 3.83, 3.29, 2.85, 2.20, and 1.83 kcal/mol were calculated for Li (n = 1–5, respectively), which reveals that GR-Li interacts more strongly with H2 than GR-Na for n = 1–3, while the interactions are comparable for both Li and Na at n = 4. GR-Na interacts slightly more strongly with H2 in the larger systems (n = 5–12). Thus, GR-Na appears to have a higher H2-storage ability than GR-Li.
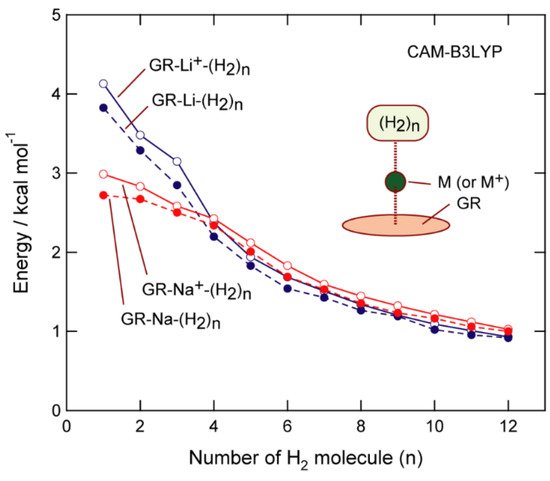

Figure 6. CAM-B3LYP/6-311G(d,p)-calculated H2-GR-M binding energies (per H2 molecule) plotted as functions of n (M = Li, Li+, Na, and Na+).
The abovementioned trends strongly suggest that GR-Na can be used as an H2-storage material; this system can store H2 up to the second coordination shell (n = 12) when a threshold binding energy of 1.0 kcal/mol is assumed. The GR-Na+-(H2)n system exhibited similar features. Since the Na-(H2)n binding energy is close to zero in the absence of GR, GR clearly enhances binding through electron transfer from Na to GR: GR + Na → (GR)−-Na+.
H2-GR-Na+ and H2-GR-Li+ binding energies are compared in Figure 6. The binding energy of the first addition of H2 to GR-Li was calculated to be 2.99 kcal/mol (n = 1), and gradually decreased with increasing n, with values of 2.58, 2.12, and 1.60 kcal/mol determined for n = 3, 5, and 7, respectively, for the GR-Na+-H2 system, and 2.58, 2.12, and 1.00 kcal/mol for the GR-Li+-H2 system, respectively.
These results suggest that GR-Na is a suitable candidate for the efficient storage of hydrogen gas for various applications. The effectivity in GR-Na is originated from the number of first coordination shell of H2: the first coordination shell in GR-Na is saturated by n = 4, which is larger than GR-Li (n = 3). Hence, GR-Na binds strongly to H2 as average.
2.5. Effect of the Functional on Biding Energy
The effect of the DFT functional on the binding energy is examined in this section, with the PW91PW91 functional [25] used for the GR-Na, GR-Na+, GR-Li, and GR-Li+ systems. The binding energies of H2 to these systems are plotted as functions of n, the results of which are shown in Figure 7. H2 is bound more strongly to the GR-Li and GR-Li+ systems than the Na systems in the n = 1–4 range using the PW91PW91 functional, whereas the opposite trend was observed for n = 5. These features are in excellent agreement with those observed using the CAM-B3LYP functional, suggesting that the present system shows only minor functional dependence.


Figure 7. Functional dependency of the H2-GR-Li+ (Na+) binding energy (per H2 molecule). Calculations were performed at the PW91PW91/6-311G(d,p) level.
References
- Lempert, R.J. Climate Change Risk Measuring Global Climate Risk. Nat. Clim. Chang. 2021, 11, 805–806.
- Rudd, J.A. From Climate Change Ignorant to Climate Change Educator. Chem. Eur. J. 2021, 27, 6107–6111.
- Merino, J.G. Climate Change. Neurology 2021, 97, 657.
- Unruh, C.F. Letting Climate Change. J. Am. Philos. Assoc. 2020, 7, 368–386.
- Fuglie, K. Climate Change Upsets Agriculture. Nat. Clim. Chang. 2021, 11, 294–295.
- Hanna, R.; Victor, D.G. Marking the Decarbonization Revolutions. Nat. Energy 2021, 6, 568–571.
- Alent’ev, A.Y.; Volkov, A.V.; Vorotyntsev, I.V.; Maksimov, A.L.; Yaroslavtsev, A.B. Membrane Technologies for Decarbonization. Membr. Membr. Technol. 2021, 3, 255–273.
- Bandelow, N.C.; Hornung, J.; Schröder, I.; Vogeler, C.S. Decarbonization and Climate Change. Rev. Policy Res. 2021, 38, 754–756.
- Stephenson, J.R.; Sovacool, B.K.; Inderberg, T.H.J. Energy Cultures and National Decarbonisation Pathways. Renew. Sustain. Energy Rev. 2021, 137, 110592.
- Shimoda, Y.; Sugiyama, M.; Nishimoto, R.; Momonoki, T. Evaluating Decarbonization Senarios and Energy Management Requirement for the Residential Sector in Japan through Bottom-Up Simulations of Energy End-Use Demand in 2050. Appl. Energy 2021, 303, 117510.
- Chiaramonti, D.; Talluri, G.; Vourliotakis, G.; Testa, L.; Prussi, M.; Scarlat, N. Can Lower Carbon Aviation Fuels (LCAF) Really Complement Sustainable Aviation Fuel (SAF) towards EU Aviation Decarbonization? Energies 2021, 14, 6430.
- De Silvestri, A.; Stendardo, S.; Della Pietra, M.; Borello, D. Decarbonizing Cement Plants via a Fully Integrated Calcium Looping-Molten Carbonate Fuel Cell Process: Assessment of a Model for Fuel Cell Performance Predictions under Different Operating Conditions. Int. J. Hydrogen Energy 2021, 46, 14988–15007.
- Guo, Z.; Wei, W.; Chen, L.; Zhang, X.; Mei, S. Equilibrium Model of a Regional Hydrogen Market with Renewable Energy Based Suppliers and Transportation Costs. Energy 2021, 220, 119608.
- Vijayakumar, V.; Jenn, A.; Fulton, L. Low Carbon Scenario Analysis of a Hydrogen-Based Energy Transition for On-Road Transportation in California. Energies 2021, 14, 7163.
- Lobo, R.; Alvarez, N.; Shanov, V. Hydrogen Nanometrology in Advanced Carbon Nanomaterial Electrodes. Nanomaterials 2021, 11, 1079.
- Lobo, R.; Ribeiro, J.H.F.; Inok, F. Hydrogen Uptake and Release in Carbon Nanotube Electrocatalysts. Nanomaterials 2021, 11, 975.
- Wu, R.; Zhang, X.; Liu, Y.; Zhang, L.; Hu, J.; Gao, M.; Pan, H. A Unique Double-Layered Carbon Nanobowl-Confined Lithium Borohydride for Highly Reversible Hydrogen Storage. Small 2020, 16, 202001963.
- Yadav, S.; Tam, J.; Singh, C.V. A First Principles Study of Hydrogen Storage on Lithium Decorated Two Dimensional Carbon Allotropes. Int. J. Hydrogen Energy 2015, 40, 6128–6136.
- Moon, H.S.; Lee, J.; Kwon, S.; Kim, I.T.; Lee, S.G. Mechanisms of Na Adsorption on Graphene and Graphene Oxide: Density Functional Theory Approach. Carbon Lett. 2015, 16, 116–120.
- Zhu, Z.H.; Lu, G.Q. Comparative Study of Li, Na, and K Adsorption on Graphite Using ab Initio Method. Langmuir 2004, 20, 10751–10755.
- Dimakis, N.; Salas, I.; Gonzales, L.; Vadodaria, O.; Ruiz, K.; Bhatti, M.I. Li and Na Adsorption on Graphene and Graphene Oxide Examined by Density Functional Theory, Quantum Theory of Atoms in Molecules, and Electron localization Function. Molecules 2019, 24, 754.
- El Kassaoui, M.; Houmad, M.; Lakhal, M.; Benyoussef, A.; El Kenz, A.; Loulidi, M. Hydrogen Storage in Lithium, Sodium and Magnesium-Decorated on Tetragonal Silicon Carbide. Int. J. Hydrogen Energy 2021, 46, 24190–24201.
- Tachikawa, H.; Iyama, T. Mechanism of Hydrogen Storage in the Graphene Nanoflake-Lithium-H2 System. J. Phys. Chem. C 2019, 123, 8709–8716.
- Tachikawa, H.; Izumi, Y.; Iyama, T.; Azumi, K. Molecular Design of a Reversible Hydrogen Storage Device Composed of the Graphene Nanoflake-Magnesium-H2 System. ACS Omega 2021, 6, 7778–7785.
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539.
More
