Location-Based Social Networks: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Fernando Ferri and Version 1 by Patrizia Grifoni.

There are several definitions for “geosocial network” or “location-based social network”: the first formal definition was given by Quercia et al. in 2010, who defined it as “a type of social networking in which geographic services and capabilities such as geocoding and geotagging are used to enable additional social dynamics”. One year later, Zheng refined this definition by stating that “a location-based social network (LBSN) does not only mean adding a location to an existing social network so that people in the social structure can share location embedded information but also consists of the new social structure made up of individuals connected by the interdependency derived from their locations in the physical world as well as their location-tagged media content, such as photos, video, and texts”. In 2013, Roick and Heuser defined LBSNs simply as “social network sites that include location information into shared contents”. Finally, one most recent definition is given by Armenatzoglou and Papadias and is the following: “geosocial network (GeoSN) is an online social network augmented by geographical information”.

  • location-based social networks
  • geosocial networks
  • geosocial query processing

1. Definitions of LBSN or Geosocial Networks

There are several definitions for “geosocial network” or “location-based social network”: the first formal definition was given by Quercia et al. [1] in 2010, who defined it as “a type of social networking in which geographic services and capabilities such as geocoding and geotagging are used to enable additional social dynamics”. One year later, Zheng [2] refined this definition by stating that “a location-based social network (LBSN) does not only mean adding a location to an existing social network so that people in the social structure can share location embedded information but also consists of the new social structure made up of individuals connected by the interdependency derived from their locations in the physical world as well as their location-tagged media content, such as photos, video, and texts”. In 2013, Roick and Heuser [3] defined LBSNs simply as “social network sites that include location information into shared contents”. Finally, one most recent definition is given by Armenatzoglou and Papadias [4] and is the following: “geosocial network (GeoSN) is an online social network augmented by geographical information”.
From the above definitions, it is evident that the peculiarity of LBSNs is the coupling of geographical information/services with social network sites that allow LBNS users to benefit from the communication and sharing functionalities provided by social networks, enhanced with geographic positions of users to locate contents, people, and activities in a physical space.
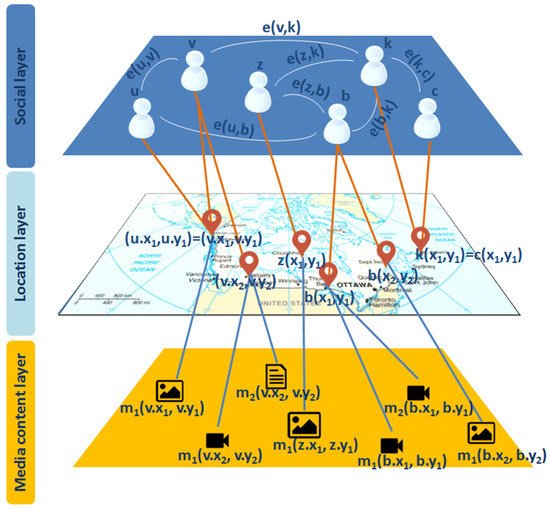
To model both the social and geographical relationships in it, a LBSN is often represented through a multilevel geosocial model, with a geosocial graph G(V, E); i.e., an undirected graph with vertex set V and edge set E. Each vertex v ∈ V represents a user and has one or more spatial locations (v.xi, v.yi) with 1 ≤ i ≤ n in the two-dimensional space associated with the n locations visited by the corresponding user, and has one or more geo-located media content mj(v.xi, v.yi) with 1 ≤ j ≤ p associated to the ith location visited by the corresponding user. Each edge e = (u, v) ∈ E denotes a relationship (e.g., friendship, common interest, shared knowledge, etc.) between two users v and u ∈ V. A graphical representation of a geosocial graph G(V, E) representing an LBSN is given in Figure 1. Three layers can be differentiated, as also suggested by Gao and Liu [5]. The first layer, named social layer, contains the users of the LBSN and the relationships among them. The second layer, named location or geographical layer, consists of the geographical information in the two-dimensional space associated with the locations visited by the users. The last layer, named media content layer, contains information about the media contents produced/shared by the users when visiting the locations.
Ijgi 11 00019 g002 550
Figure 1. Multilevel geosocial model representing an LBSN with the three layers associated.

2. The Process of Querying Geosocial Data

To process the geosocial queries, different kinds of query primitives are defined in the literature as fundamental operations that can be further combined to answer a wide range of general-purpose geosocial queries. As suggested by Saleem et al. [6], these kinds of query primitives can be grouped in three categories according to the layer of the geosocial graph that is exploited by the query primitive: social query primitives that exploit the data over the social graph, spatial query primitives that exploit the data over the spatial graph, and activity query primitives that exploit the data over the media content graph. A brief description of the query primitives used in geosocial query processing literature is provided in Table 21.
Table 21. Query primitives.
Primitive Description
Filter Removes some vertices or edges from the graph that do not satisfy a selection condition.
Partitioning
Pruning
Simplify a graph by reducing the number of edges while preserving the maximum path quality metric for any pair of vertices in the graph.
In addition to the query primitives, several basic heuristics or algorithms are applied to retrieve the geosocial data. Some examples found in the literature on geosocial querying are:
  • Best-first search algorithm: it allows to explore paths to search in the geosocial graphs by using an evaluation function to decide which among the various available nodes is the most promising to explore[7];
  • Depth-first search algorithm: it allows to explore paths to search in the geosocial graphs by starting at a given node and exploring as far as possible along each branch before backtracking [8];
Compute a partition of the vertex set into n parts of size c.
Scoring/Ranking Ranks the vertices based on a scoring function to predict the values associated with each vertex.
Sorting Re-arrange the vertices on the graph according to one or more keys.
Join Compute the join between two vertex sets if a condition defined on their features is satisfied.
Clustering Partition the vertex set into a certain number of clusters so that vertices in the same cluster should be similar to each other,
  • Dijkstra search algorithm: it allows to find, for a given source node in the geosocial graph, the shortest path between that node and every other node [9];
  • Branch and bound algorithm: it allows to explore branches of the geosocial graphs, which represent subsets of the solution set, by checking against upper and lower estimated bounds on the optimal solution and then enumerates only the candidate solutions of a branch that can produce a better solution[10];
  • Measure and conquer algorithm: it allows to explore branches of the geosocial graphs, by using a (standard) measure of the size of the subsets of the solution set (e.g., number of vertices or edges of graphs, etc.) to lower bound the progress made by the algorithm at each branching step [11].
Several query indexing approaches have also been developed in the literature to optimise the processing of geosocial queries and quickly retrieve all of the data that a query requires. Existing indexing methods can be roughly categorised into three classes: the spatial-first, the social-first, and the hybrid indexing methods. The spatial-first indexing methods prioritise the spatial factor for the index construction and then improve it with the social factor. For example, MR-Tree [12], GIM-tree [13], TaR-tree [14], and SIL-Quadtree [15] employ a spatial index (e.g., R-tree, Quad-tree, G-tree) and integrate it with the textual and social information of objects. The social-first indexing methods prioritise social relationships among objects for the index construction and then improve it with the spatial information of objects. Representatives of these methods are the Social R-tree [16], B-tree [17], and 3D Friends Check-Ins R-tree [18], which index each user along with their social relationships and then integrate the spatial information. Finally, hybrid indices are developed to store both the spatial and social information of objects giving them the same priority. For example, NETR-tree [19], CD-tree [20], and SaR-tree [21][22] encode both social information and spatial information into two major pieces of information that are used to prune the search space during the query time.

References

  1. Quercia, D.; Lathia, N.; Calabrese, F.; Di Lorenzo, G.; Crowcroft, J. Recommending social events from mobile phone location data. In Proceedings of the International Conference on Data Mining, Sydney, Australia, 13–17 December 2010; pp 971–976.
  2. Zheng, Y. Location-based social networks: Users. In Computing with Spatial Trajectories; Springer: New York, NY, USA, 2011; pp. 243–276.
  3. Roick, O.; Heuser, S. Location Based Social Networks—Definition, Current State of the Art and Research Agenda. Trans. GIS 2013, 17, 763–784. https://doi.org/10.1111/tgis.12032.
  4. Armenatzoglou, N.; Papadias, D. Geo-Social Networks. In Encyclopedia of Database Systems; Liu, L., Özsu, M.T., Eds.; Springer: New York, NY, USA, 2018; pp. 1620–1623. https://doi.org/10.1007/978-1-4614-8265-9_80714.
  5. Gao, H.; Liu, H. Data analysis on location-based social networks. In Mobile Social Networking; Springer: New York, NY, USA, 2013; pp. 165–194. https://doi.org/10.1007/978-1-4614-8579-7_8.
  6. Saleem, M.A.; Xie, X.; Pedersen, T.B. Scalable processing of location-based social networking queries. In Proceedings of the 17th IEEE International Conference on Mobile Data Management (MDM), Porto, Portugal, 13–16 June 2016; Volume 1, pp. 132–141.
  7. Pearl, J. Heuristics: Intelligent Search Strategies for Computer Problem Solving; Addison-Wesley: Massachusetts, USA, 1984; p. 48.
  8. Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 2nd Ed.; Section 22.3: Depth-first search; MIT Press and McGraw-Hill: Cambridge, Massachusetts London, England 2001; pp. 540–549. ISBN 0-262-03293-7.
  9. Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271.
  10. Land, A.H.; Doig, A.G. An automatic method of solving discrete programming problems. Econometrica 1960, 28, 497–520.
  11. Fomin, F.V.; Grandoni, F.; Kratsch, D. Measure and Conquer: Domination—A Case Study. In Proceedings of the 32nd International Colloquium on Automata, Languages and Programming, Lisbon, Portugal, 11–15 July 2005; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3580, pp. 191–203.
  12. Duan, X.; Wang, Y.; Chen, J.; Zhang, J. Authenticating preference-oriented multiple users spatial queries. In Proceedings of the 2017 IEEE 41st Annual Computer Software and Applications Conference (COMPSAC), Torino, Italy, 4–8 July 2017; Volume 1, pp. 602–607.
  13. Zhao, J.; Gao, Y.; Ma, C.; Jin, P.; Wen, S. On efficiently diversified top-k geo-social keyword query processing in road networks. Inf. Sci. 2019, 512, 813–829. https://doi.org/10.1016/j.ins.2019.10.021.
  14. Sun, Y.; Qi, J.; Zheng, Y.; Zhang, R. K-Nearest Neighbor Temporal Aggregate Queries. In Proceedings of the 18th International Conference on Extending Database Technology, Brussels, Belgium, 23–27 March 2015. https://doi.org/10.5441/002/edbt.2015.43.
  15. Cao, K.; Sun, Q.; Liu, H.; Liu, Y.; Meng, G.; Guo, J. Social space keyword query based on semantic trajectory. Neurocomputing 2020, 428, 340–351. https://doi.org/10.1016/j.neucom.2020.02.130.
  16. Yang, D.N.; Shen, C.Y.; Lee, W.C.; Chen, M.S. On socio-spatial group query for location-based social networks. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China 12–16 August 2012; pp. 949–957.
  17. Attique, M.; Afzal, M.; Ali, F.; Mehmood, I.; Ijaz, M.F.; Cho, H.-J. Geo-Social Top-k and Skyline Keyword Queries on Road Networks. Sensors 2020, 20, 798. https://doi.org/10.3390/s20030798.
  18. Sohail, A.; Cheema, M.A.; Taniar, D. Geo-Social Temporal Top-k Queries in Location-Based Social Networks. In Australasian Database Conference; Melbourne, Australia, 3-7 February 2020, Springer: Berlin/Heidelberg, Germany, 2020; pp. 147–160. https://doi.org/10.1007/978-3-030-39469-1_12.
  19. Yang, Z.; Gao, Y.; Gao, X.; Chen, G. NETR-Tree: An Eifficient Framework for Social-Based Time-Aware Spatial Keyword Query. arXiv 2019. arXiv:1908.09520.
  20. Li, Q.; Zhu, Y.; Yu, J.X. (2020, April). Skyline Cohesive Group Queries in Large Road-social Networks. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020; pp. 397–408.
  21. Li, Y.; Chen, R.; Xu, J.; Huang, Q.; Hu, H.; Choi, B. Geo-Social K-Cover Group Queries for Collaborative Spatial Computing. IEEE Trans. Knowl. Data Eng. 2015, 27, 2729–2742. https://doi.org/10.1109/tkde.2015.2419663.
  22. Li, Y. Efficient Group Queries in Location-Based Social Networks; Semantic Scholar: 2016.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
ScholarVision Creations
Feedback