Distribution Measurement Technologies: Comparison
View Latest Version
Please note this is a comparison between Version 2 by Catherine Yang and Version 1 by Antonio E. Saldana-Gonzalez.

The integration of advanced measuring technologies in distribution systems allows distribution system operators to have better observability of dynamic and transient events. In this work, the applications of distribution grid measurement technologies are explored in detail. The main contributions of this review are the review of the most recent applications of micro-Phasor Measurement Units, Smart Meters, and Power Quality Monitoring devices used in distribution systems, considering different novel methods applied for data analysis; In addition, this work derives an input-output table that relates measured quantities from micro-Phasor Measurement Units and Smart Meters needed for each specific application found in this extensive review. 

  • advanced measuring devices
  • micro-phasor measurement units
  • power quality monitors
  • smart grid technologies
  • smart meters

1. Introduction

The integration of advanced measuring technology, such as Smart Meters, micro-Phasor Measurement Units (PMUs), and Power Quality Monitors (PQM) in distribution systems, allows distribution system operators to have better observability of the electrical distribution system. High-precision measurements, rapid communication, and remote storage of the extracted data are some of the characteristics of these measuring devices.

The urgent reason to enhance the observability with the deployment of new technology devices is mainly driven by the increasing integration of distributed energy resources (solar energy, wind energy, bio-energy) and flexible loads (electric vehicles and air conditioning systems) in distribution grids. These devices have a significant effect on the operation, stability, and quality of energy distribution networks. Customers are able to exchange active power with the electric grid in two-way directions, increasing the complexity and uncertainty of the distribution system operation [1,2,3][1][2][3].

Recent works have reviewed the general applications of measurement technologies in distribution systems. In Reference [4,5][4][5], the authors described the technology architecture used in smart grids, including the metering and communication systems for transmission and distribution systems. In Reference [6,7][6][7], the authors presented an overview of measurement technology, including smart meters, smart sensors, smart power meters, Phasor Measurement Units (PMUs), Phasor Data Concentrators (PDCs), and Supervisory Control And Data Acquisition (SCADA) systems, for monitoring, protection, and control in smart grid networks. However, none of these overviews mentioned the required data characteristics for each application or the types of measuring devices used for distribution systems.

Relevant overviews of PMUs applications for distribution grids were described in Reference [8[8][9][10][11],9,10,11], which include monitoring, diagnostic, and control applications. In fact, these papers have not reviewed recent research work related to μPMUs data applications. In recent reviewed papers [12[12][13],13], authors have focused on PMUs applications, including state awareness, event detection, adaptive protection, and network reconfiguration. However, these reviews do not include a list of PMUs applications based on the input data, methods, and visualization of each application.

Furthermore, several review papers have studied the applications of smart meter data for distribution networks [14,15,16,17][14][15][16][17]. In Reference [14], the authors reviewed the smart meter data techniques and methodologies developed for different applications. They also discussed the big data issues, the transition of energy systems, data privacy, and security. In Reference [15], the authors reviewed the methods and techniques for using smart meter data, such as forecasting, clustering, classification, and optimization. However, these works do not mention the data inputs necessary to implement each of these methods.

Some research papers have studied power quality applications. Reference [18] [18] analyzed the harmonic impact of the integration of renewable sources into the distribution network. Some other recent applications are for optimal location of PQM in distribution systems, due to the limitation of measuring devices [19]. The development of optimal placement techniques and energy data are discussed in Reference [20,21,22,23,24][20][21][22][23][24]. To the best knowledge of the authors, this is the first time that a work integrates an overview of the applications of PQM for distribution systems. In this review the main contributions are:

  • A review of the most recent applications of micro-Phasor Measurement Units, Smart Meters, and Power Quality Monitoring devices used in distribution systems, considering different novel methods applied for data analysis.

  • An input-output table that relates the measured quantities from micro-Phasor Measurement Units and smart meters needed for each specific application found in this review. 

2. Distribution Measurement Technologies: Application of Data

In this section, a review of recent applications and techniques used for data processing ofμmimicro-PMUs, smart meters, and PQM devices is shown, based on a literature review of the last four years. In addition, few relevant articles were considered due to their high impact of the research over the last few years. Figure 1 summarizes the overall groups of applications found in this work, considering only three advanced measurement devices (Micro-PMUs, Smart meters, and PQMs). It is important to mention that each measurement device work with different resolutions; therefore, the applications are also oriented to monitoring events with the same time response.

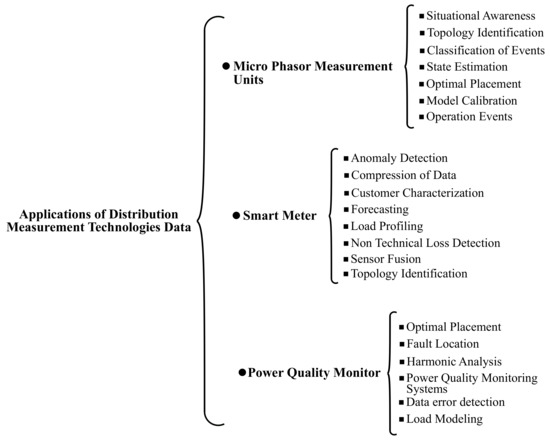
Energies 13 03730 g005 550

Figure 1.

Applications of Distribution Measurement Technologies.

42.1. Micro-PMU Data Applications

Recent applications of micro-PMU data are shown in this subsection. Table 1 shows a general summary of the applications, methods and input data found in more than 25 articles. A total of eight application groups were obtained, and two large groups can be highlighted, situational awareness and state estimation. These two groups require a high sampling rate of the measured data in order to visualize transitory events in the distribution network. Table 2 lists the input data (Micro-PMUs measurements) required for each specific application. Most of the described methods are based on synchronized current and voltage phasors (magnitude and phase) to identify, analyze, and monitor possible failures in the distribution network. A brief description of each of these application groups and methods found for data analysis is provided below.

 

Table 1. Recent application groups of  micro-PMU 

Recent application groups of  micro-PMU data.

PMU
Data.
 
Application

Group		 Input Data Methods Output Visualization Year

(Reference)		 Real Micro-PMU Data? Simulation Data?


2. 2017
[
51
]
1. Yes

2. Yes 1. No

2. No
 
Table 32. Specific applications of Micro-PMU data.

Specific applications of Micro-PMU data.

Micro-PMU Data Specific Applications in Distribution Network
3 Ph-I (Phasors): Analysis of Transient Load Behaviors [91]Analysis of Transient Load Behaviors [50]    
3 Ph-Currents (Phasor) &

Y (Admitance matrix): Optimal number and localization of micro-PMU in buses [84,89] 

Optimal number and localization of micro-PMU in buses [43]

][52] proposed a data driven approach based on the projection of a norm tren vector in to a topology library. This method was able to detect over 32 possible topology scenarios in a distribution grid.

Classification of Events: The classification of disturbing events is responsible for quantifying abnormal events that occur in the system. Recent approaches of event classification have been explored. In Reference [68][26], the authors proposed the multi-class Support Vector Machine (SVM) method to classify abnormal events based on large volumes of data. A total of 1.2 billion real measurements of two micro-PMU installed in a distribution feeder were analyzed to evaluate their actual performance, and were validated with two different methods (K-Nearest Neighbor (k-NN) and Decision Tree (DT)). The results showed that the proposed technique can accurately identify a total of 10,700 events, outperforming the other two evaluated techniques. A neural network approach was proposed in Reference [81][40], using autoencoders along with soft-max classifiers to distinguish two disruptive events. The performance of the algorithm was tested to identify if a capacitor bank switching has a normal load change or if it has a malfunctioned switching. In Reference [82][41], authors proposed two different algorithms to classify disruptive events in distribution networks. The first algorithm was based on a hybrid combination of Principle Component Analysis (PCA) together with a multi-class SVM, and the second algorithm was with an auto-encoder along with soft-max classifier. Validation results showed the superiority of the second algorithm over the first algorithm in term of accuracy. The data for training and testing was simulated in the IEEE 13-bus distribution system.

State Estimation (SE): Distribution system state estimation (DSSE) is the minimum set of variables that can be used to describe the dynamic behavior of the system, advanced measurement devices are useful to quantify these variables. In Reference [83][42], the authors proposed a decentralized state estimator to improve the operating privacy in active distribution networks and microgrids. In this work, the iterative procedure based on quadratic programming was demonstrated, which used micro-PMUs as main inputs. The studies demonstrated a high accuracy of this proposed approach for different scenarios. In Reference [84][43], the authors proposed a regularized estimator to accurately identify the operating state of the system in a short time. This estimator operated with different measuring devices with different resolutions using data mainly from SCADA-type systems and micro-PMUs. This fusion of data allowed to provide greater robustness of the estimator to noise and less error in the estimation of states. The authors of Reference [44] [85] proposed a weighted least square-based for distribution system state estimation, in which voltages and loads are chosen as state variables to compensate insufficient real-time measurements in medium voltage distribution systems. In Reference [86][45], the authors proposed a method based on the compensation circuit theory to generate an equivalent circuit. This method was able to estimate and follow the system states when sudden load changes occurred. This method used real measurement from micro-PMUs in a distribution system. In Reference [87][46], the authors proposed a simple method to determine the state variables based on power line data and bus voltage phasors from micro-PMUs installed in a distribution network. The authors showed that the proposed method can be robust to noise measurements, high levels of distributed generation, and a reduced number of measurements. Authors in Reference [47] [88] proposed an open testbed to evaluate and compare PMU estimation algorithms accuracy under experimental conditions, considering the noise propagation in order to quantify the uncertainty contributions and their impact on the estimates of the variables.

Optimal Placement: The optimal placement of micro-PMUs aims to maximize the observability of the distribution network while minimizing investment costs. In Reference [84][43], the authors propose a D-Weighted Total Variation State Estimation (WTVSE) algorithm to estimate system states with a reduced time scale (every 15 min), considering the observations of a SCADA system and micro-PMUs. In addition, a semi-defined scheduling model was proposed to optimally locate micro-PMUs and thus improve state estimation. The results of the simulation of a 95 bus distribution network showed that this proposal presents a great accuracy in the estimation of states under a diversity of scenarios, in addition to its low computational complexity. In Reference [89][48], the authors proposed a linear programming model to optimally locate phasor measurement units in distribution networks. The aim of this model was to ensure observability during possible changes in topology by operational actions. The results obtained from a medium voltage distribution network in southern China showed that the proposed method is efficient and robust to topology changes. In Reference [67][30], a greedy search algorithm was proposed for optimal micro-PMUs placement. This algorithm uses an optimal location criterion to achieve maximum observability and therefore increase the monitoring range considering different event scenarios.

Model Calibration: Dynamic models can be calibrated based on real-time advanced measurements. This is a new field of application that promises to improve the current models. In Reference [90][49], the authors proposed a methodology to enhance the synchronous generator model, based on PMU measurements. First, the estimation of the variables (frequency, voltage, and current phasors) of the dynamic state were obtained. Then, the authors calibrated the inertia constant and the reactances of the model. Finally, the performance results were obtained under different perturbation scenarios. The authors conclude that the calibration of parameters in real time requires high accuracy of advanced measurement devices.

Operation Events: The high resolution of the micro-PMU data allows to observe the dynamics (transient) of operational events that generally occur in distribution networks, such as the reconnection of microgrids, the connection of loads, and/or the connection of capacitor banks. In Reference [91][50], the authors proposed a method to analyze the transient behaviors caused by the addition of flexible loads/generation in distribution feeders. This approach modeled the load profiles based on the collection of data from various μPMU located at the low voltage level. The authors demonstrated that it is possible to compromise network reliability if several flexible regulation resources are located on the same feeder. In Reference [92][51], the authors analyzed the switching events of a three-phase capacitor bank to determine the operational parameters and the flow of reactive energy from a capacitor. The authors conducted an experimental study based on real measurements from micro-PMUs that were installed in an electrical distribution network. The results showed that the magnitude of the transient current of the feeder depends on the initial condition and the phase angle at the time of capacitor switching.

42.2. Smart Meter Data  Applications

The following subsection describe the applications of smart meter data. The objective is to present the methods developed in recent years, based mainly on machine learning techniques for the processing, prediction and monitoring of the distribution network. Table 3 shows a summary of the applications, methods and general input/output data of 37 relevant articles published in recent years. The classification of smart meters applications were divided into eight groups; however, the most prominent groups are the forecasting group and the topology identification group. These applications are mainly used by operators to monitor and control the electrical distribution network.

Table 3.

Recent application groups of Smart Meter Data.

Application Groups Input Data Methods Output Visualization Year

(Reference)		 Real

SM Data ?		 Simulation

Data?
Anomaly Detection Load Profiles (kWh), RMS

Voltage, history data		 1. Isolation Forest

2. CCAD-SW, SVR, RF

3. Quasi-linear classifier

4. Lambda system		 Anomaly consumption detection,

data integrity assault, identification

of anomalous consumption.		 1. 2019 [93]

2. 2017 [94]

3. 2017 [95]

4.2016 [96]		1. 2019 [53]

2. 2017 [54]

3. 2017 		1. 2019 [89[55]

4.2016 		]

2. 2018 [90]

3. 2018 [91][56]

4. 2016 [92]

5. 2016 [93]

6. 2018 [94]		1. No

2. Yes

3. No

4. Yes		 1. No

2. No

3. No

4. Yes

5. No

6. No		1. Yes

2. Yes

3. Yes

4. No		 1. Yes

2. Yes
[49]

μ


3. Yes

4. Yes

5. Yes

6. Yes
Compression of Data Load Profiles (kWh) 1. Deep Learning via SCSAE

2. SAE

3. SVD

4. K-SVD, K-mean, DWT, PCA, PAA		 Storage and transmission of large

sets of power consumption data

measured by smart meters.		 1. 2020 [97]

2. 2019 [98]

3. 2017 [99]

4. 2017 [100]		1. 2020 [57]

Fault Location 3-Phase Voltage and

Current Transient,

such as Sags/Swell.		 1. Multi-hidden Markov model

2. LAMDA technique.

3. Fault distance estimation		 Locate and forecast the

presence of PQ disturbances,

and determine the fault type

on radial DS.		2. 2019 [58]

3. 2017 [59]

4. 2017 [60]		 1. 2019 [134]

2. 2007 [135]

3. 2007 [136]		1. 2019 [95]

2. 2007 [96]

3. 2007 [97]		1. Yes

2. Yes

3. Yes

4. Yes		 1. Yes

1. No

2. No

3. No

4. No
2. Yes

3. Yes 1. No

2. No

3. No		 Customer

Characterization Load Profiles (kWh),

Sociodemographic atributes

of households
Harmonic Analysis 3-phase Voltage and

Current magnitude of

harmonic distortion, Odd

harmonics, flicker, THD.		1. GBM, CART, RF, DWD, Discrimination

with Polynomial Kernel

2. Random Forests, SVM, K-nearest

Neighbors and NN

3. Discriminative multi-task relationship

learning model

4. Deep-CNN and SVM		 1. Fast Fourier Transform

2. Fourier Analysis		Unemployment prediction of

household occupants, prediction of

home-occupancy status of

households, prediction of multiple

household characteristics.

3. Fourier Analysis		1. 2020 [101]

2. 2019 [102]

3. 2019 [103]

4. 2018 [104]		1. 2020 [61]

2. 2019 [62]

3. 2019 [63]

4. 2018 [64]		 1. Yes

2. Yes

3. Yes

4. Yes		 1. No

2. No		 Describe harmonic behavior

at an individual site, as well

as at many sites across a DS

using different indices of PQ.		 1. 2017 [137]

2. 2016 [138]

3. 2016 [139]		1. 2017 [98]

2. 2016 [99]

3. 2016 [100]

3. No

4. No
1. Yes

2. Yes

3. Yes 1. No

2. No

3. No		 Forecasting
Power Quality

Monitoring SystemLoad Profiles (kWh),

Weather		 Power quality indices

(Voltage and current

sags/swells, THD, indi-

vidual harmonics, flick-

ers, etc.)		1. Extended k-means, ANN and MLR

2. ML using a Q-learning

3. LSTM Recurrent Neural Network

4. FF-ANN, NARX, DNN, Gradient

Tree Boosting and Random Forests

5. Load Ensemble Method

6. Boosting additive quantile regression

7. Conditional Kernel Density estimation		 1. Sag reporting techniques.

2. Data acquisition system.

3. Data acquisition system.

Short-Term Load Forecast in

Residential Buildings, prediction

interval of electricity cost for

different time-of-use tariffs, forecast

the aggregated load.		 4. Load Flow Algorithm Power Quality Monitoring

Projects for Distribution

Network Service Providers.		1. 2020 [105]

2. 2020 [106]

3. 2019 [107]

4. 2019 [108]

5. 2018 [109]

6. 2018 [110]

7. 2016 [111]

8. 2016 [		]

3. 2019 [67]

4. 2019 [68		112]1. 2020 [65]

2. 2020 [66]

5. 2018 [69]

6. 2018 [70]

7. 2016 		1. 2018 [65[71]

8. 2016 [72]		 ]

2. 2017 [140]

3. 2017 [141]

4. 2019 [142]		1. 2018 [101]

2. 2017 [102]

3. 2017 [103]

4. 2019 [104]		1. Yes

2. Yes

3. Yes

4. Yes

5. Yes

6. Yes

7. Yes

8. Yes		 1. No

2. No		 1. No

2. Yes

3. Yes

4. Yes

3. No

4. No

5. No

6. No

7. No

8.No
1. Yes

2. No

3. No

4. No Load Classification Load Profiles (kWh)
Data error detection Voltage and current

phasors, THD, TDD, and

short term flicker.		1. Statistical Tool

2. Deep auto-encoder and (SOM)

3. Finite Mixture Model of Gaussian

multivariate distributions

4. Constrained k-means algorithm		 Energy tariffs at different times

 1. Correlation Analysisof the day and identification

of time periods during the

season, months, etc.		 1. 2020 [ Detection and correction

error in PQ monitoring

data.		113]

2. 2020 [114]

3. 2016 [115]

4. 2016 [116]		1. 2020 [73]

2. 2020 [		 1. 2017 [14374]

3. 2016 [75]

4. 2016 		]1. 2017 [105][76] 1. Yes

2. Yes

3. Yes

4. Yes		 1. No

2. No

3. No

4. No
1. Yes 1. No Non Technical

Loss Detection Load Profiles (kWh),

Geographical information,

line parameters
Load Modeling RMS voltage and current,

Active and Reactive Power,

during disturbances on the

upstream networks.		1. Hybrid Deep Neuronal Networks

2. Deep convolutional-recurrent NN

3. Hybrid DT and SVM classifiers

4. Optimum PF, k-means, GMM,

Birch, affinity propagation and SVM		 Detection and location of

electricity thefts, irregular and

regular profiles		 1. Load parameter derivation Derive, test, and verify

the dynamic load model

parameters.		1. 2020 [110]

2. 2020 [117]

3. 2016 [118]

4. 2016 [119]		1. 2020 [70]

2. 2020 [77]

3. 2016 [78]

4. 2016 		1. 2013 [144[79] ]1. 2013 [1. Yes

2. No

3. No

4. Yes		 1. No

2. Yes

3. Yes

4. No
106] 1. Yes 1. Yes Sensor Fusion Load profiles (kWh),

currents, voltages,

admittance matrix, bus

voltage phasor, power

flows.		 1. Recurrent neural networks, and sparse

Bayesian learning for state estimation

2. Modified Dynamic Mirror Descendent

3. Mixed integer linear programming		 Locating harmonic sources,

separation of measurements in a

distribution feeder, prediction of

outage regions.		 1. 2020 [120]

2. 2020 [40]

3. 2019 [121]		1. 2020 [80]

2. 2020 [81]

3. 2019 [82]		 1. No

2. Yes

3. No		 1. Yes

2. Yes

3. Yes
Topology

Identification Load profiles (kWh), RMS

voltage (feeder and smart

meter), line parameters,

currents.		 1. Physical-probabilistic-network,

lasso regression

2. Tree-based search methodology

3. PCA and Grap Theory

4. DSTE Algorithm

5. Graphical Modeling

6. Inhouse algorithm based Voltage profile

correlation analysis		 Operation mode of distribution

networks and voltage correlations

with different buses. Topology

Estimation		 1. 2019 [122]

2. 2019 [123]

3. 2017 [124]

4. 2016 [125]

5. 2016 [126]

6. 2015 [127]		1. 2019 [83]

2. 2019 [84]

3. 2017 [85]

4. 2016 [86]

5. 2016 [87]

6. 2015 [88]		 1. No

2. Yes

3. No

4. Yes

5. Yes

6. Yes		 1. Yes

2. No

3. Yes

4. No

5. Yes

6. No
Situational

Awareness 3-Ph voltage and currents

(magnitudes and angles),

frequency, active power,

reactive power.		 1. Three stage algorithm
3-Ph-V (Phasors): Estimation of Voltage Magnitude error [84]Estimation of Voltage Magnitude error [43]


2. Dynamic WSMW

3. Generalized GLM

4. Parametric Sparsity

5. Compensation Theorem

6. CUSUM

7. Thevenin Estimation

8. LWSS

9. Experimental Analysis

10. Kernel PCA and pSVM

11. KF and Model Synthesis

12. Theoretical Analysis
Identification of swithching actions and

new topology scenarios [74,79,80]Identification of swithching actions and

new topology scenarios [28][38][52]
Voltage magnitud change, current

magnitud change, active power

change.		 1. 2020 [71]

2. 2019 [68]

3. 2019 [69]

4. 2019 [74]

5. 2018 [66]

6. 2018 [67]

7. 2018 [75]

8. 2017 [72]

9. 2017 [73]

10. 2016 [70]

11. 2016 [76]

12. 2019 [77]		1. 2020 [25]

2. 2019 [26]

3. 2019 [27]

4. 2019 [28]

5. 2018 [29]

6. 2018 [30]

7. 2018 [31]

8. 2017 [32]

9. 2017 [33]

10. 2016 [34]

11. 2016 [35]

12. 2019 [36]		 1. Yes

2. Yes

3. Yes

4. No

5. Yes

6. Yes

7. No

8. Yes

9. Yes

10. Yes

11. Yes

12. Yes		 1. No

2. No

3. No

4. Yes

5. Yes

6. Yes

7. Yes

8. Yes

9. No
 


10. No

11. Yes

12. Yes
Topology

Identification Voltage (magnitude and

phase angle)		 1. Recursive Grouping

2. Adaptive Lasso

3. TSV-Top

4. Projection of Norm tren Vector		 New switch configuration in the

3-Ph-V (Phasors) & Loads:
topology
Load and Voltage Estimation Error [85]Load and Voltage Estimation Error [44]
1. 2020 [78]

2. 2019 [74]

3. 2018 [79]

4. 2015 [		1. 2020 [80]37]

2. 2019 [28]

3. 2018 [38]

4. 2015 [39]		 1. No

 
2. No

3. No

4. No 1. Yes

 
2. Yes

3. Yes

4. Yes
Classification

of Events 3 Ph-Voltage and currents

(magnitudes & angles)		 1. Multi-class SVM

2. NN based autocoders (Softmax)

3. PCA and SVM based autocoders		 Event location and disruptive

classes		 1. 2019 [68]

3 Ph-V & 3 Ph-I (Phasors): Single and 3 phase current &

voltage event detection [69]		Single and 3 phase current &

voltage event detection
2. 2018 [81]

3. 2017 [82]1. 2019 [26]

2. 2018 [40]

3. 2017 [41]		 1. Yes

2. No

3. No
[27] Response of a PV farm (Current

and Voltage) of 3 lightning events [73].		Response of a PV farm (Current

and Voltage) of 3 lightning events [
1. No

2. Yes

3. Yes
33]. Detection of capacitor

bank switching [92]		Detection of capacitor

bank switching [51]
State

Estimation Voltages, currents, line
3 Ph-V & 3 Ph-I (Phasors):


admittances, loads.
Fault position with accuracy,

sensitivity to noise level [72]		Fault position with accuracy,

sensitivity to noise level [32]
1. WLS, WLS with NR

2. R-NESE & WTVSE

3. LSE, ARMA and SVM

4. Compensation Theorem

5. Compressive Sensing & WLS

6. DFT and WLS
Distinguishing between two disruptive events

and the normal load changing event [
Estimation of voltage magnitud,

loads, currents and errors from

actual states.		 1. 2020 [83]

2. 2020 [84]

3. 2019 [85]

4. 2018 [45]

5. 2017 [46]

6. 2018 [47]		 1. No

2. No

3. No

4. Yes

5. No

6. Yes		 1. Yes

2. Yes

3. Yes

4. Yes

5. Yes

6. Yes
82].Distinguishing between two disruptive events

and the normal load changing event [42].		 Identify event location and

disruptive classes [74,81]		Identify event location and

disruptive classes [28][40]
4. 2018 [86]

5. 2017 [87]

6. 2018 [88]		1. 2020 [42]

2. 2020 [43]

3. 2019 [44]

Optimal

Placement Voltage phasor, parameters

of the branch.		 1. Mixed Integer Semi-definite
3 Ph-V & 3 Ph-I (Phasors): Event Location and Identification [66]Event Location and Identification [29]


Programming Model

2. Integer linear programming

3. Greedy Search
Event detection of voltage sag based

on Data Index and Reconstruction Error [70].Event detection of voltage sag based

on Data Index and Reconstruction Error [34].
Optimal number and localization

of micro-PMUs at buses
Fault currents to

coordinate relays [75]Fault currents to

coordinate relays
1. 2020 [84]

2. 2019 [89]

3. 2018 [67]		1. 2020 [43]

2. 2019 [48]

3. 2018 [30]		 1. No

2. No

3. Yes		 1. Yes

2. Yes

3. Yes
[31]
Model

Calibration Frequency, voltage and

current phasors.		 1. Non-Linear Estimation Calibrated parameters
3 Ph-V & 3 Ph-I (phasors),

frequency: Estimation of sub-transient generator

model variables [90].		Estimation of sub-transient generator

model variables [49].		 Cyclic frequency trend and anomaly

signals detection [71]		Cyclic frequency trend and anomaly

signals detection [25]
1. 2020 [90]1. 2020 [49] 1. No 1. Yes
 
Operation

Events Voltage and currents

(magnitudes and angles)		 1. Fuzzy C-means

2. Data driven analysis based

on RLC Model		 Switching event, operational

3 Ph-V & 3 Ph-I (Phasors), Active

and Reactive Power, frequency: Anomaly Detection Architecture [67,68]Anomaly Detection Architecture [30][26]
parameters (real and reactive power

Optimal D-PMU placement [67]Optimal D-PMU placement [30]
flow), voltage and current (feeders

and loads)
Event Classifier of PQ

events [68]Event Classifier of PQ

events [26]
1. 2017 [91]

2. 2017 [92]1. 2017 [50]
3 Ph-V & 3 Ph-I (Phasors), loads, Y (admitance matrix): Tracking State Estimation [86,87]Tracking State Estimation [45][46]    
 

Situational Awareness:

Most of applications are driven to aware distribution operator of transient events due to the high sampling frequency and communication abilities of micro-PMUs.

μIn Reference [66], the authors proposed a method based on the compensation theorem to detect abnormal events in distribution systems. This method generates an equivalent circuit using the current and voltage phasors captured by

In Reference [29], the authors proposed a method based on the compensation theorem to detect abnormal events in distribution systems. This method generates an equivalent circuit using the current and voltage phasors captured by

μmicro-PMUs. Similarly, a cumulative sum (CUSUM) algorithm was proposed in Reference [67] to detect anomalies having limited micro-PMUs. Validation results showed the effectiveness of this algorithm to voltage, current, and active power changes in the distribution system. In Reference [68], the authors proposed the multi-class Support Vector Machine (SVM) method to detect and classify abnormal events based on large volumes of data. A total of 1.2 billion real measurements of two micro-PMU installed in a distribution feeder were analyzed to evaluate their actual performance and were validated with two different methods, which are K-Nearest Neighbor (k-NN) and Decision Tree (DT). The results showed that the proposed technique can accurately identify a total of 10,700 events, outperforming the other two evaluated techniques. In Reference [69], a generalized Graph Laplacian Matrix (GLM) to visualize different voltage and current events in a real test feeder was proposed. Moreover, a kernel principle component analysis and a partially Support Vector Machine (pSVM) was used in Reference [70] for voltage sags detection based on data index and reconstruction error. The effectiveness of these methods were tested on a real distribution network with

micro-PMUs. Similarly, a cumulative sum (CUSUM) algorithm was proposed in Reference [30] to detect anomalies having limited micro-PMUs. Validation results showed the effectiveness of this algorithm to voltage, current, and active power changes in the distribution system. In Reference [26], the authors proposed the multi-class Support Vector Machine (SVM) method to detect and classify abnormal events based on large volumes of data. A total of 1.2 billion real measurements of two micro-PMU installed in a distribution feeder were analyzed to evaluate their actual performance and were validated with two different methods, which are K-Nearest Neighbor (k-NN) and Decision Tree (DT). The results showed that the proposed technique can accurately identify a total of 10,700 events, outperforming the other two evaluated techniques. In Reference [27], a generalized Graph Laplacian Matrix (GLM) to visualize different voltage and current events in a real test feeder was proposed. Moreover, a kernel principle component analysis and a partially Support Vector Machine (pSVM) was used in Reference [34] for voltage sags detection based on data index and reconstruction error. The effectiveness of these methods were tested on a real distribution network with

μPMUs. In Reference [71], the authors proposed a Granger causality technique to analyze the frequency event propagation from the transmission network to the main feeder of a distribution network using

PMUs. In Reference [25], the authors proposed a Granger causality technique to analyze the frequency event propagation from the transmission network to the main feeder of a distribution network using

μmicro-PMUs measurements. The authors also proposed a sparse coding method to determine the spectral frequency of abnormal events. The proposed approach was tested with real-time data from a public network located in Riverside, California. In Reference [72], the authors proposed a state estimator to identify faults in distribution lines using micro-PMUs. This estimator determines the error, using a weighted residual metric. Validation tests have shown that the proposed estimator correctly detects and locates distribution line failures in presence of bi-directional flows. In Reference [73], an experimental analysis of lightening strikes was proposed using micro-PMU data collected during a day of rainstorms. The main interest of the study was to analyze the transient response of a 7.5 MW PV farm and its associated substation. Results showed the high resolution of micro-PMU to capture transients of current and voltage phasors during lightening-induced events. Reference [74] proposed a parametric sparsity method to detect and locate events from distribution grids. An optimization algorithm based on particle swarm was proposed in Reference [75] to coordinate overcurrent relays installed in microgrids and distribution networks. In addition, a technique to identify uncertainties in real-time was also proposed. Authors in Reference [76] proposed a method to synthesize steady state models for multiple-sections of active distribution networks (unbalanced) using real-time PMU data. Additionally, a Kalman filtering technique was proposed to extract the quasi-steady state components, noise filtration, and outliers from PMUs. The results from two simulated events demonstrate that the proposed technique can produce an accurate model for any feeder configuration located between PMUs installed in active distribution networks. Authors in Reference [77] evaluated the transmission characteristics of a Rogowski electronic current transformer and an electronic voltage transformer (EVT) in a simulated and real testing platform. Experiment results showed that the EVT and the traditional power transformer have similar performance in the transient process of disconnecting switch breaking. Additionally, the power transformer was not affected by temperature changes, while that in the electronic voltage transformer the temperature had a great influence impact.

micro-PMUs measurements. The authors also proposed a sparse coding method to determine the spectral frequency of abnormal events. The proposed approach was tested with real-time data from a public network located in Riverside, California. In Reference [32], the authors proposed a state estimator to identify faults in distribution lines using micro-PMUs. This estimator determines the error, using a weighted residual metric. Validation tests have shown that the proposed estimator correctly detects and locates distribution line failures in presence of bi-directional flows. In Reference [33], an experimental analysis of lightening strikes was proposed using micro-PMU data collected during a day of rainstorms. The main interest of the study was to analyze the transient response of a 7.5 MW PV farm and its associated substation. Results showed the high resolution of micro-PMU to capture transients of current and voltage phasors during lightening-induced events. Reference [28] proposed a parametric sparsity method to detect and locate events from distribution grids. An optimization algorithm based on particle swarm was proposed in Reference [31] to coordinate overcurrent relays installed in microgrids and distribution networks. In addition, a technique to identify uncertainties in real-time was also proposed. Authors in Reference[35] proposed a method to synthesize steady state models for multiple-sections of active distribution networks (unbalanced) using real-time PMU data. Additionally, a Kalman filtering technique was proposed to extract the quasi-steady state components, noise filtration, and outliers from PMUs. The results from two simulated events demonstrate that the proposed technique can produce an accurate model for any feeder configuration located between PMUs installed in active distribution networks. Authors in Reference [36] evaluated the transmission characteristics of a Rogowski electronic current transformer and an electronic voltage transformer (EVT) in a simulated and real testing platform. Experiment results showed that the EVT and the traditional power transformer have similar performance in the transient process of disconnecting switch breaking. Additionally, the power transformer was not affected by temperature changes, while that in the electronic voltage transformer the temperature had a great influence impact.

Topology Verification: Distribution networks models are often imprecise or outdated. Topology identification is essential for monitoring and control distribution systems. The micro-PMUs devices are able to extract measurements from network nodes in real-time in order to track topology changes. In Reference [78][37], the authors proposed a technique to estimate impedances through a reduced Kron matrix also called “subKron” form. Additionally, a recursive clustering algorithm was implemented to reconstruct the topology of radial networks from line impedances. The results of the simulation showed that this technique is robust to measurements with additive noise that is generally captured by micro-PMUs; however, it has limitations when applied to large distribution networks. In Reference [74][28], the authors proposed an adaptive lasso technique to identify changes in topology caused by permanent failures in distribution systems. This technique is able to locate faults geographically in real time using PMUs that capture voltage and current phasors with high accuracy. The results of this work demonstrated the efficiency of this technique in different case studies. In Reference [79][38], the authors proposed a method to detect topology changes in distribution networks based on the Time-Series Signature Verification (TSV) method. This method considers the relationship that occur when there are changes in network topology. Validation results showed that the proposed method works satisfactorily with the partial knowledge of the state of the network. Authors in Reference [80

Anomaly Detection: Anomaly detection techniques are useful to detect abnormal conditions in smart meters data, such as suspicious consumption, missing data, or unplanned events. In Reference [93][53], authors proposed an algorithm based on isolation forest to detect the presence of anomalies in smart grid using non-labeled data. Authors also used a Principal Component Analysis (PCA) to compress the volume of data in a distribution system. In Reference [94][54], authors implemented a support vector regression with a random forest method using sliding windows, to identify anomalous consumptions of real-world data. In Reference [95][55], the authors developed an anomaly detector system, capable of analyzing smart meter measurements from a data concentrator in near real-time. The design of this system can detect abnormal conditions at medium and low voltage levels using a quasi-linear classifier. Reference [56] [96] proposed a technique with a Lambda architecture to detect anomalies. This technique was based on real-time consumptions that were analyzed through supervised learning. Additionally, a threshold index for the detection of suspicious consumption was considered. The evaluation of this algorithm in real scenarios demonstrated its effectiveness and precision in detecting anomalies.

Compression of Data: Data compression techniques help to reduce the volume of data collected from advanced measurement devices; they also help to improve the transmission speeds from multiple measurement points. In Reference [97][57], the authors proposed a deep learning technique with a convolutional dispersion auto-encoder for data compression. This method keeps more information than Singular Value Decomposition (SVD) and PCA methods, at the same coding speed, preserving details of the original power, and the calculation times are lower. In Reference [98][58], the authors proposed a neural network based on an automatic encoder to compress household consumption data in a distribution network. This proposed encoder must be installed on the user’s side to compress the smart meter readings. Compared to some existing linear compression models, such as PCA, DWT, and SVD, the SAE compressor has lower % errors according to a study carried out with real data from China and Ireland. Similarly, in Reference [99][59], a methodology using the SVD technique for data compression was presented. This methodology was used in a test system with data from different substations of a UK company. This technique achieves a significant reduction in the volume of data to be transmitted, with minimal error in its reconstruction. Reference [60] [100] proposed a SVD sparse coding technique to compress smart meter data. This dispersion technique extracts the information using linear combinations from load clusters. The results obtained comparing 4 techniques showed that the proposed technique obtains the least loss of information.

Customer Characterization (Socio-demographic): Predictive analysis can also be applied to determine the characteristics of network consumers, for example, predicting the number of unemployed people, number of occupants in a building and/or predicting daily household activities. In Reference [101][61], authors compared six machine learning models to determine the number of unemployed people in a household. The overall results showed that the most accurate models were the multi-layered perception and distance-weighted discrimination aproach. Similarly, in Reference [104][88], a neural model was proposed to determine the employment situation of consumers. This type of information can help governments to reduce unemployment levels and also help to improve their economy. In Reference [102][62], the authors implemented a genetic algorithm to identify the number of occupants in a residential building using smart meter data. Validation results showed that this algorithm can optimally predict the number of occupants in households. In Reference [103][63], an automatic learning model was proposed to identify characteristics of residential occupants, e.g., people living in the household, average age, and daily activities in the household, from the daily electricity consumption of the users. The validation of this model was implemented in a real distribution network in Ireland, in which technical characteristics allow obtaining this information.

Forecasting: The optimal generation planning requires that operators have tools to predict demand growth in a short and medium terms. In recent years, techniques based on machine learning have been developed, considering multiple variables in the prediction models, including electricity consumption, weather conditions, electricity tariff costs, and population growth that contributes to generate accurate prediction models. In addition, with the growing technological development, it is possible to concentrate all this data in real time, which allows the parameters of the models to be systematically updated. In Reference [106][66], the authors designed a short-term prediction model based on a Q-learning scheme that used meteorological data and smart meters as input variables. This scheme was composed of ten deterministic prediction models and four probabilistic heuristic models which were selected based on their accuracy. The results presented demonstrate a higher accuracy of Q-learning predictions than traditional approaches. In Reference [105][65], an artificial neural network with a multiple regression technique was proposed to predict load consumption using temperature and solar irradiation variables in the model to obtain more accurate predictions. The validation of this proposal was demonstrated in a real data set of smart meters that included photovoltaic generation. In Reference [107][67], the authors proposed a recurrent neural network technique to predict consumption in short-term scenarios. This proposed approach was tested on a public data set on real residential consumption and compared with other techniques for validation. In Reference [108][68], the authors proposed a Nest-Bcktr algorithm for short-term load forecasting. A comparison between other six machine learning algorithms were made, in terms of RMSE indices and absolute errors. The validation was programmed in Python using a 2-year data set from smart meters. The results showed that this proposed algorithm predicts consumption with lower errors. In Reference [109][69], a load ensemble method to forecast aggregated loads was proposed. This method produces multiple training and prediction models with different sub-profiles. In addition, a weighted optimization is used to combine and determine the best prediction. In Reference [111][71], an additive regression model was proposed to forecast the distribution of electricity consumption added to the network. This model generates different probability scenarios that help operators to plan and operate the network in the future. In Reference [112][72], the authors used a method based on kernel density estimation to forecast future growth of electricity consumption. This method considered predictions of electricity costs for different tariffs, which means potentially important savings for users.

Load Classification: Refers to the grouping of electrical consumption including residential, commercial and industrial loads. In recent years, various grouping techniques have been proposed with data from smart meters that have provided useful information to distribution system operators. In Reference [113][73], electricity consumption and energy tariff variability were analysed in four different seasons. In this analysis, several statistical tools were applied to analyze different energy consumption’s using real data from smart meters. The study showed that users consume more energy when they do not know the variability of energy costs. The authors recommended that consumers learn about tariff dynamics in order to minimize energy consumption costs. In Reference [114][74], the authors proposed a prediction technique based on a trained auto-encoder that analyzed smart meter data and also grouped them using a self organizing map. In Reference [115][75], a finite mixture model based on a variant Gaussian distribution to identify non-typical behavior in the distribution system was proposed. This model classified different customer profiles according to their load levels and variability. In Reference [116][76], the authors proposed a k-means clustering algorithm for phase identification of interconnected customers in the network. This algorithm uses as inputs the voltage signals from smart meters and SCADA measurement system. The test results obtained from a distribution network in California showed that the algorithm has an overall accuracy above 90%.

Non-technical loss detection: Detection of non-technical losses are basically electricity theft consumers, faulty meters or billing errors. In Reference [110][70], a hybrid deep neuronal network to detect non-technical losses in smart meters was proposed. This algorithm was tested with real smart meter data from the largest electric utility in Spain. Validation results showed the accuracy of this aproach to identify anomalies in distribution systems. In Reference [117][77], the authors proposed a deep convolutional neural network to detect non technical losses in distribution grids. This approach detected manipulations of consumer energy readings that falsely overloaded the power company. The results obtained in this work indicate that the fusion of multiple data, including smart meters, SCADA systems, and meteorological reports, contributes to the accurate detection of energy theft consumers. Reference [118] [78] proposed a methodology based on the hybrid combination of decision tree and support vector machine classifiers to detect fraudulent consumption. In Reference [119][79], the authors proposed a classifier based on the optimal-path forest algorithm to detect anomalies and non-technical losses in distribution networks. This machine learning technique requires training from regular consumer profiles in order to generate a sample group base, and, when a new consumer connects with irregular profiles, he is automatically identified. Validation results showed that this technique is robust and accurate for classifying different types of consumers.

Sensor Fusion: Sensor fusion is the integration of data from smart meters with other measurement devices and is intended to improve the observability and accuracy of monitoring distribution systems. In Reference [120][80], the authors proposed a state estimator to identify harmonic sources in an unbalanced distribution system. The state estimator was based on neural networks and Bayesian learning, and the input signals were captured by smart meters and micro-PMUs. Validation results showed the high accuracy of the estimator even in presence of distributed generation. In Reference [40][81], the authors proposed an algorithm to disaggregate loads from a distribution feeder into N components. The main objective was to separate network losses and reactive power injections from capacitors. This algorithm was based on a learning aproach and used multiple measurement sensors to determine the technical feasibility of separation. Validation results indicate that data fusion of reactive power measurements in the algorithm can improve the accuracy in the prediction of the network behavior up to 32%. In Reference [121][82], the authors proposed a mixed integer linear programming algorithm to determine fault locations and prediction of outage regions. This algorithm requires of smart meter data and remote fault indicators measurements in near real-time in order to support distribution system operation in a precise time-step.

Topology Identification: Information on the topology of the distribution network helps the operator to make optimal decisions when unexpected events occur. Authors in Reference [83] [122] proposed a physical probabilistic network model to identify the connections using voltage correlations between different buses. This method was compared with a lasso regression method. In Reference [123][84], a tree-based search methodology was proposed to approximate the missing cable information in low voltage distribution networks. In Reference [124][85], a method to identify the connectivity between load phases in distribution networks was proposed. Additionally, the presence of technical losses and some errors that may arise during measurements (missing data, synchronization) were considered. This method implemented the principal component analysis to infer the topology of the use of smart meter measurements. This method proved to be robust in the presence of distributed generation. In Reference [125][86], the authors presented an algorithm for topology estimation based on voltage measurements from smart meters. Validation results showed that 9 out of 10 of the estimates were correct in secondary circuits of a Georgia Tech distribution system, even in noisy environments. The authors mentioned that it is extremely important to have ultra-precise measurement devices for correct estimation of voltage drop based topology, especially when analyzing short lines feeding small loads. In Reference [126][87], a graphical model to identify distribution topologies based on a probabilistic relationship between different voltage measurements was proposed. Additionally, the authors proposed an expansion-tree based algorithm aimed at minimizing the Kullback-Leibler divergence in a distribution system. In Reference [127][88], an algorithm to correct connectivity errors of smart meters and meters on distribution feeders was developed. This algorithm identified the neighboring meters through a voltage profile correlation analysis.

42.3. Power Quality Monitoring  Applications

In this last section, recent applications of PQM devices are shown, considering different methods. Table 4 shows a general summary of the applications, methods, and PQM input/output data obtained from 18 articles published in recent years. The PQM applications are divided into six groups, of which the optimal placement group can be highlighted by the number of publications in recent years. One of the groups included in this table was the power quality monitoring systems, which is basically the application of PQM in the distribution network of some countries that have carried out projects to improve the quality of transported energy.

 
Table 4.

Application groups of Power Quality Monitoring Data.

Application

Group		 Input Data Methods Output Visualization Year

(Reference)		 Is It Real

PQM Data ?		 Simulation

Data?
Optimal Placement Topology of Distribution

Grid (Line parameters,

Transformers capacity,

Loads and generation).

Historic Measurement of

PQM (sag/swell, THD)		 1. TLBO Algorithm

2. Multi-objective Evolutionary

Algorithm with Tables

3. Seeker Optimization

Algorithm based on Pareto

4. Entropy-based and Bayesian

Network Model

5. PMRA Algorithm

6. WLS Method		 Optimal placement of

PQM in complex

distribution networks.		 1. 2019 [128]

2. 2018 [129]

3. 2018 [130]

4. 2016 [131]

5. 2016 [132]

6. 2018 [133]

Optimal Placement: This large application group describes some recent approaches to determine the optimal positioning of PQM, with the aim of minimizing network investment costs. In Reference [128][89], the authors implemented the TLBO algorithm to optimally locate PQMs by considering degradation in large distribution networks. The objective of this approach was to minimize the number of PQMs in order to minimize the costs of assets in the monitoring system. In Reference [129][90], the authors proposed the MEAT optimization algorithm to find the best locations to install advanced PQM in distribution network. This proposed approach had multiple objectives, such as minimizing monitoring investment costs, minimizing voltage drops, and maximizing system observability. The authors recommend this approach for those electricity companies that need to evaluate the investments they will make to optimally improve network observability. In Reference [130][91], authors proposed the seeker optimization algorithm to find the optimal locations of PQM devices in a 14-bus test system. The test system results showed that with few locations of the PQMs the values of the harmonic state were accurately estimated. In Reference [131][92], an optimization algorithm based on Bayesian network models was proposed. The objective was to minimize the investment costs of PQ monitoring devices and to maximize the observability of the distribution network. Evaluation results showed that this algorithm significantly reduced the uncertainty of PQ values on unsupervised feed links. In Reference [132][93], the authors proposed a probabilistic method to observe the uncertainty associated with high/low impedance faults in distribution systems. The objective was to determine the optimal location of PQM devices to maximize observability in the system. In addition, two indices were proposed in this work to quantify the robustness of distribution networks with different voltage drops. The authors in Reference [133] [94] mathematically analyzed the impact of the accuracy of state estimation (with power meters) by varying the spatial distribution and number of devices installed in the network. The objective was to minimize the number of devices to be installed and to identify the optimal location in the distribution networks, ensuring a desired accuracy in the estimation of voltage and current. The results show that the proposed mathematical framework is a useful tool for the design of optimal device placement strategies in current monitoring systems.

Fault Location: Due to the high sampling rate and precision of this device, some authors have proposed algorithms to track faults in distribution systems. In Reference [134][95], the authors proposed a PQ disturbance predictor based on a Multi-Hidden Markov Model (MHMM). This predictor analyzes large volumes of data, including local weather variables to improve forecast accuracy, and also incorporates a Hadoop system that reduces calculation times for very complex systems. The forecast of this model can be adapted to different resolutions (minutes, hours, days, or up to 3 weeks). In Reference [135][96], the authors proposed a multivariate data analysis technique to locate line failures in unbalanced distribution systems.

This technique was based on PQM devices installed in distribution substations, line parameters and the topology configuration. The authors concluded that the proposed technique benefits operators to accelerate the tasks of system restoration (permanent faults). In Reference [136][97], the authors designed a power quality software to identify and locate faults in distribution feeders. This software performs a short circuit analysis based on historic and real measurements of PQM. The validation results showed that this software has better accuracy for locating faults in distribution feeders than some commercial software.

Harmonic Analysis: These application refers to detect harmonics or abnormal behaviours in distribution system using advanced PQ devices. The authors in Reference [137] [98] presented multiple techniques to locate harmonic sources in distribution grids using PQ data. The objective was to design strategies to mitigate potential problems. Additionally, in this work a harmonic compliance index was presented, which allows to give a quick indication about violations of the permissible harmonic limit in a particular site. In addition, a graphical method based on harmonic reports showed a wide detail of harmonic performance in many sites in a compact form. The authors in Reference [99] [138] presented several digital processing techniques to detect missing or abnormal data. The validation tests were implemented in 8 German networks with residential, commercial and mixed customer loads. The authors concluded that: "The identification of useful information cannot be manual anymore and requires a comprehensive set of intelligent and automated analysis tools". Authors in Reference [139][100], compared the robustness, flexibility, and limitations of a composite bus index and an aggregate bus index. These two indices were proposed and validated in a test system to evaluate the PQ of buses installed in distribution networks. The authors concluded that these indices were closely related and it is important to provide an adequate weighting in order to have a greater flexibility between them.

Power Quality Monitoring System: Power Quality Monitoring Systems (PQMS) have been implemented in several countries to improve the power quality in distribution systems. In Reference [65][101], the authors designed a power quality monitoring software based on real-time data. This software was capable to analyze complex power quality problems using a FPGA-type hardware that worked as an independent integrated system. The authors concluded that these modern monitoring system substantially improve the life of the assets that make up the smart grids. Authors in Reference [102] [140] presented a project report of a power quality monitoring system which has been in operation in Australia since 2002. The objective of this report was to provide a general overview of the main problems found during the development of the PQMS. The authors concluded that monitoring systems with advanced measurement devices capable of providing PQ indices will rapidly increase in future power grids. Authors in Reference [103] [141] designed a PQ monitoring system for a new generation of substations located in Shanghai, China. This system was based on international communication standards that allow remote monitoring of harmonics at a frequency of 12.8 kHz. This system is capable to analyze complex power quality problems, as well as the location of harmonic sources in the distribution networks. An improved hardware/software architecture with a real-time monitoring and control system for the integration of micro grids into MV distribution networks was presented in Reference [142][104]. The proposed system is capable of estimating the power flows of the medium voltage branch by means of load power measurements and a suitable load flow algorithm. The proposed system was considered more efficient than SCADA implementation.

Data error detection: Data error detection is the process where the system automatically detects and corrects errors in PQ monitoring data. In Reference [143][105], an automatic detection and correction of errors system was developed based on data captured by PQ meters installed on a UK smart grid. The objective of the automatic system was to reduce the number of errors caused by various factors, such as poor installation of the devices, poor synchronization between multiple PQMs or by non-captured data (missing data), and maximizing the useful data for future network operations. The authors conclude that the number of errors can be reduced considerably by adopting a correct installation procedure for PQ monitoring devices.

Load Modeling: To represent the loads of an electrical network, mathematical models are used to simulate the dynamic or static behavior considering the active and reactive power of the load with respect to the variation of the voltage and frequency. In Reference [144][106], the authors derived the parameters of a dynamic load model of an 11 kV distribution network using a power quality monitoring system. The measurements used in the load model includes voltages, currents, active power, and reactive power at a sampling frequency of 1.6 kHz. To validate these results, the distribution network was simulated in a software using the parameters of the load model obtained and the load response to a disturbance was compared against a real disturbance in the distribution system captured by the PQMs. The general conclusion of this work was that 30–40% of the commercial loads considered in the distribution network are composed of induction motor loads, and if you want to make an accurate load model at the distribution level it is imperative to consider them.

3. Conclusions

This work made a comparison of eight advanced measurement devices for distribution networks based on their technical characteristics, including the sample frequency, reporting periods, measuring data, costs, precision, and time response. The comparative results showed that micro-phasor measurement unit and power quality monitor devices have the best performance overall to track dynamic and transitory events in distribution systems, due to their high-precision measurements, communication systems and remote storage of the extracted data.

This work also reviewed the most recent applications of micro-PMU, smart meters, and PQM data, considering novel methods and techniques. In addition, an input-output table that relates measured quantities from micro-PMU and smart meters needed for each specific application was developed in this review. From the extended literature reviewed in this work, the following conclusions are drawn:

  • The dominant applications of interest for PMU data is currently leaning towards analyzing situational awareness events and estimating the state variables of the system in near real-time. With the extremely high resolution (sampling rate up to 30,720 s/s), amplitude accuracy of 0.05%, and angle accuracy of 0.01%, it is possible to visualize transitory events in the distribution network. The sensor accuracy can have a strong influence on the uncertainty of the quantities to be measured and thus can highly impacting in the algorithms performance.

  • The dominant application of interest of smart meter data is currently driven to forecast future load consumption in a short term horizon based on artificial intelligence, machine learning, and deep learning techniques. Topology identification is also of current interest due to the limited knowledge about the topology of low voltage networks. Some novel methods are related to correlation techniques and graph theory methods.

  • The most recent applications of PQM devices are related to find the optimal placement of the PQM based on multiple objectives, focusing on minimizing the cost of monitoring, minimizing topological ambiguity and maximizing the load monitoring.

The integration of micro-PMU, PQM, and smart meters is an alternative to improve visibility, precision, and security in active distribution systems. However, the large amount of data generated with the use of these devices is a challenge that demands high computational complexity and the development of efficient algorithms with the ability to process information in real-time. Data connectivity with different resolutions, parameters, and locations is a challenge that requires further investigation.

 

References

  1. Fang, X.; Misra, S.; Xue, G.; Yang, D. Smart grid—The new and improved power grid: A survey. IEEE Commun. Surv. Tutor. 2011, 14, 944–980.
  2. Walling, R.; Saint, R.; Dugan, R.C.; Burke, J.; Kojovic, L.A. Summary of distributed resources impact on power delivery systems. IEEE Trans. Power Deliv. 2008, 23, 1636–1644.
  3. Brown, R.E. Impact of smart grid on distribution system design. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–4.
  4. Dileep, G. A survey on smart grid technologies and applications. Renew. Energy 2020, 146, 2589–2625.
  5. Kabalci, Y. A survey on smart metering and smart grid communication. Renew. Sustain. Energy Rev. 2016, 57, 302–318.
  6. Morello, R.; Mukhopadhyay, S.C.; Liu, Z.; Slomovitz, D.; Samantaray, S.R. Advances on sensing technologies for smart cities and power grids: A review. IEEE Sens. J. 2017, 17, 7596–7610.
  7. Ali, S.; Jawad, M.; Khan, B.; Mehmood, C.; Zeb, N.; Tanoli, A.; Farid, U.; Glower, J.; Khan, S. Wide area smart grid architectural model and control: A survey. Renew. Sustain. Energy Rev. 2016, 64, 311–328.
  8. Von Meier, A.; Culler, D.; McEachern, A.; Arghandeh, R. Micro-synchrophasors for distribution systems. In Proceedings of the ISGT 2014, Istanbul, Turkey, 12–15 October 2014; pp. 1–5.
  9. Von Meier, A.; Stewart, E.; McEachern, A.; Andersen, M.; Mehrmanesh, L. Precision micro-synchrophasors for distribution systems: A summary of applications. IEEE Trans. Smart Grid 2017, 8, 2926–2936.
  10. Arghandeh, R. Micro-Synchrophasors for Power Distribution Monitoring, a Technology Review. arXiv 2016, arXiv:1605.02813.
  11. Mohsenian-Rad, H.; Stewart, E.; Cortez, E. Distribution synchrophasors: Pairing big data with analytics to create actionable information. IEEE Power Energy Mag. 2018, 16, 26–34.
  12. Dusabimana, E.; Yoon, S.G. A Survey on the Micro-Phasor Measurement Unit in Distribution Networks. Electronics 2020, 9, 305.
  13. Liu, Y.; Wu, L.; Li, J. D-PMU based applications for emerging active distribution systems: A review. Electr. Power Syst. Res. 2020, 179, 106063.
  14. Wang, Y.; Chen, Q.; Hong, T.; Kang, C. Review of smart meter data analytics: Applications, methodologies, and challenges. IEEE Trans. Smart Grid 2018, 10, 3125–3148.
  15. Yildiz, B.; Bilbao, J.I.; Dore, J.; Sproul, A.B. Recent advances in the analysis of residential electricity consumption and applications of smart meter data. Appl. Energy 2017, 208, 402–427.
  16. McKenna, E.; Richardson, I.; Thomson, M. Smart meter data: Balancing consumer privacy concerns with legitimate applications. Energy Policy 2012, 41, 807–814.
  17. Alahakoon, D.; Yu, X. Smart electricity meter data intelligence for future energy systems: A survey. IEEE Trans. Ind. Inf. 2015, 12, 425–436.
  18. Haitao, Y.; Tao, R.; Junyi, C.; Yun, Z.; Junjie, C.; Jiachao, H.; Guofa, Z.; Bo, M. Usage and Application of Power Quality Monitor on Harmonic Measurement. In Proceedings of the 2018 IEEE 3rd International Conference on Integrated Circuits and Microsystems (ICICM), Shanghai, China, 24–26 November 2018; pp. 212–216.
  19. Kamyabi, L.; Esmaeili, S.; Koochi, M.H.R. Power quality monitor placement in power systems considering channel limits and estimation error at unobservable buses using a bi-level approach. Int. J. Electr. Power Energy Syst. 2018, 102, 302–311.
  20. Dehghanpour, K.; Wang, Z.; Wang, J.; Yuan, Y.; Bu, F. A survey on state estimation techniques and challenges in smart distribution systems. IEEE Trans. Smart Grid 2018, 10, 2312–2322.
  21. Hyndman, R.J.; Liu, X.A.; Pinson, P. Visualizing big energy data: Solutions for this crucial component of data analysis. IEEE Power Energy Mag. 2018, 16, 18–25.
  22. Tu, C.; He, X.; Shuai, Z.; Jiang, F. Big data issues in smart grid–A review. Renew. Sustain. Energy Rev. 2017, 79, 1099–1107.
  23. Stewart, E.M.; Kiliccote, S.; Shand, C.; McMorran, A.; Arghandeh, R.; von Meier, A. Addressing the challenges for integrating micro-synchrophasor data with operational system applications. In Proceedings of the 2014 IEEE PES General Meeting| Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5.
  24. Kumar, P.; Lin, Y.; Bai, G.; Paverd, A.; Dong, J.S.; Martin, A. Smart grid metering networks: A survey on security, privacy and open research issues. IEEE Commun. Surv. Tutor. 2019, 21, 2886–2927.
  25. Duan, N.; Stewart, E.M. Frequency Event Categorization in Power Distribution Systems using Micro PMU Measurements. IEEE Trans. Smart Grid. 2020, 11, 3043–3053.
  26. Shahsavari, A.; Farajollahi, M.; Stewart, E.M.; Cortez, E.; Mohsenian-Rad, H. Situational awareness in distribution grid using micro-PMU data: A machine learning approach. IEEE Trans. Smart Grid. 2019, 10, 6167–6177.
  27. Cui, M.; Wang, J.; Florita, A.R.; Zhang, Y. Generalized Graph Laplacian Based Anomaly Detection for Spatiotemporal MicroPMU Data. IEEE Trans. Power Syst. 2019, 34, 3960–3963.
  28. Ardakanian, O.; Wong, V.W.; Dobbe, R.; Low, S.H.; von Meier, A.; Tomlin, C.J.; Yuan, Y. On identification of distribution grids. IEEE Trans. Control Netw. Syst. 2019, 6, 950–960.
  29. Farajollahi, M.; Shahsavari, A.; Stewart, E.M.; Mohsenian-Rad, H. Locating the source of events in power distribution systems using micro-PMU data. IEEE Trans. Power Syst. 2018, 33, 6343–6354.
  30. Jamei, M.; Scaglione, A.; Roberts, C.; Stewart, E.; Peisert, S.; McParland, C.; McEachern, A. Anomaly Detection Using Optimally-Placed Micro-PMU Sensors in Distribution Grids. arXiv 2017, arXiv:1708.00118.
  31. Zanjani, M.G.M.; Mazlumi, K.; Kamwa, I. Application of μPMUs for adaptive protection of overcurrent relays in microgrids. IET Gener. Trans. Distrib. 2018, 12, 4061–4068.
  32. Pignati, M.; Zanni, L.; Romano, P.; Cherkaoui, R.; Paolone, M. Fault detection and faulted line identification in active distribution networks using synchrophasors-based real-time state estimation. IEEE Trans. Power Deliv. 2016, 32, 381–392.
  33. Shahsavari, A.; Farajollahi, M.; Stewart, E.; Roberts, C.; Mohsenian-Rad, H. A data-driven analysis of lightning-initiated contingencies at a distribution grid with a PV farm using micro-PMU data. In Proceedings of the 2017 North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017; pp. 1–6.
  34. Zhou, Y.; Arghandeh, R.; Konstantakopoulos, I.; Abdullah, S.; von Meier, A.; Spanos, C.J. Abnormal event detection with high resolution micro-PMU data. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–7.
  35. Mahmood, F.; Hooshyar, H.; Lavenius, J.; Bidadfar, A.; Lund, P.; Vanfretti, L. Real-time reduced steady-state model synthesis of active distribution networks using pmu measurements. IEEE Trans. Power Deliv. 2016, 32, 546–555.
  36. Li, J.; Liu, H.; Martin, K.E.; Li, J.; Bi, T.; Yang, Q. Electronic transformer performance evaluation and its impact on PMU. IET Gener. Trans. Distrib. 2019, 13, 5396–5403.
  37. Moffat, K.; Bariya, M.; Von Meier, A. Unsupervised Impedance and Topology Estimation of Distribution Networks—Limitations and Tools. IEEE Trans. Smart Grid. 2019, 11, 846–856.
  38. Cavraro, G.; Arghandeh, R. Power distribution network topology detection with time-series signature verification method. IEEE Trans. Power Syst. 2017, 33, 3500–3509.
  39. Cavraro, G.; Arghandeh, R.; Poolla, K.; Von Meier, A. Data-driven approach for distribution network topology detection. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5.
  40. Niazazari, I.; Livani, H. A PMU-data-driven disruptive event classification in distribution systems. Electr. Power Syst. Res. 2018, 157, 251–260.
  41. Niazazari, I.; Livani, H. Disruptive event classification using PMU data in distribution networks. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5.
  42. Lin, C.; Wu, W.; Guo, Y. Decentralized Robust State Estimation of Active Distribution Grids Incorporating Microgrids Based on PMU Measurements. IEEE Trans. Smart Grid. 2019, 11, 810–820.
  43. Tsitsimelis, A.; Antón-Haro, C. A regularized state estimation scheme for a robust monitoring of the distribution grid. Intl. J. Electr. Power Energy Syst. 2020, 117, 105621.
  44. Liu, Y.; Li, J.; Wu, L. State estimation of three-phase four-conductor distribution systems with real-time data from selective smart meters. IEEE Trans. Power Syst. 2019, 34, 2632–2643.
  45. Farajollahi, M.; Shahsavari, A.; Mohsenian-Rad, H. Tracking state estimation in distribution networks using distribution-level synchrophasor data. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–9 August 2018; pp. 1–5.
  46. Majidi, M.; Etezadi-Amoli, M.; Livani, H. Distribution system state estimation using compressive sensing. Intl. J. Electr. Power Energy Syst. 2017, 88, 175–186.
  47. Luiso, M.; Macii, D.; Tosato, P.; Brunelli, D.; Gallo, D.; Landi, C. A low-voltage measurement testbed for metrological characterization of algorithms for phasor measurement units. IEEE Trans. Ins. Meas. 2018, 67, 2420–2433.
  48. Su, H.; Wang, C.; Li, P.; Liu, Z.; Yu, L.; Wu, J. Optimal placement of phasor measurement unit in distribution networks considering the changes in topology. Appl. Energy 2019, 250, 313–322.
  49. Marchi, P.; Messina, F.; Vega, L.R.; Galarza, C.G. Online tracking of sub-transient generator model variables using dynamic phasor measurements. Electr. Power Syst. Res. 2020, 180, 106057.
  50. Shahsavari, A.; Sadeghi-Mobarakeh, A.; Stewart, E.M.; Cortez, E.; Alvarez, L.; Megala, F.; Mohsenian-Rad, H. Distribution grid reliability versus regulation market efficiency: An analysis based on micro-PMU data. IEEE Trans. Smart Grid. 2017, 8, 2916–2925.
  51. Shahsavari, A.; Farajollahi, M.; Stewart, E.; von Meier, A.; Alvarez, L.; Cortez, E.; Mohsenian-Rad, H. A data-driven analysis of capacitor bank operation at a distribution feeder using micro-PMU data. In Proceedings of the 2017 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 23–26 April 2017; pp. 1–5.
  52. Cavraro, G.; Arghandeh, R.; Poolla, K.; Von Meier, A. Data-driven approach for distribution network topology detection. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5.
  53. Ahmed, S.; Lee, Y.; Hyun, S.H.; Koo, I. Unsupervised Machine Learning-Based Detection of Covert Data Integrity Assault in Smart Grid Networks Utilizing Isolation Forest. IEEE Trans. Inf. Forens. Secur. 2019, 14, 2765–2777.
  54. Araya, D.B.; Grolinger, K.; ElYamany, H.F.; Capretz, M.A.; Bitsuamlak, G. An ensemble learning framework for anomaly detection in building energy consumption. Energy Build. 2017, 144, 191–206.
  55. Moghaddass, R.; Wang, J. A hierarchical framework for smart grid anomaly detection using large-scale smart meter data. IEEE Trans. Smart Grid. 2017, 9, 5820–5830.
  56. Liu, X.; Iftikhar, N.; Nielsen, P.S.; Heller, A. Online anomaly energy consumption detection using lambda architecture. In International Conference on Big Data Analytics and Knowledge Discovery; Springer: Cham, Switzerland, 2016; pp. 193–209.
  57. Wang, S.; Chen, H.; Wu, L.; Wang, J. A novel smart meter data compression method via stacked convolutional sparse auto-encoder. Intl. J. Electr. Power Energy Syst. 2020, 118, 105761.
  58. Huang, X.; Hu, T.; Ye, C.; Xu, G.; Wang, X.; Chen, L. Electric load data compression and classification based on deep stacked auto-encoders. Energies 2019, 12, 653.
  59. de Souza, J.C.S.; Assis, T.M.L.; Pal, B.C. Data compression in smart distribution systems via singular value decomposition. IEEE Trans. Smart Grid 2015, 8, 275–284.
  60. Wang, Y.; Chen, Q.; Kang, C.; Xia, Q.; Luo, M. Sparse and redundant representation-based smart meter data compression and pattern extraction. IEEE Trans. Power Syst. 2016, 32, 2142–2151.
  61. Montañez, C.A.C.; Hurst, W. A Machine Learning Approach for Detecting Unemployment Using the Smart Metering Infrastructure. IEEE Access. 2020, 8, 22525–22536.
  62. Razavi, R.; Gharipour, A.; Fleury, M.; Akpan, I.J. Occupancy detection of residential buildings using smart meter data: A large-scale study. Energy Build. 2019, 183, 195–208.
  63. Sun, G.; Cong, Y.; Hou, D.; Fan, H.; Xu, X.; Yu, H. Joint household characteristic prediction via smart meter data. IEEE Trans. Smart Grid 2017, 10, 1834–1844.
  64. Wang, Y.; Chen, Q.; Gan, D.; Yang, J.; Kirschen, D.S.; Kang, C. Deep learning-based socio-demographic information identification from smart meter data. IEEE Trans. Smart Grid. 2018, 10, 2593–2602.
  65. Khan, Z.A.; Jayaweera, D. Smart Meter Data Based Load Forecasting and Demand Side Management in Distribution Networks with Embedded PV Systems. IEEE Access. 2019, 8, 2631–2644.
  66. Feng, C.; Sun, M.; Zhang, J. Reinforced deterministic and probabilistic load forecasting via Q-learning dynamic model selection. IEEE Trans. Smart Grid. 2019, 11, 1377–1386.
  67. Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid. 2017, 10, 841–851.
  68. Oprea, S.V.; Bâra, A. Machine Learning Algorithms for Short-Term Load Forecast in Residential Buildings Using Smart Meters, Sensors and Big Data Solutions. IEEE Access. 2019, 7, 177874–177889.
  69. Wang, Y.; Chen, Q.; Sun, M.; Kang, C.; Xia, Q. An ensemble forecasting method for the aggregated load with subprofiles. IEEE Trans. Smart Grid. 2018, 9, 3906–3908.
  70. Buzau, M.M.; Tejedor-Aguilera, J.; Cruz-Romero, P.; Gómez-Expósito, A. Hybrid deep neural networks for detection of non-technical losses in electricity smart meters. IEEE Trans. Power Syst. 2019, 35, 1254–1263.
  71. Taieb, S.B.; Huser, R.; Hyndman, R.J.; Genton, M.G. Forecasting uncertainty in electricity smart meter data by boosting additive quantile regression. IEEE Trans. Smart Grid. 2016, 7, 2448–2455.
  72. Arora, S.; Taylor, J.W. Forecasting electricity smart meter data using conditional kernel density estimation. Omega 2016, 59, 47–59.
  73. Akinsipe, O.C.; Leskarac, D.; Stegen, S.; Moya, D.; Kaparaju, P. The Utilisation of Smart Meter Technology to Increase Energy Awareness for Residential Buildings in Queensland, Australia. In Sustainability in Energy and Buildings; Springer: Cham, Switzerland, 2020; pp. 1–10.
  74. Ullah, A.; Haydarov, K.; Ul Haq, I.; Muhammad, K.; Rho, S.; Lee, M.; Baik, S.W. Deep Learning Assisted Buildings Energy Consumption Profiling Using Smart Meter Data. Sensors 2020, 20, 873.
  75. Haben, S.; Singleton, C.; Grindrod, P. Analysis and Clustering of Residential Customers Energy Behavioral Demand Using Smart Meter Data. IEEE Trans. Smart Gri. 2016, 7, 136–144.
  76. Wang, W.; Yu, N.; Foggo, B.; Davis, J.; Li, J. Phase identification in electric power distribution systems by clustering of smart meter data. In Proceedings of the 2016 15th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016; pp. 259–265.
  77. Ismail, M.; Shaaban, M.F.; Naidu, M.; Serpedin, E. Deep Learning Detection of Electricity Theft Cyber-attacks in Renewable Distributed Generation. IEEE Trans. Smart Grid. 2020, 11, 3428–3437.
  78. Jindal, A.; Dua, A.; Kaur, K.; Singh, M.; Kumar, N.; Mishra, S. Decision tree and SVM-based data analytics for theft detection in smart grid. IEEE Trans. Ind. Inf. 2016, 12, 1005–1016.
  79. Júnior, L.A.P.; Ramos, C.C.O.; Rodrigues, D.; Pereira, D.R.; de Souza, A.N.; da Costa, K.A.P.; Papa, J.P. Unsupervised non-technical losses identification through optimum-path forest. Electr. Power Syst. Res. 2016, 140, 413–423.
  80. Zhou, W.; Ardakanian, O.; Zhang, H.T.; Yuan, Y. Bayesian Learning-Based Harmonic State Estimation in Distribution Systems With Smart Meter and DPMU Data. IEEE Trans. Smart Grid 2019, 11, 832–845.
  81. Ledva, G.S.; Mathieu, J.L. Separating Feeder Demand into Components Using Substation, Feeder, and Smart Meter Measurements. IEEE Trans. Smart Grid 2020, 11, 3280–3290.
  82. Jiang, Y. Data-Driven Fault Location of Electric Power Distribution Systems With Distributed Generation. IEEE Trans. Smart Grid. 2019, 11, 129–137.
  83. Jiang, W.; Chen, J.; Tang, H.; Cheng, S.; Hu, Q.; Cai, M.; Rahman, S. A Physical Probabilistic Network Model for Distribution Network Topology Recognition Using Smart Meter Data. IEEE Trans. Smart Grid. 2019, 10, 6965–6973.
  84. Mokhtar, M.; Robu, V.; Flynn, D.; Higgins, C.; Whyte, J.; Loughran, C.; Fulton, F. Automating the Verification of the Low Voltage Network Cables and Topologies. IEEE Trans. Smart Grid. 2019.
  85. Pappu, S.J.; Bhatt, N.; Pasumarthy, R.; Rajeswaran, A. Identifying topology of low voltage distribution networks based on smart meter data. IEEE Trans. Smart Grid 2017, 9, 5113–5122.
  86. Peppanen, J.; Grijalva, S.; Reno, M.J.; Broderick, R.J. Distribution system low-voltage circuit topology estimation using smart metering data. In Proceedings of the 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, CO, USA, 2–5 May 2016; pp. 1–5.
  87. Weng, Y.; Liao, Y.; Rajagopal, R. Distributed energy resources topology identification via graphical modeling. IEEE Trans. Power Syst. 2016, 32, 2682–2694.
  88. Luan, W.; Peng, J.; Maras, M.; Lo, J.; Harapnuk, B. Smart meter data analytics for distribution network connectivity verification. IEEE Trans. Smart Grid 2015, 6, 1964–1971.
  89. Yu, J.; Sun, Y.; Lu, J.; Zou, Q.; Xie, X.; Fu, B.; Liu, W.; Ye, L.; Chen, Y. Optimal Placement of Power Quality Monitors in Complex Distribution Network Based on Topological Degradation. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 58–61.
  90. Branco, H.; Oleskovicz, M.; Coury, D.V.; Delbem, A.C.B. Multiobjective optimization for power quality monitoring allocation considering voltage sags in distribution systems. Intl. J. Electr. Power Energy Syst. 2018, 97, 1–10.
  91. Sheibani, M.; Ketabi, A.; Nosratabadi, M. Optimal power quality meters placement with consideration of single line and meter loss contingencies. Intl. J. Ind. Electron. Control Optimiz. 2018, 1, 81–89.
  92. Ali, S.; Wu, K.; Weston, K.; Marinakis, D. A machine learning approach to meter placement for power quality estimation in smart grid. IEEE Trans. Smart Grid 2015, 7, 1552–1561.
  93. Nasiri, S.; Seifi, H. Robust probabilistic optimal voltage sag monitoring in presence of uncertainties. IET Gener. Trans. Distrib. 2016, 10, 4240–4248.
  94. Pau, M.; Pegoraro, P.A.; Monti, A.; Muscas, C.; Ponci, F.; Sulis, S. Impact of current and power measurements on distribution system state estimation uncertainty. IEEE Trans. Ins. Meas. 2018, 68, 3992–4002.
  95. Xiao, F.; Ai, Q. Data-driven multi-hidden markov model-based power quality disturbance prediction that incorporates weather conditions. IEEE Trans. Power Syst. 2018, 34, 402–412.
  96. Mora-Florez, J.; Barrera-Nunez, V.; Carrillo-Caicedo, G. Fault location in power distribution systems using a learning algorithm for multivariable data analysis. IEEE Trans. Power Deliv. 2007, 22, 1715–1721.
  97. Kim, J.; Baran, M.E.; Lampley, G.C. Estimation of fault location on distribution feeders using PQ monitoring data. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–4.
  98. Elphick, S.; Gosbell, V.; Smith, V.; Perera, S.; Ciufo, P.; Drury, G. Methods for harmonic analysis and reporting in future grid applications. IEEE Trans. Power Deliv. 2016, 32, 989–995.
  99. Gasch, E.; Domagk, M.; Meyer, J.; Abdelrahman, S.; Liao, H.; Milanović, J.V. Assessment of power quality performance in distribution networks part I-Measurement campaign and initial analysis. In Proceedings of the 2016 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; pp. 164–169.
  100. Abdelrahman, S.; Liao, H.; Milanović, J.V.; Gasch, E.; Domagk, M.; Meyer, J. Assessment of Power Quality performance in distribution networks part II-Performance Indices and ranking of network buses. In Proceedings of the 2016 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; pp. 431–436.
  101. Yildirim, O.; Eristi, B.; Eristi, H.; Unal, S.; Erol, Y.; Demir, Y. FPGA-based online power quality monitoring system for electrical distribution network. Measurement 2018, 121, 109–121.
  102. Elphick, S.; Ciufo, P.; Drury, G.; Smith, V.; Perera, S.; Gosbell, V. Large scale proactive power-quality monitoring: An example from Australia. IEEE Trans. Power Deliv. 2016, 32, 881–889.
  103. Luo, L.; Chen, S.; Yang, Y.; Yuan, S.; Luo, H.; Hu, Y. Design and application of power quality monitoring system for the smart substation based on IEC 61850. CIRED-Open Access Proc. J. 2017, 2017, 577–580.
  104. Artale, G.; Cataliotti, A.; Cosentino, V.; Di Cara, D.; Guaiana, S.; Panzavecchia, N.; Tinè, G. Real-Time Power Flow Monitoring and Control System for Microgrids Integration in Islanded Scenarios. IEEE Trans. Ind. Appl. 2019, 55, 7186–7197.
  105. Blair, S.M.; Booth, C.D.; Williamson, G.; Poralis, A.; Turnham, V. Automatically detecting and correcting errors in power quality monitoring data. IEEE Trans. Power Deliv. 2016, 32, 1005–1013.
  106. Rahim, A.A.; Hashim, M.F.; Siam, M.M. Dynamic load modelling based on power quality recorder data. In Proceedings of the 2013 IEEE 7th International Power Engineering and Optimization Conference (PEOCO), Langkawi Island, Malaysia, 3–4 June 2013; pp. 119–123.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/)
Video Production Service
Feedback