Oscillatory Properties of Noncanonical Neutral DDEs of Second-Order

Oscillatory Properties of Noncanonical Neutral DDEs of Second-Order: Comparison

Please note this is a comparison between Version 5 by Lindsay Dong and Version 4 by Lindsay Dong.

A DDE is a single-variable differential equation, usually called time, in which the derivative of the solution at a certain time is given in terms of the values of the solution at earlier times. Moreover, if the highest-order derivative of the solution appears both with and without delay, then the DDE is called of the neutral type. The neutral DDEs have many interesting applications in various branches of applied science, as these equations appear in the modeling of many technological phenomena. The problem of studying the oscillatory and nonoscillatory properties of DDEs has been a very active area of research in the past few decades.

delay differential equation
neutral
oscillation
noncanonical case

1. Introduction

Consider the 2nd-order delay differential equation (DDE) of the neutral type:

(1)

where

t \in [t_{0}, \infty)

and

v (t) : = u (t) + a_{1} (t) u (g_{0} (t))

. In this entry, we obtain new sufficient criteria for the oscillation of solutions of (1) under the following hypotheses:

(A1)

β \geq 1

is a ratio of odd integers;

(A2)

a_{i} \in C ([t_{0}, \infty), [0, \infty))

for

i = 0, 1, 2,

a_{0} (t) > 0

a_{1} \leq c_{0}

a constant (this constant plays an important role in the results), and

a_{2}

does not vanish identically on any half-line

[t_{*}, \infty)

with

t_{*} \in [t_{0}, \infty);

(A3)

g_{j} \in C ([t_{0}, \infty), R)

g_{j} (t) \leq t

g_{0' (t) \geq g_{0 * > 0,}}

g_{0} \circ g_{1} = g_{1} \circ g_{0}

and

{lim}_{t \to \infty g_{j} (t) = \infty}

for

j = 0, 1

By a proper solution of (1), we mean a

u \in C^{1} ([t_{0}, \infty))

with

a_{0} \cdot (v^{' () β}) \in C^{1} ([t_{0}, \infty))

and

sup {|u (t)| : t \geq t_{*}} > 0,

for

t_{*} \in [t_{0}, \infty),

and u satisfies (1) on

[t_{0}, \infty)

. A solution u of (1) is called nonoscillatory if it is eventually positive or eventually negative; otherwise, it is called oscillatory.

The oscillatory properties of solutions of second-order neutral DDE (1) in the noncanonical case, that is:

(

)

where

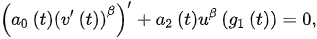
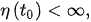
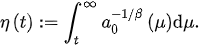
2. Oscillatory Properties of Noncanonical Neutral DDEs of Second-Order

We begin with the following notations: $U^{+}$ is the set of all eventually positive solutions of (1), $V (t) : = a_{0 1 / β (t) v^{'} (t)}$ ,

Lemma 1. Assume that $v \in U^{+}$ and there exists a $δ_{0} \in (0, 1)$ such that:

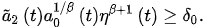
(3)

Then, v eventually satisfies:

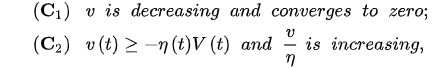
and:

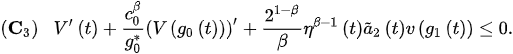
Proof. Let u ∈ U + . Then, we have that u g 0 t , and u g 1 t are positive for t ≥ t 1 , for some t 1 ≥ t 0 . Therefore, it follows from (1) that:

Using (1) and Lemma 1 in ^[1], we see that:

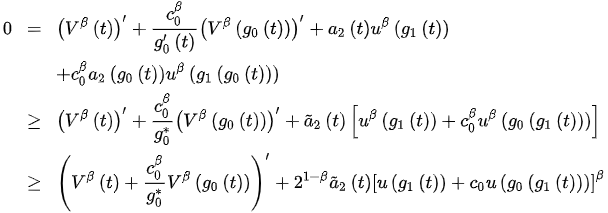
and so:

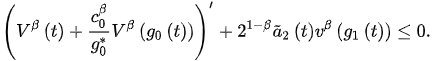
(4)

Integrating this inequality from t 1 to t and using the fact V β t ′ ≤ 0 , we find: ${(V^{β} (t))}^{'} \leq 0$

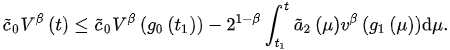
(5)

C 1 Assume the contrary, that v ′ t > 0 for t ≥ t 1 . Thus, from (5), we have:

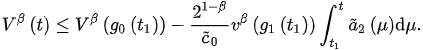
This, from (3), implies:

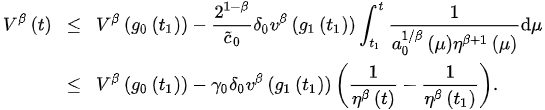
Letting t → ∞ and taking the fact that η t → 0 as t → ∞ , we obtain V β t → − ∞ $V^{β} (t) \to - \infty$ , which contradicts the positivity of V t . $V (t)$

References

Baculikova, B.; Dzurina, J. Oscillation theorems for second-order nonlinear neutral differential equations. Comput. Math. Appl. 2011, 62, 4472–4478.