Nano-(Q)SAR for Cytotoxicity Prediction of Engineered Nanomaterials

Nano-(Q)SAR for Cytotoxicity Prediction of Engineered Nanomaterials: Comparison

Please note this is a comparison between Version 2 by Peter Tang and Version 1 by Andrey Buglak.

engineered nanomaterials
safety of nanomaterials
toxicological tests
descriptors
QSAR
machine learning
modeling

1. Introduction

Nanomaterials and nanoparticles (NPs) possess unique physico-chemical properties (size, shape, chemical composition, physiochemical stability, crystal structure, surface area, surface energy, and surface roughness ^[1]), which give them beneficial characteristics. For this reason, nanotechnology is a new and rapidly growing field of knowledge which includes design, development, and usage of NPs and nanomaterials. According to the Organization for Economic Co-operation and Development (OECD), there exist 11 types of engineered nanomaterials (ENMs): Cerium oxide, dendrimers, fullerenes, gold nanoparticles, multi-walled carbon nanotubes (MWCNTs), nanoclays, silicon dioxide, silver nanoparticles, single-walled carbon nanotubes (SWCNTs), titanium dioxide, and zinc oxide.

The toxicity of ENMs and their influence on humans and the environment should be carefully evaluated [2,3]^[2][3]. Generally, there are five key mechanisms of ENMs’ toxicity: (1) Direct lesion by ion detachment; (2) oxidative stress induced by reactive oxygen species; (3) adsorption of biologically active molecules; (4) photochemical and redox reactions; and (5) Trojan horse effects (NPs may act as vectors for the transport of toxic compounds into cells) [4,5,6,7,8]^{[4][5][6][7][8]}. Not only is complete experimental characterization of the toxicity for all varying preparations extremely laborious, but predictions of the theoretical descriptions of the correspondence between structure/composition of ENMs and their biological activity are in demand.

Quantitative structure-activity relationship, or QSAR (Figure 1), is an area of molecular modeling that studies relationships between structure and activity using mathematical statistics and machine learning methods. QSAR is efficiently used to predict toxicity of chemical substances [9,10,11,12,13]^{[9][10][11][12][13]}. Classical QSAR is a so-called Hansch analysis ^[14], which stands on the assumption that bioactivity of compounds is correlated with geometrical and physicochemical descriptors. Generally, a molecular descriptor can be considered as a “number” describing a certain molecular property, which might be experimentally determined (i.e., dipole moment) or calculated (i.e., potential energy), or determined from the chemical structure (i.e., number of methyl groups). However, a molecular descriptor may be a mathematically obtained property (i.e., Wiener, Balaban, or Randic indices)—chemical graph theory is often used to derive mathematical descriptors ^[15]. Three-dimensional QSAR is another approach which allows building relations between the spatial structure of molecules, interaction fields, and activity. The first application of the three-dimensional (3D) QSAR technique was proposed in 1988 by Cramer and co-authors ^[16], when they were first to develop comparative molecular field analysis (CoMFA). CoMFA supposes that differences in bio-activity depend on the change of strength of non-covalent interaction fields (electrostatic and van der Waals) around the molecules. Another 3D QSAR method is comparative molecular similarity indices analysis (CoMSIA), which takes into account the same molecular interactions as CoMFA, but with the addition of hydrophobic interactions and hydrogen bonding. CoMSIA was developed in 1994 ^[17]. Three-dimensional QSAR provides multiple benefits to a researcher who studies organic compounds. However, 3D QSAR and classical molecular descriptors are unable to express the specificity of nanoparticles, because their exact structure is usually unknown. This circumstance leads to a lack of sufficient molecular descriptors appropriate for nano-QSAR modeling ^[18].

/media/item_content/202112/61bfdc20472fdmolecules-24-04537-g001.png

Figure 1.

A typical workflow of QSAR modeling for nanoparticles (NPs).

Nano-QSAR (Figure 2) allows the efficient study of nanoparticles and determination of correlations between their structure and activity ^[19]. Nano-QSAR may use all three approaches: One-dimensional (1D), two-dimensional (2D), and 3D QSAR [20,21,22]^[20][21][22]. However, it also raises a question: Which technique (nano-Hansch, nano-CoMFA, or nano-CoMSIA) is the best way to study nano-objects? There have been attempts to answer this question. Jagiello and co-authors compared the performance of nano-QSAR and 3D nano-QSAR, studying the activity of fullerene derivatives ^[23]. They concluded that nano-QSAR is a more universal approach, which allows gathering general information about the mode of biological activity of nanomaterials: Not only the receptor-based response, but also cell- and organism-based responses. The latter allows efficiently predicting the toxicity of nanoparticles. However, the application of 3D QSAR should be used to study the receptor-based response and would help in understanding such activity in detail ^[23]. In general, application of QSAR modeling of nanomaterials can reduce the need for time- and labor-consuming cytotoxicity tests, which are extremely important and economically feasible.

/media/item_content/202112/61bfdc3edd760molecules-24-04537-g002.png

Figure 2. A general scheme of nano-(Q)SAR modeling. 0D, zero-dimensional; 1D, one-dimensional; 2D, two-dimensional; 3D, three-dimensional.

2. Metal Oxides

Metal oxide NPs are used in renewable energy, wastewater treatment, electronics, cosmetics, textiles, foods, agriculture, medicine, pharmaceutics, and for many other purposes. Metal oxides are probably the most well-studied object of nano-QSAR research. The pioneer work by Hu et al. investigated seven nano-sized metal oxides: ZnO, CuO, Al₂O₃, La₂O₃, Fe₂O₃, SnO₂, and TiO₂. They applied the multiple linear regression (MLR) method. The cytotoxicity towards Escherichia coli was found to be highly correlated with metal cation charge. The higher the cation charge, the lower the cytotoxicity of the nano-sized metal oxide [25]^[24]. The cytotoxicity of metal oxide ENMs were measured in terms of LD₅₀: The dosage of NPs shown to cause the death of 50% of E. coli cells.

The oxidative stress potential of metal oxide NPs could be predicted by looking at their band gap energy ^[5]. Puzyn and co-authors developed a model describing the cytotoxicity towards Escherichia coli of nanoparticles based on 16 different metal oxides and SiO₂ ^[20]. All quantum-chemical calculations were performed using the PM6 semi-empirical method. They applied the MLR method combined with a genetic algorithm. The model obtained was characterized by R² = 0.862. The model reliably predicted the toxicity of all metal oxides and included only one descriptor—ΔH_Me+—which is the enthalpy of formation of a gaseous cation. The endpoint of cytotoxicity measurement was LD₅₀. Log(1/LD₅₀) was used as a dependent variable in the MLR equation.

The structure–cytotoxicity relationship for the same dataset of 17 metal oxide NPs was further investigated in a succession of papers [18,26,27,28,29,30,31,32]^{[18][25][26][27][28][29][30][31]}. Density functional theory (DFT)-based descriptors (energy gap, hardness, softness, electronegativity, and electrophilicity index), in conjunction with the MLR statistical method, were used to find a high correlation between experimental and predicted activity values [27]^[26]. The absolute electronegativity is defined as half of the summation between the ionization potential and the electron affinity. The absolute hardness is defined as half the difference between the ionization potential and the electron affinity. Within the Koopmans’ theorem approximation, these parameters can be expressed as the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energies. Thus, electronegativity (χ) is determined according to the equation:

Hardness (η) is determined according to the equation:

In a model by Kar et al., electronegativity (χ) and charge of the metal cation were used as molecular descriptors to build QSAR models for the prediction of cytotoxicity of metal oxide NPs (Table 1). They hypothesized that small particles of metal oxides release an electron much easier than the same particles in the crystal structure; small fragments initiate formation of reactive oxygen species, which invoke the oxidative stress condition to bacteria [28]^[27]. A simple QSAR model with high predictive ability (R² = 0.87) was built based on two descriptors: Absolute electronegativity of metal and electronegativity of metal oxide [32]^[31]. In addition, a high correlation (R² = 0.804) was obtained to predict the photo-toxicity of metal oxide NPs using two descriptors: Molar heat capacity and LUMO energy of the metal oxide [32]^[31]. The best model by Mu et al. associated cytotoxicity of 16 metal oxide NPs towards E. coli with enthalpy of formation of a gaseous cation (ΔH_me+) and polarization force (Z/r) [33]^[32]:

Log(1/EC₅₀) = (4.412 ± 0.165) + (−0.121 ± 0.068) Z/r + (0.001 ± 2.57 × 10⁻⁴)ΔH_me+

The model by Pan et al. used the same dataset, a simplified molecular input line entry system (SMILES)-based optimal descriptor and the MLR method, and showed the highest predictive ability towards both training (R² = 0.89–0.98) and test set (R² (test) = 0.82–0.87) ^[18]. Other works [20,27,28,32,33]^{[20][26][27][31][32]} also used the MLR method.

Table 1. Main features of (Q)SAR models predicting cytotoxicity of metal oxide nanoparticles.

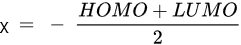
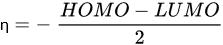
Source	Dataset	Endpoint of Cytotoxicity Measurement	n

Source

Dataset

Cell Type

^{2 1}

Source

Endpoint of Cytotoxicity Measurement

Dataset

Software

Statistical Method

Descriptors

Source

Dataset

Cell Type

Endpoint of Cytotoxicity Measurement

R²

Software

Software ²

R²

Statistical Method

Descriptors

Software

Statistical Method

Descriptors

Statistical Method

Descriptors

Escherichia coli

[59]^[55]

[74

[60]^[56]

Monocytes, hepatocytes, endothelial, and smooth muscle cells

Cellular viability

0.72

WinSVM, ISIDA

]^[69]

[

[78]^[73]

[83]^[78]

75]^[70]

[77,79]^[72][74]

[84]^[79]

Salmonella typhimurium TA100

Reverse mutation test TA100

Human embryonic kidney cells HEK293

Cell viability (%)

0.65–0.81

0.60–0.78

CORAL

SVM classification and k Nearest Neighbors (kNN) regression

Monte Carlo

0.80–0.93

CORAL

Monte Carlo

Size, zeta potential, R1 and R2 relaxivities

Quasi-SMILES

Monte Carlo

Quasi-SMILES

[25]^[24]

[59]^[55]

[25]^[24]

[[61]^[57]

LD₅₀

PaCa2 human pancreatic cancer cells, U937 macrophage cell lines, primary human macrophages, HUVEC human umbilical vein endothelial cells

]^[71

0.979

[77]^[72]

Salmonella typhimurium TA100

Multiple linear regression (MLR)

Metal cation charge

Reverse mutation test TA100

0.53–0.64

CORAL

Monte Carlo

Quasi-SMILES

[81]^[76]

[79]^[74]

S. typhimurium TA100

Cellular uptake

Reverse mutation test TA100

109

0.65–0.80

0.76

CORAL

Monte Carlo

[24]^[80]

[85]^[81]

WinSVM, ISIDA

Quasi-SMILES

Human kidney cells HK-2

Cell viability (%)

SVM classification and k Nearest Neighbors (kNN) regression

0.83–0.89

CORAL

Monte Carlo

Lipophilicity, number of double bonds

Quasi-SMILES

^[20]

[62]^[58]

[78]^[73]

[82]^[77]

^20]

[60

[77,79]

LD₅₀

]^[72

0.862

^56]^[

MATLAB

[86]^[82]

^]^74]

[79]^[74]

[86]^[82

Salmonella typhimurium TA100

S. typhimurium TA100

Reverse mutation test TA100

16HBE, A549, HaCaT, NRK-52E, and

THP-1

MLR

Enthalpy of formation of a gaseous cation

Smooth muscle cells

Cell apoptosis

Reverse mutation test TA100

0.81

EC₂₅

0.60–0.78

CORAL

MLR and Bayesian regularized artificial neural network

Monte Carlo

I_Fe2O3

Quasi-SMILES

0.63–0.76

CORAL

Monte Carlo

, I_dextran

Quasi-SMILES

0.83

CORAL

, and I

_surf.chg

Monte Carlo

Quasi-SMILES

[26]^[25]

[63]^[59]

^[20]

[

[60]^[56]

LD₅₀

80]^[75

Monocytes, hepatocytes, endothelial, and smooth muscle cells

0.741–0.838

[82]^[77]

[80

[86]^[82]

]^[75]

[79]^[74]

CORAL

Monte Carlo

SMILES-based optimal descriptor

Four types of normal human lung cells (BEAS-2B, 16HBE14o-, WI-38, and HBE)

Cellular viability

Cell viability (%)

E. coli WP2 uvrA/pKM101

[86]^[82]

276

16HBE, A549, HaCaT, NRK-52E, and

Reverse mutation test WP2 uvrA/pKM101

0.60–0.80

CORAL

0.68–0.82

CORALNaive Bayesian classifier

Monte Carlo

Primary size, spin-lattice and spin-spin relaxivities, zeta potential

Quasi-SMILES

[27]^[26]

[64]^[60]

^[20]

6. Silica Nanomaterials

Silica (SiO₂), or silicon dioxide, is one of the most commonly used ENMs. Silica can be divided into two types: Non-crystalline (amorphous) and crystalline. Amorphous SiO₂ is also divided into natural amorphous silica and synthetic SiO₂. SiO₂ has been studied thoroughly, along with metal oxide NPs, which are discussed above. Here, we concentrate exclusively on silica NPs. Table 5 summarizes the information about nano-(Q)SAR models predicting cytotoxicity of silica nanomaterials.

Table 5. Main features of (Q)SAR models predicting cytotoxicity of silica nanomaterials.

THP-1

₂₅

0.87

Aspect ratio and zeta potential

[64]^[

[87]^[83]

^60]

[LD₅₀

84]^[79

0.933

Zebrafish embryo

Human embryonic

kidney cell line (HEK293)

Minitab 16

24 h post-fertilization mortality

Cell viability (%)

MLR

ABMiner

Energy gap, hardness, softness, electronegativity, and electrophilicity index

Numerical prediction

0.80–0.95

Concentration, shell composition, surface functional groups, purity, core structure, and surface charge

CORAL

Monte Carlo

Quasi-SMILES

[28]^[27]

[65]^[61]

^[20]

[65]^[61]

LD₅₀

0.81–0.90

Mammalian cell lines

MLR

STATISTICA v.6

Electronegativity, charge of the metal cation corresponding to a given oxide

₅₀

LDA

Molar volume, polarizability, and size of the particles

[29]^[28]

[66]^[62

^[20]

[66]^[62]

LD₅₀

Algae, bacteria, cell lines, crustaceans, plants, fish, and others

CC₅₀, EC₅₀, IC₅₀

0.93

, TC₅₀, LC₅₀

RandomForest package

Random forest (RF)

36488

STATISTICA

₁—unbonded two-atomic fragments [Me] … [Me], which were encoded based on Simplex representation of molecular structures (SiRMS)-derived descriptors [34,35]^[33][34], describing distance where potential reaches minimum at van der Waals interactions; rw—Wigner–Seitz radius; ρ—mass density; (CPP)—cation polarizing power; S₂—SiRMS-derived electronegativity aligned descriptor of oxides molecules—in a sense of the acid-base property of oxides (this parameter increases with a number of oxygens in molecule); S₃—tri-atomic fragments [Me]-[O]-[Me], which were encoded by SiRMS-derived descriptors, encoding electronegativity; and (SV)—proportion of surface molecules to molecules in volume

LDA

Molar volume, polarizability, size of NPs, electronegativity, hydrophobicity, and polar surface area of surface coating

[30]^[29]

^[20]

LD₅₀

0.955

Ensemble learning

Oxygen percent, molar refractivity, and polar surface area

[67]^[63]

Bacteria, algae, crustaceans, fish, and others

EC₅₀, IC₅₀, TC₅₀, LC₅₀

5520

STATISTICA

LDA

Molar volume, electronegativity, polarizability, and nanoparticle size

[31]^[30]

^[20]

LD₅₀

MATLAB

Read-across

Ionization enthalpy of the detached metal atoms

^[18]

^[20]

LD₅₀

[68]^[64]

Algae, bacteria, fungi, mammal cell lines,

crustaceans, plants, fishes, and others

CC₅₀, EC₅₀, IC₅₀, TC₅₀, LC₅₀

54371

STATISTICA

Artificial neural network

Polar surface area, hydrophobicity, atomic weight, atomic van der Waals radius, electronegativity, and polarizability

[69]^[

0.889–0.982

^65]

[70]^[66]

CORAL

Danio rerio, Daphnia magna, Pseudokirchneriella subcapitata, and Staphylococcus aureus

LC₅₀, EC₅₀, MIC (minimum inhibitory concentration)

MLR

SMILES-based optimal descriptor

400

Weka

Functional tree, C4.5 decision tree, random tree, and CART

Molecular polarizability, accessible surface area, and solubility

[36]^[35]

^[20]

LD₅₀

0.91

MLR

Enthalpy of formation of a gaseous cation (ΔH

[71]^[67]

E. coli and Chinese hamster ovary (CHO-K1) cells

EC₅₀, MIC

_Me+

), charge of the metal cation (χ

_ox), and pEC₅₀ of HaCaT

0.94

Nonlinear least-squaress

Size and specific surface area (Brunauer-Emmett-Teller surface)

[33]^[32]

^[20]

LD₅₀

0.879

SYBYL X1.1 and SPSS statistics v.17

MLR

Enthalpy of formation of a gaseous cation (ΔH_me+) and polarization force (Z/r)

[37]^[36]

^[20]

LD₅₀

0.79

CORAL

Monte Carlo

Quasi-SMILES

[38]^[37]

^[20]

LD₅₀

0.92

Counter propagation artificial neural network

Metal electronegativity by Pauling scale, number of metal atoms in oxide, number of oxygen atoms in oxide, and charge of metal cation

[39]^[38]

^[20]

LD₅₀

0.968

Oxygen in weight percentage and enthalpy of formation of a gaseous cation

[40]^[39]

^[20]

LD₅₀

0.877 and 0.903

MLR and support vector machines (SVM)

HOMO energy, α-LUMO and β-LUMO energy, the average of α-LUMO and β-LUMO, the energy gap between the frontier molecular orbitals ∆E, and molar heat capacity

^[8]

^[20]

LD₅₀

0.93

Partial least squares (PLS)

Charge of metal ion, metal ion charge-based SiRMS, number of oxygen atoms in brutto formula weighted by ionic potential, covalent index weighted by charge of metal ion, molecular weight of metal oxide weighed by size of nanoparticle, squared thickness of interfacial layer, van der Waals repulsion weighted by size of nanoparticle, and Wigner-Seitz radius weighted by size of nanoparticle

[32]^[31]

LD₅₀

0.87

Self-written program

MLR

Electronegativity of metal and electronegativity of metal oxide

[41]^[40]

IC₅₀

SVM

Conduction band energy and hydration enthalpy (ΔH_hyd)

Human keratinocyte cell line (HaCaT)

[29]^[28]

[42]^[41]

LD₅₀

0.96

RandomForest package

S₁, rw, ρ, (CI)—covalent index of the metal ion, S₂, and (AP)—aggregation parameter

[31]^[30]

[42]^[41]

LD₅₀

MATLAB

Read-across

Mulliken’s electronegativity

[42]^[41]

LD₅₀

0.93

MLR

Enthalpy of formation of metal oxide, Mulliken’s electronegativity

^[18]

[42]^[41]

LD₅₀

0.961–0.999

CORAL

MLR

SMILES-based optimal descriptor

[36]^[35]

[42]^[41]

LD₅₀

0.88

MLR

Enthalpy of formation of metal oxide (ΔH_f) nano-cluster, electronic chemical potential of the cluster, and pEC₅₀ of E. coli

[37]^[36]

[42]^[41]

LD₅₀

0.79

CORAL

Monte Carlo

Quasi-SMILES

[39]^[38]

[42]^[41]

LD₅₀

0.918

10-based logarithm of solubility measured in mol/L (LogS), topological polar surface area (TPSA), Mulliken’s electronegativity

^[8]

[42]^[41]

LD₅₀

0.83

PLS

Atom charge-based SiRMS descriptor, charge of the atom weighted by the bond ionicity, charge of metal ion weighted by ionicity of bond, squared ionic potential, ion change-based SiRMS descriptor, number of oxygen atoms in brutto formula per interfacial layer, mass density weighted by ionicity of bond, Wigner-Seitz radius weighted by ionicity of bond, and ionicity of bond based SiRMS

[43]^[42]

[42,44,45]^[41][43][44]

Cell viability (%)

CORAL

Hierarchical cluster analysis (HCA) and min–max normalization

Quasi-SMILES

Transformed bronchial epithelial cells (BEAS-2B)

[46]^[45]

% of membrane-damaged cells

Weka

Atomization energy of the metal oxide, period of the nanoparticle metal, nanoparticle primary size, and nanoparticle volume fraction

^[6]

Cell viability (%)

Regression tree

Metal solubility and energy of conduction

[47]^[46]

^[6]

Cell viability (%)

RandomForest package

Mass density, covalent index, cation polarizing power, Wigner–Seitz radius, surface area-to-volume ratio, aggregation parameter, and tri-atomic descriptor of atomic charges

[48]^[47]

LD₅₀

RapidMiner

SVM

Conduction band energy and ionic index of metal cation

[49]^[48]

[50]^[49]

% of membrane-damaged cells

0.68

CORAL

Monte Carlo

SMILES-based optimal descriptor, dose, and exposure time

[43]^[42]

[6,51,52]^[6][50][51]

Cell viability (%)

0.713–0.733

CORAL

HCA and min-max normalization

Quasi-SMILES

Murine myeloid cells (RAW 264.7)

^[6]

Cell viability (%)

Regression tree

1681

Metal solubility and energy of conduction

[47]^[46]

^[6]

Cell viability (%)

RandomForest package

Mass density, molecular weight, aligned electronegativity, covalent index, surface area, surface area-to-volume ratio, two-atomic descriptor of van der Waals interactions, tetra-atomic descriptor of atomic charges, and size in DMEM

[48]^[47]

LD₅₀

RapidMiner

SVM

Conduction band energy and ionic index of metal cation

[53]^[52]

Lactate dehydrogenase (LDH) release

PLS

Metal cation charge, hydration rate, radius of the metallic cation, and Pauling electronegativity

Rat L2 lung epithelial cells and rat lung alveolar macrophages

[54]^[53]

Membrane damage (units L⁻¹)

Multivariate linear regression and linear discriminant analysis (LDA)

Size, concentration, size in phosphate buffered saline, size in water, and zeta potential

[55]^[54]

[54]^[53]

Membrane damage (units L⁻¹)

MLR and simple classification

Size, concentration, size in phosphate buffered saline, and size in water

¹ Missing R² value means that an SAR model was built instead of QSAR. ² If software record is missing, then it was not mentioned in the original paper.

3. Other Metal-Containing Nanoparticles

In a pioneer work [59]^[55], an SVM classification model was developed using the experimental data of 44 different NPs from Shaw et al. [60]^[56]. The model used four experimentally determined descriptors: Size, zeta potential evaluating the intensity of charge on their surface, and R1 and R2 relaxivities estimating their magnetic properties. The authors concluded that QSAR is an appropriate methodology for predicting the cytotoxicity of novel nanomaterials, as well as for the design and manufacture of safer NPs. Fourches and co-authors also analyzed a dataset by Weissledder et al. [61]^[57], where cellular uptake was evaluated. They used both SVM classification and kNN regression to build predictive models. The most important descriptors were lipoplicity and a number of double bonds [59]^[55]. Yet another nano-QSAR study for the prediction of the cytotoxicity of metal-containing NPs was conducted in [62]^[58] using smooth muscle cells from Shaw et al. [60]^[56]. The model was built based on cytotoxicity data for 31 NPs using MLR and a Bayesian regularized artificial neural network. The model predicting smooth muscle apoptosis (SMA) consisted of three descriptors: Core material (I_Fe2O3), surface coating (I_dextran), and surface charge (I_surf.chg):

SMA = 2.26(±0.72) − 10.73(±1.05)I_Fe2O3 – 5.57(±0.98)I_dextran – 3.53(±0.54)I_surf.chg

I_Fe2O3 was set to 1 for the Fe₂O₃ core and 0 when the core was Fe₃O₄. I_dextran was equal to 1 in the case of dextran coating and 0 for the others. Surface functionality was equal to 1 (basic), −1 (acidic), or 0 (neutral). The model possessed a determination coefficient for the training set equal to 0.81 and 0.86 for the test set. Table 2 summarizes the information about nano-(Q)SAR models predicting cytotoxicity of metal-containing nanoparticles.

Table 2. Main features of (Q)SAR models predicting cytotoxicity of metal-containing nanoparticles.

4. Multi-Walled Carbon Nanotubes (MWCNTs)

Certain MWCNTs display asbestos-like toxic effects. To reduce the need for risk assessment, it has been suggested that the physicochemical characteristics or reactivity of nanomaterials could be used to predict their hazard. Fiber-shape and ability to generate reactive oxygen species (ROS) are important indicators of high hazard materials. Asbestos is a known ROS generator, while MWCNTs may either produce or scavenge ROS [73]^[68]. Table 3 summarizes the information about nano-(Q)SAR models predicting cytotoxicity of MWCNTs.

Table 3. Main features of (Q)SAR models predicting cytotoxicity of multi-walled carbon nanotubes.

5. Fullerenes

Toropov et al. continued to study the toxicity of fullerenes in further publications. The experimental data on the cytotoxicity of C60 NPs towards Salmonella typhimurium was examined [79]^[74]. By means of quasi-SMILES descriptors obtained with the Monte Carlo method a mathematical model was constructed. The model was a function of dose, metabolic activation (S9 mix), and illumination (darkness or irradiation). Only one split into the training, calibration, and validation set was made. The statistical parameters of the model were not notably high: R² = 0.755, q² = 0.571 [81]^[76]. In the next study, two datasets were used for the bacterial reverse mutation test performed using either S. typhimurium or E. coli strain WP2 uvrA/pKM101 [79]^[74]. By means of the quasi-SMILES optimal descriptors calculated with the Monte Carlo method, mathematical models were built (several splits into the training, calibration, and validation set were made). The models were a function of the same experimental conditions as in the previous study: dose, metabolic activation, and illumination [82]^[77]. Table 4 summarizes the information about nano-(Q)SAR models predicting cytotoxicity of fullerenes.

Table 4. Main features of (Q)SAR models predicting cytotoxicity of fullerenes.

Source	Dataset	Cell Type	Endpoint of Cytotoxicity Measurement	n	R²

References

Gatoo, M.A.; Naseem, S.; Arfat, M.Y.; Dar, A.M.; Qasim, K.; Zubair, S. Physicochemical properties of nanomaterials: Implication in associated toxic manifestations. Biomed Res. Int. 2014, 2014, 498420.
Buzea, C.; Pacheco, I.I.; Robbie, K. Nanomaterials and nanoparticles: Sources and toxicity. Biointerphases 2007, 2, 17–71.
Gajewicz, A.; Rasulev, B.; Dinadayalane, T.C.; Urbaszek, P.; Puzyn, T.; Leszczynska, D.; Leszczynski, J. Advancing risk assessment of engineered nanomaterials: Application of computational approaches. Adv. Drug Deliv. Rev. 2012, 64, 1663–1693.
Valko, M.; Morris, H.; Cronin, M.T. Metals, toxicity and oxidative stress. Curr. Med. Chem. 2005, 12, 1161–1208.
Burello, E.; Worth, A.P. A theoretical framework for predicting the oxidative stress potential of oxide nanoparticles. Nanotoxicology 2011, 5, 228–235.
Zhang, H.; Ji, Z.; Xia, T.; Meng, H.; Low-Kam, C.; Liu, R.; Pokhrel, S.; Lin, S.; Wang, X.; Liao, Y.P.; et al. Use of metal oxide nanoparticle band gap to develop a predictive paradigm for oxidative stress and acute pulmonary inflammation. ACS Nano 2012, 6, 4349–4368.
Lynch, I.; Weiss, C.; Valsami-Jones, E. A strategy for grouping of nanomaterials based on key physico-chemical descriptors as a basis for safer-by-design NMs. Nano Today 2014, 9, 266–270.
Kuz’min, V.E.; Ognichenko, L.N.; Sizochenko, N.; Chapkin, V.A.; Stelmakh, S.I.; Shyrykalova, A.O.; Leszczynski, J. Combining features of metal oxide nanoparticles: Nano-QSAR for cytotoxicity. Int. J. Quant. Struct. Prop. Relat. 2019, 4, 28–40.
Tang, W.; Chen, J.; Wang, Z.; Xie, H.; Hong, H. Deep learning for predicting toxicity of chemicals: A mini review. J. Environ. Sci. Health C Environ. Carcinog. Ecotoxicol. Rev. 2018, 36, 252–271.
Idakwo, G.; Luttrell, J.; Chen, M.; Hong, H.; Zhou, Z.; Gong, P.; Zhang, C. A review on machine learning methods for in silico toxicity prediction. J. Environ. Sci. Health C Environ. Carcinog. Ecotoxicol. Rev. 2018, 36, 169–191.
Zhang, L.; Zhang, H.; Ai, H.; Hu, H.; Li, S.; Zhao, J.; Liu, H. Applications of Machine Learning Methods in Drug Toxicity Prediction. Curr. Top. Med. Chem. 2018, 18, 987–997.
Lu, J.; Lu, D.; Fu, Z.; Zheng, M.; Luo, X. Machine learning-based modeling of drug toxicity. Methods Mol. Biol. 2018, 1754, 247–264.
Kar, S.; Leszczynski, J. Exploration of computational approaches to predict the toxicity of chemical mixtures. Toxics 2019, 7, 15.
Hansch, C.; Streich, M.; Geiger, F.; Muir, R.M.; Maloney, P.P.; Fujita, T. Correlation of biological activity of plant growth regulators and chloromycetin derivatives with Hammett constants and partition coefficients. J. Am. Chem. Soc. 1963, 85, 2817–2824.
Bonchev, D.; Rouvray, D.H. Chemical Graph Theory: Introduction and Fundamentals; Taylor & Francis: London, UK, 1991.
Cramer, R.D.; Patterson, D.E.; Bunce, J.D. Comparative molecular field analysis (CoMFA). 1. Effect of shape on binding of steroids to carrier proteins. J. Am. Chem. Soc. 1988, 110, 5959–5967.
Klebe, G.; Abraham, U.; Mietzner, T. Molecular similarity indexes in a comparative-analysis (Comsia) of drug molecules to correlate and predict their biological-activity. J. Med. Chem. 1994, 37, 4130–4146.
Pan, Y.; Li, T.; Cheng, J.; Telesca, D.; Zink, J.I.; Jianga, J. Nano-QSAR modeling for predicting the cytotoxicity of metal oxide nanoparticles using novel descriptors. RSC Adv. 2016, 6, 25766–25775.
Burello, E.; Worth, A.P. QSAR modeling of nanomaterials. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2011, 3, 298–306.
Puzyn, T.; Rasulev, B.; Gajewicz, A.; Hu, X.; Dasari, T.P.; Michalkova, A.; Hwang, H.M.; Toropov, A.; Leszczynska, D.; Leszczynski, J. Using nano-QSAR to predict the cytotoxicity of metal oxide nanoparticles. Nat. Nanotechnol. 2011, 6, 175–178.
Tzoupis, H.; Leonis, G.; Durdagi, S.; Mouchlis, V.; Mavromoustakos, T.; Papadopoulos, M.G. Binding of novel fullerene inhibitors to HIV-1 protease: Insight through molecular dynamics and molecular mechanics Poisson-Boltzmann surface area calculations. J. Comput. Aided Mol. Des. 2011, 25, 959–976.
Ahmed, L.; Rasulev, B.; Turabekova, M.; Leszczynska, D.; Leszczynski, J. Receptor- and ligand-based study of fullerene analogues: Comprehensive computational approach including quantum-chemical, QSAR and molecular docking simulations. Org. Biomol. Chem. 2013, 11, 5798–5808.
Jagiello, K.; Grzonkowska, M.; Swirog, M.; Ahmed, L.; Rasulev, B.; Avramopoulos, A.; Papadopoulos, M.G.; Leszczynski, J.; Puzyn, T. Advantages and limitations of classic and 3D QSAR approaches in nano-QSAR studies based on biological activity of fullerene derivatives. J. Nanopart. Res. 2016, 18, 256.
Hu, X.; Cook, S.; Wang, P.; Hwang, H.M. In vitro evaluation of cytotoxicity of engineered metal oxide nanoparticles. Sci. Total Environ. 2009, 407, 3070–3072.
Toropov, A.A.; Toropova, A.P.; Benfenati, E.; Gini, G.; Puzyn, T.; Leszczynska, D.; Leszczynski, J. Novel application of the CORAL software to model cytotoxicity of metal oxide nanoparticles to bacteria Escherichia coli. Chemosphere 2012, 89, 1098–1102.
Venigalla, S.; Dhail, D.; Ranjan, P.; Jain, S.; Chakraborty, T. Computational study about cytotoxicity of metal oxide nanoparticles invoking nano-QSAR. New Front. Chem. 2013, 23, 123–130.
Kar, S.; Gajewicz, A.; Puzyn, T.; Roy, K.; Leszczynski, J. Periodic table-based descriptors to encode cytotoxicity profile of metal oxide nanoparticles: A mechanistic QSTR approach. Ecotox. Environ. Safe. 2014, 107, 162–169.
Sizochenko, N.; Rasulev, B.; Gajewicz, A.; Kuz’min, V.; Puzyn, T.; Leszczynski, J. From basic physics to mechanisms of toxicity: The “liquid drop” approach applied to develop predictive classification models for toxicity of metal oxide nanoparticles. Nanoscale 2014, 6, 13986–13993.
Singh, K.P.; Gupta, S. Nano-QSAR modeling for predicting biological activity of diverse nanomaterials. RSC Adv. 2014, 4, 13215–13230.
Gajewicz, A.; Cronin, M.; Rasulev, B.; Leszczynski, J.; Puzyn, T. Novel approach for efficient predictions properties of large pool of nanomaterials based on limited set of species: Nano-read-across. Nanotechnology 2015, 26, 015701.
Pathakoti, K.; Huang, M.-J.; Watts, J.D.; He, X.; Hwang, H.-M. Using experimental data of Escherichia coli to develop a QSAR model for predicting the photo-induced cytotoxicity of metal oxide nanoparticles. J. Photochem. Photobiol. B 2014, 130, 234–240.
Mu, Y.; Wu, F.; Zhao, Q.; Ji, R.; Qie, Y.; Zhou, Y.; Hu, Y.; Pang, C.; Hristozov, D.; Giesy, J.P.; et al. Predicting toxic potencies of metal oxide nanoparticles by means of nano-QSARs. Nanotoxicology 2016, 10, 1207–1214.
Kuz’min, V.E.; Artemenko, A.G.; Polischuk, P.G.; Muratov, E.N.; Hromov, A.I.; Liahovskiy, A.V.; Andronati, S.A.; Makan, S.Y. Hierarchic system of QSAR models (1D–4D) on the base of simplex representation of molecular structure. J. Mol. Model. 2005, 11, 457–467.
Kuz’min, V.E.; Muratov, E.N.; Artemenko, A.G.; Gorb, L.G.; Qasim, M.; Leszczynski, J. The effect of nitroaromatics composition on their toxicity in vivo. 1D QSAR research. Chemosphere 2008, 72, 1373–1380.
Kar, S.; Gajewicz, A.; Roy, K.; Leszczynski, J.; Puzyn, T. Extrapolating between toxicity endpoints of metal oxide nanoparticles: Predicting toxicity to Escherichia coli and human keratinocyte cell line (HaCaT) with Nano-QTTR. Ecotox. Environ. Safe. 2016, 126, 238–244.
Toropova, A.P.; Toropov, A.A.; Manganelli, S.; Leone, C.; Baderna, D.; Benfenati, E.; Fanelli, R. Quasi-SMILES as a tool to utilize eclectic data for predicting the behavior of nanomaterials. NanoImpact 2016, 1, 60–64.
Fjodorova, N.; Novic, M.; Gajewicz, A.; Rasulev, B. The way to cover prediction for cytotoxicity for all existing nano-sized metal oxides by using neural network method. Nanotoxicology 2017, 11, 475–483.
Basant, N.; Gupta, S. Multi-target QSTR modeling for simultaneous prediction of multiple toxicity endpoints of nano-metal oxides. Nanotoxicology 2017, 11, 339–350.
Zhou, Z.; Tang, X.; Dai, W.; Shi, J.; Chen, H. Nano-QSAR models for predicting cytotoxicity of metal oxide nanoparticles (MONPs) to E. coli. Can. J. Chem. 2017, 95, 863–866.
Kaweeteerawat, C.; Ivask, A.; Liu, R.; Zhang, H.; Chang, C.H.; Low-Kam, C.; Fischer, H.; Ji, Z.; Pokhrel, S.; Cohen, Y.; et al. Toxicity of metal oxide nanoparticles in Escherichia coli correlates with conduction band and hydration energies. Environ. Sci. Technol. 2015, 49, 1105–1112.
Gajewicz, A.; Schaeublin, N.; Rasulev, B.; Hussain, S.; Leszczynska, D.; Puzyn, T.; Leszczynski, J. Towards understanding mechanisms governing cytotoxicity of metal oxides nanoparticles: Hints from nano-QSAR studies. Nanotoxicology 2015, 9, 313–325.
Choi, J.S.; Trinh, T.X.; Yoon, T.H.; Kim, J.; Byun, H.G. Quasi-QSAR for predicting the cell viability of human lung and skin cells exposed to different metal oxide nanomaterials. Chemosphere 2019, 217, 243–249.
Yang, X.; Liu, J.; He, H.; Zhou, L.; Gong, C.; Wang, X.; Yang, L.; Yuan, J.; Huang, H.; He, L. SiO2 nanoparticles induce cytotoxicity and protein expression alteration in HaCaT cells. Part. Fibre Toxicol. 2010, 7, 1.
Comfort, K.K.; Maurer, E.I.; Hussain, S.M. Slow release of ions from internalized silver nanoparticles modifies the epidermal growth factor signaling response. Colloids Surf. B 2014, 123, 136–142.
Liu, R.; Rallo, R.; George, S.; Ji, Z.; Nair, S.; Nel, A.E.; Cohen, Y. Classification NanoSAR development for cytotoxicity of metal oxide nanoparticles. Small 2011, 7, 1118–1126.
Sizochenko, N.; Rasulev, B.; Gajewicz, A.; Mokshyna, E.; Kuz’min, V.E.; Leszczynski, J.; Puzyn, T. Causal inference methods to assist in mechanistic interpretation of classification nano-SAR models. RSC Adv. 2015, 5, 77739–77745.
Liu, R.; Zhang, H.Y.; Ji, Z.X.; Rallo, R.; Xia, T.; Chang, C.H.; Nel, A.; Cohen, Y. Development of structure-activity relationship for metal oxide nanoparticles. Nanoscale 2013, 5, 5644–5653.
Toropova, A.; Toropov, A.; Benfenati, E.; Korenstein, R.; Leszczynska, D.; Leszczynski, J. Optimal nano-descriptors as translators of eclectic data into prediction of the cell membrane damage by means of nano metal-oxides. Environ. Sci. Pollut. Res. Int. 2015, 22, 745–757.
Patel, T.; Telesca, D.; Low-Kam, C.; Ji, Z.; Zhang, H.Y.; Xia, T.; Zinc, J.I.; Nel, A.E. Relating nano-particle properties to biological outcomes in exposure escalation experiments. Environmetrics 2013, 25, 57–68.
Akhtar, M.J.; Ahamed, M.; Kumar, S.; Khan, M.M.; Ahmad, J.; Alrokayan, S.A. Zinc oxide nanoparticles selectively induce apoptosis in human cancer cells through reactive oxygen species. Int. J. Nanomed. 2012, 7, 845e857.
Xiong, S.; George, S.; Yu, H.; Damoiseaux, R.; France, B.; Ng, K.W.; Loo, J.S. Size influences the cytotoxicity of poly (lactic-co-glycolic acid)(PLGA) and titanium dioxide (TiO2) nanoparticles. Arch. Toxicol. 2013, 87, 1075e1086.
Forest, V.; Hochepied, J.-F.; Leclerc, L.; Trouvé, A.; Abdelkebir, K.; Sarry, G.; Augusto, V.; Pourchez, J. Towards an alternative to nano-QSAR for nanoparticle toxicity ranking in case of small datasets. J. Nanopart. Res. 2019, 21, 95.
Sayes, C.; Ivanov, I. Comparative study of predictive computational models for nanoparticle-induced cytotoxicity. Risk Anal. 2010, 30, 1723–1734.
Papa, E.; Doucet, J.P.; Doucet-Panaye, A. Linear and non-linear modelling of the cytotoxicity of TiO2 and ZnO nanoparticles by empirical descriptors. SAR QSAR Environ. Res. 2015, 26, 647–665.
Fourches, D.; Pu, D.; Tassa, C.; Weissleder, R.; Shaw, S.Y.; Mumper, R.J.; Tropsha, A. Quantitative nanostructure-activity relationship modeling. ACS Nano 2010, 4, 5703–5712.
Shaw, S.Y.; Westly, E.C.; Pittet, M.J.; Subramanian, A.; Schreiber, S.L.; Weissleder, R. Perturbational profiling of nanomaterial biologic activity. Proc. Natl. Acad. Sci. USA 2008, 105, 7387–7392.
Weissleder, R.; Kelly, K.; Sun, E.Y.; Shtatland, T.; Josephson, L. Cell-specific targeting of nanoparticles by multivalent attachment of small molecules. Nat. Biotechnol. 2005, 23, 1418–1423.
Epa, V.C.; Burden, F.R.; Tassa, C.; Weissleder, R.; Shaw, S.; Winkler, D.A. Modeling biological activities of nanoparticles. Nano Lett. 2012, 12, 5808–5812.
Liu, R.; Rallo, R.; Weissleder, R.; Tassa, C.; Shaw, S.; Cohen, Y. Nano-SAR development for bioactivity of nanoparticles with considerations of decision boundaries. Small 2013, 9, 1842–1852.
Liu, X.; Tang, K.; Harper, S.; Harper, B.; Steevens, J.A.; Xu, R. Predictive modeling of nanomaterial exposure effects in biological systems. Int. J. Nanomed. 2013, 8, 31–43.
Luan, F.; Kleandrova, V.V.; González-Díaz, H.; Ruso, J.M.; Melo, A.; Speck-Planche, A.; Cordeiro, M.N. Computer-aided nanotoxicology: Assessing cytotoxicity of nanoparticles under diverse experimental conditions by using a novel QSTR-perturbation approach. Nanoscale 2014, 6, 10623–10630.
Kleandrova, V.V.; Luan, F.; González-Díaz, H.; Ruso, J.M.; Speck-Planche, A.; Cordeiro, M.N. Computational tool for risk assessment of nanomaterials: Novel QSTR-perturbation model for simultaneous prediction of ecotoxicity and cytotoxicity of uncoated and coated nanoparticles under multiple experimental conditions. Environ. Sci. Technol. 2014, 48, 14686–14694.
Kleandrova, V.V.; Luan, F.; González-Díaz, H.; Ruso, J.M.; Melo, A.; Speck-Planche, A.; Cordeiro, M.N. Computational ecotoxicology: Simultaneous prediction of ecotoxic effects of nanoparticles under different experimental conditions. Environ. Int. 2014, 73, 288–294.
Concu, R.; Kleandrova, V.V.; Speck-Planche, A.; Cordeiro, M.N.D.S. Probing the toxicity of nanoparticles: A unified in silico machine learning model based on perturbation theory. Nanotoxicology 2017, 11, 891–906.
Chen, G.; Vijver, M.G.; Peijnenburg, W.J. Summary and analysis of the currently existing literature data on metal-based nanoparticles published for selected aquatic organisms: Applicability for toxicity prediction by (Q)SARs. Altern. Lab. Anim. 2015, 43, 221–240.
Chen, G.; Peijnenburg, W.J.; Kovalishyn, V.; Vijver, M.G. Development of nanostructure-activity relationships assisting the nanomaterial hazard categorization for risk assessment and regulatory decision-making. RSC Adv. 2016, 6, 52227–52235.
Mikolajczyk, A.; Sizochenko, N.; Mulkiewicz, E.; Malankowska, A.; Nischk, M.; Jurczak, P.; Hirano, S.; Nowaczyk, G.; Zaleska-Medynska, A.; Leszczynski, J.; et al. Evaluating the toxicity of TiO(2)-based nanoparticles to Chinese hamster ovary cells and Escherichia coli: A complementary experimental and computational approach. Beilstein J. Nanotechnol. 2017, 8, 2171–2180.
Nymark, P.; Jensen, K.A.; Suhonen, S.; Kembouche, Y.; Vippola, M.; Kleinjans, J.; Catalán, J.; Norppa, H.; van Delft, J.; Briedé, J.J. Free radical scavenging and formation by multi-walled carbon nanotubes in cell free conditions and in human bronchial epithelial cells. Part. Fibre Toxicol. 2014, 11, 4.
Toropov, A.A.; Toropova, A.P. Quasi-QSAR for mutagenic potential of multi-walled carbon-nanotubes. Chemosphere 2015, 124, 40–46.
Wirnitzer, U.; Herbold, B.; Voetz, M.; Ragot, J. Studies on the in vitro genotoxicity of baytubes, agglomerates of engineered multi-walled carbonnanotubes (MWCNT). Toxicol. Lett. 2009, 186, 160–165.
Toropova, A.P.; Toropov, A.A.; Rallo, R.; Leszczynska, D.; Leszczynski, J. Nano-QSAR: Genotoxicity of Multi-Walled Carbon Nanotubes. Int. J. Environ. Res. 2016, 10, 59–64.
Ema, M.; Imamura, T.; Suzuki, H.; Kobayashi, N.; Naya, M.; Nakanishi, J. Evaluation of genotoxicity of multiwalled carbon nanotubes in a battery of in vitro and in vivo assays. Regul. Toxicol. Pharmacol. 2012, 63, 188–195.
Toropov, A.A.; Toropova, A.P. Quasi-SMILES and nano-QFAR: United model for mutagenicity of fullerene and MWCNT under different conditions. Chemosphere 2015, 139, 18–22.
Shinohara, N.; Matsumoto, K.; Endoh, S.; Maru, J.; Nakanishi, J. In vitro and in vivo genotoxicity tests on fullerene C60 nanoparticles. Toxicol. Lett. 2009, 191, 289–296.
Trinh, T.X.; Choi, J.S.; Jeon, H.; Byun, H.G.; Yoon, T.H.; Kim, J. Quasi-SMILES-based nano-quantitative structure-activity relationship model to predict the cytotoxicity of multiwalled carbon nanotubes to human lung cells. Chem. Res. Toxicol. 2018, 31, 183–190.
Toropov, A.A.; Toropova, A.P. Optimal descriptor as a translator of eclectic data into endpoint prediction: Mutagenicity of fullerene as a mathematical function of conditions. Chemosphere 2014, 104, 262–264.
Toropova, A.P.; Toropov, A.A.; Veselinović, A.M.; Veselinović, J.B.; Benfenati, E.; Leszczynska, D.; Leszczynski, J. Nano-QSAR: Model of mutagenicity of fullerene as a mathematical function of different conditions. Ecotox. Environ. Safe. 2016, 124, 32–36.
Manganelli, S.; Leone, C.; Toropov, A.A.; Toropova, A.P.; Benfenati, E. QSAR model for predicting cell viability of human embryonic kidney cells exposed to SiO₂ nanoparticles. Chemosphere 2016, 144, 995–1001.
Wang, F.; Gao, F.; Lan, M.; Yuan, H.; Huang, Y.; Liu, J. Oxidative stress contributes to silica nanoparticle-induced cytotoxicity in human embryonic kidney cells. Toxicol. Vitr. 2009, 23, 808–815.
Toropova, A.P.; Toropov, A.A.; Benfenati, E. A quasi-QSPR modelling for the photocatalytic decolourization rate constants and cellular viability (CV%) of nanoparticles by CORAL. SAR QSAR Environ. Res. 2015, 26, 29–40.
Passagne, I.; Morille, M.; Rousset, M.; Pujalté, I.L.; L’Azou, B. Implication of oxidative stress in size-dependent toxicity of silica nanoparticles in kidney cells. Toxicology 2012, 299, 112–124.
Cassano, A.; Marchese Robinson, R.L.; Palczewska, A.; Puzyn, T.; Gajewicz, A.; Tran, L.; Manganelli, S.; Cronin, M.T. Comparing the CORAL and Random Forest approaches for modelling the in vitro cytotoxicity of silica nanomaterials. Altern. Lab. Anim. 2016, 44, 533–556.
Manganelli, S.; Benfenati, E. Nano-QSAR model for predicting cell viability of human embryonic kidney cells. Methods Mol. Biol. 2017, 1601, 275–290.