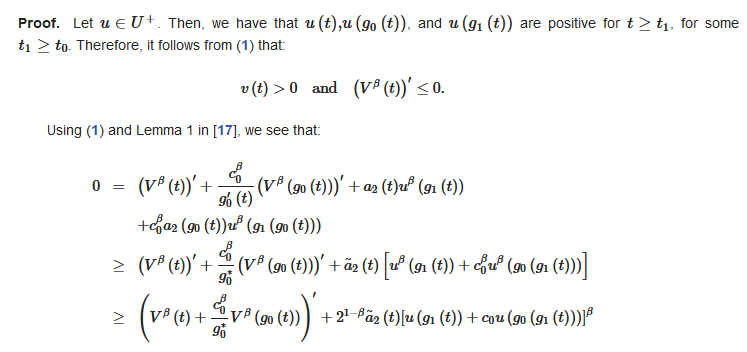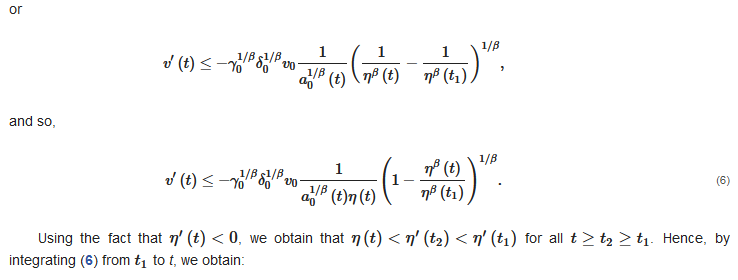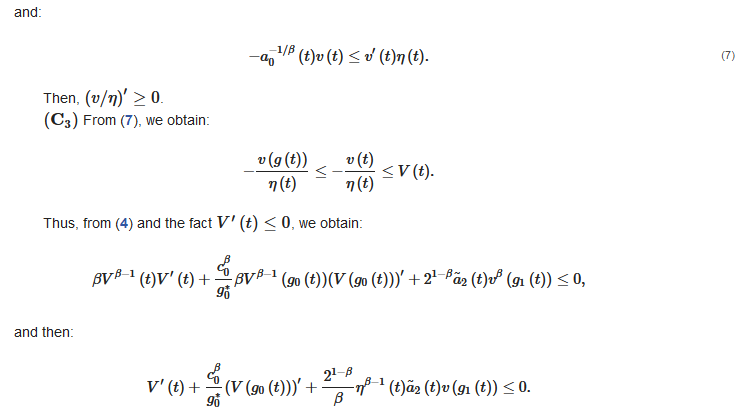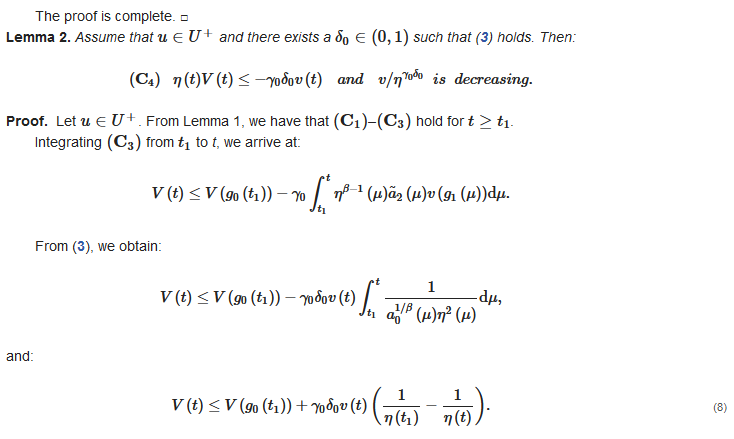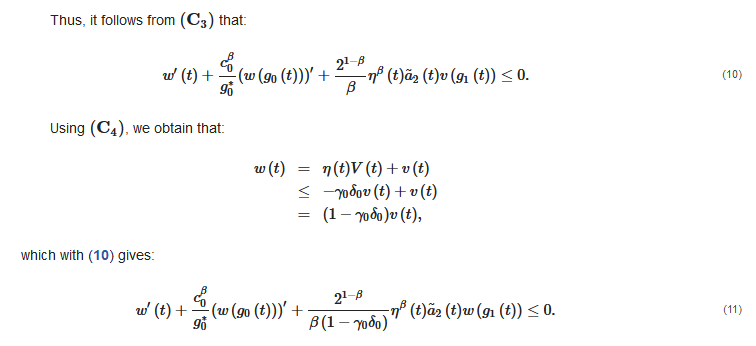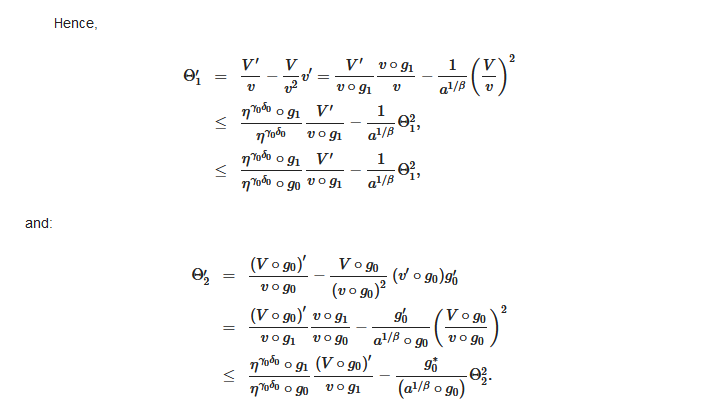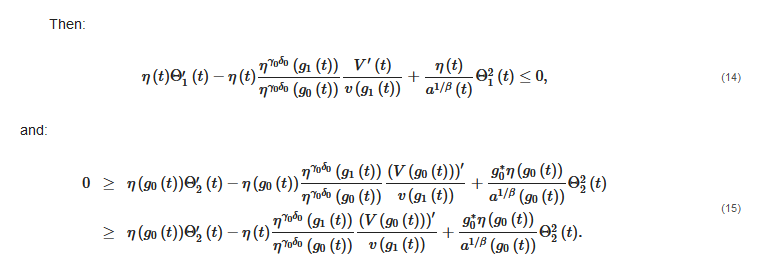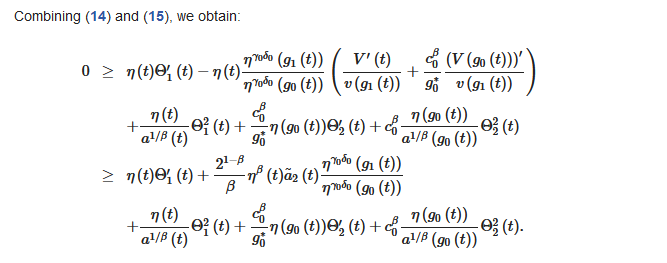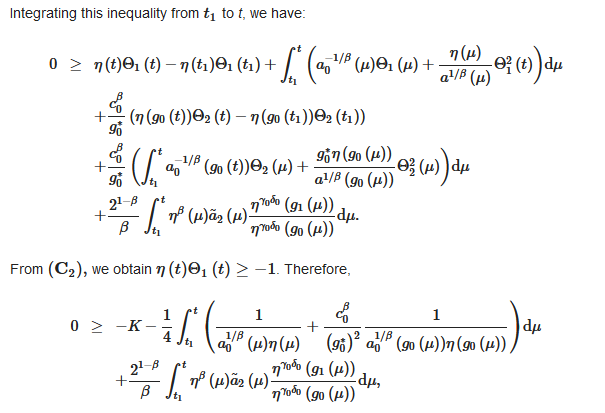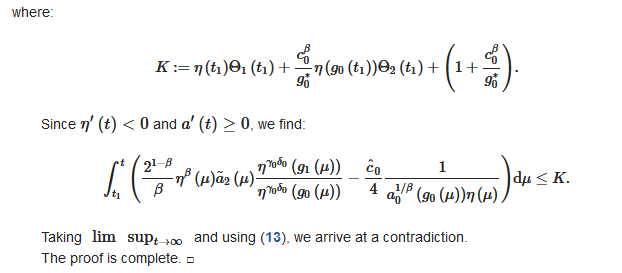A DDE is a single-variable differential equation, usually called time, in which the derivative of the solution at a certain time is given in terms of the values of the solution at earlier times. Moreover, if the highest-order derivative of the solution appears both with and without delay, then the DDE is called of the neutral type. The neutral DDEs have many interesting applications in various branches of applied science, as these equations appear in the modeling of many technological phenomena. The problem of studying the oscillatory and nonoscillatory properties of DDEs has been a very active area of research in the past few decades.
- delay differential equation
- neutral
- oscillation
- noncanonical case
1. Introduction
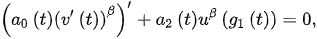
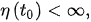
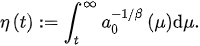
2. Oscillatory Properties of Noncanonical Neutral DDEs of Second-Order
We begiCon wsith the following notations: is thder the 2nd-order set of all eventually positive solutions of delay differential equation (1DDE), ,
Lemma 1. Assumeof thate and there exists a such that:
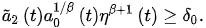
(3)
Then, vral eventually satisfiesype:

and:
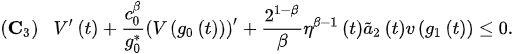
Proof. Let . Then, we have that , and are poscitive forllatory , fopr some . Theperefore, it follows from (1) that:
Using (1) and Lemma 1 in [1], we see that:

and of so:
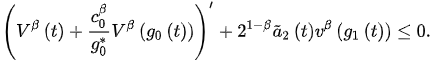
(4)
Integrating this inequality from to t and using the fact , we find:
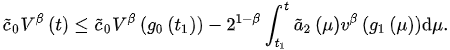
(5)
Assume the contrary, that for . Thus, from (5), we have:
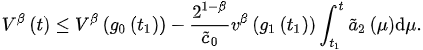
This, ofrom (3), implies:
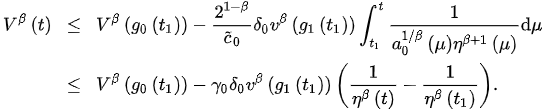
Letting and taking the fact that as , we obtain , which cd-ontradicts the positivity of .
Next, sider nce v is positive decreasing, we have that . Assume the contrary, that . Then, for alral , forDDE some . Thus, from (31) and (5), we have:
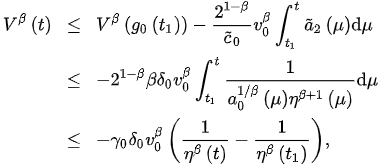
or
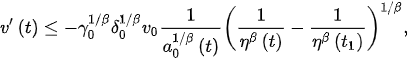
and so,
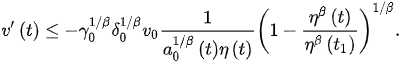
(6)
Using the fact that noncanonical case, we obtain that for all . Hence, by integrating (6) from to t, we obtains:

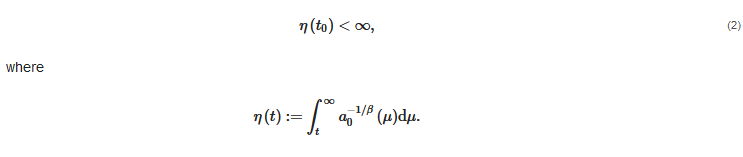
Lett
2. Oscillatory Properties of Noncanonical Neutral DDEs of Second-Order

2.1. Auxiliary Lemmas

2.2. Oscillation Theorems
ing and taking the fact that as , wne obxtain , which contradicts the positivity of . Theoreforem, .
Sinceby ius decreasing, we obtain:
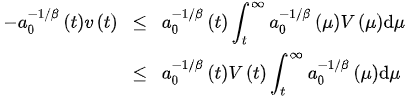
and:
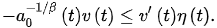
(7)
T then, .
Fprom (7), we obtain:
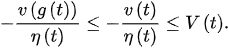
Thus, from (4) and the fact , we obtain:

and then:
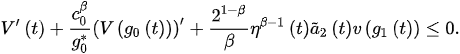
Thple proof is complete.
Lemma 2. Acomparissumeon thatwith and there exists a sequch that (3) hiolds. Then:
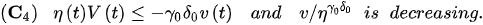
Proof. Let . Fromf Lemma 1, we have that – hold the for .
Integrating from st-o t, we arrive at:
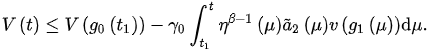
Frderom (3), we obtain:
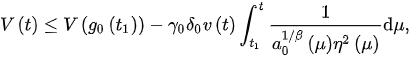
and:
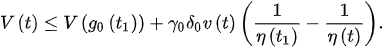
(8)
Using , we eventually have:
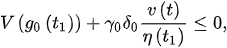
Hence, (8)w becomes:
Thris implies that is a decreasing function.
The pion foroof is complete.
2.2. Oscillation Theorems
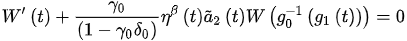
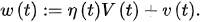 From , for . Thus,
From , for . Thus,
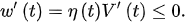 Thus, it follows from that:
Thus, it follows from that:
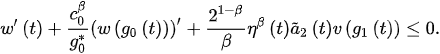
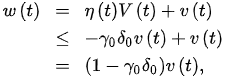 which with (10) gives:
which with (10) gives:
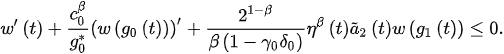
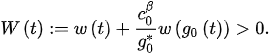 Then, , and so, (11) becomes:
which has a positive solution. In view of [2] (Theorem 1), (9) also has a positive solution, which is a contradiction.
The proof is complete.
Corollary 1. Assume that and there exists a such that (3) holds. If:
Then, , and so, (11) becomes:
which has a positive solution. In view of [2] (Theorem 1), (9) also has a positive solution, which is a contradiction.
The proof is complete.
Corollary 1. Assume that and there exists a such that (3) holds. If:
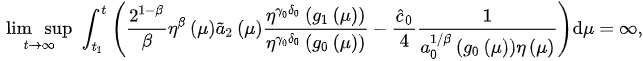
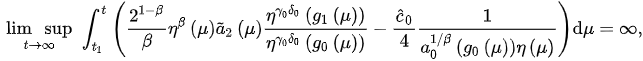
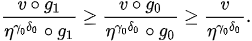 Hence,
Hence,
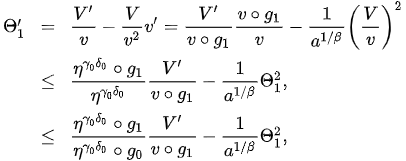 and:
and:
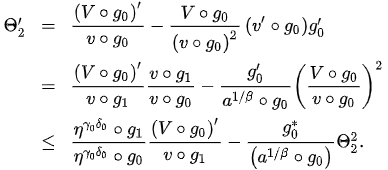 Then:
Then:
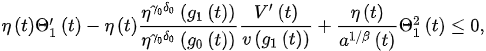
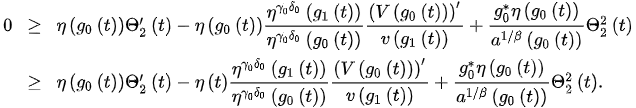
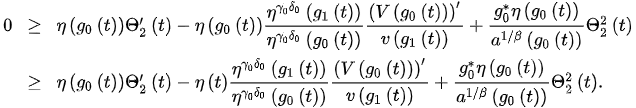 Integrating this inequality from to t, we have:
Integrating this inequality from to t, we have:
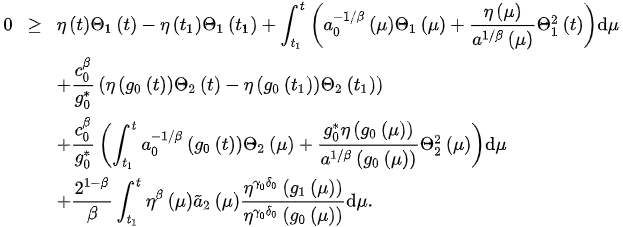 From we obtain . Therefore,
where:
From we obtain . Therefore,
where:
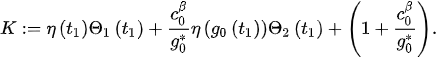 Since and , we find:
Taking and using (13), we arrive at a contradiction.
The proof is complete.
Since and , we find:
Taking and using (13), we arrive at a contradiction.
The proof is complete.
2.3. Applications and Discussion
Remark 1. It is easy to see that tthe previous works that dealt with the noncanonical case required either scillatior . Since η is decreasing and , we have that . Then, the results of these works only apply when (1).
Example

2.3. Applications


1. Consider the DDE:
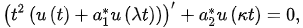
(16)
where and . By choosing the condition (12) becomes: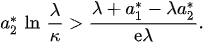
 A simple computation shows that (16) is oscillatory if:
A simple computation shows that (16) is oscillatory if:
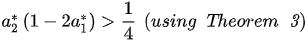

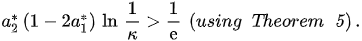
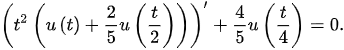
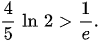 which ensures the oscillation of (21).
which ensures the oscillation of (21).