Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 1 by Wenyue Wang and Version 2 by Peter Tang.
The vector optical beam with longitudinally varying polarization during propagation in free space has attracted significant attention in recent years. Compared with traditional vector optical beams with inhomogeneous distribution of polarization in the transverse plane, manipulating the longitudinal distribution of polarization provides a new dimension for the expansion of the applications of vector optical beams in volume laser machining, longitudinal detection, and in vivo micromanipulation.
- vector optical beam
- structured light
- Bessel beam
- Poincaré sphere
1. Introduction
Unlike the scalar optical beam with a homogeneous state of polarization (SoP), the vector optical beam [1], with spatially inhomogeneous distributions of polarization, has attracted increasing interest in recent years due to the unique spatial structure of polarization which has a significant influence on the spatio-temporal evolution of light and the interactions between light and matter. It has been demonstrated that the vector beams can shape the focal field [2][3][2,3], control optical nonlinear processes [4][5][4,5], enhance the longitudinal component [6], and induce strong magnetic impulses [7]. These features raise the prospect of using vector beams in quantum information [8], single molecule imaging [9], particle acceleration [10], nonlinear optics [11], optical microfabrication [12][13][12,13], optical micromanipulation, and optical tweezers [14][15][14,15].
As one type of structured light [16], the vector beam is supported by spatial manipulation technology of the optical beam. Polarization is an important vector property of light and provides a degree of freedom for customization of the optical beam. Compared with the manipulation of the amplitude and phase distribution in one optical field, the modulation of polarization is more complex. The flexibility of vector beams has been a problem for a long time. Over the past few years, the passive generation method, based on electro-optical modulation outside the resonator [17][18][17,18], which effectively promotes the flexibility of polarization manipulation in free space and the diversity of vector optical beams, has developed rapidly [19][20][21][22][23][24][19,20,21,22,23,24].
Previous studies of vector beams have mostly focused on the polarization distribution in the transverse plane. In addition to the well-known azimuthally and radially varying vector optical field (VOFs) [25], many special transverse distributions, such as bipolar- [26], parabolic- [27] and elliptic- [28] symmetry, double-mode [18], and fractal VOFs, [29] have been generated. However, with a degree of spatial freedom, the propagation direction is also a significant dimension to construct inhomogeneous distributions of polarization. The unique beam, with customized polarization distribution in the longitudinal direction, was first generated in 2015 [30] and has attracted increasing attention in recent years. Beyond enriching the forms of vector beam, the variation of polarization along the direction of propagation provides increased scope for the interaction between light and matter, especially in nonlinear effect and spin–orbit coupling. Moreover, it also offers advantages in the applications of material deep processing, remote polarimetry, and three-dimensional micromanipulation. In order to realize the variation of polarization in the longitudinal direction, a direct method is to modulate the propagation environment of the polarized beam, including by artificially constructing the anisotropic media with a spatially modulated optic axis [31][32][33][34][31,32,33,34], or by utilizing the self-induced nonlinear effects of optical beams in a nonlinear medium [35][36][37][38][35,36,37,38]. However, for situations in which the propagation environment cannot be manipulated, such as in free space, the direct methods are unsuitable and the possibility of modulating the beam at the initial plane to indirectly control the longitudinal distribution of polarization should be taken into consideration. In recent years, many indirect methods have been proposed to generate vector optical beams with longitudinally varying polarization in free space based on different theoretical and experimental strategies. The schematic diagram of vector optical beams with longitudinally varying polarization in free space is shown in Figure 1.

Figure 1.
Schematic diagram of the longitudinal variation of polarization in free space.
2. The Principle of Generating Vector Optical Beams with Polarization Varying along a Longitudinal Direction in Free Space
An arbitrary vector optical beam can be divided into two components with different polarization and complex amplitude [18]. Using VOFs with transverse distribution of polarization as examples, the VOF can be generally expressed as
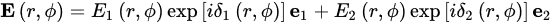
where r and ϕ are the radial and azimuthal coordinates, E1 and E2 are the amplitude distributions of these two beams, δ1 and δ2 are the phase distributions, and e1 and e2 represent orthogonal polarization base vectors. The complex spatial distribution of polarization in VOF, from another perspective, originates from the superposition of two orthogonally polarized beams with different complex amplitude distributions. The difference may occur in the amplitude, phase, or both. For example, assuming two superposed beams are carrying left- and right-hand circular polarizations and their amplitudes are the same, but the phase distributions are different δ1 = –δ2 = ϕ. In this configuration, the superposition of these two beams leads to the generation of localized linear-polarized VOF. If the phase distributions are the same but the amplitudes of the two beams are E1 = cosϕ and E2 = sinϕ, localized linear-polarized VOF can also be generated when the polarization of the two beams are orthogonally linear-polarized. Therefore, to generate the vector optical beam with varying polarization along the longitudinal direction in free space, there are two strategies available: constructing the longitudinally varying phase difference and amplitude difference, respectively.
3. The Experimental Generation of Vector Optical Beams with Longitudinally Varying Polarization in Free Space
Unlike the traditional VOF with transverse polarization distribution, controlling the longitudinal distribution of polarization in free space requires an indirect modulation method. The controllable and flexible variation of polarization in the longitudinal direction has always been sought and much effort has been spent on the generation method of this special vector beam in recent years. The controllability reflects the accuracy and predictability of polarization at each propagation position, while the flexibility implies the diverse and adjustable distribution of polarization in the longitudinal direction. The generation methods in free space can be broadly divided into the modulation of complex amplitude in real space and the filtering of the spatial spectrum.3.1. Modulation on the Complex Amplitude in Real Space
In order to generate the beam whose polarization varies with propagation distance in free space, one approach is to modulate the initial phase distribution. The phase modulation determines the transverse component of the wave vector and will further influence the longitudinal component kz. If two collinear orthogonally polarized optical beams have different kz, a dynamic phase difference as a function of propagation distance will appear, which drives the variation of polarization during propagation. It is found that the initial phase modulation of two collinear polarized beams can be implemented based on the phase masks and the holographic grating.
 A quasi-Bessel beam composed of two orthogonally polarized beams with linearly varying axial intensity, for which the axial fields can be expressed as
A quasi-Bessel beam composed of two orthogonally polarized beams with linearly varying axial intensity, for which the axial fields can be expressed as
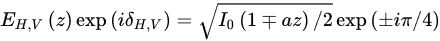 where a is a constant determining the varying period. With the axial intensities of two polarization components constantly varying, the polarization also changes correspondingly. The results at z = −15, −10, 0, 10, 15 cm are measured respectively, and the ellipticity of the polarization experiences a variation from increase to decrease, thereby the transformation of the polarization of this quasi-Bessel beam continuously moving along the meridian of the Poincaré sphere. More importantly, because of the complementary axial intensity distributions of these two polarization components, the total axial intensity has an approximately uniform profile in the non-diffractive region. Nevertheless, the variation of the ellipticity angle varies with different angles when propagating over the same distance. In order to achieve uniform variation of polarization, another axial envelope is designed as
where a is a constant determining the varying period. With the axial intensities of two polarization components constantly varying, the polarization also changes correspondingly. The results at z = −15, −10, 0, 10, 15 cm are measured respectively, and the ellipticity of the polarization experiences a variation from increase to decrease, thereby the transformation of the polarization of this quasi-Bessel beam continuously moving along the meridian of the Poincaré sphere. More importantly, because of the complementary axial intensity distributions of these two polarization components, the total axial intensity has an approximately uniform profile in the non-diffractive region. Nevertheless, the variation of the ellipticity angle varies with different angles when propagating over the same distance. In order to achieve uniform variation of polarization, another axial envelope is designed as
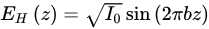
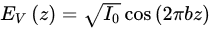 The distributions of Stokes parameters at z = 0, 1.9, 3.8, 5.6, and 7.5 cm are measured. The results demonstrate the quasi-Bessel beam retains a linear polarization upon propagation that shows a periodic variation of polarization along the equator of the Poincaré sphere.
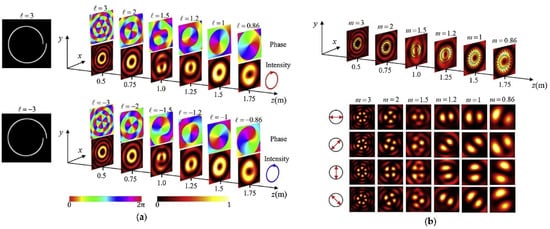
Recently, a theoretical model to obtain anomalous VBBs with varying polarization order during propagation was demonstrated by Liu et al. [44][65]. Compared with changing the charge of VOF by dividing the axicon into various radial sectors [45][49], the method introduced a continuous phase delay by designed spiral slits [46][47][66,67] is more flexible such that arbitrary polarization orders, including integers and fractions, can be generated along the propagation axis. This approach was inspired by the idea that a zeroth-order Bessel beam can be thought of as the Fourier transform of an annular slit [48][68]. The diffraction intensity distributions and phase profiles of anomalous Bessel beams at different propagation distances are shown in Figure 3a. A right-/left-handed circularly polarized plane wave illuminates the spiral slit corresponding to l = 3 and −3, respectively. It can be observed that the topological charge of the anomalous Bessel vortex beam decreases with the propagation distance. When these two beams are collinearly superposed, the generated anomalous VBB is shown in Figure 3b. With the gradual increase of the propagation distance, the polarization order of the anomalous VBB will gradually tend to zero accompanied by the variation of polarization distribution. This characteristic may provide more possibilities and expand the applications in optical trapping, quantum communications, and optical microscopy.
The distributions of Stokes parameters at z = 0, 1.9, 3.8, 5.6, and 7.5 cm are measured. The results demonstrate the quasi-Bessel beam retains a linear polarization upon propagation that shows a periodic variation of polarization along the equator of the Poincaré sphere.
Recently, a theoretical model to obtain anomalous VBBs with varying polarization order during propagation was demonstrated by Liu et al. [44][65]. Compared with changing the charge of VOF by dividing the axicon into various radial sectors [45][49], the method introduced a continuous phase delay by designed spiral slits [46][47][66,67] is more flexible such that arbitrary polarization orders, including integers and fractions, can be generated along the propagation axis. This approach was inspired by the idea that a zeroth-order Bessel beam can be thought of as the Fourier transform of an annular slit [48][68]. The diffraction intensity distributions and phase profiles of anomalous Bessel beams at different propagation distances are shown in Figure 3a. A right-/left-handed circularly polarized plane wave illuminates the spiral slit corresponding to l = 3 and −3, respectively. It can be observed that the topological charge of the anomalous Bessel vortex beam decreases with the propagation distance. When these two beams are collinearly superposed, the generated anomalous VBB is shown in Figure 3b. With the gradual increase of the propagation distance, the polarization order of the anomalous VBB will gradually tend to zero accompanied by the variation of polarization distribution. This characteristic may provide more possibilities and expand the applications in optical trapping, quantum communications, and optical microscopy.
3.2. Filtering of Spatial Spectrum
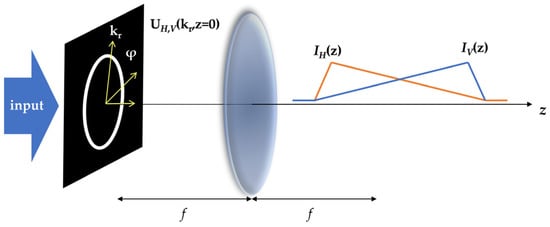
Phase modulation in real space is the commonly used method to manipulate the polarization distribution both in the transverse and longitudinal directions. However, for the vector optical beam with varying polarization along propagation direction in free space, the initial phase modulation will inevitably influence the intensity distribution of the propagating field. In order to improve the axial intensity distribution of the generated beams with longitudinally varying polarization, Zhao et al. utilized the Sagnac interferometer [19][39][40][41][19,56,61,62] to construct the superposition of two beams with complementary axial intensities and orthogonal SoPs based on the spatial spectrum optimization approach proposed by Cižmár and Dholakia [42][47], thereby generating a quasi-Bessel beam with uniform axial intensity but varying polarization upon propagation [43][46]. The schematic of the theoretical configuration is shown in Figure 2.
Figure 2. Schematic of the theoretical configuration of reshaping the axial intensity distributions of quasi-Bessel beams [43].
Schematic of the theoretical configuration of reshaping the axial intensity distributions of quasi-Bessel beams [46].
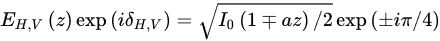 where a is a constant determining the varying period. With the axial intensities of two polarization components constantly varying, the polarization also changes correspondingly. The results at z = −15, −10, 0, 10, 15 cm are measured respectively, and the ellipticity of the polarization experiences a variation from increase to decrease, thereby the transformation of the polarization of this quasi-Bessel beam continuously moving along the meridian of the Poincaré sphere. More importantly, because of the complementary axial intensity distributions of these two polarization components, the total axial intensity has an approximately uniform profile in the non-diffractive region. Nevertheless, the variation of the ellipticity angle varies with different angles when propagating over the same distance. In order to achieve uniform variation of polarization, another axial envelope is designed as
where a is a constant determining the varying period. With the axial intensities of two polarization components constantly varying, the polarization also changes correspondingly. The results at z = −15, −10, 0, 10, 15 cm are measured respectively, and the ellipticity of the polarization experiences a variation from increase to decrease, thereby the transformation of the polarization of this quasi-Bessel beam continuously moving along the meridian of the Poincaré sphere. More importantly, because of the complementary axial intensity distributions of these two polarization components, the total axial intensity has an approximately uniform profile in the non-diffractive region. Nevertheless, the variation of the ellipticity angle varies with different angles when propagating over the same distance. In order to achieve uniform variation of polarization, another axial envelope is designed as
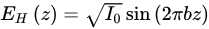
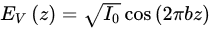 The distributions of Stokes parameters at z = 0, 1.9, 3.8, 5.6, and 7.5 cm are measured. The results demonstrate the quasi-Bessel beam retains a linear polarization upon propagation that shows a periodic variation of polarization along the equator of the Poincaré sphere.
Recently, a theoretical model to obtain anomalous VBBs with varying polarization order during propagation was demonstrated by Liu et al. [44][65]. Compared with changing the charge of VOF by dividing the axicon into various radial sectors [45][49], the method introduced a continuous phase delay by designed spiral slits [46][47][66,67] is more flexible such that arbitrary polarization orders, including integers and fractions, can be generated along the propagation axis. This approach was inspired by the idea that a zeroth-order Bessel beam can be thought of as the Fourier transform of an annular slit [48][68]. The diffraction intensity distributions and phase profiles of anomalous Bessel beams at different propagation distances are shown in Figure 3a. A right-/left-handed circularly polarized plane wave illuminates the spiral slit corresponding to l = 3 and −3, respectively. It can be observed that the topological charge of the anomalous Bessel vortex beam decreases with the propagation distance. When these two beams are collinearly superposed, the generated anomalous VBB is shown in Figure 3b. With the gradual increase of the propagation distance, the polarization order of the anomalous VBB will gradually tend to zero accompanied by the variation of polarization distribution. This characteristic may provide more possibilities and expand the applications in optical trapping, quantum communications, and optical microscopy.
The distributions of Stokes parameters at z = 0, 1.9, 3.8, 5.6, and 7.5 cm are measured. The results demonstrate the quasi-Bessel beam retains a linear polarization upon propagation that shows a periodic variation of polarization along the equator of the Poincaré sphere.
Recently, a theoretical model to obtain anomalous VBBs with varying polarization order during propagation was demonstrated by Liu et al. [44][65]. Compared with changing the charge of VOF by dividing the axicon into various radial sectors [45][49], the method introduced a continuous phase delay by designed spiral slits [46][47][66,67] is more flexible such that arbitrary polarization orders, including integers and fractions, can be generated along the propagation axis. This approach was inspired by the idea that a zeroth-order Bessel beam can be thought of as the Fourier transform of an annular slit [48][68]. The diffraction intensity distributions and phase profiles of anomalous Bessel beams at different propagation distances are shown in Figure 3a. A right-/left-handed circularly polarized plane wave illuminates the spiral slit corresponding to l = 3 and −3, respectively. It can be observed that the topological charge of the anomalous Bessel vortex beam decreases with the propagation distance. When these two beams are collinearly superposed, the generated anomalous VBB is shown in Figure 3b. With the gradual increase of the propagation distance, the polarization order of the anomalous VBB will gradually tend to zero accompanied by the variation of polarization distribution. This characteristic may provide more possibilities and expand the applications in optical trapping, quantum communications, and optical microscopy.

Figure 3. (a) The diffraction intensity distributions and phase profiles of anomalous Bessel beams under different propagation distances. (b) The intensity and polarization distribution of the generated anomalous VBBs at different propagation distances. Adapted with permission from [44][65], copyrighter Elsevier, 2021.
