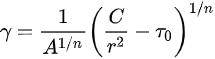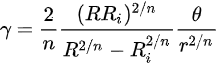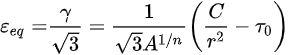Principle of tube high-pressure shearing
The principle of t-HPS is depicted schematically in Figure 1 where the sample, in the form of a tube, is radially confined between a central mandrel and an outer cylinder. The principle of the process is that a sufficiently high hydrostatic pressure is introduced in the tube wall so that the frictional forces at the interfaces between the sample-mandrel and the sample-cylinder are high enough to prevent any localized slip. By fixing the mandrel and rotating the outer cylinder (or vice versa), a simple shear strain is then produced in the tube wall.
Figure 1. Schematic illustration of the principles of t-HPS
A critical factor determining the success of t-HPS is to obtain a sufficiently high hydrostatic pressure in the tube wall confined between the central mandrel and the outer cylinder. Different procedures may be adopted for introducing a hydrostatic pressure into the tube wall. A radial force may be applied at the cylinder surface by, for example, compressing the mandrel within the elastic regime. An alternative and attractive procedure is to apply an axial force at the two ends of the tube. This may be accomplished by fully confining the tube through the use of pressure rings at both ends of the sample and then compressing the rings directly to build up a high hydrostatic pressure in the tube wall as illustrated in Figure 1.
The average strain, γ, introduced into the tube wall is:

where Ri and R are the inner and outer radii of the tube respectively.
The strain distribution in fact in tube wall is not uniform and a strain gradient exists. For a constitutional equation in the form where τ0 and A are material constants and n the strain hardening exponent, the shear strain dependence on radical coordinate r is:
where τ0 and A are material constants and n the strain hardening exponent, the shear strain dependence on radical coordinate r is:
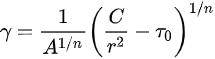
where C is integration constant. This leads to a simpler expression of shear strain γ for the special case of τ0 =0.
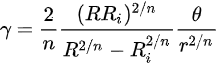
The average equivalent strain:

The equivalent strain distribution for materials with constitutional relation τ = τ0+Aγ n:
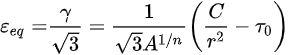
Or for the materials with simple constitutional relation τ = Aγ n:

It is clear that the strain distribution is materials dependent.
It should be noted that edge effect also appears as in other deformation processing [2].
t-HPS has been utilized to synthesis multilayered structures in one single step of t-HPS rotation [3].
The following is recent application t-HPS to process eutectic Bi–Sn (57/43) alloy for superplasticity [4].
[1] Wang, J.T.; Li, Z.; Wang, J.; Langdon, T.G. Principles of severe plastic deformation using tube high-pressure shearing. Scr. Mater. 2012, 67, 810–813.
[2] Meng, J.J.; Li, Z.; Liu, Y.; Bin Zhu, Y.; Wang, S.; Lin, K.; Tao, J.Q.; Wang, J.T. Investigation on the Strain Distribution in Tube High-Pressure Shearing. Metals 2019, 9, 1117.
[3] Li, Z.; Zhang, P.F.; Yuan, H.; Lin, K.; Liu, Y.; Yin, D.L.;Wang, J.T.; Langdon, T.G. Principle of one-step synthesis for multilayered structures using tube high-pressure shearing. Mater. Sci. Eng. A 2016, 658, 367–375.
[4] Wang, C.-T.; Li, Z.; He, Y.; Wang, J.-T.; Langdon, T.G. Microstructural Evolution and Tensile Testing of a Bi–Sn (57/43) Alloy Processed by Tube High-Pressure Shearing. Crystals 2021, 11, 1229.
----------------------------------------------------------------------------------------------------------------------
1. Introduction
Considerable interest has developed over the last two decades to producing and measuring the mechanical properties of materials with exceptionally small grain sizes. Ultrafine-grained (UFG) metals are defined specifically as metals where the average grain size is less than ~1 µm
[1] and these small grains divide into the two categories of submicrometer grains with sizes of 100–1000 nm and nanometer grains where the average size is <100 nm. An advantage in producing these materials is that they exhibit high strength and there is a potential for achieving superplastic elongations at exceptionally rapid strain rates which would be advantageous for manufacturing parts in the superplastic forming industry
[2]. Materials with UFG structures are generally produced using procedures based on the application of severe plastic deformation (SPD) where the material is subjected to a very high strain but without any significant changes in the overall dimensions of the workpiece. As discussed in a comprehensive review
[3], the two main techniques of SPD processing are equal channel angular pressing (ECAP), where a rod or a bar is pressed through a die constrained within a channel bent through a sharp angle
[4], and high-pressure torsion (HPT), where the sample is generally in the form of a thin disk subjected to high pressure and concurrent torsional straining
[5].
Both ECAP and HPT are effective for processing to produce metals with very small grains, but the procedures are different because ECAP is a discontinuous and labor-intensive process in which the sample is removed and then reinserted into the die between each pass whereas HPT is a continuous process where the sample is torsionally strained up to the required maximum numbers of rotations. In practice, the experiments show that processing by HPT has two advantages over ECAP because it produces smaller grain sizes
[6][7][6,7] and a larger fraction of grain boundaries with large angles of misorientation
[8][9][10][11][12][8,9,10,11,12]. Nevertheless, HPT processing has a significant disadvantage that it cannot be utilized in large-scale industrial applications.
2. Experimental Results
Figure 1 shows the microstructures of the Bi–Sn alloy (a) in the as-cast condition and after t-HPS processing for (b) 0.25, (c) 1, (d) 5 and (e) 20 turns, where the SEM observations were conducted after storage at RT for 8 h following t-HPS processing. Inspection showed the as-cast Bi–Sn alloy has a typical eutectic structure where the Bi phase and the Sn phase are complementary and packed together. As the etchant preferentially attacked the Sn phase, large amounts of very small Bi precipitate particles became visible within the Sn-rich areas after etching. After t-HPS processing for 0.25 and 1 turn, no significant microstructural change was observed despite some slight rotation of the lamellar structure, and the overall eutectic structure was not destroyed. As the number of turns increased to 5 and 20, it was observed that each phase started to fracture. The edges of both phases became sharper and grains with equiaxed shapes became visible.
Figure 1. Microstructure of the Bi–Sn samples in (a) the as-cast condition and after t-HPS processing for (b) 0.25, (c) 1, (d) 5 and (e) 20 turns and storage at RT for 8 h.
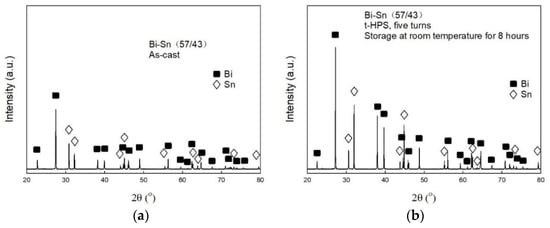
The XRD spectra of a Bi–Sn sample in the as-cast condition and after t-HPS processing for five turns are shown in
Figure 2 where the peaks of pure Bi and Sn are indicated. The XRD pattern reveals that the Bi–Sn (57/43) alloy is composed of pure Bi and pure Sn elements only and no binary compound is detected.
Figure 2. XRD spectrum of the Bi–Sn samples in (a) the as-cast condition and (b) after t-HPS processing for five turns and storage at RT for 8 h.
When the microstructure was observed under a lower magnification, it was noticed that the shear deformation was not homogeneous and there were some narrow dense lamellar bands visible in the matrix. As shown in
Figure 3a, the width of these bands was around 10–20 μm after five turns of t-HPS processing. The phase inside such bands preserved the original lamellar structure of the as-cast sample while the phase structure outside these bands consisted of equiaxed grains. After 20 turns of deformation, the length of dense lamellar bands was much shorter.
Figure 3. Microstructure of the Bi–Sn samples after t-HPS processing for (a) 5 and (b) 20 turns and storage at RT for 8 h, with arrows indicating the lamellar bands.
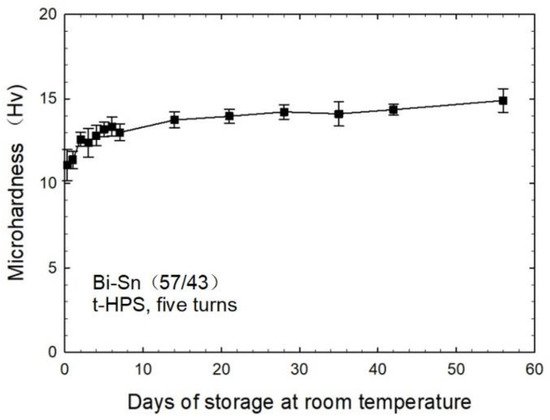
A Bi–Sn sample processed by t-HPS for five turns was used to evaluate the evolution of microhardness during storage at RT. Microhardness indentations were recorded for the sample and these measured values were then plotted against the number of days of storage as shown in
Figure 4. The as-cast Bi–Sn (57/43) alloy had microhardness of ~22.5 ± 0.5 Hv. The microhardness values were recorded as ~11.1 ± 0.9 Hv after t-HPS processing and storage for 8 h at RT. Microhardness increased gradually during storage, reaching ~13.0 ± 0.5 Hv after 7 days of storage, and further increased to ~14.4 ± 0.3 Hv and ~14.9 ± 0.7 Hv after 42 days and 56 days of storage, respectively. Similar behavior was widely reported in low melting temperature materials processed by severe plastic deformation, for example, in the Zn–Al, Sn–Pb and Bi–Sn alloys
[13][14][15][16][17][18][16,17,19,20,21,22]. However, it is worth noting that microhardness of the Bi–Sn (57/43) alloy after t-HPS processing is more stable compared to the condition after processing by HPT. As shown in an earlier study, microhardness of the Bi–Sn alloy dropped from ~25.2 Hv to around 8 Hv after processing by HPT for five turns, and thereafter microhardness increased to around 17 Hv after 7 days of storage at room temperature
[13][14][16,17].
Figure 4. Microhardness of the Bi–Sn samples versus the number of days of storage at RT after t-HPS processing for five turns.
Figure 5 shows the microstructures of the Bi–Sn samples after storage at RT for various periods. The Sn phase was etched away by the etchant so that the Bi phase is clearly visible in the images. As shown in
Figure 5a, the phase structure was broken by the shear stain and there were large numbers of Bi phase islands with essentially equiaxed shape. As the number of storage days increased, the Bi phase grew and connected together again so that the total number of small Bi islands decreased. Moreover, it is observed in all of these images that pitting holes existed inside the Bi phase where these pitting holes had sizes of around several hundred nanometers. It is reasonable to expect that these pitting holes were pre-resolved Sn particles within the Bi phase which were etched away by the etchant.
Figure 5. Microstructures of the Bi–Sn samples after t-HPS processing for five turns and storage at RT for (a) 8 h, (b) 2 days, (c) 7 days and (d) 21 days.
FIB was employed to mill the samples and observe these Sn particles within the Bi phase. The solubility of the second phase was higher in the melted state compared to the solid state, therefore these Sn second-phase particles may participate in solidification and become trapped within the Bi phase. As the material is subjected to t-HPS processing, tips of the large Sn phase may be broken and mixed into the Bi phase through the flow of the materials under shear deformation. This is shown in
Figure 6b where the number of visible Sn particles inside the Bi phase is larger compared to
Figure 6a. Unfortunately, it was not feasible to compare the mean size of these particles as the number of visible particles was not sufficient. It is also observed that the grain boundaries inside each phase were visible after fine milling.
Figure 6. Microstructures (a) of the as-cast Bi–Sn sample and (b) after t-HPS processing for five turns and storage at RT for 8 h.
Tensile tests were conducted on the Bi–Sn samples and the main results of each sample under various initial strain rates are shown in
Table 1. The results demonstrate that the superplasticity of the Bi–Sn alloy was significantly improved by t-HPS processing and elongations to failure of more than 1500% and 1800% were achieved in the sample processed by t-HPS for 5 and 20 turns, respectively. For all the samples, smaller strain rates were favorable for having higher elongations to failure.
Table 1.
Tensile properties of the Bi–Sn samples under various initial strain rates at RT.
| Strain Rate |
1.0 × 10 | −2 | s | −1 |
1.0 × 10 | −3 | s | −1 |
1.0 × 10 | −4 | s | −1 |
| UTS, MPa |
Elongation |
UTS, MPa |
Elongation |
UTS, MPa |
Elongation |
| As-cast |
70 |
~40% |
60 |
~80% |
53 |
~130% |
| 0.25 turns |
69 |
~80% |
48 |
~280% |
33 |
~430% |
| 1 turn |
69 |
~100% |
49 |
~270% |
31 |
~490% |
| 5 turns |
/ |
/ |
42 |
~1170% |
23 |
~1530% |
| 20 turns |
/ |
/ |
26 |
~1060% |
12 |
~1820% |
In this study, an elongation of >1800% was achieved in the Bi–Sn (57/43) sample after t-HPS processing for 20 turns. In an earlier study, a Bi–Sn (58/42) sample processed by HPT for 10 turns featured a superplastic elongation of around 1220% under a strain rate of 1 × 10
−4 s
−1 at RT. Thus, the tensile samples of this study were generally more superplastic and exhibited larger elongations to failure than those processed by HPT
[13][16]. Nevertheless, it should be noted that an elongation of 1900% was achieved in a very early study using larger rod samples of the same alloy after extrusion
[19][18].
3. Principle of tube high-pressure shearing
The principle of t-HPS is depicted schematically in Figure 1 where the sample, in the form of a tube, is radially confined between a central mandrel and an outer cylinder. The principle of the process is that a sufficiently high hydrostatic pressure is introduced in the tube wall so that the frictional forces at the interfaces between the sample-mandrel and the sample-cylinder are high enough to prevent any localized slip. By fixing the mandrel and rotating the outer cylinder (or vice versa), a simple shear strain is then produced in the tube wall.
Figure 1. Schematic illustration of the principles of t-HPS
A critical factor determining the success of t-HPS is to obtain a sufficiently high hydrostatic pressure in the tube wall confined between the central mandrel and the outer cylinder. Different procedures may be adopted for introducing a hydrostatic pressure into the tube wall. A radial force may be applied at the cylinder surface by, for example, compressing the mandrel within the elastic regime. An alternative and attractive procedure is to apply an axial force at the two ends of the tube. This may be accomplished by fully confining the tube through the use of pressure rings at both ends of the sample and then compressing the rings directly to build up a high hydrostatic pressure in the tube wall as illustrated in Figure 1.
The average strain, γ, introduced into the tube wall is:

where Ri and R are the inner and outer radii of the tube respectively.
The strain distribution in fact in tube wall is not uniform and a strain gradient exists. For a constitutional equation in the form where τ0 and A are material constants and n the strain hardening exponent, the shear strain dependence on radical coordinate r is:
where τ0 and A are material constants and n the strain hardening exponent, the shear strain dependence on radical coordinate r is:
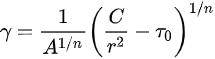
where C is integration constant. This leads to a simpler expression of shear strain γ for the special case of τ0 =0.
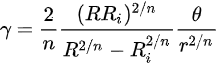
The average equivalent strain:

The equivalent strain distribution for materials with constitutional relation τ = τ0+Aγ n:
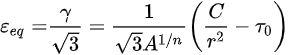
Or for the materials with simple constitutional relation τ = Aγ n:

It is clear that the strain distribution is materials dependent.
It should be noted that edge effect also appears as in other deformation processing [20][21].
t-HPS has been utilized to synthesis multilayered structures in one single step of t-HPS rotation [22].
The following is recent application t-HPS to process eutectic Bi–Sn (57/43) alloy for superplasticity [23].


 where τ0 and A are material constants and n the strain hardening exponent, the shear strain dependence on radical coordinate r is:
where τ0 and A are material constants and n the strain hardening exponent, the shear strain dependence on radical coordinate r is: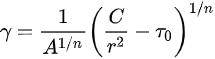
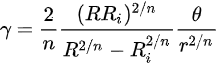

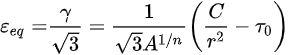







 where τ0 and A are material constants and n the strain hardening exponent, the shear strain dependence on radical coordinate r is:
where τ0 and A are material constants and n the strain hardening exponent, the shear strain dependence on radical coordinate r is: